 |
 |
 |
19.1.1.
Релаксация в сети
Основное назначение
связей в сети зависимостей состоит в том, чтобы, во-первых, показать,
как изменение значения какого-либо параметра распространяется от узла к узлу,
а во-вторых, выявить противоречия между значениями, присвоенными разным узлам.
Пусть, например,
в сети имеются узлы А и М. Узел А представляет ускорение
некоторой детали механизма, а М— массу этой детали. Оба узла, А и
М, содействуют узлу F, который представляет силу, действующую
на деталь. Более того, учитывая знакомую всем со школьной скамьи формулу f=
та, узлы А и М также и принуждают узел F, поскольку
если а и т известны, то значение f определяется этой формулой
и не может быть произвольным, т.е. если а - 2 и от = 3, то мы
можем присвоить узлу F только значение f= 6. Если же этому узлу
уже ранее было присвоено значение f= 7, то сеть переходит в состояние противоречия.
Формула f=
та играет роль принудительного ограничения для сети, описанной в этом примере.
Если все ограничения в сети удовлетворяются, то она пребывает в состоянии
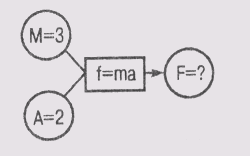
релаксации. Рассмотрим варианты сетей, представленные на рис. 19.1. Сеть
а) находится в промежуточном состоянии, поскольку узлу F не присвоено
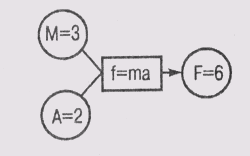
какого-либо определенного значения, сеть б) находится в состоянии релаксации,
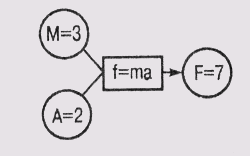
а сеть в) — в состоянии противоречия.
Строго говоря,
термин "релаксация" относится к сети, а не к теории13.
Но сеть есть не что иное, как только представление определенной теории, например
сеть а) является представлением теории
f= mа
т=3
а
= 2,
в которой
формула f= та играет роль принудительного ограничения. Сеть б) представляет
теорию
f= mа
т=3
а = 2
f=6,
которая находится
в состоянии релаксации по отношению к ограничению f= та, а сеть в) представляет
противоречивую теорию
f=
mа
т=-3
а = 2
f=7.
По ходу изложения,
не оговаривая отдельно, мы будем "перескакивать" от сетей к теориям,
а для простоты использовать термин "представление", если нежелательно
подчеркивать различие между этими двумя способами-реализации фактов и ограничений.
а
б
с
Рис. 19.1. Сети зависимостей с принудительными ограничениями. Окружностями представлены узлы сети, а прямоугольниками — связи
 |
 |
 |
