|
1. Вектором называется направленный отрезок. Длина соответствующего отрезка
называется модулем вектора. Модуль вектора
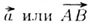
обозначается а или АВ (пишут также 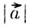 , ,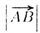 ).
).
Векторы, расположенные на одной прямой пли па параллельных прямых, называются
коллинеарными. Два вектора называются равными, если они коллинеарны, имеют
одинаковые направления и одинаковые модули.
Вектор называется нулевым, если его модуль равен 0.
2. Линейными называются действия сложения, вычитания векторов и умножения
вектора на число.
Геометрическое определение и выполнение линейных действии (рис. 20):

a) Сумма  . Если начало . Если начало 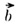 совмещено
с концом совмещено
с концом  , то начало , то начало  совпадает с началом
совпадает с началом  , а конец
— с , а конец
— с
концом 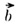 . .
Или, если начала  и и 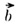 совмещены, то
совмещены, то  — диагональ параллелограмма
со сторонами а и b , идущая из общего начала — диагональ параллелограмма
со сторонами а и b , идущая из общего начала  и
и 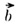 . .
b) Разность  - - 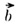 . Если начала векторов
. Если начала векторов  и и 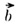 совмещены, то начало
совмещены, то начало  - - 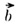 совпадает с концом
совпадает с концом 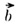 , а конец , а конец
 - - 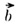 совпадает с концом
совпадает с концом  . .

3. Запись
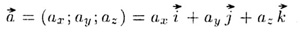
обозначает, что вектор  имеет
координаты ax,
аy,
аz
или имеет
координаты ax,
аy,
аz
или  разложен по базису разложен по базису
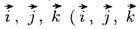 — орты осей Ох. Оу и Oz пространственной
системы координат Оx;Oy;
Oz.
При этом — орты осей Ох. Оу и Oz пространственной
системы координат Оx;Oy;
Oz.
При этом

4. Линейные действия над векторами распространяются на их координаты:

5. Скалярное произведении двух ненулевых векторов  и
и 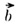 - это число, определяемое
одним из следующих равенств: - это число, определяемое
одним из следующих равенств:

где
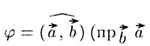
— проекция вектора  на вектор на вектор
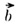 ). Если хотя бы один из векторов
а и b является пулевым вектором, то ). Если хотя бы один из векторов
а и b является пулевым вектором, то  •
• 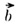 = 0. При этом: = 0. При этом:
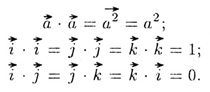
Условие перпендикулярности  и
и 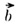 : :
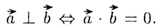
|