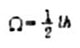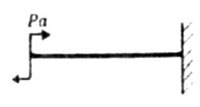начало раздела: Шпаргалки
 |
||||||||||||||||||||
| ПРАВИЛО ВЕРЕЩАГИНА | ||||||||||||||||||||
При вычислении интегралов вместо аналитических выражений
моментов используются их эпюры. Т.е. значение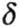 
можно найти по способу Верещагина, "перемножив" эпюры Мp
и М1. |
||||||||||||||||||||
| "Перемножить" две эпюры - значит площадь нелинейной эпюры изгибающих моментов умножить на ординату другой обязательно линейной эпюры, находящейся под центром тяжести первой, и результат разделить на жесткость (в случаях, когда на данном участке обе эпюры линейны, совершенно безразлично, на какой из них брать площадь, а на какой ординату). | ||||||||||||||||||||
 |
||||||||||||||||||||
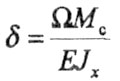где  - площадь
произвольной фигуры; |
||||||||||||||||||||
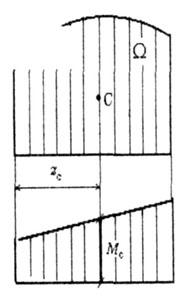
| Мc
- ордината прямолинейной эпюры, соответствующей центру тяжести площади
(рис. 6.2). |
||||||||||||||||||||
 |
||||||||||||||||||||
| Рис. 6.2 | ||||||||||||||||||||
 |
||||||||||||||||||||
| Рис. 6.3 | ||||||||||||||||||||
Произведение 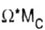 в
пределах рассматриваемого участка положительно, если площадь 
и соответствующая ордината Мc
расположены по одну сторону от оси данного участка, и отрицательно, если
они расположены по разные стороны. |
||||||||||||||||||||
| В тех случаях, когда эпюра является сложной, для определения ее площади или координаты центра тяжести эпюру разбивают на простейшие фигуры (рис. 6.3), для которых легко определить площадь и положение центра тяжести. | ||||||||||||||||||||
| Таким образом, при определении перемещений с использованием правила Верещагина, соблюдают следующую последовательность: | ||||||||||||||||||||
|
||||||||||||||||||||
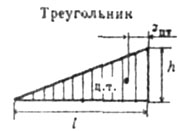
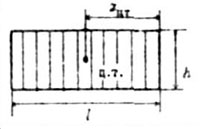
| Ниже приведены величины площадей фигур и координат центров тяжести простейших эпюр (табл.1). | ||||||||||||||||||||
| Таблица 1. | ||||||||||||||||||||
| начало раздела: Шпаргалки
|
||||||||||||||||||||
|
