
|

|

|
Пример с матрицей МКР
Для начала рассмотрим пример использования valarray л его сечения в задаче, более близкой к жизни, чем все другие учебные примеры, приводившиеся ранее. Когда-то вы слышали о том, что электронные вычислительные машины (ЭВМ) изобрели для того, чтобы решать дифференциальные уравнения. Не удивлюсь, узнав, что существуют успешно зарабатывающие на жизнь программированием молодые люди, которые об этом не знают. Однако это правда. Рассмотрим npot стое уравнение, которое способно довольно сносно описать многие процессы и явления нашей жизни j
d/dx(p*(dU/dx))+kU=-f
Это уравнение Пуассона и оно, например, (при k = 0 и f = 0) способно описать стационарное тепловое поле в самом простом одномерном случае, когда температура U = U(x) почему-то зависит только от одной координаты х. Например, в длинном неоднородном стержне, теплоизолированном с боков. Символ р в этом случае имеет смысл коэффициента теплопроводности материала стержня, который в принципе может зависеть от координаты р = р(х), а символ f = f(x) имеет смысл точечного источника тепла. Если f тождественно равна нулю, то мы имеем частный случай — уравнение Лапласа. Источником теплового поля в этом случае является известная температура или скорость ее изменения на границах расчетной области. Отсюда происходит термин краевая задача, то есть задача, в которой заданы граничные условия (условия на краях расчетной области). В задачах такого рода требуется найти все значения температуры внутри области. Областью расчета в одномерном случае является отрезок прямой линии. Например, слева жарко, а справа холодно. Спрашивается, а как распределена температура внутри отрезка?
Считается,
что в макромире температура распределена непрерывно, то есть в каждой точке,
число которых не поддается счету, она имеет свое собственное значение. При попытке
решить задачу на компьютере (сугубо дискретной структуре) надо отказаться от
идеи бесконечности и ограничиться каким-то разумным числом точек, например N
= 300. По опыту знаю, что график из трехсот точек вполне прилично выглядит на
экране. Приняв это решение, разбивают всю область 300 точками на 299 отрезков
и заменяют (аппроксимируют) производные дифференциального уравнения конечными
разностями. Такова основная идея метода конечных разностей (МКР). При этом одно
дифференциальное уравнение заменяется 298 алгебраическими уравнениями по числу
внутренних точек, так как две граничные точки не требуют аппроксимации. Вот
мы и пришли к необходимости решать систему алгебраических уравнений из 298 уравнений
с 298 неизвестными температурами во внутренних точках расчетной области.
Примечание
Точно такое же уравнение описывает и многие другие физические явления. Изменяется лишь смысл параметров р и k. Например, магнитное поле в центральном поперечном сечении электрической машины с некоторыми незначительными поправками, вызванными переходом к цилиндрической системе координат, тоже с успехом может быть описано подобным уравнением.
Для того чтобы
поместить матрицу системы алгебраических уравнений в последовательность типа
valarray и начать орудовать его сечениями (slice), надо сначала немного потрудиться
и хотя бы понять структуру матрицы. Затем следует выработать алгоритм вычисления
ее коэффициентов, и только после этого использовать динамические структуры данных
и алгоритмы STL для решения задачи.
Тем, кто почувствовал
себя неуютно в незнакомой обстановке, скажем, что это нетрудно и даже интересно.
Поэтому не торопитесь отбросить книгу, а продолжайте чтение и, может быть, вы
еще завоюете мир, разработав великолепный инструмент для решения краевых задач
в трехмерной постановке. Для начала рассмотрите схему расчетной области, которая
приведена на рис. 11.1.
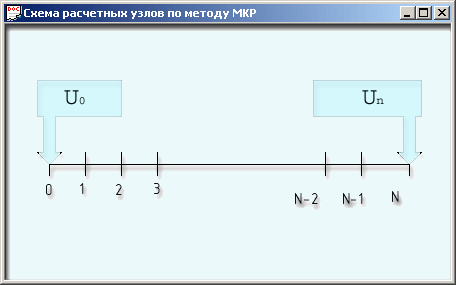
Рис. 11.1.
Схема расчетных узлов по методу МКР
Напомним, что
нашей задачей является найти значения температуры или любой другой функции U
во всем множестве точек М = {1, 2, ..., N-2, N-1}, считая, что в двух точках
{О, N} она известна. Переход к конечным разностям производится с помощью трехточечного
шаблона, который изображен на рис. 11.2.
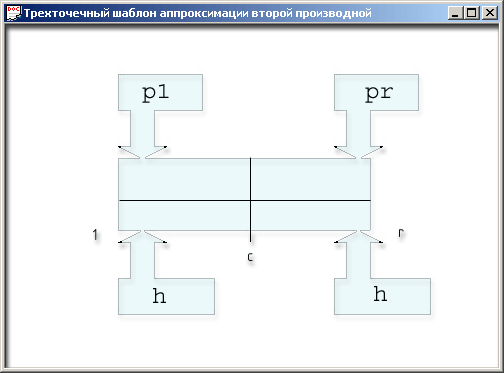
Рис. 11.2.
Трехточечный шаблон аппроксимации второй производной
Мы имеем три
точки и два отрезка, которых вполне достаточно, чтобы справиться со второй производной
при попытке ее приближенного вычисления. Индексы 1, г и с означают left, right
и center. Обозначение pi принято для коэффициента, учитывающего свойства среды
левого отрезка, например теплопроводности, а рг — правого. Шаги разбиения области
вдоль оси х считаются одинаковыми и равными h. Теперь вы должны представить
себе, что центр этого шаблона по очереди приставляется ко всем точкам из множества
М. В результате этой процедуры мы по одному будем получать все |М| = N - 1 алгебраических
уравнений, приближенно заменяющих одно дифференциальное уравнение Пуассона,
которое, как говорят физики, удовлетворяется во всех точках этой части реального
пространства.
Возвращаясь
к шаблону из трех точек, напомним, что производная по х — это в некотором роде
степень изменения функции, то есть скорость ее роста или падения вдоль этой
координаты. Приближенно она равна:
dU/dx=(Ur-Uc)/h
для правого
отрезка и
dU/dx=(Uc-U
l
)/h
для левого.
Теперь надо записать приближенную оценку для второй производной с учетом коэффициента
теплопроводности. Он может иметь разные значения (р! и рг) в левой и в правой
частях шаблона:
d
/dx(pdU/dx)={(pr[Ur-Uc])/h-(pl[Uc-Ul])/h
}/h
(2)
Произведя подстановку
в исходное дифференциальное уравнение (1) и упростив выражение, получим алгебраическое
уравнение:
aU
l+bU
c
+cU
r
=0
(3)
связывающее
температуры трех соседних узлов сетки с физическими свойствами прилежащих участков
пространства, так как значения коэффициентов уравнения зависят от р, k и h:
a=pl/h^2;
c=pr/h^2; b=-a-c+k;
(4)
Коэффициент
а
описывает свойства левой части шаблона, а
с —
правой, а
Ь
—
обеих вместе. Чуть позже мы увидим, что коэффициент
b
попадет в
диагональ матрицы. Теперь надо примерить шаблон ко всем узлам сетки. Узел номер
1 даст уравнение:
a 1 U 0 +b 1 U 1 +c 1 U 2 =0,
узел номер
2:
a
2
U
1
+b
2
U
2
+c
2
U
3
=0,
и т. д. Здесь
важно следить за индексами. Для простоты пока считаем, что коэффициенты а,,
b,, с,
не изменяются при переходе от узла к узлу. В узлах сетки вблизи
границ (то есть в узле 1 и узле N-1) уравнения упрощаются, так как £/„
и
U
N
считаются известными и поэтому перемещаются в правую
часть уравнения. Так, первое уравнение системы станет:
b 1 U 1 +c 1 U 2 =0,
а последнее:
a
n-1
U
n-2
+b
n-1
U
n=+1
=0,
Все остальные
уравнения будут иметь вид (3). Теперь пора изобразить всю систему уравнений,
используя матричные обозначения и не отображая многочисленные нули. Для простоты
будем считать, что N = 5:
| b 1 | c1 | U1 | -a1U0 | |||
| a2 | b2 | c2 | U2 | 0 | ||
| a3 | b3 | c3 | U3 | = | 0 | |
| a4 | b4 | U4 | -c4U5 |
Вы видите,
что матрица системы уравнений имеет характерную регулярную трех-диагональную
структуру, а структура вектора правых частей тоже легко прочитывается. Граничные;
условия краевой задачи заняли подобающие им крайние места, а внутренние позиции
— нули.
Решать такую
систему следует специальным методом, который называется методом прогонки и является
модификацией метода Гаусса. Он работает во много раз быстрее самого метода Гаусса.
Мы реализуем его немного позже, а сейчас попробуем применить алгоритм generate
из библиотеки STL для генерации матрицы, имеющей рассмотренную структуру, и
вектора решений U. В простых случаях он известен и легко угадывается. Затем
с помощью сечений произведем умножение Матрицы на вектор и убедимся в том, что
вектор правых частей системы уравнений будет иметь правильную структуру и значения.
Эту часть работы рассматривайте как дополнительное упражнение по использованию
структур данных типа valarray и slice. В процессе решения краевой задачи мы
будем пользоваться контейнерами другого типа (vector), так как метод прогонки
не требует применения каких-то особых приемов работы с сечениями.
Если для простоты
принять р = 1, h = 1, U
0
= 100, a
U
N
=0, то коэффициенты
матрицы будут равны a
i
= с
i
= 1, b
i
. = -2 ,
k = 0, а решение U(x) известно заранее. Это — линейно спадающая от 100 до 0
функция, а в более общем случае — функция произвольных граничных условий:
U(x)=U
0
+[U
n
-U
0
]x/L
где L — длина всей расчетной области. Правильность решения проверяется прямой подстановкой в уравнение (1).

|

|

|
