Решение неравенств. Метод интервалов

Целесообразно описать волну знаков стандартной рациональной функции и применение ее к методу интервалов. Рациональную функцию

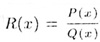
назовем стандартной, если ее числитель Р(х) и знаменатель Q(x) разложены на простые (быть может, кратные) множители, причем старшие коэффициенты всех множителей — положительны.

Волна знаков — удобное средство интерпретации (закрепления) интервалов зпакопостояистца функции R(х). Ке чертят справа налево, начиная ее над осью Ох и проводят через все корни Р(х) и Q(x). При этом:

если кратность какого-либо корня почетная, то волна пересекает ось Оx, т. е. переходит с одной стороны оси Оx на другую;

если кратность какою-либо корня четная, то волна остается но одну сторону оси Ох (такую точку, корень, назовем точкой возврата).

Методом интервалов удобно решать рациональные неравенства, в том числе и целые, т.е. неравенства вида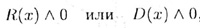

, где D(х) — многочлен, а знак /\ — один из знаков неравенства «>». «

», «<», «

».

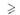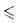При строгом неравенстве ответ состоит только из интервалов.

При нестрогом неравенстве в ответ включают также корни только числителя и отдельные точки — точки возврата, соответствующие корням числителя.

Blog