Задачи на составление уравнений. Прогрессии

• Как правило, основная трудность при решении текстовой задачи состоит в переводе ее условий на математический язык уравнений. Общего "способа такого перевода не существует. Однако многие задачи, встречающиеся на вступительных экзаменах, достаточно типичны.

Начнем с задач на проценты. Эта тема стала весьма популярной в текстовых задачах вступительных экзаменов в последние годы. При решении таких задач полезно помнить следующее:

1) процент величины — одна сотая часть этой величины;

2) если число а составляет р% от числа b, то эти числа связаны равенством

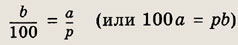
3) если число а увеличено на р%, то оно увеличено в

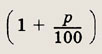
раз, а если уменьшено на q%, где

то оно уменьшено в

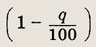
раз. При этом соответственно получаются числа

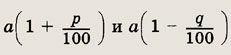
Задание 1.

Выработка продукции предприятием за 1997 год увеличилась на 20%, а за 1998 год—еще на 10%. На сколько процентов увеличилась выработка продукции за два года?

Решение:

Пусть S — количество продукции, выработанное предприятием за 1996 год. Тогда

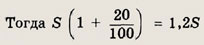
— количество продукции, произведенное предприятием за 1997 год;

— количество продукции, произведенное предприятием за 1998 год. За два года выработка увеличилась в 1,32 раза, т. е. на 32% .

Ответ:

на 32%

Задание 2.

Себестоимость продукции сначала повысилась на 20%, а затем понизилась на 10%. На сколько процентов изменилась себестоимость продукции?

Ответ:

Повысилась на 8%

Задание 3.

Цена на товар была повышена на 25% . На сколько процентов теперь ее надо снизить, чтобы получить первоначальную цену товара?

Ответ:

20%

Задание 4.

Первоначальную цену товара снизили на 10%, затем еще на 20% . После этого цену снова снизили на 25%. На сколько процентов всего снизили цену товара?

Ответ:

46%

Задание 5.

Количество студентов в институте, увеличиваясь на одно и то же число процентов ежегодно, за три года возросло с 5000 до 6655 человек. На сколько процентов ежегодно увеличивалось число студентов?

Ответ:

10%

Задание 6.

За некоторый период времени количество акций у гражданина Иванова увеличилось на 30%. На сколько процентов увеличилась общая стоимость акций гражданина Иванова, если цена каждой акции увеличилась на 20% ?

Ответ:

56%

Задание 7.

За некоторый период времени количество акций гражданина Петрова увеличилось на 17%. На сколько процентов увеличилась цена каждой акции, если общая стоимость его акций увеличилась на 134%?

Решение:

Пусть: р — процент увеличения стоимости одной акции; TV — первоначальное число акций; х — первоначальная цена одной акции.

Тогда: NX— первоначальная стоимость всех акций; 1,17N — новое число акций;

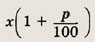
— новая цена одной акции;

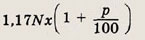
— новая стоимость всех акций.

По условию:

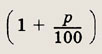
Отсюда р = 100%.

Ответ:

100%.

Задание 8.

Магазин продал книгу со скидкой в 10% по сравнению с первоначально названной ценой и получил при этом 8% прибыли. Сколько процентов прибыли предполагал получить магазин первоначально?

Ответ:

20%

Задание 9.

Магазин продал товар со скидкой в 20% по сравнению с первоначально названной ценой и понес при этом 4% убытка. Сколько процентов прибыли предполагал получить магазин первоначально?

Решение:

Пусть: х — первоначально названная цена; у — оптовая цена, т. е. цена товара, по которой ее приобрел магазин.

Тогда по условию: 0,8х = 0,96у, откуда х = 1,2у, т. е. х составляет 120% от у. Следовательно, магазин предполагал получить 20% прибыли.

Ответ:

20%.

Задание 10.

Собрали 42 кг свежих грибов, содержащих 95% воды по массе. Когда их подсушили, они стали весить 3 кг. Каков процент содержания воды по массе в сухих грибах?

Ответ:

30%

Задание 11.

Свежие грибы содержат по массе 90% воды, а сухие — 20%. Сколько (по массе) надо собрать свежих грибов, чтобы из них получить 4,5 кг сухих грибов?

Ответ:

36 кг.

Задание 12.

Зарплата некоторой категории служащих повышалась дважды, причем процент повышения зарплаты во второй раз был вдвое больше, чем в первый. На сколько процентов была повышена зарплата в первый раз, если до первого повышения она была равна 700 р., а после второго повышения составила 924 р.?

Ответ:

10%

Задание 13.

Выработка продукции за год работы предприятия возросла на р% , а за следующий год она возросла на 10% больше, чем за предыдущий. На сколько процентов увеличилась выработка продукции за первый год, если за два года она увеличилась в общей сложности на 48,59% ?

Решение:

Пусть S — количество продукции, выработанное предприятием за предыдущий год. Тогда для искомой величины р имеем следующее уравнение:

Сокращая на S и приводя дроби к общему знаменателю, получим

(р + 100)(р + 110) = 14859, р²+ 210р - 3859 = 0

Решив это уравнение, находим р = 17.

Ответ:

17%

Задание 14.

В результате переоборудования цехов производительность завода за год работы увеличилась на р%. На следующий год в результате улучшения системы управления — еще на (р + 50)%. На сколько процентов увеличилась производительность завода за первый год, если за два года она возросла в общей сложности втрое?

Ответ:

50%

Задание 15.

В начале года на сберкнижку было положено 1640 р., а в конце года после начисления процентов, взято обратно 882 р. Еще через год на сберкнижке снова оказалось 882 р. Сколько процентов начисляет Сбербанк в год?

Решение:

Пусть р — процент начисления по вкладу Сбербанком за год. Тогда к началу второго года на сберкнижке оставалось

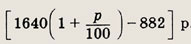
За второй год на эту сумму снова начислено р% годовых. Получаем уравнение

Положим

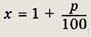
Тогда 1640х² - 882х - 882 = 0. Решив это уравнение, находим х = 1,05.

Таким образом, р = 5%.

Ответ:

5%

Задание 16.

Население города в начале первого года составляло 150 000 человек. В конце года из других мест в город прибыло 12 000 человек. В результате естественного прироста и вновь прибывших, в конце второго года население города составило 171 495 человек. Определите процент естественного прироста населения за год.

Ответ:

3%

Задание 17.

Два банка выплачивают доход по вкладам 16% и 20% годовых соответственно. Сколько денег положил вкладчик в каждый банк, если известно, что первоначальный общий вклад был равен 800 р., а спустя год он увеличился на 136 р.?

Ответ:

600 р. и 200 р.

Задание 18.

Торговая фирма получила две партии товара. Если продавать весь товар по цене 360 р. за 1 кг, то выручка от продажи будет на 20% ниже той, которую фирма получила бы, продав первую партию товара по названной цене, а вторую — по цене, превышающей ее на 30%. Какую часть (по массе) составляет первая партия товара в общем количестве товара этих двух партий?

Ответ:

Задание 19.

В магазин завезли две партии товара и продали его по единой цене за 1 кг. Если бы товар первой партии продавали дешевле на 10% за 1 кг, а товар второй партии дороже на 20% за 1 кг, то общая выручка была бы выше полученной на 10%. Какую часть (по массе) составляет первая партия товара в общем количестве товара этих двух партий?

Решение:

Пусть: х, у — масса товара первой и второй партии соответственно; z — цена, по которой товар был продан. Из условия следует равенство

(х + y)z • 1,1 = хz • 0,9 + уz • 1,2

откуда 0,2х = 0,1у, т. е. у = 2х. В задаче требуется найти отношение

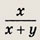
Получаем

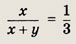
Ответ:

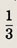
Задание 20.

Скорость автомобиля на шоссе на 12,5% больше скорости по грунтовой дороге, а время, за которое он проехал расстояние по грунтовой дороге, на 10% меньше, чем на шоссе. На сколько процентов расстояние по шоссе больше расстояния по грунтовой дороге?

Ответ:

25%

Задание 21.

На фирме работает 50 человек. При этом 37 из них владеют акциями компании А, а 43 — акциями компании B. Сколько человек (в процентах) владеет акциями обеих компаний, если каждый работник фирмы является владельцем хотя бы одной акции?

Решение:

Число пакетов акций, которыми владеют 50 сотрудников фирмы, равно 37 + 43 = 80. Следовательно, 30 человек владеют акциями обеих компаний, что составляет 60% сотрудников фирмы.

Ответ:

60%

Задание 22.

В школе 120 старшеклассников. Известно, что 78 из них играют в баскетбол, а 72 — в теннис. Какая часть старшеклассников (в процентах) играет и в баскетбол, и в теннис, если каждый из них занимается хотя бы одной из этих игр?

Ответ:

25%

Задание 23.

Известно, что 26 сотрудников некоторой фирмы владеют акциями компании А, а 31 — акциями компании В. При этом 14% всех сотрудников фирмы владеет акциями обеих компаний. Сколько человек работает на фирме, если каждый сотрудник является обладателем хотя бы одной акции?

Решение:

Пусть n —число сотрудников данной фирмы, тогда (26 + 31) - n — число сотрудников, владеющих акциями компаний А и В. По условию (57 - n) составляет 14% от n. Получаем равенство 57 - n = 0,14л, откуда n = 50.

Ответ:

50 человек

Задание 24.

Известно, что 18 сотрудников некоторой фирмы владеют акциями строительной компании, а 24 — акциями компании по производству моющих средств. При этом 40% сотрудников фирмы владеют акциями обеих компаний. Сколько человек работает на фирме, если каждый сотрудник является обладателем хотя бы одной акции?

Ответ:

30 человек

Задание 25.

Суммарный доход двух фирм возрастет на 100% , если доход первой фирмы увеличится в 3 раза, а доход второй фирмы останется неизменным. На сколько процентов надо увеличить доход второй фирмы, оставляя первоначальным доход первой, чтобы их суммарный доход возрос в 3 раза?

Ответ:

400%

Задание 26.

Банк запланировал провести торги в августе и сентябре. Если объем торгов в августе увеличить в 5 раз, а в сентябре оставить на запланированном уровне, то суммарный объем торгов возрастет на 300% . Во сколько раз нужно увеличить план торгов на сентябрь, оставив неизменным план на август, чтобы суммарный объем торгов за два месяца вырос на 400% ?

Ответ:

в 17 раз

Задание 27.

Число приватизированных квартир в доме составляет от 4,3% до 5,8% от общего числа квартир. Каково минимально возможное число квартир в таком доме?

Решение:

Пусть n — число квартир в доме, т — число приватизированных квартир. Тогда по условию

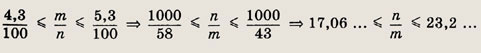
Таким образом, дробь

где n и m — натуральные числа, заключена между двумя положительными числами. Числитель дроби будет минимальным при минимально возможном знаменателе. Взяв m = 1, получаем n = 18.

Ответ:

18 квартир

Задание 28.

Число приватизированных квартир в доме заключено в пределах от 96,5% до 97,2% от общего числа квартир. Каково минимально возможное число квартир в таком доме?

Ответ:

29 квартир

Задание 29.

Установлено, что на дискете число файлов, зараженных вирусом, находится в пределах от 3,89% до 4,44% от общего числа файлов на этой дискете. Чему равно минимально возможное число незараженных файлов на этой дискете?

Ответ:

23 файла

Задание 30.

На сберегательный счет, который вкладчик имел в начале первого года, банк начислил в конце этого года р%, а на тот счет, который вкладчик имеет в начале второго года, начисляется в конце этого года p %, причем р + q = 70. Вкладчик положил на счет в начале первого года некоторую сумму и снял в конце того же года (после начисления процентов) половину положенной суммы. При каком значении q сберегательный счет вкладчика в конце второго года окажется максимально возможным?

Ответ:

10%

Задание 31.

На сберегательный счет, который вкладчик имел в начале первого года, банк начисляет в конце этого года р%, а на тот счет, который вкладчик имеет в начале второго года, начисляется в конце этого года r%, причем р + r = 140. Вкладчик положил на счет в начале первого года некоторую сумму и снял со счета в конце того же года (после начисления процентов) пятую часть положенной суммы. При каком р сберегательный счет вкладчика в конце второго года окажется максимально возможным?

Решение:

Если N — первоначальная сумма вклада, то к началу второго года эта сумма составит

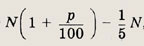
а к концу второго года (после начисления процентов по вкладу) эта сумма у(р) запишется следующим образом:

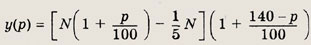
т. е.

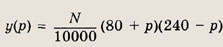
Таким образом, у(р) представляет собой квадратный трехчлен относительно переменной р. Его корни p₁ = -80, р₂ = 240, коэффициент при старшем члене

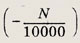
Значит, наибольшее значение у(р) достигается при

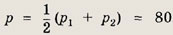
Ответ:

80%

Задание 32.

Банк планирует на один год вложить 30% имеющихся у него средств клиентов в проект А, а остальные 70% — в проект В. В зависимости от обстоятельств проект А может принести прибыль в размере от 32% до 37% годовых, а проект В — от 22% до 27% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им процент от дохода по заранее установленной ставке, уровень которой должен находиться от 10% до 20% годовых. Определите, какую наименьшую и наибольшую чистую прибыль в процентах годовых от суммарных вложений в проекты А и В может при этом получить банк.

Ответ:

5% и 20%

Задание 33.

Банк планирует вложить на один год 40% имеющихся у него средств клиентов в проект X, а остальные 60% — в проект Y. В зависимости от обстоятельств проект X может принести прибыль в размере от 19% до 24% годовых, а проект Y — от 29% до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определите наименьший и наибольший возможный уровень процентной ставки по вкладам, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты X и Y.

Решение:

Найдем наименьший и наибольший доходы от вложений в проекты X и Y. Пусть N — сумма вложений; тогда:

1) 0,4/V • 1,19 + 0,6/V • 1,29 - N = 0,257N — наименьший доход (мы сложили наименьшие доходы по каждому проекту и вычли первоначально вложенную сумму);

2) 0,4 N • 1,24 + 0,6/V • 34 - N = 0,37N — наибольший доход (сложили наибольшие доходы по каждому проекту и снова вычли первоначально вложенную сумму).

Наименьший возможный уровень процентной ставки по вкладам:

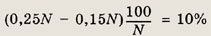
(банк из наименьшего дохода забрал наиболыную запланированную чистую прибыль 0,157N).

Наибольший возможный уровень процентной ставки по вкладам:

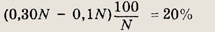
(банк из наибольшего дохода забрал наименьшую запланированную чистую прибыль 0,1N).

Ответ:

10% и 20%

 

• К рассмотренным задачам на проценты тесно примыкают задачи на сплавы, растворы и смеси. Напомним, что если а (кг) некоторого вещества содержится в b (кг) смеси (сплава, раствора), то процентное содержание р (или процентная концентрация) этого вещества в этой смеси находится по формуле

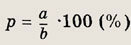
Задание 34.

Кусок сплава меди и цинка массой 36 кг содержит 45% меди. Какую массу меди следует добавить к этому куску, чтобы получить сплав, содержащий 60% меди?

Ответ:

13,5 кг.

Задание 35.

К раствору, который содержит 40 г соли, добавили 200 г воды, после чего концентрация раствора изменилась на 10% . Сколько воды содержал раствор?

Решение:

Пусть исходный раствор содержал х (г) воды. Тогда концентрация исходного раствора равна

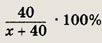
После добавления 200 г воды концентрация нового раствора стала равной

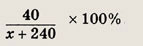
По условию,

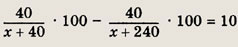
Решив это уравнение, получаем х = 160 г.

Ответ:

160 г.

Задание 36.

Сколько воды нужно выпарить из 500 кг целлюлозной массы, содержащей 90% воды, чтобы получить массу с содержанием воды 50% ?

Ответ:

400 кг.

Задание 37.

Имеются два куска сплава серебра с медью. Один из них содержит 81% меди, другой — 95% . В каком отношении по массе нужно брать сплавы от обоих кусков, чтобы получить новый сплав, содержащий 87% меди?

Ответ:

4 : 3

Задание 38.

Имеются два сплава золота с серебром. В первом сплаве количество этих металлов находится в отношении 1 : 2, во втором — 2:3. Сколько граммов первого сплава нужно взять, чтобы получить 19 г сплава, в котором золото и серебро находятся в отношении 7 : 12?

Ответ:

9 г.

Задание 39.

Имеются два разных сплава меди со свинцом. Если взять 1 кг первого сплава и 1 кг второго сплава и переплавить их, то получится сплав, содержащий 65% меди. Известно, что при переплавке обоих сплавов, имеющих суммарную массу 7 кг, получается сплав, содержащий 60% меди. Сколько меди будет содержать сплав, получающийся при переплавке куска первого сплава, равного по массе куску второго сплава, и куска второго сплава, равного по массе куску первого сплава? Ответ запишите в процентах.

Решение:

Пусть х (кг) — масса первого сплава, (7 - х) (кг) — масса второго сплава; р% и q% — процентные содержания меди в первом и втором сплавах. Тогда по условию

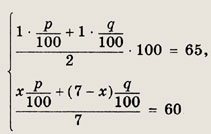
При этом требуется найти величину

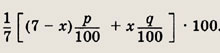
Упрощая записанные уравнения, имеем

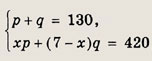
а нужно найти

Умножая первое уравнение в системе на 7 и вычитая из результата второе, получаем

(7 - х)р + хq = 490,

т. е. искомая величина равна 70% (или 4,9 кг).

Ответ:

70%

Задание 40.

Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй — 26% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Сплавив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько олова (по массе) содержится в получившемся сплаве?

Ответ:

170кг

Задание 41.

Имеются три сплава. Первый содержит 45% олова и 55% свинца, второй — 10% висмута, 40% олова и 50% свинца, третий — 30% висмута и 70% свинца. Из них нужно получить сплав, содержащий 15% висмута и 60% свинца общей массой 10 кг. Сколько килограммов каждого сплава нужно взять?

Для удобства запишем данные в таблицу:

	Висмут	Олово	Свинец	Масса (кг)
I сплав	0%	45%	55%	х
II сплав	10%	40%	50%	у
III сплав	30%	0%	70%	z

Определив нужные концентрации сплавов и учитывая, что х + у + z = 10, приходим к системе уравнений

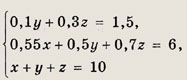
Из первого уравнения получаем у = 15 - 3z, а из третьего х = 2z - 5. Подставляя эти выражения во второе уравнение системы, имеем 3z = 12,5. Отсюда

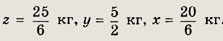
Ответ:

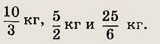
Задание 42.

Имеются три куска сплава меди с никелем в отношениях 2:1,3:1и5:1по массе. Из них сплавлен кусок массой 12 кг с отношением содержания меди и никеля 4:1. Найдите массу каждого исходного куска, если масса первого из них вдвое больше массы второго.

Ответ:

1,92; 0,96; 9,12 кг.

Задание 43.

Сплав состоит из олова, меди и цинка. Если от этого сплава отделить 20 г и сплавить с 2 г олова, то во вновь получившемся сплаве масса меди будет равна массе олова. Если же отделить от первоначального сплава 30 г и сплавить с 9 г цинка, то в этом новом сплаве масса олова будет равна массе цинка. Определите (в процентах) состав первоначального сплава.

Ответ:

40%; 50% ; 10%

Задание 44.

Из колбы, в которой содержится 80 г 10%-ного раствора поваренной соли, отливают некоторую часть раствора в пробирку и выпаривают до тех пор, пока процентное содержание соли в пробирке не повысится втрое. После этого выпаренный раствор выливают обратно в колбу. В результате содержание соли в колбе повышается на 2% . Сколько граммов раствора отлили из колбы в пробирку?

Ответ:

20 г.

Задание 45.

В лаборатории имеются растворы поваренной соли четырех различных концентраций. Если смешать первый, второй и третий растворы в весовом отношении 3 : 2 : 1, то получится 15%-ный раствор. Второй, третий и четвертый растворы, взятые в равной пропорции, дают при смешении 24%-ный раствор, а раствор, составленный из равных по массе частей первого и третьего растворов, имеет концентрацию 10% . Какая концентрация получится при смешении второго и четвертого растворов в пропорции 2:1?

Ответ:

29 %

Задание 46.

Из сосуда, содержащего чистый спирт, отлили 1/3 часть и добавили такое же количество воды. Затем отделили 1/3 часть смеси и снова добавили такое же количество воды. Такую операцию проделали k раз. При каком наименьшем k процентное содержание спирта в сосуде станет менее 10% ?

Ответ:

6

Задание 47.

Из сосуда, содержащего чистую воду, отлили 1/5 часть и добавили такое же количество чистого спирта. Затем отлили 1/5 часть смеси и снова добавили такое же количество чистого спирта. Такую операцию проделали n раз. При каком наименьшем п процентное содержание спирта в сосуде станет больше 80%?

Решение:

Пусть объем сосуда равен 1 л. Найдем объем чистого спирта в сосуде на каждом шаге. Имеем:

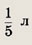
на 1-м шаге;

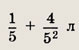
на 2-м шаге;

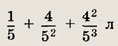
на 3-м и т. д. На n-м шаге получаем, что в сосуде

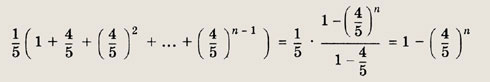
литров чистого спирта. Следовательно, нужно указать минимальное целое п, при котором

Последнее неравенство можно записать в виде (1,25)ⁿ > 5, откуда n = 8.

Ответ:

8

Задание 48.

Имеются два сосуда с растворами поваренной соли: в первом сосуде 3 кг 10% -ного по массе раствора, а во втором 2 кг 20%-ного раствора. Из первого сосуда выпаривают некоторое количество воды, а затем все содержимое второго сосуда переливают в первый. Какое количество воды нужно выпарить, чтобы после переливания в первом сосуде получился r% -ный раствор соли? Найдите все r, при которых задача имеет решения.

Ответ:

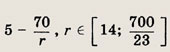
Задание 49.

В сосуд вместимостью 6л налито 4л 70%-ного (по объему) раствора серной кислоты, во второй сосуд той же вместимости налито 3 л раствора серной кислоты. Сколько литров раствора нужно перелить из второго сосуда в первый, чтобы в нем получился 7 %-ный раствор серной кислоты? Найдите все r, при которых задача имеет решение.

Решение:

Пусть из второго сосуда перелито в первый х литров раствора. Сразу отметим, что по условию

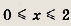
Для нахождения чистой кислоты в новом растворе получаем равенство

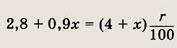
откуда

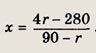
Теперь, учитывая, что х е [0; 2], заключаем, что х € [0 ;- 2], заключаем, что задача имеет решение лишь при

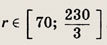
Задание 50.

Даны три сплава. Первый сплав содержит 70% олова и 30% свинца, второй — 80% олова и 20% цинка, третий — 50% олова, 10% свинца и 40% цинка. Из них получили сплав, содержащий 15% свинца. Какое наибольшее и какое наименьшее процентное содержание олова может быть в этом сплаве?

Ответ:

75% и 55%

Задание 51.

Имеются три сплава. Первый сплав содержит 30% никеля и 70% меди, второй — 10% меди и 90% марганца, третий — 15% никеля, 25% меди и 60% марганца. Из них необходимо приготовить новый сплав, содержащий 40% марганца. Какое наименьшее и какое наибольшее процентное содержание меди может быть в этом новом сплаве?

Решение:

Пусть взяты массы (в кг) первого, второго и третьего сплавов соответственно х, у и z. Новый сплав будет содержать (0,9y + 0,6z) марганца. По условию

0,9y + 0,6z = 0,4(x + у + z), т. е. 4x = 5у + 2z.

Найдем процентное содержание меди в новом сплаве. Имеем

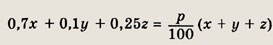
т. е.

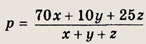
Подставляя в это соотношение

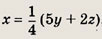
получаем

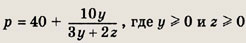
Таким образом, наименьшее значение р равно 40 и достигается при у = 0. Если у # 0, то, записав
р в виде

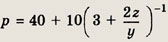
заключаем, что наибольшее значение р получается при z = 0 и оно равно

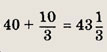
Ответ:

40% и 43 %

• Рассмотрим задачи на движение, работу, на части. Эти задачи решаются довольно однотипно, если подходящим образом выбрать искомые переменные величины. В задачах на движение в качестве этих переменных величин чаще всего выбирают пройденный путь и скорость, а в задачах на работу — объем всей работы и производительность каждого рабочего.

Задание 52.

На некотором участке средняя скорость поезда была ниже на 20%, чем предусмотрено расписанием. На сколько процентов увеличилось время прохождения этого участка пути?

Ответ:

25%

Задание 53.

Выйдя со станции с опозданием на 20 мин, поезд прошел перегон в 160 км со скоростью, превышающей скорость по расписанию на 16 км/ч, и пришел к концу перегона вовремя. Какова по расписанию скорость поезда на этом перегоне?

Ответ:

80 км/ч.

Задание 54.

Автомобиль проходит расстояние от пункта А до пункта В с постоянной скоростью. Если бы он увеличил скорость на 6 км/ч, то на прохождение пути затратил бы на 4 ч меньше. При езде со скоростью на 6 км/ч меньше начальной он потратил бы на б ч больше. Найдите расстояние между пунктами А и В.

Ответ:

720 км.

Задание 55.

Две автомашины, выехав одновременно из городов А и В навстречу друг другу, встретились через 6 ч. Первой машине, чтобы пройти 2/5 пути от А до В, требуется на 2 ч больше, чем второй для того, чтобы пройти 2/15 пути от В до А. За сколько часов проходит расстояние между городами А и В каждая машина?

Решение:

Пусть s — расстояние между городами А и В; х, у — скорости (км/ч) первого и второго автомобилей соответственно. Тогда по условию

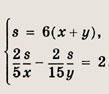
Эта система уравнений содержит три неизвестные величины. Но в задаче требуется найти только

t₁ = s/x и t₂ = s/y.

Запишем систему уравнений относительно неизвестных t₁ и t₂:

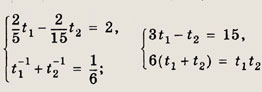
Подставляя t₂ = 3t₁ - 15 во второе уравнение, получим t₁ = 10 (второе решение t₁ = 3 не подходит, так как в этом случае t₂ = 3t₁ - 15 = -6 не имеет смысла), а тогда t₂ = 15.

Ответ:

за 10 и 15 ч.

Задание 56.

Пассажир, следующий из города А в город В, половину затраченного на весь путь времени ехал на автобусе, а половину времени на автомобиле. Если бы весь путь от А до В он проехал на автобусе, то это заняло бы у него в полтора раза больше времени. Во сколько раз автомобиль быстрее проезжает путь от А до В, чем автобус?

Ответ:

В 2 раза

Задание 57.

Два туриста вышли из А в В одновременно, причем первый турист каждый километр пути проходил на 5 мин быстрее второго. Первый, пройдя пятую часть пути, вернулся в A и, пробыв там 10 мин, снова пошел в Б. При этом оба туриста в В пришли одновременно. Каково расстояние от А до В, если второй турист прошел его за 2,5 ч?

Ответ:

10 км.

Задание 58.

Из А в В в разное время выехали по одному и тому же маршруту грузовик и автобус. Скорость автобуса на 12 км/ч больше скорости грузовика. Они прибыли в В одновременно. За 2,5 ч до их прибытия в В навстречу им из В выехал мотоцикл, который встретил грузовик на 10 мин раньше, чем автобус. Найдите скорость грузовика, если она вдвое меньше скорости мотоцикла.

Ответ:

36 км/ч.

Задание 59.

Из города А в город В с интервалом в 10 мин отправились три рейсовых автобуса. Первый автобус шел со скоростью на 5 км/ч меньше положенной, второй сохранял положенную скорость, а третий превышал ее на 6 км/ч. В результате все три автобуса пришли в Б одновременно. Определите расстояние между городами A и B.

Решение:

Пусть s — искомое расстояние от А до В, х (км/ч) — первоначально предполагаемая скорость рейсовых автобусов. Тогда по условию имеем систему .

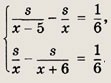
Вычитая из первого уравнения второе, получаем

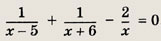
откуда х = 60. Теперь находим s = 110 км.

Ответ:

110 км.

Задание 60.

Из пункта А в пункт С, находящийся на расстоянии 80 км от А, выехал мотоциклист. Навстречу ему одновременно с ним из пункта Б, находящегося между А и С на расстоянии 5 км от С, выехал велосипедист, а из пункта С — автомобиль. Через какое время встретились мотоциклист и велосипедист, если известно, что это произошло через 20 мин после того, как автомобиль догнал велосипедиста, а мотоциклист до встречи с автомобилем провел в пути вдвое больше времени, чем велосипедист до того, как его догнал автомобиль?

Ответ:

Задание 61.

Расстояние между пристанями А и В по реке 50 км, а по шоссе 40 км. Пассажир опоздал к отплытию теплохода из А на 1,5 ч. Он в тот же момент сел в такси и прибыл в пункт Б одновременно с теплоходом. Выяснилось, что скорость такси была на 55 км/ч больше скорости теплохода. Какова скорость теплохода?

Ответ:

25 км/ч.

Задание 62.

Если пароход и катер плывут по течению, то расстояние от А до Б пароход покрывает в 1,5 раза быстрее, чем катер. При этом катер за каждый час отстает от парохода на 8 км. Если же они плывут против течения реки, то пароход проходит путь от Б до А в 2 раза быстрее катера. Найдите скорость парохода в стоячей воде.

Ответ:

20 км/ч.

Задание 63.

Из пункта А в пункт B против течения реки вышла моторная лодка. В пути мотор сломался, и пока его 20 мин чинили, лодку снесло вниз по течению реки. Определите, на сколько часов позже лодка прибыла в пункт B, если обычно путь из А в B лодка проходит в 1,5 раза быстрее, чем путь из B в А.

Решение:

Пусть s — расстояние между городами A и В, х — скорость моторной лодки в стоячей воде, у — скорость течения реки. Тогда

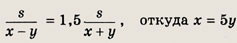
Время в пути, как следует из условия, равно

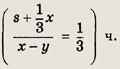
Искомая разность с учетом того, что х = 5у, составляет

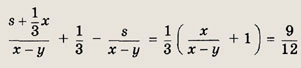
Ответ:

на 45 мин.

Задание 64.

Из пункта А в пункт Б в 12 ч вышел пешеход, одновременно навстречу ему из Б в А выехал велосипедист. По дороге велосипед сломался и простоял 15 мин. Двигаясь дальше, велосипедист встретился с пешеходом в 13 ч 30 мин. Если бы велосипедист не останавливался, то встреча произошла бы на 10 мин раньше. Считая скорости пешехода и велосипедиста постоянными, определите время прибытия пешехода в пункт В и велосипедиста в пункт А.

Ответ:

16 ч и 14 ч 15 мин.

Задание 65.

Из точек А и Б, расстояние между которыми равно 1 м, по прямой АВ начинают одновременно двигаться два тела. Первое тело начинает движение с постоянной скоростью из точки А по направлению к точке В, а второе — из точки В в том же направлении с начальной скоростью 16 м/с и с некоторым постоянным ускорением. Известно, что через 1 с после начала движения второе тело находилось от точки А на расстоянии не большем, чем 15 м, а еще через 1с — не меньшем, чем 25 м. Определите скорость первого тела, если через 3 е после начала движения расстояние между телами составляло 2 м.

Решение:

Рассмотрим числовую ось с началом в точке А и направлением от А к В; тогда получим A(0), В(1). Пусть v — скорость первого тела (v > 0), а — ускорение второго тела. Найдем координаты первого и второго тела в момент времени t:

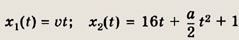
Из анализа условия задачи видно, что

Полагая t = 1 и t = 2, имеем

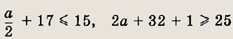
откуда а = -4. Расстояние между точками в момент времени t равно

s(t) = |x₁ (t) - x₂ (t)|

откуда при t = 3 согласно условию получим:

|3v - 49 + 2 • 9| = 2, |Зv - 21|= 2, т.е. Зv = 21 ± 2.

Ответ:

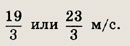
Задание 66.

За определенное время необходимо было изготовить 150 изделий. После изготовления 40 изделий стали изготавливать в день на 15 изделий больше и к сроку изготовили на 50% изделий больше, чем требовалось. Сколько изделий было изготовлено в первый день?

Ответ:

22

Задание 67.

Бригаде грузчиков поручили перевезти 120 контейнеров. После перевозки 36 контейнеров автомашину заменили более вместительной, грузоподъемность которой на 10 контейнеров больше. В результате общее число рейсов по сравнению с первоначально запланированным сократилось вдвое. Сколько контейнеров перевозила за один рейс первая машина?

Ответ: 4

4

Задание 68.

Первый рабочий может выполнить задание за 8 ч, а второй за 6 ч. Они работали вместе 2 ч, а заканчивал задание один второй рабочий. Сколько времени потребовалось для выполнения этого задания?

Ответ:

4,5ч.

Задание 69.

Двое рабочих, работая одновременно, выполнили задание за 5 дней. Если бы первый рабочий работал в 2 раза быстрее, а второй в 2 раза медленнее, то они выполнили бы задание за 4 дня. За сколько дней выполнил бы задание один первый рабочий?

Решение:

Пусть S — объем всего задания; х, у — производительность труда первого и второго рабочего соответственно (т. е. количество изделий, производимых рабочим за один день). Тогда по условию

а требуется найти величину

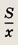
Решив эту систему, получаем 30х = 3S, откуда

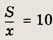
Ответ:

за 10 дней.

Задание 70.

Одна первая труба наполняет бассейн на 3 ч быстрее, чем одна вторая. Чтобы наполнить бассейн, открыли сразу обе трубы, но через 10 ч первую трубу закрыли и после этого одна вторая труба наполнила бассейн через 5 ч 45 мин. За какое время наполнится бассейн, если будет открыта одна первая труба?

Ответ:

24 ч.

Задание 71.

Бассейн наполняется водой из двух кранов. Сначала открыли первый кран на 1/3 часть того времени, за которое наполняет бассейн один второй кран. Затем был открыт один второй кран на 1/2 часть того времени, за которое наполняет бассейн первый кран. После этого оказалось, что уже заполнено 5/6 объема бассейна. За какое время наполняет бассейн каждый кран в отдельности, если открытые вместе они наполняют бассейн за 2,4 ч?

Решение:

Введем обозначения: S (м³) — объем бассейна; х, у (м³/ч) — производительность соответственно первого и второго кранов (т. е. количество воды в 1 м³, наливаемое краном в бассейн за 1 ч работы). Тогда по условию

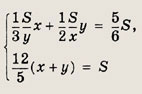
Удобно х из первого уравнения выразить через у:

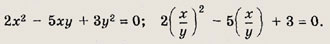
Отсюда либо х = у, либо х= 1,5у. Теперь находим: в первом случае

а во втором

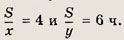
Оба варианта подходят.

Ответ:

за 4,8 ч каждый или за 4 и 6 ч.

 

Задание 72.

Два насоса различной мощности, работая вместе, наполняют бассейн за 4 ч. Для наполнения бассейна наполовину первому насосу требуется на 4 ч больше, чем второму насосу для наполнения 3/4 бассейна. За какое время может наполнить бассейн один второй насос?

Ответ:

5 ч 20 мин.

Задание 73.

Три тракторные бригады, работая вместе, вспахивают поле за 4 дня. Первая и вторая бригады вместе вспахали бы это поле за 6 дней, а вторая и третья — за 8 дней. Во сколько раз больше вспахивает за день вторая бригада, чем третья?

Ответ:

В 1,5 раза

Задание 74.

На предприятии работают три машинистки разной квалификации. Первая печатает в час на 2 страницы больше, чем вторая, а у третьей на печатание страницы уходит на 4 мин больше, чем у первой, и в 4/3 раза больше времени, чем у второй. Сколько страниц в час печатает первая машинистка?

Ответ:

10

Задание 75.

Каждому из трех экскаваторов для того чтобы вырыть котлован, требуется определенное время, причем третий экскаватор вырыл бы котлован на 1 ч 36 мин быстрее второго. Работая все вместе, они выполнят задание за 1 ч. Если первый экскаватор проработает 1 ч, а затем третий еще 1,6 ч, то они вместе также выроют весь котлован. За какое время может вырыть весь котлован каждый из экскаваторов, работая самостоятельно?

Решение:

Пусть S (м³) — объем котлована, х, у, z (м³/ч) — производительность каждого из экскаваторов. Из условия задачи вытекают следующие равенства:

откуда

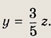
Подставляя

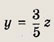
в первое равенство, находим

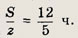
Тогда из первого уравнения получаем

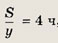
а из третьего

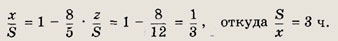
Ответ:

3 ч; 4 ч; 2,4 ч.

Задание 76.

Три цистерны одинакового объема начинают одновременно наполняться водой, причем в первую цистерну поступает 120 л воды в минуту, а во вторую — 40 л в минуту. Известно, что в начальный момент времени первая цистерна была пуста, а объем воды в третьей цистерне в 2 раза меньше, чем во второй, и что все три цистерны будут заполнены одновременно. Сколько литров воды поступает за одну минуту в третью цистерну?

Ответ:

80 лет

Задание 77.

Три бригады, работая вместе, могут выполнить некоторое задание за а дней. Если сначала в течение двух дней будет работать одна первая бригада, а затем в течение одного дня вторая и третья бригады, то выполненной окажется 1/3 часть этого задания. За какое время может выполнить все задание одна первая бригада?

Решение:

Пусть S —объем всего задания, х, у, z — производительность труда каждой бригады. Тогда

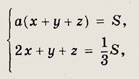
откуда получаем

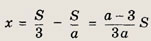
Так как

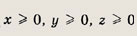
то из второго равенства следует, что

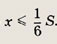
Отсюда

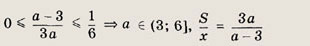
Ответ:

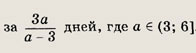
Задание 78.

Из пункта А в пункт В, расстояние между которыми равно 15 км, вышли одновременно два пешехода; в тот же момент из пункта В в пункт А выехал велосипедист. Проехав 1/k часть пути от В к А, велосипедист встретил первого пешехода, затем, проехав 2/3 всего пути, он встретил второго пешехода. На каком расстоянии s от них в момент встречи находился первый пешеход?

Ответ:

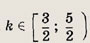
s = 10 , если

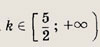
Задание 79.

Баржа отплыла от пристани вниз по течению реки; скорость течения равна и (км/ч). Когда баржа проплыла 3 км, от пристани вдогонку за ней отплыл катер, скорость которого в стоячей воде равна 9 км/ч. Катер догнал баржу и отбуксировал ее назад на пристань со скоростью 4 км/ч. Через какое время баржа была возвращена на пристань? При какой скорости и это время окажется наименьшим?

Решение:

Сначала найдем время, за которое катер догнал баржу. Получаем 3 + vt = (9 + u)t, т. е.

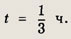
Таким образом, баржа шла по течению реки

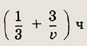
и прошла

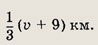
Обратный путь она проделала со скоростью 4 км/ч, затратив на него

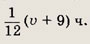
Значит, баржа была возвращена на пристань через

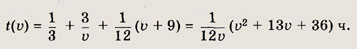
Найдем наименьшее значение t(v). Имеем

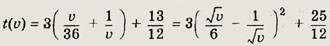
Следовательно, наименьшее значение t(v) достигается при

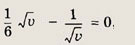
т. е. при v = 6.

Замечание:

Минимальное значение t(v) можно было найти, взяв производную этой функции. Задачи, решаемые с помощью применения производной, рассматриваются ниже.

Ответ:

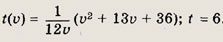
Задание 80.

Турист идет из пункта А, находящегося на шоссе, в пункт В, расположенный в 8 км от шоссе. Расстояние от А до В по прямой равно 17 км. В каком месте туристу следует свернуть с шоссе, чтобы в кратчайшее время прийти в пункт В, если скорость туриста по шоссе 5 км/ч, а по бездорожью 3 км/ч?

Ответ:

В 9 км от А

В задачах (81—84) по двум заданным комбинациям неизвестных требуется установить значение искомой третьей комбинации.

Задание 81.

Известно, что 10 кг картофеля, 15 кг свеклы, 10 кг моркови и 14 кг капусты стоят вместе 105,6 р., а 15 кг картофеля, 6 кг свеклы, 4 кг моркови и 21 кг капусты — 110 р. Какова общая стоимость 20 кг картофеля, 12 кг свеклы, 8 кг моркови и 28 кг капусты?

Решение:

Пусть х, у, z и t — цены в рублях за 1 кг картофеля, свеклы, моркови и капусты соответственно. Тогда по условию

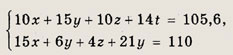
Требуется найти комбинацию

20х + 12у + 8z + 28t = N

Умножим первое уравнение системы на число

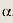
второе — на число ß и сложим. Получим следующее равенство:

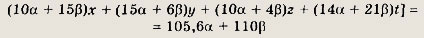
верное при любых

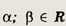
Подберем

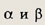
так, чтобы получилась искомая комбинация. Для этого должны выполняться равенства

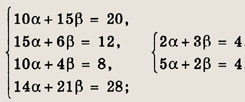
откуда

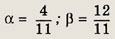
Итак, искомая цена составляет

Ответ:

158,4 р.

Задание 82.

Продаются пакеты акций акционерных обществ A, В, С и D. Пакет из 5 акций А, 1 акций В, 3 акций С и 4 акций D стоит 57 000 р., а пакет из 8 акций А, 2 акций B, 4 акций С и 3 акций D стоит 51 000 р. Сколько стоит пакет из 2 акций А, 12 акций Б, 2 акций С и 5 акций D?

Ответ:

63000 р.

Задание 83.

Гвоздь, три винта и два шурупа весят 24 г, а два гвоздя, пять винтов и четыре шурупа весят 44 г. Сколько граммов весят вместе гвоздь, четыре винта и два шурупа?

Ответ:

28 г.

Задание 84.

Имеются три типа станков разной производительности. При этом три станка первого типа, четыре второго и два третьего выполняют всю работу за 2 ч, два станка первого типа, пять второго и четыре третьего — за 3 ч. Объем работы увеличили в 3,5 раза и установили 21 станок первого типа, 42 второго и 24 третьего. За какое время будет выполнен этот объем работы?

Ответ:

За 1 ч.

 

В задачах 85—98 часть условий записывается в виде неравенств. Однако во всех этих задачах искомая величина является натуральным числом, что дает дополнительную информацию и позволяет однозначно установить ее значение.

Задание 85.

Бригады, состоящие из одинакового числа рабочих, получили на складе спецодежду. Каждый рабочий
получил по два комплекта спецодежды, а каждой бригаде выдали на 20 комплектов больше, чем было число бригад. Если бы бригад было на 4 больше, а каждой из бригад выдали бы по 12 комплектов, то спецодежды на складе не хватило бы. Сколько комплектов одежды было на складе?

Решение:

Пусть n — число бригад, m — число рабочих в каждой бригаде. Тогда условие задачи приводим к системе:

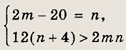
Для числа п получаем неравенство

n(n + 20) < 12(n + 4), т.е. n² + 8n - 48 < 0, откуда следует, что n € (-12; 4). Но величина n — натуральное число.

Следовательно, n = 1, n = 2 или n = 3. Учитывая, что

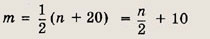
— также натуральное число (число рабочих в бригаде), получаем n = 2. Далее находим m = 11 и число комплектов спецодежды на складе: 2mn = 44.

Ответ:

44 комплекта

Задание 86.

Производительность первого автомобильного завода не превышает 950 машин в сутки. Производительность второго завода первоначально составляла 95% производительности первого завода. После ввода дополнительной линии второй завод увеличил производство машин в сутки на 23% от числа машин, производимых на первом заводе, и стал их выпускать более 1000 штук. Сколько автомобилей в сутки выпускал каждый завод до реконструкции второго завода?

Ответ:

900 и 855 машин

Задание 87.

Бригада маляров белила потолки в двух комнатах. Площадь потолка в первой комнате в 3 раза больше, чем во второй, и в первой комнате работало на 6 человек больше. Когда побелка потолка в первой комнате была закончена, во второй комнате еще работали. Какое наибольшее число маляров могло быть в бригаде, если все они начали работать одновременно и работали с одинаковой производительностью?

Ответ:

10 человек

Задание 88.

В двух бригадах более 27 человек рабочих. Число рабочих в первой бригаде более чем вдвое превышает число рабочих во второй бригаде, уменьшенное на 12. Число рабочих во второй бригаде более чем в 9 раз превышает число рабочих в первой бригаде, уменьшенное на 10. Сколько человек в каждой бригаде?

Ответ:

11 и 17 человек

Задание 89.

В двух ящиках находится более 29 одинаковых деталей. Число деталей в первом ящике, уменьшенное на 2, более чем в 3 раза превышает число деталей во втором ящике. Утроенное число деталей в первом ящике превышает удвоенное число деталей во втором ящике, но это превышение меньше 60. Сколько деталей в каждом ящике?

Решение:

Пусть m и n — число деталей в первом и во втором ящиках соответственно. Тогда из условия задачи вытекает следующая система неравенств:

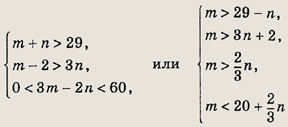
откуда

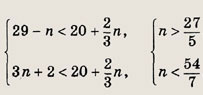
Учитывая, что n — натуральное число, получаем n = 6, n = 7. Проверяя каждое из этих значений, заключаем, что всем неравенствам системы удовлетворяют только числа n = 7 и m = 24.

Ответ:

24 детали в первом ящике и 7 деталей во втором

Задание 90.

При отделке квартир в новом доме используются три типа оконных рам, поставляемых в комплектах (в каждом комплекте некоторое количество рам одного типа). На стройку привезли по одному комплекту рам первого и второго типа и четыре комплекта третьего типа. Оказалось, что количество окон в доме на 2 больше, чем общее количество рам в этих комплектах. Если бы завезли четыре комплекта рам первого типа и один третьего, то 85 окон оказалось бы без рам. Если же поставить четыре комплекта второго типа и один третьего, то не хватило бы 53 рамы. Известно, что какое-то количество окон останется без рам, если поставить по три комплекта рам каждого типа. Сколько окон в доме?

Ответ:

124 окна

Задание 91.

В киоске продаются три вида наборов игрушек: деревянные, пластиковые и мягкие. Для детского сада купили по одному набору деревянных и пластиковых игрушек и четыре набора мягких. При этом каждый ребенок получил по одной игрушке. Если бы было куплено четыре набора деревянных игрушек и один набор мягких игрушек, то 57 детям игрушек не досталось бы, а если бы купили четыре набора пластиковых и один набор мягких игрушек, то 41 ребенок остался бы без игрушки. Сколько всего детей в детском саду, если, купив по три набора игрушек каждого вида, сад не обеспечил бы всех детей игрушками?

Решение:

Пусть m, n, k — числа деревянных, пластиковых и мягких игрушек в каждом из типов наборов, N — число детей в детском саду. Тогда условие задачи приводит к системе

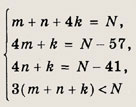
Выразим через N величины m, n и k из первых трех равенств. Вычитая из первого уравнения, умноженного на 4, сумму второго и третьего уравнений, получим

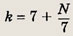
откуда, в частности, следует, что число N нацело делится на 7. Теперь выражаем m и n:

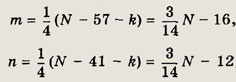
откуда, в частности, следует, что

нацело делится на 14. Подставив найденные для m, n и k выражения в последнее неравенство системы, получим:

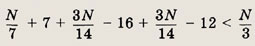
т. е.

Нужно найти целое число N, делящееся нацело на 14 и удовлетворяющее неравенствам

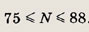
Такое число только одно: N = 84.

Ответ:

84 ребенка

Задание 92.

Между городами А и В летают самолеты трех типов. Каждый самолет первого, второго и третьего типа может принять на борт соответственно 230, 110 и 40 пассажиров, а также 27, 12 и 5 контейнеров. Все самолеты этой линии могут принять на борт 760 пассажиров и 88 контейнеров. Найдите число самолетов каждого типа, если их общее число на этой линии не более восьми.

Ответ:

2; 2; 2

Задание 93.

Завод имеет сборочные линии трех типов. На каждой линии первого, второго и третьего типа ежедневно собираются 100, 400 и 30 приемников первого класса и 19, 69 и 5 приемников высшего класса соответственно. В сумме на всех линиях ежедневно собирается 1030 приемников первого класса и 181 приемник высшего класса. Сколько линий каждого типа на заводе, если их общее число не превосходит 10?

Решение:

Пусть m, n и k — число линий первого, второго и третьего типа. Тогда

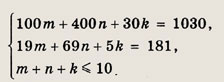
где m, n и k — натуральные числа. Легко видеть, что n = 1 или n = 2. Получаем системы

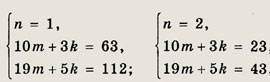
откуда следует, что m = 3, n = 1, k =11 (из первой системы) и m = 2, n = 2, k = 1 (из второй). Первая тройка чисел не подходит в силу записанного неравенства.

Ответ:

2; 2; 1

Задание 94.

В каждом классе средней школы одинаковое число парт. Во время ремонта парты со второго этажа увозили на грузовике по 5 штук, а в последний рейс осталось 2 парты. С третьего этажа парты увозили на другом грузовике по 7 штук, а в последний рейс осталось 4 парты. Второй грузовик сделал на один рейс больше, чем первый. Сколько парт было в каждом классе?

Ответ:

41

Задание 95.

На станцию привезли несколько одинаковых контейнеров, заполненных телевизорами. Телевизоры перегрузили в вагоны одинаковой вместимости. Получилось 7 полных вагонов и еще осталось 5 телевизоров. Через неделю привезли другое количество таких же контейнеров. При перегрузке получилось 11 полных вагонов, а в 12-м не хватало одного телевизора для полной загрузки. Сколько телевизоров вмещает контейнер, если это число больше единицы?

Решение:

Пусть m — число телевизоров, которое вмещает каждый вагон, а n — число телевизоров в каждом контейнере. Тогда по условию задачи

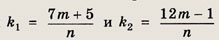
— это целые числа, равные числу контейнеров, пришедших на станцию в первый и во второй раз. Исключим из этих соотношений переменную т, умножая первое равенство на 12, второе на 7 и вычитая результаты друг из друга.

Получим

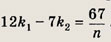
— также целое число. Значит, n должно быть натуральным делителем числа 67. Отсюда либо n = 67, либо n = 1 (что не подходит по условию).

Ответ:

67 телевизоров

Задание 96.

В упаковочном цехе конфеты из одинаковых контейнеров перекладывают в коробки одинаковой вместимости. Первый упаковщик разложил все конфеты из трех контейнеров, причем для заполнения последней коробки ему еще не хватило 5 конфет. Второй упаковщик перекладывал конфеты из шести контейнеров, 7 конфет отложил, а остальными без остатка заполнил некоторое количество коробок. Сколько конфет в каждой коробке, если это число больше 1?

Ответ:

17 конфет

Задание 97.

Рота солдат прибыла на парад в полном составе прямоугольным строем по 24 человека в ряд. По прибытии оказалось, что не все солдаты могут участвовать в параде. Оставшийся для парада состав роты перестроили так, что число рядов стало на 2 меньше, а число солдат в каждом ряду стало на 26 больше числа новых рядов. Известно, что если бы все солдаты участвовали в параде, то роту можно было бы выстроить так, что число солдат в каждом ряду совпало бы с числом рядов. Сколько солдат было в роте?

Ответ:

144 солдата

Задание 98.

Число деталей, изготовленных за смену первой бригадой, равно 115% от числа деталей, изготовленных за смену второй бригадой. Продукцию двух бригад упаковали в два ящика. В первом ящике оказалось 2/3 числа деталей, изготовленных первой бригадой, и 1/7 часть деталей, изготовленных второй бригадой. Сколько деталей в первом ящике изготовлено первой бригадой и сколько второй, если в первом ящике оказалось менее 1000 деталей, а во втором — более 1000 деталей?

Ответ:

644 и 120 деталей

 

При решении задач на движение часто возникают системы, содержащие уравнения и неравенства (99—102).

Задание 99.

Пункты А и В расположены на реке так, что плот, плывущий из А в В со скоростью течения реки, проходит путь от А до В за 24 ч. Весь путь от А до В и обратно моторная лодка проходит не менее чем за 10 ч. Если бы собственная скорость моторной лодки увеличилась на 40%, то тот же путь (от А до В и обратно) занял бы у лодки не более 7 ч. Найдите время, за которое моторная лодка проходит путь от А до В.

Решение:

Пусть s (км) — расстояние между пунктами A и В, х (км/ч) — скорость течения реки, у (км/ч) — собственная скорость моторной лодки. Тогда согласно условию получаем систему

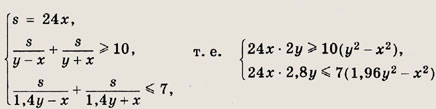
Преобразуя неравенства, имеем

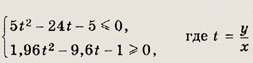
Единственным числом, удовлетворяющим обоим неравенствам, является t = 5, т. е. у = 5х. Теперь находим требуемое время

Ответ:

4 ч.

Задание 100.

Утром из пункта А в пункт В отправляется по течению реки моторная лодка. Одновременно из В в А выходит катер, собственная скорость которого в 1,4 раза больше собственной скорости моторной лодки. Известно, что лодка и катер встречаются в 12 ч дня, затем лодка прибывает в пункт В не позже 15 ч дня, а катер прибывает в А не раньше 15 ч дня. Найдите время отправления лодки из пункта А в пункт В, если известно, что на путь из В в А лодка затрачивает не более 9 ч, а катер на путь из А в В затрачивает не менее 4,5 ч.

Ответ:

9 ч утра.

Задание 101.

В 9 ч утра из пункта А выезжает велосипедист, который едет до пункта В. Через 2 ч после отправления велосипедиста из А в В выезжает автомобилист, который догоняет велосипедиста не позже 12 ч дня. Продолжая движение, автомобилист прибывает в пункт В, в тот же момент поворачивает и едет из Б в А. На этом пути автомобилист снова встречает велосипедиста и потом прибывает в пункт А в 17 ч того же дня. Найдите время прибытия велосипедиста в пункт В, если известно, что между двумя встречами велосипедиста и автомобилиста прошло не более 3 ч.

Ответ:

18 ч.

Задание 102.

Деревня расположена на берегу реки, а школа — на шоссе, пересекающем реку под прямым углом. Зимой школьник ходит из деревни в школу напрямик на лыжах и тратит на дорогу 40 мин. Весной, в распутицу, он идет берегом реки до шоссе, а дальше — по шоссе до школы, и тратит на дорогу 1 ч 10 мин. Наконец, осенью он проходит вдоль реки половину расстояния, отделяющего деревню от шоссе, а дальше идет напрямик. При этом он доходит до школы быстрее, чем за 57 мин. Установите, что дальше: деревня от шоссе или школа от реки, если известно, что пешком школьник ходит всегда с одной и той же скоростью, а на лыжах — со скоростью на 25% большей (реку и шоссе можно считать прямолинейными траекториями).

Ответ:

В задачах 103—109 для нахождения оптимального варианта снова нужно использовать тот факт, что искомые переменные величины — целые числа.

Задание103.

Завод должен прислать заказчику 1100 деталей. Детали для пересылки упаковываются в ящики. Имеются ящики трех типов. Один ящик первого типа вмещает 70 деталей, один ящик второго типа — 40 деталей, а один ящик третьего типа — 25 деталей. Стоимость пересылки одного ящика первого типа равна 200 р., стоимость пересылки одного ящика второго типа — 100 р., а третьего — 70 р. Сколько ящиков каждого типа должен использовать завод, чтобы стоимость пересылки была наименьшей (недогрузка ящиков не допускается)?

Решение:

Пусть m, n и k — требуемое число ящиков каждого типа. Тогда должно выполняться равенство

70m + 40n + 25k = 1100, а величина N = 200m + 100n + 70k должна быть минимально возможной. Найдем себестоимость пересылки одной детали в каждом из ящиков. Получаем

Поэтому мы должны взять максимально возможное число ящиков второго типа и минимальное число ящиков первого типа. Итак, m = 0, n = 25, k = 4.

Ответ:

0, 25 и 4

Задание 104.

Ученики второго, третьего и четвертого классов собирали макулатуру. Каждый второклассник работал по 3 дня, третьеклассник по 12 дней, четвероклассник — по 16 дней. При этом каждый второклассник собрал 30 кг макулатуры, каждый третьеклассник — 130 кг, а каждый четвероклассник — 170 кг. Все дети вместе отработали 95 дней. Сколько учеников каждого класса участвовало в работе, если общее количество собранной макулатуры оказалось максимальным?

Ответ:

1; 5; 2

Задание 105.

Для детского сада приобретают на сумму 1320 р. наборы конфет трех типов. Наборы из 50 конфет стоят 30 р., наборы из 190 конфет — 104 р., а наборы из 160 конфет — 90 р. Сколько наборов каждого типа можно купить для детского сада, чтобы общее количество купленных конфет было максимальным?

Ответ:

2; 0; 14

Задание 106.

Из лесного хозяйства в город нужно вывезти 1590 деревьев. Для перевозки деревьев имеются полуторатонные, трехтонные и пятитонные машины. На полуторатонке за один рейс можно вывезти 26 деревьев, на трехтонке — 45 деревьев, а на пятитонке — 75 деревьев. Стоимость одного рейса для полуторатонной машины равна 90 р., для трехтонной — 150 р., а для пятитонной — 240 р. Как лесное хозяйство должно распределить перевозки, чтобы их стоимость была наименьшей (недогрузка машин не допускается)?

Ответ:

0; 2; 20

Задание 107.

В контейнер упакованы изделия двух типов. Стоимость и масса одного изделия составляют 400 р. и 12 кг для первого типа и 600 р. и 15 кг для второго типа. Общая масса изделий равна 321 кг. Определите минимальную и максимальную возможные стоимости находящихся в контейнере изделий.

Решение:

Пусть m и n — число изделий первого и второго типа. По условию,

12m + 15n = 321, т. е. 4m + 5n = 107.

Найдем стоимость такого контейнера:

р = 400m + 600n = 100(4m + 6n) = 100(107 + n)

Таким образом, величина р будет максимальной при максимально возможном n и минимальной при минимальном n. При этом число

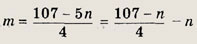
должно быть натуральным. Отсюда следует, что n = 3 — минимальное, а n = 19 — максимально возможное число контейнеров. Итак,

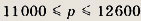
Ответ:

11000 р. и 12600р.

Задание 108.

Имеются три пакета акций. Общее суммарное количество акций первых двух пакетов совпадает с количеством акций в третьем пакете. Первый пакет в 4 раза дешевле второго, а суммарная стоимость первого и второго пакетов совпадает со стоимостью третьего пакета. Одна акция из второго пакета дороже одной акции из первого пакета на величину, заключенную в пределах от 16 до 20 долларов, а цена одной акции из третьего пакета не меньше 42 и не больше 60 долларов. Какой наименьший процент от общего количества акций может содержаться в первом пакете? какой наибольший?

Ответ:

12,5% и 15%

Задание 109.

Имеются три партии товара. Общее количество единиц товара, в первых двух партиях совпадает с общим количеством единиц товара в третьей партии. Вторая партия в 9 раз дороже первой, а суммарная стоимость первой и второй партии совпадает со стоимостью третьей партии. Единица товара из первой партии дешевле единицы товара из второй партии на величину, заключенную в пределах от 35 до 40 р., а цена единицы товара из третьей партии не меньше 42 и не больше 56 р. Какой наименьший процент от общего количества единиц товара может содержаться в первой партии? какой наибольший?

Ответ:

10% и 15%

Задание 110.

На биржу выставлены пакеты акций трех инвестиционных проектов. Один пакет акций первого проекта стоит 200 тыс. р. и предусматривает создание 30 новых рабочих мест. Один пакет акций второго проекта стоит 180 тыс. р. и предусматривает создание 24 новых рабочих мест. Аналогичные показатели третьего проекта — 300 тыс. р. и 28 рабочих мест. Определите максимальное и минимальное значения суммарной стоимости проданных пакетов акций, если известно, что вырученные от продажи деньги позволяют создать 1184 новых рабочих места.

Ответ:

12300 тыс. р. и 8160 тыс. р.

Задание 111.

На биржу выставлены пакеты акций трех инвестиционных проектов. Один пакет акций первого проекта стоит 150 тыс. р. и предусматривает создание 14 новых рабочих мест. Один пакет акций второго проекта стоит 90 тыс. р. и предусматривает создание 12 новых рабочих мест. Аналогичные показатели третьего поректа — 100 тыс. р. и 15 рабочих мест. Определите максимальное и минимальное значения суммарной стоимости проданных пакетов акций, если известно, что вырученные от продажи деньги позволяют создать 599 новых рабочих мест.

Ответ:

111. 6800 тыс. р. и 4050 тыс. р.

Задание 112.

На продажу выставлены земельные участки под кооперативные дома, коттеджи и садовые домики. Под один кооперативный дом на 60 семей выделяется участок стоимостью 100 тыс. р.; под один коттеджный кооператив на 48 семей — участок за 90 тыс. р.; под один садовый кооператив на 56 семей — участок за 150 тыс. р. Определите максимальное и минимальное значения суммарной стоимости проданных участков, если известно, что покупатели земли предполагают построить жилье для 2368 семей.

Ответ:

6150 тыс. р. и 4080 тыс. р.

Задание 113.

На продажу выставлены земельные участки под кооперативные дома, коттеджи и садовые домики. Под один кооперативный дом на 70 семей выделяется участок площадью 520 соток; под один коттеджный кооператив на 40 семей — 320 соток; под один садовый кооператив на 52 семьи — 480 соток. Определите максимальное и минимальное значения суммарной площади проданных участков, если известно, что покупатели земли предполагают построить жилье для 1502 семей.

Ответ:

13640 и 11320 соток

Задание 114.

Правительство решило закрыть нерентабельные шахты и построить новые фабрики и заводы. В результате закрытия одной шахты увольняется 180 человек, при этом на консервацию шахты и выплату пособий увольняемым выплачивается 52 млн р. Строительство одного нового завода с персоналом 170 человек стоит 43 млн р., а одной фабрики с персоналом 110 человек — 20 млн р. Чему равно максимально возможное увеличение суммарного числа новых рабочих мест, если известно, что сумма всех затрат правительства составила 714 млн р.?

Ответ:

2530 чел.

Задание 115.

Правительство решило закрыть нерентабельные шахты и построить новые фабрики и заводы. В результате закрытия одной шахты увольняется 180 человек, при этом на консервацию шахты и выплату пособий увольняемым выплачивается 52 млн р. Строительство одного нового завода с персоналом 170 человек стоит 43 млн р., а одной фабрики с персоналом 110 человек — 20 млн р. Чему равно максимально возможное сокращение суммарного числа рабочих мест, если известно, что сумма всех затрат правительства составила 714 млн р.?

Ответ:

400 чел.

Задание 116.

На двух шахтах добывается руда: на первой — 140 т в день, на второй — 160 т в день. Эта руда ежедневно перерабатывается на двух заводах, причем первый завод может перерабатывать в день не более 220 т руды, а второй — не более 180 т. Стоимость перевозок одной тонны руды от шахты до завода (в условных единицах) определяется из таблицы:

	Первый завод	Второй завод
Первая шахта	45	48
Вторая шахта	39	44

Сколько тонн руды нужно возить с каждой шахты на каждый завод, чтобы общая стоимость перевозок была наименьшей?

Ответ:

С первой шахты 60 т на первый завод и 80 т на второй завод, со второй — все 160 т на первый завод.

 

• Задачи на прогрессии достаточно популярны на вступительных экзаменах. Напомним относящиеся к этой теме основные понятия.

Если имеется правило, по которому каждому натуральному числу n ставится в соответствие некоторое действительное число а_n, то говорят, что задана числовая последовательность а₁, а₂,..., а_n,... В частности, если для любого n& N выполняется равенство а_{n + 1}= а_n + d, где d — фиксированное число, то такая последовательность называется арифметической прогрессией с первым членом а₁ и разностью d.

Для арифметической прогрессии справедливы формулы:

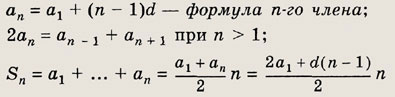
Если же последовательность b₁ ..., b_n, ... такова, что для любого n € N выполняется равенство

b_{n + 1} = b_n q, где q — фиксированное число, то такая последовательность называется геометрической прогрессией с первым членом b± и знаменателем q. Для геометрической прогрессии справедливы формулы:

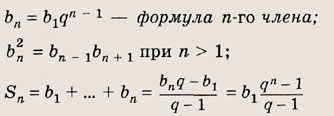
Наконец, отметим, что при |q| < 1 геометрическая прогрессия называется бесконечно убывающей. Для бесконечно убывающей геометрической прогрессии можно найти сумму всех ее членов:

При решении задач на прогрессии часто в качестве неизвестных выбираются первый член и разность (или знаменатель) этой прогрессии.

Задание 117.

Сумма второго и шестого членов арифметической прогрессии равна 7,2, а сумма третьего и восьмого членов этой прогрессии равна 8,4. Найдите разность прогрессии.

Ответ:

0,4

Задание 118.

Сумма первого и пятого членов арифметической прогрессии равна 5/3, а произведение третьего и четвертого ее членов равно 65/72. Найдите сумму семнадцати первых членов прогрессии.

Решение:

Пусть а₁ и d — первый член и разность прогрессии. Тогда по условию

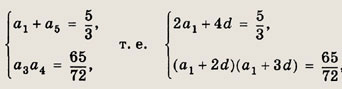
откуда

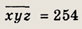
Поэтому второе уравнение системы преобразуется к виду

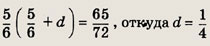
Следовательно,

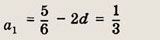
Теперь найдем требуемую сумму

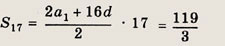
Ответ:

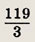
Задание 119.

Первый и четвертый члены геометрической прогрессии равны соответственно 64 и 8. Найдите сумму первых пяти ее членов.

Ответ:

124

Задание 120.

Сумма второго и пятого членов геометрической прогрессии равна 84, а сумма первого и третьего членов этой же прогрессии больше второго его члена на 7. Найдите четвертый член прогрессии

Решение:

Пусть b₁ и q — первый член и знаменатель прогрессии. Тогда по условию

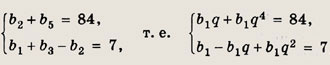
откуда, разделив первое уравнение на второе, имеем q(q + 1) = 12. Следовательно, q = -4 или q = 3. Из первого уравнения получаем

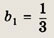
(при q = -4) или b₁ = 1 (при q = 3). Теперь находим b₄ = 27 или

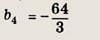
Ответ:

Задание 121.

Сумма первых трех членов геометрической прогрессии равна 26, а их произведение равно 216. Найдите первый член и знаменатель прогрессии.

Ответ:

2 и 3

Задание 122.

Три целых числа образуют геометрическую прогрессию. Найдите третий член этой прогрессии, если ее второй член на 1 больше первого и положителен.

Ответ:

4

Задание 123.

Найдите сумму первых 20 членов арифметической прогрессии, если известно, что сумма 3-го, 7-го, 14-го и 18-го членов этой прогрессии равна 10.

Ответ:

50

Задание 124.

Все члены арифметической прогрессии — натуральные числа. Сумма первых девяти ее членов больше 200, но меньше 220. Найдите первый член и разность прогрессии, если второй член равен 12.

Ответ:

8 и 4

Задание 125.

Турист, поднимаясь в гору, в первый час достиг высоты 800 м, а каждый следующий час поднимался на высоту, на 25 м меньшую, чем в предыдущий час. За сколько часов он достигнет высоты 5700 м?

Ответ:

За 8 ч.

Задание 126.

Периметр некоторого многоугольника равен 158 см, причем длины его сторон составляют арифметическую прогрессию, разность которой равна 3 см. Наибольшая сторона многоугольника равна 44 см. Сколько сторон имеет этот многоугольник?

Решение:

Стороны многоугольника образуют арифметическую прогрессию с первым членом a₁ = 44 и разностью d = -3. Если такой многоугольник имеет п сторон, то его периметр равен

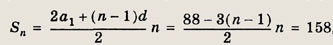
откуда для n получаем уравнение Зn² - 91n + 316 = 0. Решаем его и находим n = 4.

Ответ:

4

Задание 127.

Найдите число членов арифметической прогрессии, у которой сумма всех ее членов равна 112, произведение второго члена на разность прогрессии равна 30, а сумма третьего и пятого членов равна 32.

Ответ:

7

Задание 128.

На собрании акционеров было решено увеличить прибыль предприятия за счет расширения ассортимента продукции. Экономический анализ показал, что:

1) дополнительные доходы, приходящиеся на каждый новый вид продукции, окажутся равными 64 тыс. р. в год;

2) дополнительные расходы при освоении одного нового вида составляют 7 тыс. р. в год, а освоение каждого последующего вида потребует на 8 тыс. р. в год больше расходов, чем освоение предыдущего.
Найдите значение максимально возможного прироста прибыли.

Решение:

Дополнительные расходы на освоение одного нового вида продукции образуют арифметическую прогрессию с первым членом а₁ = 7 тыс. р. и разностью d = 8 тыс. р. Таким образом, расходы на освоение n-го вида составят

7 + (n - 1)8 = 8n - 1 (тыс. р.).

Освоение будет приносить доход до тех пор, пока 8n - 1 < 64, т. е.

Значит, получается максимально возможный прирост прибыли при освоении восьми новых видов продукции. Этот прирост равен

Ответ:

652 тыс. р.

Задание 129.

Сумма трех чисел, образующих арифметическую прогрессию, равна 30. Если вычесть из первого числа 5, из второго 4, а третье не менять, то полученные числа составят геометрическую прогрессию. Найдите эти числа.

Ответ:

17, 10 и 3 или 8, 10 и 12.

Задание 130.

Сумма первых 13 членов арифметической прогрессии равна 130. Известно, что 4-й, 10-й и 7-й члены этой прогрессии, взятые в указанном порядке, представляют собой три последовательных члена геометрической прогрессии. Найдите первый член арифметической прогрессии.

Ответ:

70 или 10

Задание 131.

Три числа составляют геометрическую прогрессию. Если из третьего числа вычесть 4, то числа составят арифметическую прогрессию. Если же из второго и третьего членов полученной арифметической прогрессии вычесть по 1, то снова получится геометрическая прогрессия. Найдите эти числа.

Ответ:

1, 3, 9 или

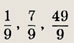
Задание 132.

Сумма членов бесконечно убывающей геометрической прогрессии равна 3/2, а сумма квадратов ее членов равна 1/8. Найдите знаменатель прогрессии.

Решение:

Пусть b₁ и q — первый член и знаменатель прогрессии. Тогда последовательность, состоящая из квадратов членов данной геометрической прогрессии, также является геометрической
прогрессией с первым членом b₁ и знаменателем q₂ . Используя формулу суммы всех членов бесконечно убывающей прогрессии, получаем

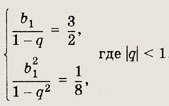
Подставляя во второе уравнение

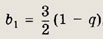
находим

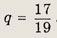
Ответ:

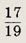
Задание 133.

Сумма кубов всех членов бесконечно убывающей геометрической прогрессии относится к сумме квадратов всех ее членов как 12:13. Сумма первых двух членов прогрессии равна 4/3. Найдите первый член и знаменатель прогрессии.

Ответ:

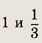
Задание 134.

Найдите сумму бесконечно убывающей геометрической прогрессии, второй член которой, удвоенное произведение первого члена на четвертый и третий член, взятые в указанном порядке, образуют арифметическую прогрессию с разностью 1/3.

Ответ:

Задание 135.

Представьте десятичную периодическую дробь 7,2(3) в виде обыкновенной дроби.

Ответ:

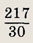
Задание 136.

Решите уравнение х³ + Зх² - 6х + а = 0, зная, что оно имеет три различных действительных корня, образующих геометрическую прогрессию.

Решение:

Если

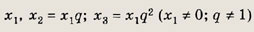
— три различных решения уравнения, то

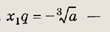
решение этого уравнения. Подставляя вместо х значение

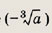
в уравнение, находим: a₁ = -8; а₂ = 0. Проверкой убеждаемся, что а = 0 не подходит. Решая уравнение при а = -8, т. е.

х⁶ + Зх² - 6x - 8 = 0,

получаем корни х₁ = -4, х₂ = 2, х₃ = -1, образующие геометрическую прогрессию.

Ответ:

-4; 2; -1

Задание 137.

При каких значениях параметра а четыре корня уравнения

х⁴ + (а - 3)х² + (а + 10)² = 0

являются последовательными членами арифметической прогрессии?

Ответ:

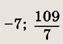
Задание 138.

Четырехзначное натуральное число А оканчивается цифрой 1. Двузначное число, образованное цифрами в разряде тысяч и сотен, цифра десятков и цифра единиц числа А в указанном порядке представляют собой три последовательных члена арифметической прогрессии. Из всех чисел А, удовлетворяющих указанным условиям, найдите то, у которого разность между цифрой десятков и цифрой сотен имеет наименьшее возможное значение.

Ответ:

1791

Задание 139.

Натуральные числа а, b и с, взятые в указанном порядке, образуют возрастающую геометрическую прогрессию, знаменатель которой является целым числом. Числа 2240 и 4312 делятся без остатка на b и с соответственно. Найдите числа а, b и с, если известно, что при указанных условиях сумма а + b + с максимально возможная.

Ответ:

2; 56; 392

 

При решении задач 140—147 воспользуйтесь тем, что если а₀ — цифра в разряде единиц, аr — цифра в разряде десятков и т. д. в записи (n + 1)-значного натурального числа А, то это число записывается в виде

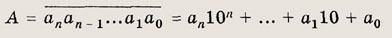
Задание 140.

Двузначное натуральное число С в 3 раза меньше квадрата суммы своих цифр. Найдите число С.

Решение:

1) Пусть х, у — цифры искомого числа С. Тогда С = 10х + у. По условию (х + у)² = 3(10х + у), где

х # 0, х, у -— целые числа от 0 до 9. Запишем полученное уравнение в виде

(х + у)² - 3(х + у) - 27х = 0

решим его относительно (х + у). Находим

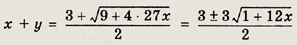
Сумма х + у > 0, поэтому

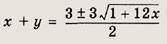
— натуральное число.

Подставляя х = 1, 2, ..., 9, заключаем, что это возможно лишь при х = 2 (тогда у = 7) и при х = 4 (тогда у = 8). Итак, условиям задачи удовлетворяют числа 27 и 48.

2) Приведем еще другой способ решения задачи, основанный на делимости целых чисел нацело. Вместо решения уравнения относительно (х + у) перепишем его в виде

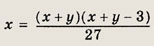
Так как х — натуральное число, то хотя бы один из сомножителей должен нацело делиться на 9

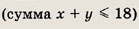
Отсюда либо х + у = = 18, либо х + у = 9, либо х + у - 3 = 9.

Если х + у = 18, то

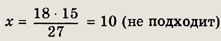
если

если

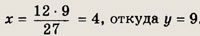
Получаем те же два числа: 27 и 48.

Ответ :

27 и 48

Задание 141.

Квадрат суммы цифр двузначного числа В относится к числу (B + 2) как 10 : 3. Найдите число В.

Ответ:

28

Задание 142.

Сумма трехзначного натурального числа А и числа, записанного теми же цифрами, но в обратном порядке, равна 1271. Из всех чисел А, удовлетворяющих указанным условиям, найдите наибольшее.

Решение:

Пусть искомое число А = 100х + 10у + z, где х # 0, у, z — цифры этого числа. Тогда число, записанное теми же цифрами, но в обратном порядке, имеет вид В = 100z +10y +х. По условию

101х + 20у+ 101z = 1271

Так как 1271 = 101 • 12 + 59, то это равенство можно переписать в виде

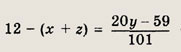
— целое число.

Отсюда следует, что у - 8, а тогда х + z = 11. Наибольшее число

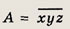
получается при х = 9, у = 8, z = 2.

Ответ:

982

Задание 143.

Натуральное трехзначное число В сложили с трехзначным натуральным числом, у которого цифры единиц и сотен равны цифрам сотен и единиц числа В соответственно, а цифра десятков совпадает с цифрой десятков числа Б. В сумме получили 1049.

Из всех чисел Б, удовлетворяющих указанным условиям, найдите наименьшее.

Ответ:

871

Задание 144.

Число C записывается теми же цифрами, что и четырехзначное натуральное число С, но взятыми в обратном порядке. Разность между С и С₁равна 270. Из всех таких чисел С найдите наименьшее, если известно, что произведение его цифр сотен и десятков принимает наибольшее возможное значение.

Решение:

Пусть С = 1000х + 100у +10z + t, где х # О, у, z и t — цифры этого числа.

Тогда C₁ = 1000t + 100z + 10y + z.

По условию

С - С₁ = 999(х - t) + 90(y - z) = 270

Сокращая это равенство на 9, получаем уравнение

111(х- t = 30- 10(y - z),

откуда следует, что число 111(х - t) должно нацело делиться на 10. Так как х и t — цифры, то это возможно лишь при х - t = 0. Значит, х = t, а поскольку мы ищем наименьшее возможное число, должно быть х = t = 1. Далее получаем у - z = 3. Учитывая, что произведение уz принимает наибольшее возможное значение, находим у = 9, z = 6. Итак, искомое число С = 1961.

Ответ:

1961

Задание 145.

Натуральное трехзначное число B, уменьшенное на 18, делится без остатка на 6, причем частное от такого деления равно произведению цифр десятков и единиц числа B. Найдите число B, если известно, что при делении этого числа на произведение цифр десятков и сотен в частном получается 25 и в остатке 8, а при делении на произведение цифр сотен и единиц в частном получается 16 и в остатке 1.

Ответ:

258

Задание 146.

При делении натурального трехзначного числа А на произведение цифр сотен и десятков получили в частном 25 и в остатке 4, а при делении на произведение цифр десятков и единиц — в частном 12 и в остатке 14. Кроме того, известно, что число (А - 6) делится на 31 без остатка, причем частное от такого деления равно произведению цифр сотен и единиц числа А. Найдите число А.

Решение:

Пусть

Тогда согласно условию

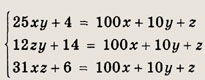
Из первого уравнения заключаем, что число (z - 4) делится без остатка на 5, а из второго — что число z является четным. Так как z — цифра, то z = 4. Теперь система преобразуется к виду (берем два последних уравнения)

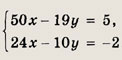
Решаем эту систему и находим х = 2; у = 5. Проверяем, что полученное число

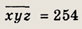
удовлетворяет также первому уравнению исходной системы.

Ответ:

254

Задание 147.

Из трех различных отличных от нуля цифр а, b и с составляют всевозможные различные трехзначные числа, причем каждая из указанных цифр встречается в записи числа один раз. Оказалось, что сумма всех этих чисел больше 2300, но не превосходит 2443. Найдите число

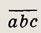
если известно, что оно четное и наибольшее из всех трехзначных чисел, удовлетворяющих условию задачи.


Решение:

Всего таких чисел шесть, причем в разряде сотен, десятков и единиц каждая цифра встречается по два раза. Следовательно, сумма всех таких чисел равна

2(а + b + с)100 + 2(а + b + с)10 + 2(а + b + с) = 222(а + b + с).

По условию,

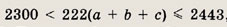
откуда целое число а + b + с равно 11. Теперь выбираем а, Ь, с так, чтобы они были различными, отличными от нуля, а число abc было четным и наибольшим из возможных. Получаем с = 2; b = 1; а = 8.

Ответ:

812