Варианты проверочных работ
Вариант 1
Постройте графики следующих функций и уравнений (1-5):
Задание 1.
Зх - 2у = 6
Задание 2.
у = -(х2 + 4х + 3)
Задание 3.
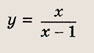
Задание 4.
х2 + х + у2 - 2у = 0
Задание 5.
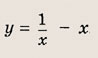
Задание 6.
Запишите уравнение прямой, проходящей через точку А(2; -1) перпендикулярно прямой 2х - у + 3 = 0.
Задание 7.
Запишите уравнение образа параболы у = х2 + 6х + + 3 при параллельном переносе, если ее вершина смещается в точку пересечения прямых х + 2у-3 = 0 и 2х + 3у - 7 = 0.
Задание 8.
Найдите число решений уравнения

в зависимости от а.
Вариант 2
Постройте графики следующих функций и уравнений (1-5).
Задание 1.
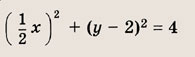
Задание 2.
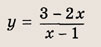
Задание 3.
у2 - 5ху + 6х2 + Зх - у = 0
Задание 4.
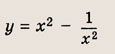
Задание 5.
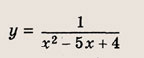
Задание 6.
Окружность, центром которой является точка пересечения прямых 2х - у - 3 = 0 и х + 3у + 2 = 0, касается прямой х + у = 2. Запишите уравнение этой окружности.
Задание 7.
Решите систему неравенств
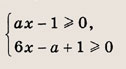
Задание 8.
Найдите все значения параметра а, при которых система уравнений
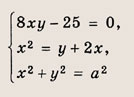
имеет решения.
Вариант 3
Постройте графики следующих функций и уравнений (1-4):
Задание 1.
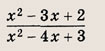
Задание 2.
4х2 + у2 - 24х - 4у + 36 = 0
Задание З.

Задание 4.
у(х2 - 1) = 2х
Задание 5.
При каких а расстояние между прямыми 2х + у = 2 и 2х + у - а равно

Задание 6.
При каком значении параметра а система неравенств
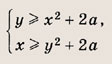
имеет единственное решение?
Задание 7.
Найдите минимальное значение величины ху + 5х - 2у, если х2 + у2 - 2ху + 2х - 2у < 0.
Задание 8.
Даны угол, стороны которого имеют уравнения у = 2х и у - 0, и точка А(4; 6), лежащая внутри этого угла. Точки В и С лежат на разных сторонах данного угла. Чему равно минимальное значение периметра треугольника ABC?
