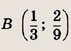Планиметрия

• Решение многих стандартных планиметрических задач «расчетного характера» опирается на знание основных понятий планиметрии и небольшое количество формул, связывающих между собой основные элементы геометрических фигур. Основой решения, как правило, является расчет того или иного треугольника. Пусть а, b, с — длины сторон АВС, лежащие соответственно против углов

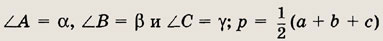
периметр АВС; S — площадь; R и r — радиусы описанной и вписанной окружностей; h_a, h_b , h_c — длинывысот, проведенных из вершин А, В и С.

Справедливы следующие равенства:

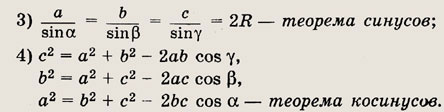
В частности, если

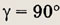
то АBС — прямоугольный. В этом случае теорема косинусов переходит в теорему Пифагора:

а² + b² = с².

При проведении вычислений в треугольнике следует смелее использовать тригонометрию. Применение тригонометрических формул к решению геометрических задач основано на следующих В соотношениях в прямоугольном треугольнике:

если

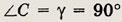
то

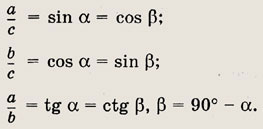
Напомним еще, что центр вписанной окружности совпадает с точкой пересечения биссектрис треугольника, а центр описанной окружности — с точкой пересечения перпендикуляров к серединам сторон. Другие сведения, необходимые для решения задач, мы будем напоминать в соответствующей части текста.

Решите следующие задачи (1—121):

Задание 1.

Длина одного из катетов прямоугольного треугольника больше длины другого катета на 10 см, но меньше длины гипотенузы на 10 см. Найдите длину гипотенузы.

Решение.

Пусть х см и у см — длины катетов треугольника (х > у). Согласно теореме Пифагора длина гипотенузы равна

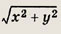
По условию

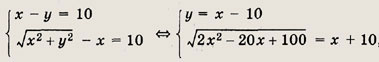
откуда

Ответ:

50 см.

Задание 2.

Сумма длин катетов прямоугольного треугольника равна 34 см, а разность их длин равна 14 см. Найдите длину гипотенузы.

Ответ:

26 см.

Задание 3.

Найдите отношение длины гипотенузы прямоугольного треугольника к длине большого катета, если:

а) длины катетов относятся как 3 : 7;
б) длины катетов относятся как

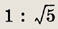
в) длина гипотенузы относится к длине меньшего катета как 3:1.

Решение.

а) Обозначим катеты через а = Зx и b = 7х. По теореме Пифагора гипотенуза

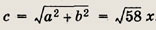
Отношение гипотенузы к большему катету

Ответ:

a)

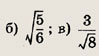
Задание 4.

В прямоугольном треугольнике один из углов равен 30°, а сумма длин гипотенузы и меньшего катета равна 9 см. Найдите длины гипотенузы и катетов.

Указание.

Гипотенуза в 2 раза больше меньшего катета.

Ответ:

Задание 5.

Длины сторон прямоугольного треугольника образуют арифметическую прогрессию. Найдите величины острых углов треугольника.

Решение.

Пусть а — первый член ее прогрессии, a d — ее разность. Тогда катеты и гипотенуза треугольника равны а, а + d и а + 2d.

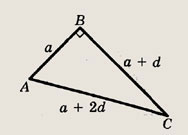
По теореме Пифагора

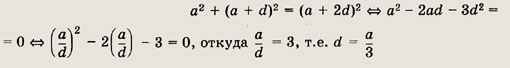
Таким образом,

Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе,
т.е.

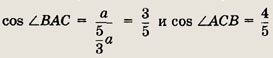
Ответ:

Задание 6.

Меньший катет прямоугольного треугольника равен а, длины его сторон образуют арифметическую прогрессию. Найдите площадь треугольника.

Ответ:

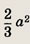
Задание 7.

В прямоугольном треугольнике длины медиан, проведенных к катетам, равны 4 см и 5 см. Найдите длину гипотенузы.

Ответ:

Задание 8.

Найдите длину высоты прямоугольного треугольника, если он делит гипотенузу на отрезки 32 см и 18 см.

Указание.

Пусть h — высота. Тогда квадраты катетов равны h² + 32² и h² + 18², квадрат гипотенузы равен 50².

Ответ:

24 см.

Задание 9.

Найдите острые углы прямоугольного треугольника, если медиана, проведенная к гипотенузе, делит прямой угол в отношении 1 : 2.

Ответ:

30°; 60°

Задание 10.

На гипотенузе прямоугольного треугольника взята точка, равноудаленная от обоих катетов. Эта точка делит гипотенузу на отрезки 30 см и 40 см. Найдите длины катетов.

Решение.

Пусть

Положим < BAC = < BDM = а. Так как

т.е

а катет

Ответ:

42см.; 56 см.

Задание 11.

В равнобедренный прямоугольный треугольник вписан квадрат так, что две его вершины лежат на гипотенузе, а две другие — на катетах. Найдите длину стороны квадрата, если длина гипотенузы равна 6 см.

Ответ:

2 см.

Задание 12.

В прямоугольном треугольнике один катет вдвое длиннее другого, в длина гипотенузы равна

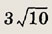
Найдите длину биссектрисы прямого угла.

Ответ:

4 см.

Задание 13.

В АBС внутренний угол при вершине А равен 72°, а внешний угол при вершине В равен 105°. Найдите остальные внутренние углы АBС:

Ответ:

72°; 75°; 33°

Задание 14.

В АBС из вершины B проведена биссектриса BL. Внешний угол при вершине B равен 70°, a < BAC = 30°. Найдите < BLC.

Ответ:

85°

Задание 15.

В АBС величина < BСА в 2 раза меньше разности углов < ABC и < BAC и в 5 раз меньше суммы этих углов. Найдите углы АBС.

Ответ:

105°; 45°; 30°

Задание 16.

В PQR < QPR = 75°, < PRQ = 40°. Найдите:

а) угол между высотами РК и QL;

б) угол между высотой РК и биссектрисой РМ.

Решение.

а) Пусть N — точка пересечения высот QL и РК.

Требуется найти угол < PNL. Треугольник PKR — прямоугольный, значит, сумма его острых углов равна < KPR + < KRP = 90°. Но < KRP = 40°, поэтому < KPR = 50°. Аналогично, из прямоугольного треугольника PLH находим угол < PNL = 90° - < LNPL = 90° - < KPR = = 40°.

Ответ:

a) 40°

б) 12,5°

Задание 17.

В PKС биссектрисы углов при вершинах Р и К пересекаются в точке О. Известно, что < РОK = 110°, < КСР в 3 раза меньше угла < KPC. Найдите углы ABС.

Решение.

Пусть KL и РМ — биссектрисы,

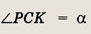
Тогда

Кроме того,

Запишем сумму углов PKC:

Ответ:

20°; 40°; 60°

Задание 18.

В АBС высоты, проведенные из вершин А и B, пересекаются в точке О. Известно, что < АОВ = 108°, а величина < BСА в 1,5 раза больше величины угла < АBС. Найдите углы АBС.

Ответ:

44°; 72°; 60°

Задание 19.

В равнобедренном треугольнике основание равно 30 см, а высота, опущенная на это основание, равна 20 см. Найдите длину высоты, опущенной на боковую сторону.

Ответ:

24 см.

Задание 20.

Найдите площадь равнобедренного треугольника, если высота, опущенная на основание, равна 10 см, а высота, опущенная на боковую сторону, равна 12 см.

Решение.

Пусть АВ = ВС, BD = 10 см, АH = 12 см.

Тогда площадь треугольника

С другой стороны,

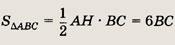
Таким образом,

Полагая АС = 6x и ВС = 5х, найдем

По теореме Пифагора из прямоугольного треугольника BDС высота

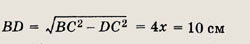
откуда

Ответ:

75 см².

Задание 21.

Основание равнобедренного треугольника равно

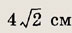
а медиана боковой стороны равна 5 см. Найдите длину боковой стороны.

Решение.

Пусть АВ = ВС, AM — медиана, О — точка пересечения медиан.

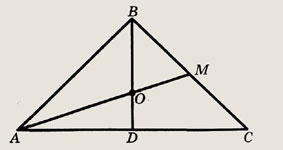
Так как

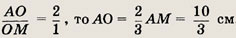
Аналогично,

откуда по теореме Пифагора

Сторону АВ находим по теореме Пифагора из прямоугольного треугольника ADB.

Ответ:

6 см.

Задание 22.

В треугольнике длина основания на 4 см меньше длины высоты, опущенной на это основание. Площадь треугольника равна 96 см². Найдите длину основания.

Ответ:

12см.

Задание 23.

Площадь равнобедренного треугольника АBС (АB = BС) равна 36 см², BD — высота. Найдите длину стороны

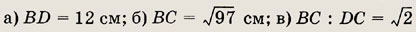
Решение.

б) Пусть DC = х.

По теореме Пифагора

Тогда площадь

Решив это уравнение, находим х₁ = 9, х₂ = 4. Так как х — половина искомой стороны, то получаем, что длина АС равна либо 8 см, либо 18 см.

Ответ:

а) 6 см.
б) 8 см или 18 см.
в) 12 см.

Задание 24.

В КLМ найдите длину высоты КР, если:

а) KL = 10 см, LM = б см, КМ = 8 см;

б) KL = 12 см, LM = 5 см, КМ = 9 см.

Ответ:

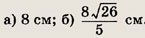
Задание 25.

В АBС стороны АВ и АС равны соответственно 3 см и 6 см. Длина высоты, опущенной из вершины А, равна полусумме длин высот, опущенных из вершин В и С. Найдите длину стороны ВС.

Ответ:

4 см.

Задание 26.

Найдите косинусы углов АВС, если:

а) АВ = 3 см, ВС = 4 см, АС = 5 см;

б) АВ = 12 см, ВС = 13 см, АС = 10 см;

в) АВ = 10 см, ВС =8 см, АС = 3 см.

Решение.

а) По теореме косинусов имеем АС² = ВС² + АВ² -- 2АВ • ВС cos < AВС, т.е.

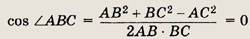
Аналогично,

Ответ:

a)

Задание 27.

В АВС найдите длину стороны АС, если:

Указание.

Обозначьте сторону АС через х и примените теорему косинусов. .

Ответ:

а) 12 см.
б) 4 см.

Задание 28.

В треугольнике длины сторон равны 11, 12 и 13 см. Найдите длину медианы, проведенной к большей стороне.

Ответ:

9,5 см.

Задание 29.

В треугольнике величины углов при вершинах относятся как 3 : 4 : 5, а длина стороны, лежащей против
меньшего угла, равна

Найдите длины сторон и площадь треугольника.

Ответ:

Задание 30.

В АВС известно, что АС = 5, АВ - ВС = 2 см, < BCA : < BAC = 2 : 1. Найдите длины сторон АВС.

Решение.

Пусть

(рис. а).

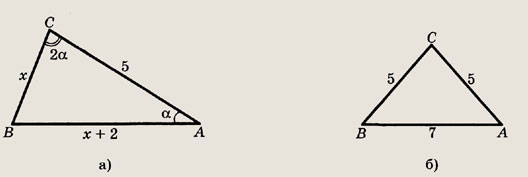
Тогда АВ = х + 2 и

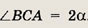
По теореме синусов

теореме косинусов

т.е.

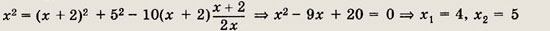
Корень x₂ не подходит. Действительно, используя теорему косинусов, найдем косинусы углов АВС (рис. б).

Ho

Ответ:

4 см.; 5см.; 6 см.

Задание 31.

В равнобедренном треугольнике угол при основании равен

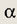
Найдите периметр треугольника, если его площадь равна S.

Ответ:

Задание 32.

В равнобедренном треугольнике ABC на боковой стороне ВС взяты точки D и Е так, что DE = ЕС = 2 см.
Найдите периметр АВС, если

Решение.

Пусть

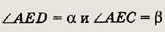
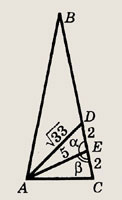
По теореме косинусов

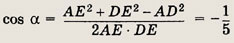
Так как

то

Далее, снова по теореме косинусов АС² = АE² + ЕС² - 2АЕ • ЕС cos ß = 25, т.е. АС = 5. Треугольник ЕАС — равнобедренный и, следовательно, < ACE = ß. Треугольники ABC и EАС подобны, причем коэффициент подобия равен

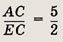
Отношение периметров подобных треугольников равно коэффициенту подобия, т.е.

Ответ:

30 см.

Задание 33.

Точка D лежит на боковой стороне ВС равнобедренного треугольника ABC. Найдите площадь АВС, если

Ответ:

 

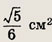
• Напомним, что площадь параллелограмма находится по формуле

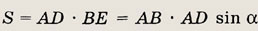
где BE -- высота, проведенная к стороне AD.

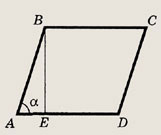
Площадь трапеции ABCD (AD || BC) вычисляется по формуле

где BE — высота, проведенная к основанию AD.

Задание 34.

Площадь прямоугольника равна

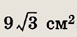
а величина одного из углов, образованного диагоналями, равна 120°. Найдите стороны прямоугольника.

Ответ:

Задание 35.

Найдите величину угла между диагоналями прямоугольника, если его периметр равен 2р, а площадь равна

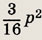
Ответ:

П - 2 arctg 3.

Задание 36.

Периметр прямоугольника равен 46 см, а его диагональ равна 17 см. Найдите площадь прямоугольника.

Ответ:

120см².

Задание 37.

Одна из сторон параллелограмма равна

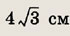
его площадь равна 12 см², а острый угол между сторонами равен 60°. Найдите длину другой стороны параллелограмма.

Ответ:

2 см.

Задание 38.

Найдите площадь параллелограмма, если его диагонали равны 3 см и 5 см, а острый угол между ними равен 60°.

Ответ:

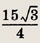
Задание 39.

Найдите площадь параллелограмма, если его диагонали равны 25 см и 15 см, а острый угол между сторонами равен 45°.

Ответ:

100 см²

Задание 40.

Периметр ромба равен 48 см, а сумма длин его диагоналей равна 26 см. Найдите площадь ромба.

Решение.

Пусть О — точка пересечения диагоналей ромба.

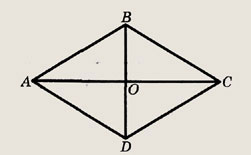
Стороны ромба равны, т.е. АВ = ВС = CD = AD = 12см. Пусть ОВ = х; тогда ОС = 13 - х. По теореме Пифагора х² + (13 - х)² = 12², 2x² - 26x + 25 = 0, т.е. 26x - 2x² = 25. Так как

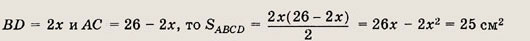
Ответ:

25 см²

Задание 41.

Сумма длин диагоналей ромба равна 5 см, а его площадь равна 2 см². Найдите длину стороны ромба.

Ответ:

Задание 42.

Найдите площадь ромба, если его высота равна 12 см, а меньшая диагональ равна 13 см.

Ответ:

202,8 см.

Задание 43.

Найдите длину стороны ромба, если его площадь равна Q, а длины диагоналей относятся как m : n.

Ответ:

Задание 44.

Длины сторон параллелограмма относятся как 5 : 8, угол между ними равен 60°. Найдите периметр параллелограмма, если его площадь равна

Ответ:

52 см.

Задание 45.

В параллелограмме ABCD АВ = 2 см, ВС = 3 см, точка Е — середина стороны AD. Найдите площадь параллелограмма, если известно, что отрезки АС и BE перпендикулярны.

Решение.

Проведем DM и C/V параллельно jB? (точка М лежит на ВС, N — на продолжении AD).

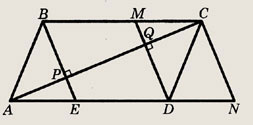
Пусть Р и Q — точки пересечения BE и MD с АС. Треугольники ABE и MCD равны (АВ = CD, < ВАЕ = < МСD и < ABE = < CDM как углы со взаимно параллельными и противоположно направленными сторонами). Отсюда следует, что

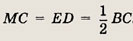
По теореме Фалеса, примененной к углам

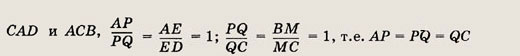
Обозначим эти отрезки через y.

Треугольники АРE и BРС подобны по трем углам, причем коэффициент подобия равен

Пусть РЕ = х, тогда ВР = 2x. Так как АBE = DCN (АВ = DC, BE = CN, < ABE = = < DCN), то S_ABCD = S_EBCN. Площадь параллелограмма EBCN равна CP • BE = 6xy. Следовательно, S_ABCD = 6xy. Из прямоугольных треугольников APB и ВРС получаем:

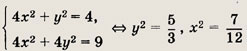
Таким образом,

Ответ:

Задание 46.

В равнобочной трапеции высота равна 12 см, а средняя линия равна 16 см. Найдите длину диагонали трапеции.

Решение.

Пусть MN — средняя линия трапеции, ВР и CQ — высоты.

Треугольники АВР и QCD равны по гипотенузе (AS = CD) и катету (ВР = CQ). Следовательно, АР = QD. Кроме того, ВС = PQ. Сумма оснований трапеции ВС + AD = ZAP + 2PQ = 2AQ. Отсюда следует, что AQ = MN = 16 см. Диагональ АС находим из прямоугольного треугольника

Ответ:

20 см.

Задание 47.

В равнобочной трапеции длина боковой стороны равна длине средней линии. Найдите длину боковой стороны, если периметр трапеции равен 48 см.

Ответ:

12 см.

Задание 48.

Средняя линия трапеции равна 10 см и делит ее площадь в отношении 3:5. Найдите длины оснований трапеции.

Ответ:

5 см и 15 см.

Задание 49.

На боковых сторонах АВ и CD трапеции ABCD взяты точки М и N так, что отрезок MN параллелен основаниям и делит площадь трапеции пополам. Найдите MN, если ВС = a, AD = b.

Решение.

Пусть ВС = a, AD = b.

Продолжим АВ и CD до пересечения в точке S. Треугольники ASD, MSN, BSC подобны. Площади подобных треугольников относятся как квадраты соответствующих сторон. Обозначим площадь треугольника BSC через

а длину MN — через х. Тогда

Так как

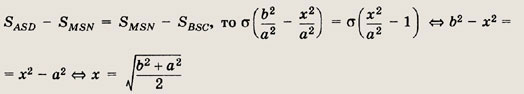
Ответ:

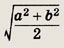
Задание 50.

Диагональ равнобочной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 3 см, а периметр равен 42 см. Найдите площадь трапеции.

Указание.

Проведите диагональ и докажите, что отсекаемый остроугольный треугольник является равнобедренным.

Ответ:

96 см²

Задание 51.

Основания трапеции равны 4 см и 10 см. Одна из боковых сторон составляет с меньшим основанием угол 150°. Найдите эту боковую сторону, если площадь трапеции равна 21 см².

Ответ:

6см.

Задание 52.

Основание АВ трапеции ABCD вдвое длиннее основания CD и боковой стороны AD. Найдите площадь трапеции, если АС = а, ВС = b.

Ответ:

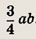
Задание 53.

Длины основания KN, диагонали КМ и боковой стороны KL трапеции KLMN равны а, а длина диагонали LN равна b. Найдите длину боковой стороны MN.

Решение.

Пусть LH и МР — высоты трапеции и пусть НК = х

По теореме Пифагора

Из прямоугольного треугольника LHN получаем

LH² + HN² = LN²<=> (а² - х²) + (а + х)² = b² <=> 2ах = b² - 2а².

Треугольники LHK и МРК равны как прямоугольные по катету и гипотенузе, поэтому КР = НК = х. В прямоугольном треугольнике MPN сторона

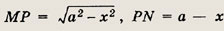
поэтому MN² = МР² + PN² = а² - х² + (а - х)² = 2а² - 2ах = 2а² - (b² - 2а²) = 4а² - b², т.е.

Ответ:

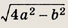
Задание 54.

Длина диагонали BD трапеции ABCD равна т, а длина боковой стороны AD равна n. Найдите длину основания CD, если известно, что длины основания, диагонали и боковой стороны трапеции, выходящих из вершины С, равны между собой.

Ответ:

Задание 55.

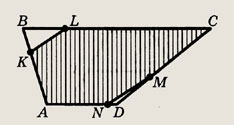
В выпуклом четырехугольнике ABCD диагонали АС и BD пересекаются в точке О. Найдите отношение площадей:

а) АВС и АBD, если АО : ОС = 3 : 4, ВО : OD = 2 : 5;

б) АОВ и ВОС, если АО : ОС = 3 : 5;

в) ВС.О и AOD, если АО : ОС = 1 : 2, ВО : OD = 3 : 1.

Решение.

а) Пусть S_boc = S.

Из того, что

Так как

Значит,

Ответ:

a) 2 : 3
б) 3 : 5
в) 8 : 3

Задание 56.

На сторонах выпуклого четырехугольника ABCD, площадь которого равна 1, взяты точки: К на АВ, L на ВС, М на CD и N на АD так, что АК : KB = 2; BL : LC = = 1 : 3; СМ : MD = 1; DN : NA = 1 : 5. Найдите площадь шестиугольника AKLCMN.

Решение.

Площади треугольников ABC и KBL

относятся как

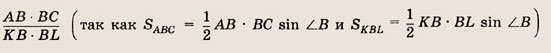
т.е.

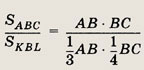
откуда

Аналогично,

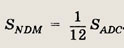
Площадь

Ответ:

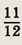
Задание 57.

Диагонали выпуклого четырехугольника ABCD пересекаются в точке Р. Известно, что площади АВР, ВСР и CDP равны соответственно S₁ S₂ и S₃. Найдите площадь ADP.

Ответ:

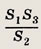
Задание 58.

Найдите площадь правильного двенадцатиугольника со стороной а.

• Радиусы, r и R вписанной в АВС и описанной около АВС окружностей вычисляются по формулам:

Указание.

Данный двенадцатиугольник можно разбить на 12 равнобедренных треугольников с боковой стороной а и углом 30° при вершине.

Ответ:

За²

Задание 59.

Найдите радиусы вписанной в АВС и описанной около АВС окружностей, если:

Ответ:

Задание 60.

В равнобедренном треугольнике сторона основания равна а, а радиус вписанной окружности равен r. Найдите длину боковой стороны треугольника.

Решение.

Положим

Пусть О — центр вписанной окружности.

Так как

то

Следовательно,

Ответ:

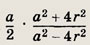
Задание 61.

Гипотенуза прямоугольного треугольника равна 34 см, а длины катетов относятся как 8 : 15. Найдите радиус вписанной окружности.

Ответ:

6 см.

Задание 62.

Периметр прямоугольного треугольника равен 2р (см), а его гипотенуза равна q (см). Найдите радиус вписанной окружности и площадь треугольника.

Решение.

Пусть вписанная окружность касается сторон АВС в точках P,Q, R.

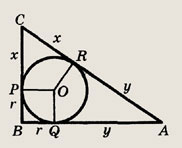
Тогда СР = CR, AR = AQ, BР = BQ как отрезки касательных, проведенных к окружности из одной точки. Положим CR = х, AR = у, ВР = r. (Заметим, что BPOQ — квадрат и r — радиус вписанной окружности.) Периметр АВС равен 2х + 2у + 2z = = 2р, но АС = х + у — гипотенуза, т.е. х + у = q. Таким образом, 2q + 2r = 2р <=> r = р - q к S_ABC - pr = р(р - q).

Ответ:

р - q ; р(р - q)

Задание 63.

Найдите радиусы вписанной в АВС и описанной около АBС окружностей, если длины сторон этого треугольника равны: а)10 см, 20 см, 24 см; б) 7 см, 5 см, 8 см; в) 13 см, 15 см, 20 см.

Указание.

Для нахождения площади треугольника примените формулу Герона.

Ответ:

и

 

Напомним, что площадь круга радиуса R вычисляется по формуле S = ПR².

Задание 64.

Найдите отношение площадей описанного около АВС и вписанного в АВС круга, если АВ = ВС = 6, < ABC = 120°.

Ответ:

Задание 65.

Стороны треугольника пропорциональны числам 3, 4 и 5. Во сколько раз площадь описанного около треугольника круга больше площади вписанного в него круга?

Ответ:

6 , 25

Задание 66.

В прямоугольном треугольнике гипотенуза равна 13 см, а катет равен 12 см. На какие отрезки делит точка касания вписанной окружности этот катет?

Ответ:

2 см и 10 см.

Задание 67.

В прямоугольный треугольник вписана окружность. Гипотенуза делится точкой касания в отношении 2:3. Найдите длину гипотенузы, если периметр треугольника равен 36 см.

Решение.

Пусть Р, Q, R — точки касания вписанной окружности со сторонами АВС.

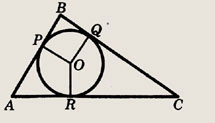
По условию,

Положим AR = 2х, RC = Зх, РВ = у. Так как АР = АR, СR = CQ, ВР = BQ, то АР = 2х, CQ = Зx, BQ = y. По теореме Пифагора АС² = АВ² + SC², т.е.

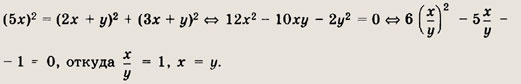
Таким образом, периметр АВС равен 5х + 4х + Зх = 12х = 36, откуда х = 3 и АС = 5х = 15.

Ответ:

15 см.

Задание 68.

В АВС < ACB = 90°, CD — высота, ВС = 3 см, АС = 4 см. Найдите расстояние между центрами окружностей, вписанных в CDB и ADC.

Указание.

Искомое расстояние можно найти по теореме Пифагора из прямоугольного треугольника О₁О₂Р

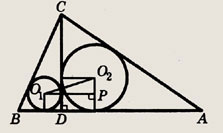
в котором О₁Р — сумма, а О₂Р — разность радиусов окружностей.

Ответ:

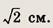
Задание 69.

В прямоугольном треугольнике ABC известны длины катетов: ВС = 4 см, АС = 3 см. Найдите расстояние между центрами вписанной в него и описанной около него окружностей. Где лежит центр описанной окружности?

Ответ:

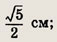
на середине гипотенузы.

Задание 70.

Катеты прямоугольного треугольника равны 15 см и 20 см. Найдите расстояние от центра вписанной в треугольник окружности до высоты, опущенной из вершины прямого угла.

Ответ:

1 см.

Задание 71.

В равнобедренном треугольнике основание равно 6 см, а боковая сторона равна 5 см. Найдите расстояние между центрами вписанной и описанной окружностей.

Ответ:

Задание 72.

В равнобедренном треугольнике центр вписанной окружности делит высоту треугольника в отношении 12 : 5. Найдите площадь этого треугольника, если длина боковой стороны равна 60 см.

Ответ:

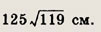
Задание 73.

В прямоугольный треугольник LMN вписана окружность радиуса а, касающаяся катета LN в точке Р. Длина катета LN равна 6а. Найдите длины сторон LMN и площадь PMN.

Указание.

Пусть Q — точка касания вписанной окружности катета LM. Положите QM = х и воспользуйтесь решением задачи 67.

Ответ:

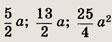
Задание 74.

В остроугольном треугольнике AВС величина угла при вершине А относится к величине угла при вершине С как 7:6. Найдите углы данного треугольника, если отрезок, соединяющий центры его вписанной и описанной окружностей, виден из вершины В под углом 5°.

Решение.

Пусть в АВС точка O₁ — центр вписанной, а О₂ — центр описанной окружности.

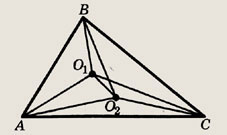
По условию отношение углов

Так как О₁ — центр вписанной окружности, то AO₁, BO₁, СО₁ — биссектрисы соответствующих углов АВС. Кроме того, отрезки О₂А, О₂В, О₂С равны, поэтому треугольники АО₂В, ВО₂С, АО₂С — равнобедренные и углы при основании у них равны. Таким образом,

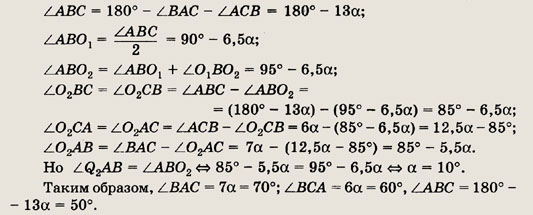
Ответ:

50°; 60°; 70°

Задание 75.

В остроугольном треугольнике ABC величина меньшего угла < ABC равна 40°, О -- центр описанной, К — центр вписанной окружности. Найдите углы АВС, если < OBK = 15°.

Ответ:

85°, 55°, 40°

Задание 76.

В остроугольном треугольнике ABC точка О — центр описанной окружности, длина наибольшей высоты BD равна 6 см, а величина наибольшего угла < BAC равна 80°. Найдите длину меньшей стороны треугольника, если < DBO = 10°.

Ответ:

6(tg 10° + tg 20°) см.

Задание 77.

В треугольнике ABC известны длины сторон: АВ = 21, ВС = 10 и АС = 17 см, О — центр вписанной в треугольник окружности. Эта окружность касается боковых сторон АВ и АС в точках М и N соответственно. Найдите площадь четырехугольника AMON.

Ответ:

49 см².

 

• В более сложных геометрических задачах часто бывает необходимо провести обоснование используемых соотношений между элементами фигур. Такое обоснование проводится с помощью теорем планиметрии. Приведем признаки подобия треугольников и некоторые следствия этих признаков, на которых основано решение многих последующих задач.

Два треугольника подобны, если выполнено хотя бы одно из следующих условий:

1) два угла одного треугольника соответственно равны двум углам другого треугольника;

2) длины двух сторон одного треугольника пропорциональны длинам двух сторон другого треугольника и углы, заключенные между этими сторонами, равны;

3) длины трех сторон одного треугольника пропорциональны длинам трех сторон другого треугольника.

В частности:

1) прямая, параллельная какой-либо стороне треугольника и пересекающая две другие его стороны, отсекает треугольник, подобный данному;

2) если длины гипотенузы и катета одного треугольника пропорциональны длинам гипотенузы и катета другого треугольника, то такие треугольники подобны.

Наконец, в подобных треугольниках все соответствующие линейные элементы, (высоты, медианы, биссектрисы, радиусы вписанной и описанной окружностей, периметры и т.д.) относятся как сходственные стороны, a площади подобных треугольников относятся как квадраты сходственных сторон.

Задание 78.

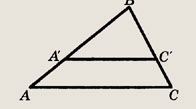
В АBС со сторонами АВ = 15 см, ВС = 17 см и АС = 10 см; проведен отрезок А'С' параллельно АС, причем точка А' лежит на АВ, а С' — на стороне ВС. Найдите:

а) ВС', если А'С' = 7;
б)А'В, если В'С' = 13;
в) А'С', если СС' = 3.

Решение.

а) Треугольник А'ВС' подобен треугольнику ABC

коэффициент подобия

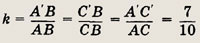
Таким образом,

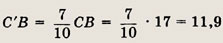
Ответ:

a)
11,9см.

Задание 79.

Катеты прямоугольного треугольника равны 7 см и 24 см. Найдите гипотенузу треугольника, подобного данному, если:

а) один из катетов равен 10 см;
б) разность катетов равна 51 см;
в) площадь равна 21 см².

Ответ:

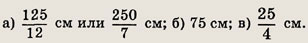
Задание 80.

В АВС проведены медиана BD и средняя линия DK, параллельная стороне АС. Площадь BDK равна 1. Найдите площадь АВС.

Ответ:

4

Задание 81.

В АВС со сторонами АВ = 15, ВС = 16 и АС = 9 через точку пересечения медиан проведены прямые, параллельные сторонам. Найдите площади отсекаемых треугольников.

Решение.

Площадь АВС найдем по формуле Герона:

Пусть О — точка пересечения медиан АВС.

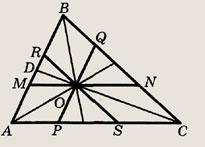
Проведем MN, PQ и RS параллельно сторонам. Требуется найти площади треугольников OQN, OPS, ORM.

Треугольники ABC и PQC подобны. Определим коэффициент подобия. По теореме Фалеса

значит, коэффициент подобия равен

Так как ON — средняя линия PQC, то OQN подобен PQC с коэффициентом подобия

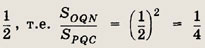
Окончательно получаем

Ответ:

Задание 82.

В прямоугольном треугольнике ABC из вершины прямого угла С проведена высота CD. Периметры ACD и DCB равны p и q соответственно. Найдите периметр АВС.

Ответ:

Задание 83.

В прямоугольном треугольнике ABC из вершины прямого угла С проведена высота CD. Радиусы окружностей, вписанных в АСD и DСВ, равны r₁ и г₁ соответственно. Найдите радиус окружности, вписанной в АВС.

Ответ:

Задание 84.

В АВС прямая, проходящая через вершину А, делит медиану BD пополам. В каком отношении эта прямая делит сторону ВС?

Решение.

Пусть М — середина BD.

Прямая AM пересекает ВС в точке N. Требуется найти отношение BN : NC. Проведем DK параллельно AN. Применив теорему Фалеса к углу DBC, получим

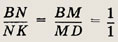
т.е. BN = NK. По той же теореме, применной к углу АСВ, имеем

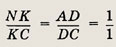
т.е. NK = КС. Значит,

Ответ:

1 : 2

Задание 85.

В АВС через середину медианы ВМ и точку D, лежащую на стороне ВС, проведена прямая. В каком отношении эта прямая делится медианой, если известно, что BD : DC = 3 : 2?

Решение.

Пусть N — середина ВМ, К — точка пересечения АВ и DN.

Требуется найти АК : КВ. Проведем СР и MQ параллельно KD и обозначим через R точку пересечения СР с ВМ. Применив теорему Фалеса к углу ABC (при параллельных KD и PC), получаем

Положим KB = Зх и КР = 2х. Аналогично находим

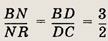
Пусть BN = Зу, NR = 2у. Так как ВМ = 2BN, то ВМ = 6y и AМ = у. По теореме Фалеса

откуда PQ = х. Отрезок QM — средняя линия АРС, поэтому AQ = QP = х и искомое отношение АК : KB = 4х : Зx = 4 : 3.

Ответ:

4:3

Задание 86.

В АВС точка К лежит на стороне АС и делит ее в отношении СК : КА = 1:3; точка М лежит на стороне ВС и делит ее в отношении СМ : MB = 2 : 5; D — точка пересечения отрезков AM и ВК. В каком отношении точка D делит отрезок AM?

Решение.

Требуется найти отношение AD : DM.

Используя условие, положим СК = х, КА = Зх, СМ = 2у, MB = 5y. Проведем MN параллельно ВК. По теореме Фалеса KN : NC = ВМ : МС = 5 : 2. Так как СК = х, то

Применив теорему Фалеса к углу MAC, получаем

Ответ:

21 : 5

Задание 87.

В &RPQ точка ./V делит сторону RQ в отношении RN : NQ = 2 : 7. Точка F делит RP в отношении RF : FP = 3:1. Прямые QF и PN пересекаются в точке М. Найдите длину MN, если РМ = 12.

Ответ:

28

Задание 88.

В АBС на стороне BС взята точка D так, что BD : DC = 3 : 5. Найдите отношение площадей АBD и АDС.

Указание.

Воспользуемся тем, что у треугольников ABD и DBC общая высота.

Ответ:

3 : 5

Задание 89.

В АBС на стороне ВС т АС взяты точки М и N так, что BМ : МС = 1 : 3, a AN : NC = 2 : 5. Найдите отношение площадей АBС и BMN.

Ответ:

28 : 5

Задание 90.

Точки F и N делят сторону АBС в отношении FA : FC = 3 : 1, CN : NB = 2 : 3. Прямые AN и BF пересекаются в точке М. Найдите отношение площадей АМБ и АNB.

Ответ:

5 : 6

Задание 91.

В АBС точка L делит пополам сторону BС, точка К делит пополам отрезок BL. На прямых АК и AL вне треугольника АBС отложены отрезки LD = AL и

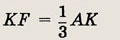
Найдите отношение площадей АБС и четырехугольника KLDF.

Указание.

Докажите, что

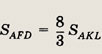
Ответ:

12 : 5

Задание 92.

В АBС точка М — середина стороны ВС, точка К лежит на стороне АС, причем АС = 4АК. Прямые AM и ВК пересекаются в точке О. Найдите длину МК, если известно, что AM = 5 см, ВК = 10 см, < AOB = 135°.

Указание.

Воспользуйтесь решением задачи 86 и найдите

Далее найдите длины отрезков ОВ и ОА и примените теорему косинусов.

Ответ:

Задание 93.

В АBС точка D — середина стороны АB, точка Е лежит на стороне BС, причем BС = ЗBЕ. Отрезки АЕ и CD пересекаются в точке О. Найдите АB, если известно, что АЕ = 5 см, ОС = 4 см, < АОС = 120°.

Ответ:

 

На свойстве биссектрисы, приведенном в задаче 94, основано решение следующих задач (94—109):

Задание 94.

В АBС биссектриса угла при вершине B пересекает сторону АС в точке D. Покажите, что AD : DC = АB : BС.

Решение.

Проведем высоту ВН

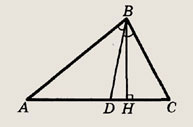
Это общая высота для треугольников ABD и DBC. Отношение

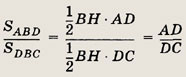
С другой стороны,

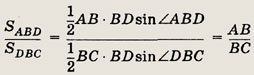
Таким образом,

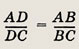
что и требовалось доказать.

Задание 95.

В АВС АС = 5, АВ = 6, BС = 7. Биссектриса угла С пересекает сторону АВ в точке D. Найдите площадь АDС.

Ответ:

Задание 96.

В АВС АВ = 4, BС = 6, < ABC = 30°. Биссектриса угла при вершине В пересекает сторону АС в точке D. Найдите площадь АВD.

Ответ:

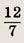
Задание 97.

В прямоугольном треугольнике ABC с прямым углом В биссектриса угла А пересекает сторону ВС в точке D. Известно, что BD = 4, DC = 6. Найдите площадь АDС.

Решение.

Используя результат задачи 94, получаем

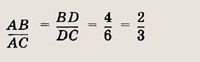
Положим АВ = 2х, АС = Зx. По теореме Пифагора

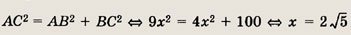
т.е.

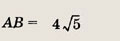
Площадь

то

Ответ:

Задание 98.

В АВС проведены биссектрисы BD и AF. Найдите отношение площадей АВС и CDF, если АВ = 6, ВС = 4 и АС = 3.

Ответ:

7,5

Задание 99.

В АВС биссектриса угла ВАС пересекает сторону ВС в точке М. Известно, что АВ = ВС = 2АС, AM = 4. Найдите площадь АВС.

Решение.

Пусть АС = х.

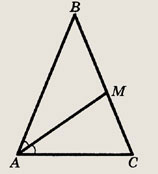
Тогда АВ = ВС = 2х. Значит,

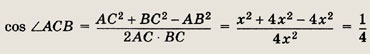
Поскольку

Применив теорему косинусов к АМС, получаем

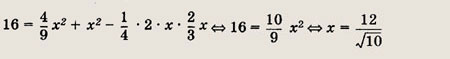
Учитывая, что

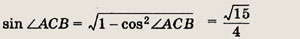
окончательно находим

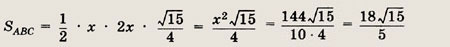
Ответ:

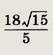
Задание 100.

В АВС биссектриса угла ABC пересекает сторону АС в точке К. Известно, что ВС = 2, КС = 1,

Найдите плошадь АВС.

Ответ:

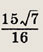
Задание 101.

Найдите косинус угла при вершине равнобедренного треутольника, если биссектриса угла при основании делит боковую сторону в отношении 3 : 2, считая от вершины.

Ответ:

Задание 102.

В АВС АС = 4 см, ВС = 3 см, ллощадь равна

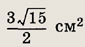
Медиана, проведенная к стороне АВ, меньше ее половины. Найдите длины отрезков, на которые сторона АВ делится биссектрисой.

Указание.

Медиана меньше половины стороны, к которой проведена, если треугольник тупоугольный. Это означает, что cos < АСВ < 0.

Ответ:

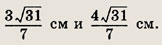
Задание 103.

Длина основания АС равнобедренного треугольника ABC равна 5 см, а длина биссектрисы АD равна 6 см. Найдите длину боковой стороны АВ.

Решение.

Пусть АВ = ВС = х.

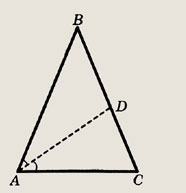
Тогда

то

Применив теорему косинусов к АОС, получим

Ответ:

20 см.

Задание 104.

В АВС угол ABC -- тупой, a < BAC = 45°. Биссектриса углаАСВ делит сторону АВ на отрезки AL = 8 см и BL = 6 см. Найдите радиус описанной окружности.

Ответ:

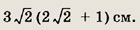
Задание 105.

Высота и биссектриса прямоугольного треугольника, опущенные из вершины прямого угла, равны 3 см и 4 см. Найдите площадь треугольника.

Решение.

Пусть BL и BD — биссектриса и высота прямоугольного треугольника ABC.

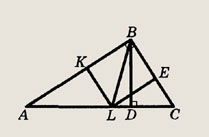
Опустим из точки L перпендикуляры LK и LE на АВ и BC. Так как BL — биссектриса, то KL = LE и KBEL — квадрат. Отсюда следует, что

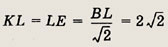
Пусть ВС = а, АВ = b. Тогда

С другой стороны,

Таким образом,

откуда

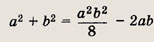
Кроме того,

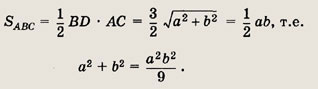
Приравняв правые части равенств получим аb = 144, следовательно,

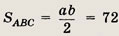
Ответ:

72 см²

Задание 106.

Угол А параллелограмма ABCD равен 60°. Вычислите площадь параллелограмма, если известно, что биссектриса угла А делит диагональ BD на отрезки, длины которых равны 1 см и 3 см.

Ответ:

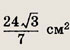
Задание 107.

В АBС ВС = АС = 12, АВ = 6, AD — биссектриса. Найдите радиус окружности, описанной около АDС.

Ответ:

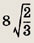
Задание 108.

В АBС АВ = 21, ВС = 15, BD — биссектриса. Найдите радиус окружности, вписанной в ABD, если

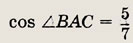
Решение.

Пусть АС = х.

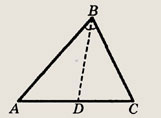
Применив теорему косинусов к AВС, получим

откуда x₁ = 12, Х₂ = 18.

1-й случай: АС = 12. По свойству биссектрисы

откуда АD = 7, DC = 5. Из

Так как

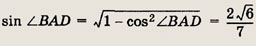
то

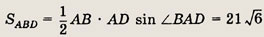
Периметр

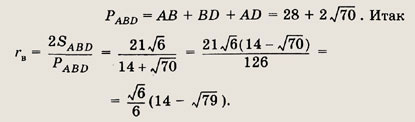
2-й случай: AC = 18. Этот случай рассматривается аналогично 1-му.

Ответ:

Задание 109.

В АВС проведена биссектриса ВК. Известно, что центр окружности, вписанной в АВК, совпадает с центром окружности, описанной около АВС. Найдите отношение длин сторон АВС.

Решение.

Пусть О — центр описанной около АВС окружности и одновременно — центр вписанной в АВК окружности.

Положим

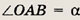
Треугольник АОВ — равнобедренный, поэтому

Так как ВО — биссектриса угла АВК, то

Далее ВК — биссектриса угла ABC, т.е.

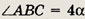
Значит,

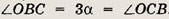
угол

поэтому

Сумма углов

откуда

По теореме синусов

и, поскольку sin 72° = 2 sin 36° cos 36°, sin 72° sin 72° sin36°, имеем

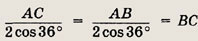
Ответ:

2cos 36° : 2cos 36° : 1

 

В задачах, связанных с высотами треугольника, часто используется свойство подобия треугольников, отсекаемых высотами, сформулированное в задаче 110.

Задание 110.

В остроугольном треугольнике АБС проведены высоты АЕ и CD. Докажите, что:

Решение.

б) Построим окружность с центром в середине отрезка

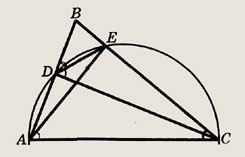
Эта окружность проходит через точки D и Е (углы < ADC и АЕС — прямые и опираются на диаметр).

Углы < CDE и < LCAE равны как вписанные и опирающиеся на одну дугу. Эти углы дополняют до 90° углы < BDE и < ACE соответственно, поэтому два последних угла также равны. Аналогично, < ВАС = < DEB и треугольники DBE и ABC подобны по трем углам. Коэффициент подобия равен отношению

(из прямоугольного треугольника BDC), что и требовалось доказать.

 

Используя утверждение задачи 110, решите следующие задачи (111—121):

Задание 111.

В остроугольном треугольнике АBС проведены высоты АЕ и CD. Найдите АВ, если BD = 18, BС = 30, АЕ = 20.

Ответ:

25

Задание 112.

В остроугольном треугольнике АBС проведены высоты СС₁ и AA₁. Известно что плошадь АBС равна 1,

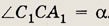
Найдите площадь С₁BA₁

Ответ:

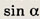
Задание 113.

В остроугольном треугольнике АБС проведены высоты СН и АН₁. Известно, что АС = 2 и площадь круга,
описанного около

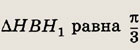
Найдите угол между высотой СН и стороной ВС.

Решение.

Пусть угол ABC = а.

Как следует из решения задачи 110 б, треугольники НВН₁ и ABC подобны и коэффициент подобия равен cos .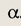

Таким образом,

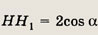
Радиус описанного около НВН₁, круга равен

Площадь круга равна

Искомый угол < HCB = 90° - а = 30°.

Ответ:

30°

Задание 114.

В остроугольном треугольнике ABC проведены высоты АР и CQ. Периметр АВС равен 15, периметр BPQ равен 9, а радиус описанной около BPQ окружности равен 9/5 . Найдите длину АС.

Ответ:

Задание 115.

В остроугольном треугольнике ABC проведены высоты АР и CQ. Площадь АВС равна 18, площадь PBQ равна 2,

Найдите радиус описанной около АВС окружности.

Ответ:

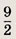
Задание 116.

В остроугольном треугольнике ABC проведены высоты АР и CQ. Найдите площадь четырехугольника AQPC, если АС = 6, площадь BPQ равна 1, а радиус описанной около АВС окружности равен

Ответ:

8

Задание 117.

В АВС АВ = BС = 6. На стороне АВ как на диаметре построена окружность, пересекающая ВС в точке D так, что BD : DC = 2 : 1. Найдите длину стороны АС.

Ответ:

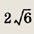
Задание 118.

В АВС известно, что АВ = 1. На стороне АВ как на диаметре построена окружность, делящая АС точкой D пополам, а сторону ВС точкой Е в отношении BE : ЕС = 7 : 2. Найдите длину стороны АС.

Ответ:

Задание 119.

В АВС на стороне АВ как на диаметре построена окружность, пересекающая стороны АС и ВС в точках D и Е соответственно. Прямая DE делит площадь АВС пополам и образует с прямой АВ угол 15°. Найдите углы АВС.

Ответ:

45°; 60°; 75°

Задание 120.

В АВС, углы которого образуют арифметическую прогресию с разностью 15°, проведены высоты AN, ВР и СМ. Найдите площадь MNP, если площадь АВС равна 1.

Указание.

Площади MBN, NCP и AМР равны cos² < MNB, cos² < NCP и cos² < MAP соответственно.

Ответ:

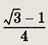
Задание 121.

Основания высот остроугольного треугольника ABC служат вершинами другого треугольника, периметр которого равен 2р. Найдите площадь АBС, если радиус описанной около него окружности равен R.

Указание.

Пусть AM, BN и СК — высоты АВС, О — центр описанной окружности. Покажите, что отрезок ОВ перпендикулярен стороне KM MNK

Для этого покажите, что < BAC = < BMK (см. задачу 110), а затем найдите < OMB (см. задачу 76 и близкие к ней задачи). Подсчет даст: < OMB = 90° -- < ABC. Аналогичный результат получится и для двух других вершин. Теперь, соединяя точку О с вершинами M4NK, найдите искомую площадь АВС.

Ответ:

pR

 

• Напомним: во всякий треугольник можно вписать окружность, вокруг всякого треугольника можно описать окружность. Центр вписанной окружности совпадает с точкой пересечения биссектрис данного треугольника, центр описанной окружности -- с точкой пересечения серединных перпендикуляров. Радиусы r и R вписанной и описанной окружностей находятся по формулам:

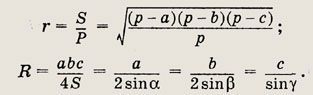
Длина L окружности радиуса R и площадь S ограничивающего ее круга вычисляются по формулам

L = 2ПR, S = ПR².

Сформулируем в виде задач некоторые хорошо известные утверждения, на которые опирается решение широкого круга задач с окружностями (122—130):

Задание 122.

Докажите, что радиус окружности, проведенной в точку касания, перпендикулярен касательной.

Задание 123.

Окружность касается сторон угла. Докажите, что ее центр лежит на биссектрисе этого угла.

Задание 124.

Из точки вне окружности проведены к ней две касательные. Докажите, что длины этих касательных равны.

Задание 125.

Докажите, что угол между касательной и хордой окружности, проведенной из точки касания, измеряется половиной дуги, стягиваемой этой хордой.

Задание 126.

Докажите, что вписанный в окружность угол измеряется половиной дуги окружности, на которую он опирается.

Задание 127.

Из точки А, лежащей вне окружности, проведены к этой окружности касательная АВ и секущая, пересекающая окружность в точках С и D, считая от точки А. Докажите, что

АВ² = АС • AD.

Решение.

Согласно результату задач 125 и 126 < CBA = < BDA.

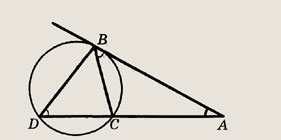
Значит, у треугольников ABD и ABC углы соответственно равны и эти треугольники подобны. Следовательно, равны и отношения сторон

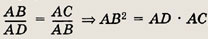
что и требовалось доказать.

Задание 128.

Докажите, что в остроугольном треугольнике центр описанной окружности лежит внутри треугольника, в тупоугольном — вне треугольника, а в прямоугольном треугольнике — на середине гипотенузы этого треугольника.

В отличие от треугольника многоугольники с большим числом сторон не всегда могут быть вписаны в окружность и описаны, вокруг окружности.

Задание 129.

Докажите, что около выпуклого четырехугольника можно описать окружность в том и только том случае, если сумма противоположных углов этого четырехугольника равна 180°. В частности:

а) около параллелограмма можно описать окружность в том и только том случае, если он прямоугольник;
б) около трапеции можно описать окружность в том и только том случае, если она равнобочная.

Задание 130.

Докажите, что в выпуклый четырехугольник можно вписать окружность в том и только том случае, если суммы длин противоположных сторон этого многоугольника равны. В частности, в параллелограмм можно вписать окружность в том и только том случае, если он ромб.

Указание.

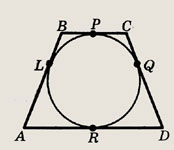
Пусть ВР = х, PC = у, DQ = z, AR = t. Тогда BL = х, CQ = у, DR = z, AL = t. Выразите суммы длин ВС + AD и AB + CD через введенные неизвестные.

 

Решите следующие задачи (131—186):

Задание 131.

На хорду АВ из центра круга опущен перпендикуляр ОС. Найдите:

а) радиус круга, если АВ = 6 см, ОС = 4 см;
б) хорды АВ, если ОС =12 см, а радиус круга 13 см.

Ответ:

а) 5 см; б) 10 см.

Задание 132.

Из точки А к окружности проведены две касательные АВ и АС. Найдите длину хорды ВС, если АВ = 12 см, а радиус окружности равен 10 см.

Ответ:

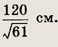
Задание 133.

К окружности проведены касательная АВ и секущая, пересекающая окружность в точках С и D (АС > AD). Найдите длину CD, если:

а) АВ = 12 см, АС = 18 см;
б) АВ = 15 см, AD = 9 см.

Ответ:

а) 10 см; б) 16 см.

Задание 134.

Найдите острый угол между касательной и хордой, проведенной из точки касания, если хорда делит окружность в отношении 2 : 7.

Ответ:

40°

Задание 135.

Окружность разделена точками на три части, относящиеся как 5 : 6 : 7. Через тючки деления проведены касательные. Определите углы треугольника, образованного этими касательными.

Ответ:

80°; 40°; 60°

Задание 136.

Концы диаметра окружности удалены от касательной на 12 см и 18 см. Найдите длину диаметра.

Решение.

Пусть A и В — концы диаметра, О — центр окружности и СQ — касательная.

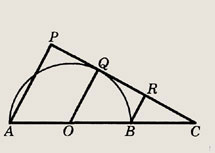
Опустим из точек А и В перпендикуляры АР и BR на касательн yю CQ. Треугольники АРС и BRC подобны, причем коэффициент подобия равен

поэтому

Пусть радиус полукруга равен r. Тогда АВ = 2r, ВС = 2АВ = 4r, ОС = 5r. Треугольники OQC и ВRС подобны. Коэффициент подобия равен

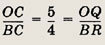
т.е.

Ответ:

15 см.

Задание 137.

Точка лежит внутри круга радиуса 6 см и делит проходящую через нее хорду на отрезки 5 см и 4 см. Найдите расстояние от этой точки до центра окружности.

Указание.

Через данную точку проведите диаметр. Обозначьте через х искомое расстояние и примените теорему о произведении отрезков пересекающихся хорд.

Ответ:

2 см.

Задание 138.

Точка лежит вне круга на расстоянии диаметра от его цента. Найдите угол между касательными, проведенными из этой точки к данному кругу.

Ответ:

60°

Задание 139.

Две окружности пересекаются в точках А и В. Прямая пересекает отрезок АВ, а также данные окружности последовательно в точках Р, Q, R и L. Величина

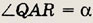
Найдите < PBL.

Решение.

Углы < BPR и < BAR равны как вписанные и опирающиеся на одну дугу.

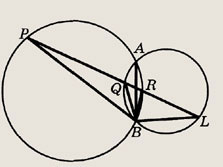
Аналогично, < QAB = < QLB. Но < QAB + < EAR = а, поэтому < BPL + < PLB = а, а искомый угол дополняет эту сумму до 180°.

Ответ:

Задание 140.

Найдите угол между двумя хордами, если точка их пересечения удалена от центра окружности на

и делит одну из хорд пополам, а другую в отношении 4 : 9.

Решение.

Пусть АР = РВ и СР : PD = 4 : 9.

Треугольники АОР и ОРВ равны по трем сторонам, поэтому < АРО = < OPE = 90°. Согласно теореме Пифагора

Положим СР = 4x и PD = 9х. По теореме о произведении отрезков пересекающихся хорд

откyда

Ответ:

Задание 141.

Точка Р удалена от центра окружности радиуса 11 на расстояние 7. Через эту точку проведена хорда длины 18. Найдите отношение длин отрезков, на которые точка Р делит хорду.

Ответ:

2

Задание 142.

Два кольца между тремя концентрическими окружностями равновелики. Радиус большей окружности равен 3 см, радиус меньшей окружности равен 1 см. Найдите радиус средней окружности.

Ответ:

Задание 143.

Из одной точки вне окружности проведены к этой окружности касательная и секущая наибольшей длины. Угол между ними равен arcsin 0,8. Найдите длину секущей, если радиус окружности равен 8 см.

Решение.

Секущая наибольшей длины проходит через центр круга. Докажем это. Пусть АС — секущая, проходящая через центр круга и AM — другая секущая.

Так как < AMC = < CMD + < DMA = 90° + < DMA, то AMC — тупоугольный, причем сторона АС лежит против тупого угла, т.е. АС > AM, что и требовалось доказать.

Пусть АВ — касательная. Тогда АОВ — прямоугольный. Гипотенуза

Ответ:

18 см.

Задание 144.

Из внешней точки проведены к окружности секущая длиной 12 см и касательная, составляющая

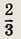
внутреннего отрезка секущей. Найдите длину касательной.

Ответ:

6 см.

Задание 145.

В окружности радиуса R = 4 см проведены хорда АВ и диаметр АК, образующий с хордой угол величиной

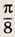
Через точку B к окружности проведена касательная, пересекающая продолжение АК в точке С. Найдите длину медианы AM ABC.

Решение.

Так как АВК — прямоугольный

то

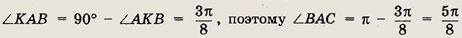
Угол АКB — вписанный и опирается на дугу АВ, следовательно,

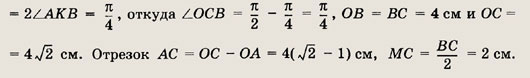
Применив теорему косинусов к АСМ, получаем

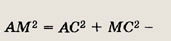
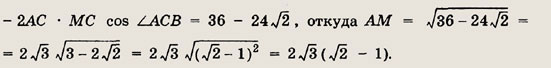
Ответ:

Задание 146.

В окружности радиуса

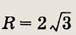
проведены хорда АВ и диаметр АК. Через точку В к окружности проведена касательная, пересекающая прямую АК в точке С (АС < АК) под углом 60° к АК. Найдите длину медианы AM АВС.

Ответ:

Задание 147.

Расстояние между центрами окружностей радиусов 1 см и 2 см равно 5 см. Найдите длину той их общей касательной, от которой центры окружностей лежат по разные стороны.

Решение.

Пусть O₁ и О₂ — центры окружностей радиуса 2 см и 1 см., А и В — точки касания общей касательной

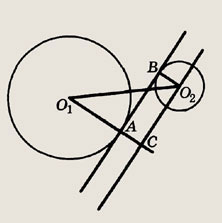
Через О₂ проведем прямую, параллельную АВ, которая пересекает продолжение О₁А в точке С. Треугольник О₁СО₂ — прямоугольный, причем O₁O₂ = 5 см и O₁C = 3 см. По теореме Пифагора О₂С = 4 см; так как АВО₂С — прямоугольник, то АВ = О₂С = 4 см.

Ответ:

4 см.

Задание 148.

Окружности радиусов 1 см и 3 см касаются внешним образом. Найдите длину той их общей касательной, от которой центры окружности лежат по одну сторону.

Ответ:

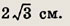
Задание 149.

Две окружности касаются друг друга внешним образом в точке С. Радиусы окружностей равны 2 см и 7 см. Общая касательная к обеим окружностям, проведенная через точку С, пересекается с другой их общей касательной в точке D. Найдите расстояние от центра меньшей окружности до точки D.

Решение.

Докажем, что O₁DO₂ — прямоугольный.

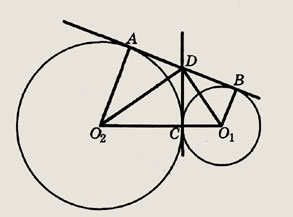
Пусть А и В — точки касания. Треугольники DCO₁ и DBO₁ равны по гипотенузе и катету, поэтому < EDO₁ = < CDO₁ Аналогично, < AO₂D = < DO₂C. Так как углы < O₂DC и < CDO₁ являются половинами углов < АDC и < СDВ, которые в сумме составляют 180°, то < O₂DC + < CDO₁ = < О₂DО₁ = 90°. Отрезок CD — высота в прямоугольном треугольнике O₂DO, значит, DC₂ = О₂С • СО₁ = 14, откуда

Ответ:

Задание 150.

Окружность радиуса 9 см касается внешним образом другой окружности в точке М. Общая касательная к обеим окружностям, проведенная через точку М, пересекается с другой их общей касательной в точке N. Найдите радиус второй окружности, если MN = 6 см.

Ответ:

4 см.

Задание 151.

Две окружности радиуса 32 см с центрами в точках О₁ и О₂, пересекаясь, делят отрезов О₁О₁ на три равные части. Найдите радиус окружности, которая касается изнутри обеих окружностей и отрезка О₁О₁.

Решение.

Пусть третья окружность касается первых двух в точках А и В, а прямой O₁O₂ — в точке С; М и N — точки пересечения первых двух окружностей с окружностью О,О₂.

Так как

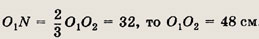
Из равенства треугольников O₁CO и О₂СО (по гипотенузе и катету) следует, что O₁C = = О₂С = 24 см.

Обозначим через r искомый радиус. В ОСО₂ имеем ОО₂ = 32 - r, ОС = r, О2С = 24 см, откуда (32 - r)² = r² + 24r² => r = 7.

Ответ:

7 см.

Задание 152.

Окружности радиусов R и г касаются друг друга внешним образом. Найдите радиус окружности, которая касается двух данных окружностей и их общей касательной.

Ответ:

Задание 153.

Три окружности одинакового радиуса 1 см касаются друг друга. Найдите радиус окружности, которой данные окружности касаются внутренним образом.

Ответ:

Задание 154.

В угол величины

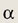
вписаны две касающиеся друг друга и сторон угла окружности. Найдите отношение радиусов этих окружностей.

Решение.

Пусть O₁ и О₁ — центры окружностей, А, В, С, D — точки касания окружностей сторон угла.

Радиусы окружностей обозначим через r и R. Проведем отрезок АР параллельно O₁O₂.

Так как ОО₁ — биссектриса угла

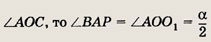
В прямоугольном треугольнике АВР имеем АР = O₁O₂ = r + R и BР = О₂В - О₂Р = О₂В - O₁A - R - r.

Следовательно,

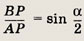
откуда

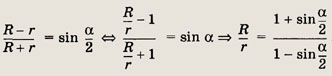
Ответ:

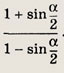
Задание 155.

Через концы дуги, содержащей 120°, проведены касательные и в фигуру, ограниченную этими касательными и данной дугой, вписана окружность радиуса 1 см. Найдите радиус исходной окружности.

Ответ:

3 см.

Задание 156.

Две окружности касаются друг друга внутренним образом в точке К. Через точку К проведен диаметр KD большей окружности. Хорда BD большей окружности касается меньшей окружности в точке С. Найдите длину CD, если

Решение.

Пусть О — центр меньшей окружности.

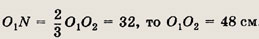
Треугольники BKD и ВОС подобны (они прямоугольные, так как < BDK — вписанный и опирается на диаметр, а ОС — радиус, проведенный в точку касания; кроме того, у этих треугольников общий острый угол). Отсюда следует, что

Радиус меньшей окружности обозначим через r. Поскольку

Искомый отрезок

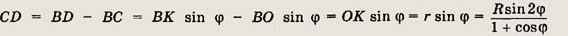
Ответ:

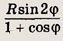
Задание 157.

На плоскости дан угол величиной

Окружность радиуса 2 см касается сторон этого угла. Найдите площадь фигуры, лежащей внутри угла, но вне окружности.

Указание.

Длина касательной равна

Ответ:

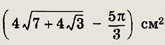
Задание 158.

На плоскости дан угол, равный

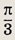
Окружность радиуса

касается одной стороны угла, а центр ее лежит на другой стороне. Найдите площадь криволинейного треугольника, расположенного внутри угла, но вне окружности.

Ответ:

Задание 159.

Расстояние между центрами двух кругов радиуса

Найдите площадь общей части этих кругов.

Ответ:

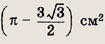
Задание 160.

В ромб, сторона которого равна 20 см, вписан круг. Найдите площадь круга, если одна диагональ ромба
4 больше другой в

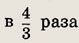
Ответ:

92,16 П см²

Задание 161.

Тупой угол ромба в 5 раз больше его острого угла. Во сколько раз сторона ромба больше радиуса вписанной окружности?

Ответ:

4см.

Задание 162.

Площадь круга, вписанного в ромб, в два раза меньше площади ромба. Найдите величину острого угла ромба.

Указание.

Пусть

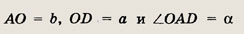
Выразите через эти величины площади круга и ромба.

Ответ:

Задание 163.

Найдите площадь ромба ABCD, если радиусы окружностей, описанных около АВС и АBD, равны R и r.

Решение.

Пусть

учитывая, что

то

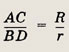
Пусть сторона ромба BС = а; тогда его диагонали

Ответ:

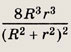
Задание 164.

Сторона ромба ABCD равна 6. Расстояние между центрами окружностей, описанных около АВС и ABD, равно 8. Найдите радиусы этих окружностей.

Ответ:

Задание 165.

Три последовательные стороны описанного около круга четырехугольника относятся как 3 : 4 : 5, а периметр этого четырехугольника равен 48 см. Найдите длины его сторон.

Ответ:

9 см; 12 см; 15 см; 12 см.

Задание 166.

В АВС вписана окружность, касающаяся стороны ВС в точке D. Найдите длину АС, если известно, что

Решение.

Обозначим точки касания вписанной окружности со сторонами треугольника через D, Р и Q.

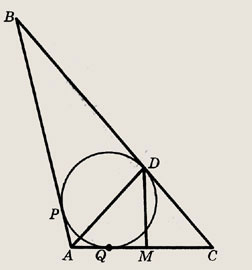
Пусть DC = х, тогда BD = 9 - х. Отрезки CD = CQ, АР = AQ и ВР = BD как касательные, проведенные к окружности из одной точки. Опустим высоту DM в АОС. Тогда

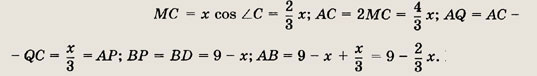
Применив теорему косинусов к АВС, получаем

Ответ:

4

Задание 167.

В АВС вписана окружность, касающаяся стороны ВС в точке D. Найдите длину АС, если известно, что

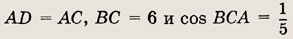
Ответ:

5

Задание 168.

В равнобочную трапецию вписана окружность радиуса 2 см. Найдите площадь трапеции, если длина ее боковой стороны равна 10 см.

Ответ:

40 см²

Задание 169.

В равнобочную трапецию, основания которой равны 8 см и 2 см, вписана окружность. Найдите длину этой окружности.

Ответ:

4П см

Задание 170.

Вершины прямоугольника, вписанного в окружность, делят ее на четыре дуги. Найдите расстояние от середины одной из больших дуг до ближайшей вершины прямоугольника, если его стороны равны 24 см и 7 см.

Ответ:

15 см.

Задание 171.

Около прямоугольника ABCD описана окружность, на которой взята точка М, равноудаленная от вершин А и В. Отрезки МС и АВ пересекаются в точке Е. Найдите площадь четырехугольника АМВС, если ME — = 2 см и ЕС = 16 см.

Решение.

Проведем прямую МК перпендикулярно АВ, которая пересечет АВ и CD в точках Р и Q

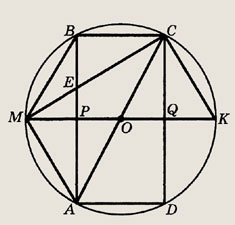
Треугольники МРВ и МРА равны как прямоугольные по гипотенузе и катету, поэтому АР = РВ. Таким образом, МК перпендикулярна хорде АВ и проходит через ее середину, т.е. МК — диаметр окружности;

AC — также диаметр, поскольку центр окружности, описанной около прямоугольника, лежит на его диагонали. Треугольники МЕР и ВСЕ подобны с коэффициентом подобия

Пусть МР = х, тогда ВС = PQ = 8x и МК = Юx. По теореме Пифагора

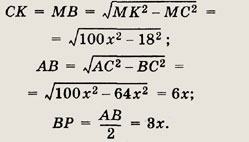
Из MPB по теореме Пифагора

Искомая площадь

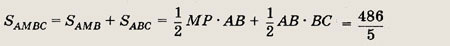
Ответ:

97,2 см²

Задание 172.

Окружность с центром в точке Р касается диагонали АС прямоугольника ABCD и продолжений сторон ВС и AD. Прямая CD делит отрезок АР на части 6 см и 2 см, считая от вершины А; К — точка касания окружности и прямой AD. Найдите площадь четырехугольника АМВС.

Ответ:

25,6 см²

Задание 173.

Равнобедренный треугольник ABC (АВ = ВС) вписан в окружность с центром К. Из вершины А проведен диаметр АР. Отрезки ВР и АС пересекаются в точке Е, причем BE = 2,25 см, ЕР = 6,75 см. Найдите периметр четырехугольника АВСР.

Ответ:

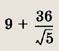
Задание 174.

В АВС, где АВ = 10, ВС = 20 и < ACB = 30°, вписана окружность. Через точку М на AC (AM = 10) проведена касательная к окружности; К — точка пересечения касательной с прямой, проходящей через точку B параллельно стороне АС. Найдите площадь четырехугольника АВKМ.

Ответ:

Задание 175.

В окружность вписан равнобедренный треугольник ABC, где АВ = ВС и < ABC = ß. Средняя линия треугольника, параллельная стороне АС, продолжена до пересечения с окружностью в точках D и Е. Найдите отношение площадей АВС и DBE.

Ответ:

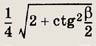
Задание 176.

Радиус окружности, вписанной в АВС, равен 1. Другая окружность касается стороны АС и продолжений сторон АВ и ЕС. Во сколько раз периметр АВС превосходит длину стороны АС, если радиус второй окружности равен 3?

Решение.

Пусть Р, Q, R, К, N, M — точки касания.

Положим ВР = BQ = х, CQ = RC = у, АК = AM = u, CN = СМ = v, АР = AR = z.

Точки О₂, O₁ В лежат на одной прямой. Треугольники О₁Q В и O₂NB подобны с коэффициентом подобия

,

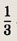поэтому 3BQ = BN => Зx = x + у + u <=> 2х - у + о. Аналогично, 2х = u + z. Сложив два последних равенства, получим 4x = u + z + y + v, т.е. 2х = АС. Периметр треугольника ABC равен АВ + ВС + АС = z + х + x + y + u + v = 6x = ЗАС.

Ответ:

3

Задание 177.

В АВС АВ = 10, ВС = 17 и АС = 21. Окружность касается продолжений сторон АВ и АС в точках М и N и стороны ВС. Найдите площадь AMN.

Ответ:

230,4

Задание 178.

Окружность радиуса 3 вписана в АВС и касается стороны ВС в точке D. Другая окружность радиуса 4 касается продолжения сторон АС и АВ, а также стороны ВС в точке Е. Найдите длину ED, если < BCA = 120°.

Ответ:

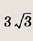
Задание 179.

Около прямоугольного треугольника описана окружность. Другая окружность того же радиуса касается катетов этого треугольника, причем одной из точек касания является вершина треугольника. Найдите отношение площади треугольника к площади общей части этих кругов.

Ответ:

Задание 180.

В прямоугольном треугольнике ABC из вершины прямого угла С проведена медиана CD. Найдите расстояние между центрами окружностей, вписанных в ACD и BCD, если ВС = 4, а радиус окружности, описанной около АВС, равен 2,5.

Указание.

Найдите стороны треугольника ABC

Затем найдите радиусы окружностей по формуле

где S — площадь треугольника, а р— полупериметр. Отрезки ВР и AQ можно вычислить по формулам

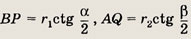
Искомый отрезок O₁O₂ определите по теореме Пифагора из прямоугольного треугольника O₁RO₂.

Ответ:

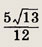
Задание 181.

В острые углы прямоугольного треугольника вписаны две равные окружности, касающиеся друг друга. Известно, что сумма площадей соответствующих кругов равна площади вписанного в данный треугольник круга. Найдите острые углы треугольника.

Ответ:

45° и 45°

Задание 182.

В прямоугольном треугольнике ABC из вершины прямого угла проведена высота CD. Найдите радиус вписанного в АВС круга, если радиусы кругов, вписанных в АСD и BCD, равны r₁ и r₂.

Ответ:

Задание 183.

В АВС вписана окружность, к которой проведены касательные, параллельные сторонам треугольника. Радиусы окружностей, вписанных в образовавшиеся треугольники, равны r₁, r₂ и r₃. Найдите радиус окружности, вписанной в АBС.

Решение.

Пусть r — радиус вписанной в АВС окружности. Продолжим MN и RT до пересечения в точке А'

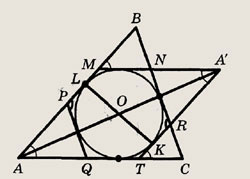
Треугольники APQ и A'NR подобны по трем углам. Из равенства треугольников OLA и ОКА' следует равенство отрезков А'К и AL. Аналогично можно показать, что PL = KR и, следовательно, АР = A'R. Это означает, что треугольники APQ и A'NR равны. Треугольники ABC, APQ, MBN и CRT подобны, причем радиусы вписанных окружностей этих треугольников пропорциональны соответствующим сторонам, т.е

Обозначим эти отношения через t. Тогда r₁ = t • PQ, r₂ = t • BN; r₃ = t • RC, t = t • ВС. Но PQ + BN + RC = ВС (так как PQ = NR), поэтому r₁ + r₂ + r₃ = r.

Ответ:

r₁ + r₂ + r₃ = r

Задание 184.

В АBС вписана окружность, к которой проведены касательные, параллельные сторонам треугольника. Площади образовавшихся треугольников равны S₁ , S₂ и S₃. Найдите площадь данного треугольника.

Ответ:

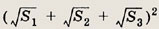
Задание 185.

Окружности радиусов R и r касаются друг друга внешним образом, AD (A # D) и ВС (В # С) — общие касательные к этим окружностям. Покажите, что в четырехугольник ABCD можно вписать окружность, и найдите ее радиус.

Указание.

Докажите, что OD, ОА, ОВ и ОС являются биссектрисами углов CDA, DAB, ABC и BCD

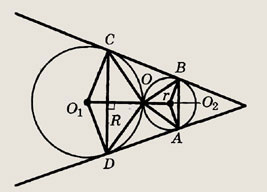
и, значит, точка О равноудалена от сторон трапеции ABCD.

Ответ:

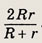
Задание 186.

Найдите расстояние между центрами вписанной в АBС и описанной около АBС окружностей, если их радиусы равны r и R (задача Эйлера).

Ответ:

 

Используя различные приемы, решите следующие задачи (187—265):

Задание 187.

Периметр прямоугольного треугольника равен 70, а радиус описанной около него окружности равен 14,5. Найдите плошадь треугольника.

Ответ:

210

Задание 188.

В равнобедренном треугольнике боковая сторона равна 20, а диаметр описанной около треугольника окружности равен 25. Найдите радиус вписанной окружности.

Ответ:

6

Задание 189.

Около АВС, где ВС = 12, описана окружность радиусом 10. Найдите длины сторон АБ и АС треугольника, если известно, что радиус ОА окружности делит сторону ВС на два равных отрезка.

Ответ:

Задание 190.

Сторона равностороннего треугольника ABC равна 14. Через его центр проведена прямая I, пересекающая сторону BС и проходящая на расстоянии

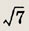
от середины стороны АВ. В каком отношении прямая L делит сторону BС?

Решение.

Пусть D — середина АВ, О — центр АВС,

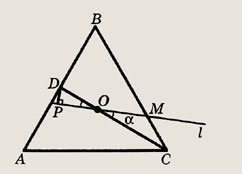
Так как CD — медиана, то

Таким образом,

По теореме синусов

откуда

Ответ:

3 : 2

Задание 191.

В PQR на стороне PQ взята точка N, а на стороне PR — точка L, так что NQ = LR. Точка пересечения
отрезков QL и NR делит отрезок QL в отношении m : n, считая от точки Q. Найдите отношение PN : PR.

Указание.

Примените теорему синусов к NOQ, LOR и РNR (О — точка пересечения QL и NR).

Ответ:

n : m

Задание 192.

В KLM прямая, параллельная стороне LM, пересекает сторону KL в точке А, а сторону КМ — в точке В. Площадь трапеции ALMB в 3 раза меньше площади АВК. Найдите отношение MB : МК.

Ответ:

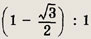
Задание 193.

Через точку О, лежащую внутри АBС, проведены прямые, параллельные сторонам этого треугольника. Площади образовавшихся треугольников равны S₁ , S₂ и S₃. Найдите площадь исходного треугольника.

Решение.

Треугольники ABC, RNO, OPQ и ТОМ

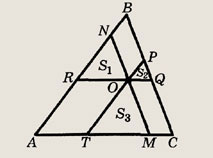
подобны, причем их площади относятся как квадраты коэффициентов подобия. Пусть S — площадь АВС. Тогда

Ответ:

Задание 194.

Через точку О, лежащую внутри АBС, и вершины А и B этого треугольника проведены прямые АО и BО, пересекающие стороны ВС и АС в точках D и Е соответственно. Площади АОЕ, АОБ и BOD равны соответственно S₁ , S₂ и S₃. Найдите площадь четырехугольника EODC.

Решение.

Площади треугольников АОЕ и АОВ, a также DOE и BOD

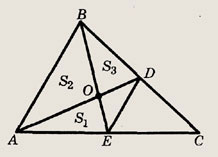
относятся как ОЕ : OB, т.е.

откуда

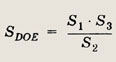
Обозначим площадь EDC через х. Так как

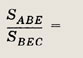
Искомая площадь равна .

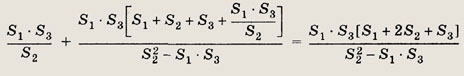
Ответ:

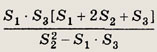
Задание 195.

В равнобедренном остроугольном треугольнике АBС основание АС равно 24, а растояние от вершины B до точки пересечения высот равно 7. Найдите площадь треугольника.

Решение.

Пусть BD и АН — высоты АВС.

Положим

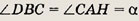
Отрезок

С другой стороны,

Получаем уравнение

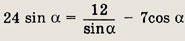
откуда

и

Ответ:

192

Задание 196.

Основание равнобедренного треугольника равно 12, а расстояние от вершины треугольника, лежащей на
основании, до точки пересечения биссектрис равно

Найдите периметр треугольника.

Ответ:

32

Задание 197.

В АBС медианы AM и CN пересекаются в точке О. Известно, что

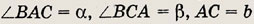
Найдите расстояние от точки О до прямой АС.

Указание.

По теореме синусов найдите АВ. Затем найдите высоту ВН и воспользуйтесь тем, что искомое расстояние равно 1/3 высоты.

Ответ:

Задание 198.

На сторонах острого угла с вершиной О взяты точки А и B. На луче (ОB) взята точка М на расстоянии 3 • ОА от прямой (ОА), а на луче (ОА) — точка N на расстоянии 3 • ОB от прямой (ОB). Радиус окружности, описанной около АОB, равен 3. Найдите длину отрезка MN.

Решение.

Пусть

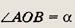
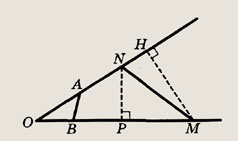
Тогда

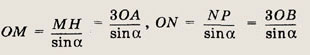
Треугольники АОВ и МОN подобны c коэффициентом подобия

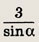
Значит

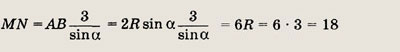
Ответ:

18

Задание 199.

Катеты прямоугольного треугольника равны 9 см и 12 см. Найдите расстояние между точкой пересечения биссектрис и точкой пересечения медиан треугольника.

Ответ:

Задание 200.

Центр окружности, касающийся катетов АС и ВС прямоугольного треугольника ABC, лежит на гипотенузе АВ. Найдите радиус окружности, если он в 6 раз меньше суммы катетов, а площадь АВС равна 27.

Ответ:

3

Задание 201.

В АВС угол В — прямой, АВ = 5, ВС = 4. Точка D лежит на стороне АС, М и N — точки пересечения медиан в ABD и DВС соответственно. Найдите площадь BMN.

Ответ:

Задание 202.

Прямая, проходящая через вершину А равнобедренного треугольника ABC (АВ = ВС) и центр О вписанной в этот треугольник окружности, пересекает сторону ВС в точке К. Известно, что АО : ОК = 1,4. Найдите < ВАС.

Решение.

Проведем КР перпендикулярно АС

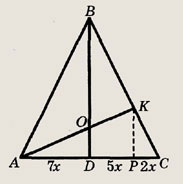
По теореме Фалеса

Положим AD = 7x, DP = 5х, PC = DC - DP = AD - DP = 2x. По той же теореме

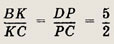
но АК — биссектриса, значит,

Теперь из прямоугольного треугольника ABD находим

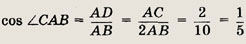
Ответ:

Задание 203.

В АВС проведена средняя линия MN, соединяющая стороны АВ и ВС. Окружность, проведенная через точки М, N и С, касается стороны АВ, а ее радиус равен

Найдите синус < ACB, если длина стороны АС равна 2.

Указание.

Треугольники ANC и CNM подобны, поэтому

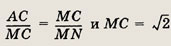
Примените теперь теорему синусов к MNC.

Ответ:

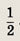
Задание 204.

В равнобедренном треугольнике ABC (АВ = ВС) биссектрисы AM и ВК пересекаются в точке О. Площади ВОМ и СОМ соответственно равны 25 и 30. Найдите площадь АВС и проекцию отрезка ОМ на прямую ВС.

Ответ:

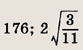
Задание 205.

В АВС на сторонах АВ и АС взяты соответственно точки D и Е так, что CD — биссектриса,

Найдите CD и площадь АВС.

Ответ:

Задание 206.

Около равнобедренного треугольника ABC (АВ = ВС) описана окружность. Биссектриса угла ВАС пересекает окружность в точке D. Касательная к окружности, проходящая через точку D, пересекает прямую АС в точке Е. Найдите длины отрезков CD и DE, если

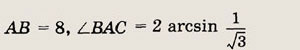
Ответ:

Задание 207.

Около МКН описана окружность с радиусом r и центром в точке О. Длина НМ равна а, а для сторон МКН выполнено соотношение НК² - НМ² = НМ² - МК². Найдите площадь OKL, где L — точка пересечения медиан MКН.

Ответ:

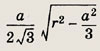
Задание 208.

Касательная, проведенная через вершину М вписанного в окружность KLM, пересекает продолжение стороны KL за вершину L в точке N. Известно, что радиус окружности равен 2,

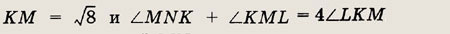
Найдите длину касательной MN.

Ответ:

Задание 209.

Касательная, проведенная через вершину С вписанного в окружность АВС, пересекает продолжение стороны АВ за вершину В в точке D. Известно, что радиус окружности равен

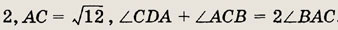
Найдите длину секущей AD.

Решение.

Пусть

— соответственно углы при вершинах А, В и С АBС, угол < CDA.

По теореме синусов

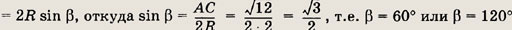
Так как

откуда

Используя условие

получаем

Опустим из точки В перпендикуляр BE на CD. Так как

то четырехугольник ОВЕС — квадрат и BE = ОС = R.

Из прямоугольного треугольника BED следует, что

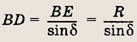
По теореме синусов из АВС получим

Теперь находим

С учетом того, что

имеем

Остается подставить в последнее равенство два возможных значения ß (60° или 120°):

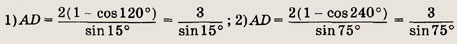
Ответ:

Задание 210.

Внутри АВС выбрана точка О так, что радиусы описанных около АОС и АОB окружностей равны соответственно 5 и 4. Известно, что расстояние между центрами этих окружностей равно 6, АВ = 6, АС = 7. Найдите длину отрезка ОС.

Указание.

Пусть О₁ и О₂ — центры окружностей, описанных около треугольников АОС и АОD соответственно,

По теореме синусов

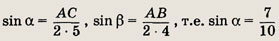
По теореме Герона площадь

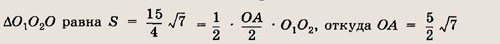
Теперь можно найти ОС по теореме косинусов из АОС.

Ответ:

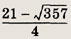
Задание 211.

Внутри АВС выбрана точка О, так, что

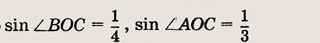
Известно, что ВО = 2, ВС = 3, АС = 4. Найдите расстояние между центрами окружностей, описанных около АОС и ВОС.

Ответ:

Задание 212.

В АВС точка О — центр описанной окружности, точка L лежит на отрезке АВ и AL = LB. Описанная около ALO окружность пересекает прямую АС в точке К. Найдите площадь АВС, если < LOA = 45°, LK = 8, АК = 7.

Решение.

Прямые OL и АВ перпендикулярны (OL — часть диаметра окружности, описанной около АВС, a L — середина АВ;).

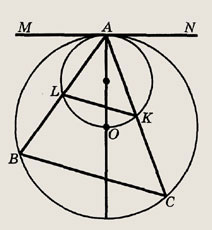
Таким образом, < ALO = 90°. Значит, АО является диаметром окружности, описанной около ALO, откуда следует, что обе окружности касаются друг друга в точке А. Проведем их общую касательную MAN. Углы < NAK и < ALK равны (первый образован касательной AN и хордой АК и опирается на дугу АК; второй - вписан в меньшую окружность и опирается на ту же дугу). Аналогично,

(по двум углам); поскольку радиусы описанных около этих треугольников окружностей относятся как 2:1, так же относятся их стороны, а их площади как 4:1. Найдем площадь S_ALK. Углы < AKL и < AOL равны между собой и равны 45°, так как они вписаны в меньшую окружность и опираются на одну и ту же дугу.
Поэтому

Ответ:

Задание 213.

В АВС через вершины А и B проведена окружность, пересекающая стороны ВС и АС в точках D и Е соответственно. Площадь CDE в 7 раз меньше площади четырехугольника ABDE. Найдите хорду DE и радиус окружности, если АВ = 4 и < C = 45°.

Ответ:

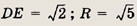
Задание 214.

В

Хорда KN окружности, описанной около АВС, пересекает отрезки АС и BС в точках М и L соответственно. Известно, что < ABC = < CML, площадь четырехугольника AMBL равна 2, LM = 1. Найдите высоту KNC, опущенную из вершины С, и его площадь.

Решение.

Треугольники ABC и CML

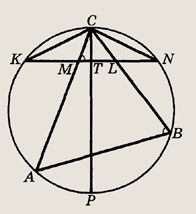
подобны по трем углам, причем коэффициент подобия равен

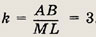
Следовательно, отношение площадей АВС и MCL равно 9. Зная площадь четырехугольника AMLB и обозначив площадь AMCL через S, получим уравнение

Далее, по известному углу АСВ и хорде АВ вычислим радиус описанной около АВС окружности:

Угол CMN измеряется полусуммой дуг

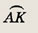
и

(он равен сумме двух углов < KNA и < CAN как внешний угол AMN, а эти углы — вписанные в окружность и опираются на дуги

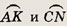
Но < CMN = < CBA по условию и угол СВА опирается на дугу

а это влечет равенство хорд

Следовательно, KCN — равнобедренный. Тогда высота СТ KCN является, во-первых, медианой (откуда КТ = TN) и, во-вторых, — частью диаметра СР. Согласно свойству пересекающихся хорд имеем КТ • TN = СТ • ТР.

Высоту СТ можно найти из соотношения

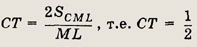
Тогда

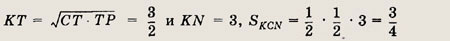
Ответ:

Задание 215.

В

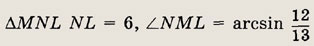
Хорда AD окружности, описанной около MLN, пересекает отрезки MN и ML в точках В и С соответственно. Известно, что < NLM = < MBC, площадь четырехугольника NLCB равна 9, ВС = 3. Найдите высоту AMD, опущенную из вершины М, и его площадь.

Ответ:

2; 6

Задание 216.

Окружность, вписанная в равнобедренный треугольник ABC, касается основания АС в точке D и боковой стороны АВ в точке Е. Точка F — середина стороны АВ, a G -- точка пересечения окружности и отрезка FD, отличная от D. Касательная к окружности, проходящая через точку G, пересекает сторону АВ в точке Н. Найдите < BCA, если известно, что FH : НЕ = 2 : 3.

Указание.

Пусть

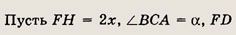
— средняя линия АВС. Возможны два случая расположения точки Н: на отрезке BE и на отрезке АЕ. Из теоремы синусов для FGH запишите уравнение

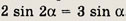
Ответ:

Задание 217.

На отрезке АВ взята точка С, отрезки АВ и СВ служат диаметрами окружностей. Хорда AM касается меньшей окружности в точке D. Прямая BD пересекает большую окружность в точке

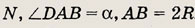
Найдите площадь четырехугольника ABMN.

Указание.

Площадь четырехугольника равна половине произведения диагоналей на синус угла между ними. Угол между диагоналями AM и BN выразите через а, заметив, что OD II ВМ, где OD — радиус окружности с диаметром СВ.

Ответ:

Задание 218.

Две окружности пересекаются в точках А и В. Хорда CD первой окружности имеет с хордой EF второй окружности общую точку М. Отрезок АВ втрое больше отрезка СМ, который, в свою очередь, вдвое меньше отрезка MD и в 6 раз меньше отрезка MF. Найдите длину отрезка AM, если ЕМ = 2, АВ = 9МЕ.

Решение.

Пусть ME = х

Тогда АВ = 9x, СМ = = 3x, MD = 6x, FM = 18х. Заметим, что FM • ME = 18x² = СМ • MD. Покажем, что точки F, С, Е, D лежат на одной окружности. Действительно, проведем окружность и через точки F, С, Е. Она пересекает прямую CD в точке D'. Согласно свойству пересекающихся хорд должно выполняться соотношение FM • ME = СМ • MD'. Но тогда MD = MD', а это означает, что точка D — D' лежит на проведенной окружности.

Окружность

пересекает данные в условии окружности

поочередно в точках

Следовательно, окружности

будут пересекаться как показано на рис., где следует учесть тот факт, что точки С к D можно поменять местами и то же самое можно сделать с точками E и F (это будет учтено ниже).

Покажем теперь, что хорда АВ пересекает хорды CD и EF в их общей точке пересечения М. Проведем через А и М прямую.

Отсюда следует, что МК = ML, а это возможно лишь если К = L = В, т.е. хорда АВ проходит через точку М. Значит, хорды АВ и CD пересекаются в точке М и, кроме того, они равны, поскольку CD = СМ + MD = 9х = АВ.

Ответ:

1 или 4

Задание 219.

Каждая из трех равных окружностей радиуса r касается двух других. Найдите площадь треугольника, образованного общими внешними касательными к этим окружностям.

Ответ:

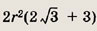
Задание 220.

Две окружности касаются друг друга внешним образом в точке А. Через точку В на их общей касательной АВ проведены две прямые, одна из которых пересекает первую окружность в точках N и М, а другая — вторую окружность в точках Р и Q. Известно что АВ = 6; ВМ = 9, ВР = 5. Найдите отношение площадей MCW и QOP, где О — точка пересечения прямых МР и NQ.

Указание.

Используя равенство АВ² = ВМ • BN = BQ • ВР

найдите отрезки PQ, BN и MN. Докажите подобие треугольников BQN и РМВ. Отсюда будет вытекать равенство углов QPO и ONM и, как следствие, подобие треугольников QOP и MON.

Ответ:

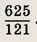
Задание 221.

В некоторый угол В вписаны две непересекающиеся окружности. Окружность большего радиуса касается сторон этого угла в точках А и С, меньшего — в точках А₁ и С₁ (точки А, А₁ и С, G₁ лежат на разных сторонах угла B). Прямая АС₁ пересекает окружности большего и меньшего радиусов в точках Е и F соответственно. Найдите отношение площадей АВС₁ и А₁ВС₁, если А₁В = 2, EF = 1, а длина АЕ равна среднему арифметическому длин BC₁ и EF.

Ответ:

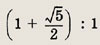
Задание 222.

Диаметр АВ и хорда CD окружности пересекаются в точке Е, причем СЕ = ED. Касательные к окружности в точках B и С пересекаются в точке К, а отрезки АК и СЕ — в точке М. Найдите площадь CKM, если АВ = 10, АЕ = 1.

Решение.

Согласно свойству пересекающихся хорд СЕ • ED = = АЕ • ЕВ

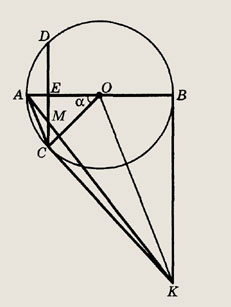
откуда СЕ = 3. Пусть О — центр окружности, а

Прямоугольные треугольники СОК и ВОК равны. Поэтому

Треугольники AЕС и ОВК подобны, откуда

Так как

и треугольники АЕМ и АВК подобны, откуда

Ответ:

Задание 223.

Точка М делит диагональ АС квадрата ABCD со стороной а в отношении AM : МС = 3 : 1 Точка N лежит на АВ, причем < NMD = 90°. Найдите длину AN.

Решение.

Проведем PQ перпендикулярно АВ

Треугольники АРМ и ABC подобны с коэффициентом подобия

т.е.

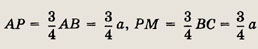
Аналогично, из подобия треугольников MQC и ADC получаем

Прямоугольные треугольники NPM и MQD равны по катету и острому углу <QDM = < PNM как углы со взаимно перпендикулярными сторонами). Отсюда следует, что

Ответ:

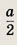
Задание 224.

Сторона квадрата ABCD равна 4. Через вершину D проведена прямая L, пересекающая сторону ВС и проходящая на расстоянии 2 от середины стороны АВ. В каком отношении прямая L делит сторону ВС?

Ответ:

1 : 3

Задание 225.

Основания трапеции равны а и b. Прямая пересекает боковые стороны трапеции так, что одну из них делит пополам, а другую в отношении 1 : 3. Определите, в каком отношении прямая делит площадь трапеции.

Ответ:

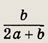
Задание 226.

Длина средней линии трапеции равна 5. Средняя линия делит трапецию на части, отношение площадей которых равно

Найдите высоту трапеции, если известно, что в нее можно вписать окружность.

Ответ:

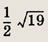
Задание 227.

Найдите длину стороны квадрата, две вершины которого лежат на окружности радиуса

а две другие — на касательной к этой окружности.

Ответ:

Задание 228.

Из вершины острого угла ромба проведены перпендикуляры к прямым, содержащим стороны ромба, которым не принадлежит эта вершина. Длина каждого перпендикуляра равна 3, а расстояние между их основаниями

Вычислите длины диагоналей ромба.

Ответ:

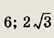
Задание 229.

Около окружности описаны ромб со стороной 3 и треугольник, две стороны которого параллельны диагоналям ромба, а третья параллельна одной из сторон ромба и равна 7. Найдите радиус окружности.

Решение.

Пусть ABCD — ромб и NPM — прямоугольный треугольник, описанный около данной окружности

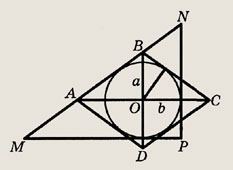
Поскольку АВ и MN — параллельные касательные к одной окружности, они лежат на одной прямой. Через а и b обозначим половины диагоналей ромба. Треугольники ВОС и NPM подобны с коэффициентом подобия

т.е. стороны прямоугольного треугольника NPM равны

Искомый радиус является высотой в прямоугольном треугольнике ВОС и равен

Кроме того, r — радиус вписанной в NMP окружности, т.е.

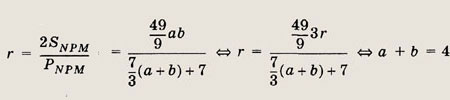
В прямоугольном треугольнике ВОС имеем а² + b² = 9. Решаем систему

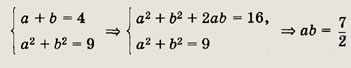
откуда

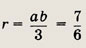
Ответ:

Задание 230.

Основание AD трапеции ABCD является диаметром окружности радиуса 2. Прямая, содержащая среднюю линию трапеции, пересекает окружность в точках М и N. Известно, что АВ = ВС = CD = 2. Найдите длину отрезка MN.

Ответ:

Задание 231.

В равнобочную трапецию с периметром 100 см вписана окружность. Найдите радиус окружности, если расстояние между точками касания окружности и боковых сторон равно 16 см.

Решение.

Пусть М, L, N, К — точки касания вписанной окружности со сторонами АВ, ВС, CD, DA соответственно; r — ее радиус, а О — центр; Е — точка пересечения отрезков MN и KL; BF — высота трапеции

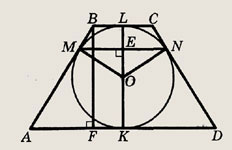
Положим АК = х, BL = у, ME = а. Отрезки касательных, проведенных к окружности из одной точки, равны, поэтому AM = АК = х, ВМ = BL = у. Так как К и L — середины оснований трапеции, то

АК+АВ + ВЬ=АК + AM + MB + BL = 2(х + у) = 50.

Поскольку в прямоугольных треугольниках BFA и MEO < BAF и < МОЕ равны как углы с соответственно перпендикулярными сторонами, эти треугольники подобны. Значит,

а так как по условию

С учетом равенства (*) получаем

Ответ:

10 см.

Задание 232.

Трапеция ABCD с основаниями ВС = 2 см и AD = 10 см такова, что в нее можно вписать и около нее можно описать окружность. Найдите отношение радиусов описанной и вписанной окружностей. Определите, находится ли центр описанной окружности внутри трапеции или вне ее.

Решение.

Так как около трапеции можно описать окружность, то она равнобочная (АВ = CD). Далее, так как в нее можно вписать окружность, то АВ + CD = ВС + AD =12 см, откуда АВ = CD — 6 см.

Пусть СН — высота трапеции

Имеем

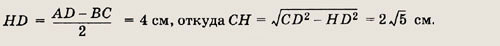
Значит, радиус вписанной окружности

Полагая

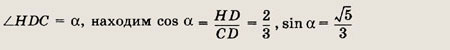
Применив теорему косинусов к ACD, получим

Окружность, описанная около трапеции ABCD, описана и около ACD, откуда

Чтобы ответить на второй вопрос задачи, достаточно определить тип АСD. Так как

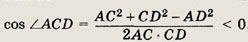
то треугольник тупоугольный и центр описанной окружности лежит вне треугольника, ниже стороны AD, а следовательно, вне трапеции ABCD.

Ответ:

вне трапеции.

Задание 233.

Центр окружности, вписанной в прямоугольную трапецию удален от концов боковой стороны на расстояния 8 см и 4 см. Найдите среднюю линию трапеции.

Решение.

Пусть О — центр вписанной окружности, АВ — боковая сторона, перпендикулярная основанию, ОС = 4 см, OD = 8 см

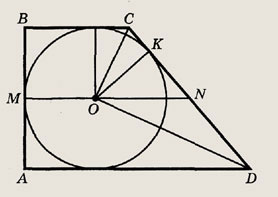
Углы OCD и ODC — половины углов BCD и CDA, которые в сумме составляют 180°. Следовательно, < OCD + < ODC = 90° и ОСD — прямоугольный.

Таким образом,

Ответ:

Задание 234.

Около трапеции с основаниями AD и ВС описана окружность радиуса 6 см. Центр описанной окружности лежит на AD, ВС = 4. Найдите площадь трапеции.

Ответ:

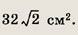
Задание 235.

Трапеция KLMN с основаниями LM и KN вписана в окружность, центр которой лежит на KN. Диагональ LN равна 4 см, < MNK = 60°. Найдите длину основания LM.

Ответ:

Задание 236.

В трапеции углы при одном из оснований равны 20° и 70°, а длина отрезка, соединяющего середины оснований, равна 2 см. Найдите меньшее основание трапеции, если длина ее средней линии 4 см.

Ответ:

2 см.

Задание 237.

В трапеции ABCD основание ВС = 1 см, основание AD = 2 см. Проведена прямая, параллельная основаниям и пересекающая боковые стороны АВ и CD в точках Р и Q соответственно, а диагонали АС и BD — в точках L и R. Отрезки АС и BD пересекаются в точке О. Найдите PQ, если площадь ВОС равна площади LOE.

Решение.

Треугольники ВОС и LOR подобны

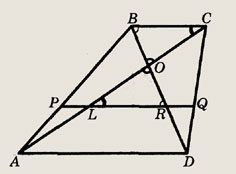
Поскольку отношение площадей подобных треугольников равно квадрату коэффициента подобия, эти треугольники равны. Отсюда следует, что LR = ВС = 1 см, ВО = OR и СО = ОL. В AOD отрезок LR равен половине основания AD и параллелен ему, т.е. LR — средняя линия АОD и LR = 1 см.

Значит

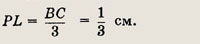
Аналогично,

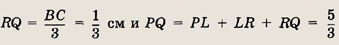
Ответ:

Задание 238.

В трапеции ABCD параллельно основаниям ВС = 1 см и AD = 2 см проведена прямая; пересекающая АВ в точке Р, АС — в точке L, BD — в точке R и CD — в точке Q. Найдите PQ, если LR = PL.

Ответ:

Задание 239.

В трапеции ABCD точка Е лежит на боковой стороне CD. Отрезки BD и АЕ пересекаются в точке О. Найдите площадь DOE, если известно, что DE : ЕС = 2:1, АО : ОЕ — 2 : 1 и площадь АОВ равна 1.

Решение.

Продолжим АЕ до пересечения с продолжением ВС в точке K

Треугольник КЕС подобен треугольнику AED, причем коэффициент подобия равен

Так как

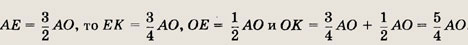
Отношение площадей

Треугольники подобны, причем коэффициент подобия равен

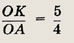
и, следовательно,

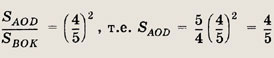
Ответ:

Задание 240.

В трапеции ABCD точка М лежит на боковой стороне АВ. Отрезки BD и СМ пересекаются в точке О. Известно, что AM = ВМ, СО = 4 • ОМ, а площадь ВОМ равна 1. Найдите площадь СOD.

Ответ:

6

Задание 241.

В трапеции ABCD основание AD = 12 см, основание ВС = 3 см. На продолжении ВС взята точка М так, что прямая AM отсекает от трапеции треугольник, площадь которого равна

площади трапеции. Найдите СМ.

Ответ:

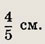
Задание 242.

В трапеции ABCD известны основания:

и углы: < BAD = 30° и < ADC = 60°. Через точку D проходит прямая, делящая трапецию на две равновеликие фигуры. Найдите длину отрезка этой прямой, находящегося внутри трапеции.

Решение.

Сначала найдем стороны трапеции. Пусть ВР и CQ — высоты трапеции

Положим ВР = CQ = h. Треугольники АРВ и CQD —- прямоугольные с острым углом 30° В них отношение большего катета к меньшему равно

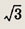
откуда

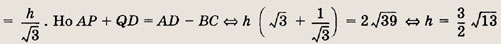
Сторона

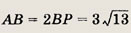
Пусть DK — искомый отрезок. Отношение площадей

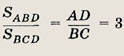
Применив теорему косинусов, получим

KD² = АK² + АD² - 2АК • AD cos 30° = 169, т.е. KD = 13.

Ответ:

13 см.

Задание 243.

В трапеции ABCD AD и ВС -- основания, AD = 30 см, АВ = 3 см, ВС = 12 см, < BAD = 60°. Диагонали трапеции пересекаются в точке Е. Найдите площадь CED.

Ответ:

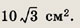
Задание 244.

В трапеции ABCD основание

диагонали АС и BD пересекаются в точке К, причем АК = 1 см, KD = 2 см, < ВАС = < DAC. Найдите площадь трапеции ABCD.

Решение.

Углы АСВ и CAD равны как внутренние накрест лежащие

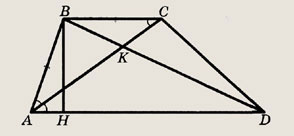
значит, АВС — равнобедренный. По теореме косинусов из АKD находим

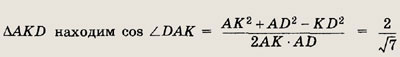
Треугольники подобны, откуда

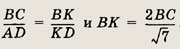
Так как АВ = ВС, то, применив теорему косинусов к АВK, получим

Первый корень лишний: действительно, если

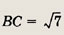
то АВ = ВС = AD, четырехугольник ABCD — ромб и тогда угол < AKD — прямой, что невозможно, поскольку

Таким образом,

Высоты трапеции

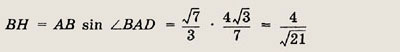
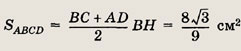
Ответ:

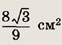
Задание 245.

В прямоугольной трапеции ABCD АВ -- основание,

AD = 4 см. Найдите площадь трапеции ABCD.

Ответ:

Задание 246.

На сторонах АВ, ВС и АD параллелограмма ABCD взяты точки К, М и L так, что АК : KB = 2 : 1, ВМ : МС = 1 : 1, AL : LD = 1 :3. Найдите отношение площадей KBL и BML.

Ответ:

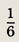
Задание 247.

Внутри параллелограмма ABCD взята точка К, равноудаленная от сторон AD,AB и CD. Перпендикуляр, опущенный из вершины D на АВ, пересекает отрезок АК в точке М. Найдите площадь параллелограмма ABCD, если известно, что DK = 2 см, AM : МК = 8 : 1, a DC = ЗBС.

Решение.

Пусть DP — высота параллелограмма

Так как АК и DK — биссектрисы углов BAD и ADC соответственно, то

т.е. треугольники AKD иМКО — прямоугольные. Пусть МК = х. Тогда

Треугольники подобны с коэффициентом подобия

Точка K равноудалена от сторон АВ, AD и CD, поэтому

Таким образом,

Треугольники АРМ и MKD подобны как прямоугольные с равными острыми углами . Коэффициент подобия равен

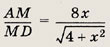
Следовательно,

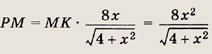
Отсюда

Ответ:

72 см²

Задание 248.

Две параллельные прямые l₁ и l₂ пересекаются с третьей прямой l₃ в точках М и К соответственно. Точка С равноудалена от прямых l₁, l₂ и l₃. Перпендикуляр, опущенный из М на l₂, делит отрезок КС в отношении 15:1, считая от вершины К, СМ = 4 см. Найдите расстояние между прямыми l₁ и l₂.

Ответ:

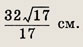
Задание 249.

Окружность с центром в точке О касается сторон АВ, ВС и CD параллелограмма ABCD. Перпендикуляр, опущенный из вершины С на АВ, делит ВО на отрезки 5 см и 4 см, считая от вершины B. Найдите площадь параллелограмма ABCD, если АB = 2BС.

Ответ:

216 см²

Задание 250.

Окружность, проходящая через вершину D и касающаяся сторон АВ и ВС равнобочной трапеции ABCD, пересекает стороны AD и DC в точках М и N так, что AM : MD = 1 : 3, CN : ND = 4 : 3. Найдите длину стороны ВС, если АВ = 7 см, AD = 6 см.

Ответ:

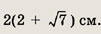
Задание 251.

Стороны KN и LM трапеции KLMN параллельны, причем KN = 3 см, < LMN = 120°. Прямые LM и MN являются касательными к окружности, описанной около KLN. Найдите площадь KLN.

Ответ:

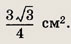
Задание 252.

В трапеции ABCD с основаниями AD и ВС диагонали АС и BD пересекаются в точке Е. Около ВЕС описана окружность. Касательная к этой окружности, проведенная в точке Е, пересекает прямую AD в точке F так, что D лежит между А и F. Найдите EF, если AF = а; AD = b (а > b).

Ответ:

Задание 253.

В выпуклом четырехугольнике ABCD длина отрезка, соединяющего середины сторон АВ и CD, равна 1. Прямые ВС и AD перпендикулярны. Найдите длину отрезка, соединяющего середины диагоналей АС и BD.

Решение.

Пусть М и N — середины CD и АВ соответственно; Р и Q — середины BD u АС

Отрезки MQ и PN — средние линии треугольников ACD и ABD, поэтому MQ и PN параллельны и равный, следовательно, четырехугольникPMQN — параллелограмм. Стороны параллелограмма РМ и MQ параллельны соответственно ВС и AD, т.е. PMQN — прямоугольник. Диагонали прямоугольника равны, поэтому PQ = MN = 1 м.

Ответ:

1 м.

Задание 254.

В выпуклом четырехугольнике ABCD диагонали АС и BD перпендикулярны. Длина отрезка, соединяющего середины сторон АВ и CD, равна 1 м. Найдите длину отрезка, соединяющего середины сторон ВС и AD.

Ответ:

1 м.

Задание 255.

В выпуклом четырехугольнике ABCD длина стороны AD равна 4, длина стороны CD равна 7,

Найдите сторону ВС, если известно, что окружность, описанная около АВС, проходит также и через точку D.

Ответ:

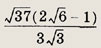
Задание 256.

В выпуклом пятиугольнике ABCDE диагонали BE и СЕ являются биссектрисами углов при вершинах В и С соответственно, < A = 35°, < D = 145°, а площадь ВСЕ равна 11. Найдите площадь пятиугольника ABCDE.

Указание.

Пусть А' — точка, симметричная точке А относительно серединного перпендикуляра к отрезку BE, a D' — точка, симметричная точке D относительно серединного перпендикуляра к отрезку СЕ. Четырехугольник A'BCD' — параллелограмм, точка ? лежит на A'D', а площадь его равна площади ABCDE.

Ответ:

22

Задание 257.

Диагонали вписанного в окружность четырехугольника ABCD пересекаются в точке Е, причем

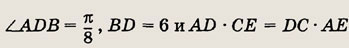
Найдите площадь четырехугольника ABCD.

Указание.

Так как

поэтому Е — точка пересечения биссектрисы угла ADC со стороной AC ACD. Следовательно,

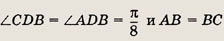
На луче DC отложите отрезок СМ = AD. Треугольник ВСМ равен треугольнику ABD. Поэтому искомая площадь равна площади равнобедренного треугольника DBM.

Ответ:

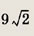
Задание 258.

Окружность касается сторон AD, BC и AS трапеции ABCD. Через точку М, лежащую на основании AD и отстоящую от D на 10 см, проведена касательная к окружности, пересекающей основание ВС трапеции в точке К. Найдите отношение площадей четырехугольников АВКМ и MDCK, если AD = 40 см, АВ = CD = 10 см, <BAD = 60°.

Ответ:

Задание 259.

Окружность касается прямых АВ и ВС в точках D и Е соответственно. Точка А лежит между точками D и В, а точка С — между В и Е. Найдите площадь АВС, если известно, что АВ = 13 см, АС = 1 см, а точки A, D, E и С лежат на одной окружности.

Ответ:

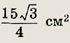
Задание 260.

Окружность касается сторон АВ и ВС АВС соответственно в точках D и Е. Найдите длину высоты, опущенной из точки А, если АВ = 5 см, АС = 2 см, а точки А, D, E и С лежат на одной окружности.

Ответ:

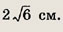
Задание 261.

Из точки С проведены две прямые, касающиеся заданной окружности в точках А и В. На большей из дуг АВ взята точка D так, что

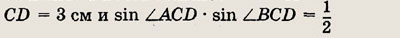
Найдите расстояние от точки D до прямой АВ.

Ответ:

Задание 262.

Окружность касается сторон угла в точках А и В, O — вершина угла. На этой окружности внутри АОВ взята точка С. Расстояние от точки С до прямых ОА и ОB равно а и b соответственно. Найдите расстояние от точки С до прямой АВ.

Ответ:

Задание 263.

На плоскости дан прямой угол. Окружность с центром внутри этого угла касается одной стороны угла, пересекает другую сторону в точках А и В, а биссектрису угла — в точках С и D. Найдите радиус окружности, если

Решение.

Опустим из точки О перпендикуляры ОМ, ON и OL на стороны угла и на биссектрису

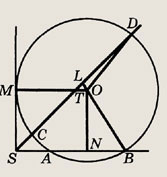
Обозначим радиус окружности через R. В прямоугольном треугольнике ONB имеем

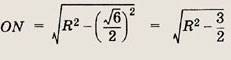
Анадогично из прямоугольного треугольника OLD следует, что

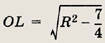
Пусть Т — точка Пересечения ОМ и DC, a S — вершина прямого угла. Треугольник MST — прямоугольный и равнобедренный, поэтому

Треугольник TLO — также прямоугольный и равнобедренный, и, значит,

поэтому для нахождения R получаем уравнение

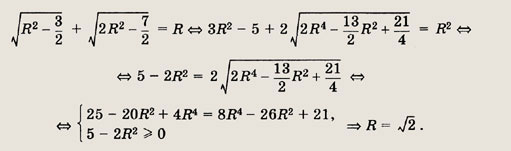
Ответ:

Задание 264.

На плоскости дан прямой угол. Окружность с центром вне этого угла пересекает одну из сторон в точках
А и В, а продолжение другой стороны — в точках С и D. Найдите радиус окружности, если

Ответ:

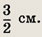
Задание 265.

На плоскости дан угол величиной

Окружность касается одной стороны угла, пересекает другую в точках А и B, а биссектрису угла — в точках С и D. Найдите площадь круга, если

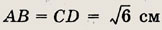
Ответ:

3П см²

 

В следующих задачах требуется установить, какое наибольшее или наименьшее значение может принимать та или иная геометрическая величина (266—282):

Задание 266.

Равнобедренный треугольник вписан в окружность радиуса R. Найдите наибольшее значение длины высоты, опущенной на боковую сторону.

Решение.

Пусть а — угол при вершине В в АВС

тогда

Проведем высоту АН. Так как угол

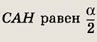
то

Поэтому задача сводится к отысканию максимального значения функции

на отрезке [0; П]. Найдем производную функции F:

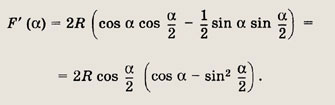
Определим нули производной:

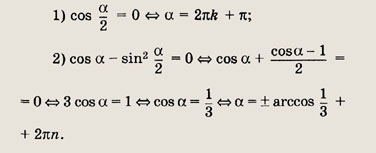
Из этих решений на интервале (0; П) лежит лишь один корень

Вычислим значения функции

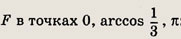
Следовательно, наибольшая длина высоты равна

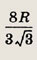
Ответ:

Задание 267.

Высота прямоугольного треугольника, опущенная на гипотенузу, равна h. Найдите наименьшее значение длины медианы треугольника, проведенной к большему катету.

Ответ:

Задание 268.

В

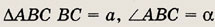
Найдите наибольшее значение периметра треугольника.

Решение.

Пусть < ABC = х,АВ = с,АС = b

тогда

Задача сводится к нахождению максимального значения функции Р(х)

Производная

равна нулю, если

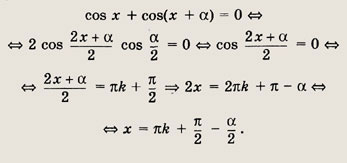
На интервале

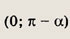
лежит только корень

Вычислим значения функции Р(х) в точках

Таким образом, максимальное значение функции р(х) равно

Ответ:

Задание 269.

Середины высот АВС лежат на одной прямой. Наибольшая сторона треугольника АВ = 10. Какое максимальное значение может принимать площадь треугольника?

Ответ:

25

Задание 270.

Боковые стороны и меньшее основание трапеции равны по 10 см. Каким должно быть ее большее основание, чтобы площадь трапеции была наибольшей?

Ответ:

20 см.

Задание 271.

При каком значении длины высоты прямоугольная трапеция с острым углом 45° и периметром 8 см имеет наибольшую площадь?

Ответ:

Задание 272.

Найдите наименьшее возможное значение периметра параллелограмма с острым углом 30° и площадью 4 см².

Ответ:

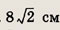
Задание 273.

Диагонали выпуклого четырехугольника пересекаются под прямым углом, сумма их длин равна 8 см.
Каково наибольшее возможное значение площади четырехугольника?

Ответ:

8 см²

Задание 274.

Две вершины прямоугольника лежат на диаметре полуокружности, а две другие — на самой полуокружности радиуса 2 м. Найдите наибольшее значение площади прямоугольника.

Ответ:

4 м²

Задание 275.

Площадь трапеции, описанной около окружности, равна 8 см². Найдите радиус окружности, если известно, что сумма длин боковых сторон и высоты трапеции принимает минимально возможное значение.

Решение.

Согласно свойству четырехугольника, описанного около окружности, АВ + CD = ВС + AD

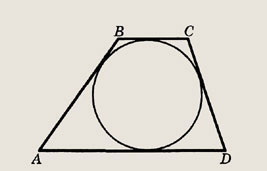
Пусть 2х — высота трапеции. Тогда радиус вписанного круга равен х. Площадь трапеции равна

Сумма боковых сторон и высоты равна сумме оснований и высоты, т.е.

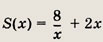
В задаче требуется найти значение х, при котором функция

принимает наименьшее значение.

Так как

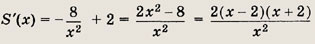
то производная обращается в нуль при х = 2, причем меняет в этой точке знак с минуса на плюс, т.е. х₀ = 2 — минимум.

Ответ:

2 см.

Задание 276.

В равнобедренный треугольник с длинами сторон 15, 15 и 18 см вписан параллелограмм наибольшей площади так, что угол при основании у них общий. Найдите периметр параллелограмма.

Ответ:

33 см.

Задание 277.

В трапеции ABCD основания AD = 10 см, ВС = 6 см, боковая сторона АВ = 8 см и перпендикулярна основаниям. Внутри трапеции расположен прямоугольник, у которого одна из сторон лежит на большем основании трапеции. Найдите наибольшее значение площади прямоугольника.

Ответ:

48 см²

Задание 278.

Периметр кругового сектора равен L. Найдите величину центрального угла сектора, при котором его площадь является наибольшей.

Решение.

Пусть радиус сектора равен R, а угол АОВ равен а

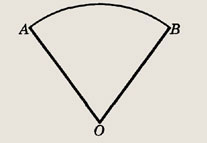
тогда периметр сектора

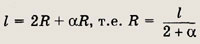
Площадь сектора

Будем искать максимальное значение S(a) при a € [0; 2П]. Найдем производную

Следовательно,

Ответ:

2 рад.

Задание 279.

Из имеющихся досок можно построить забор длиной 200 м. Определите максимальную площадь двора прямоугольной формы, который можно огородить этими досками, если для одной стороны двора можно использовать стену близлежащего здания.

Ответ:

5000 м²

Задание 280.

На окружности радиуса r дана точка А. На каком расстоянии от точки А нужно провести хорду ВС, параллельную касательной к окружности в точке А, чтобы площадь АВС была наибольшей?

Ответ:

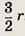
Задание 281.

Боковые стороны трапеции перпендикулярны. Какое наибольшее значение может принимать площадь треугольника, образованного диагоналями и средней линией трапеции, если известно, что длины оснований трапеции равны а и b?

Ответ:

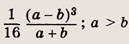
Задание 282.

На координатной плоскости рассматриваются всевозможные треугольники ABC, у каждого из которых < АСВ = 90°, вершина А имеет координаты (1; 0), вершина С лежит на отрезке [0; 1] оси Ох, а вершина В — на параболе у = х - х². Какие координаты должна иметь вершина В, чтобы площадь ASC была наибольшей?

Решение.

Пусть точка С имеет координаты (t; 0); тогда (t; t - t²) — координаты точки В

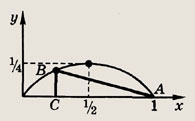
Длина ВС равна t - t², длина АС равна 1 - t. Площадь

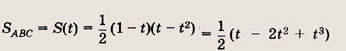
Производная

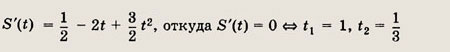
Далее имеем

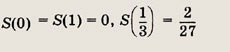
Таким образом, максимальное значение функции достигается при

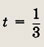
Ответ: