Метод математической индукции. Бином Ньютона.
Элементы комбинаторики. Комплексные числа

1. Метод математической индукции. Пусть для объектов А₁, А₂, ..., А_n, ... требуется установить справедливость некоторого утверждения. Доказательство справедливости методом математической индукции состоит в следующем:

а) проверяем справедливость утверждения для объекта А₁;

б) предполагая справедливость утверждения для A_k, где k — произвольное натуральное число, устанавливаем справедливость его для A_{k + 1}.

Если оба условия оказываются выполненными, то утверждение считается доказанным для всех объектов А_n, n € N (принцип математической индукции).

Метод математической индукции широко применяется при доказательстве теорем, доказательстве справедливости тождеств или неравенств выражений, зависящих от натуральной переменной п, решении задач на делимость и т. д.

Применяя метод математической индукции, докажите, что при любом n € N справедливы следующие утверждения (1-26):

Задание 1.

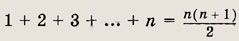
Решение:

Для n = 1 получаем

— верное равенство.

Пусть данное наше утверждение выполняется для

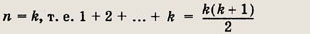
Докажем справедливость исследуемого равенства л
для n = k + 1. Имеем

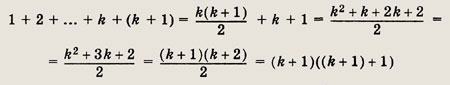
что и требовалось доказать.

Таким образом, исходное равенство выполняется для всех натуральных n.

Задание 2.

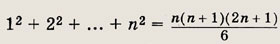
Задание 3.

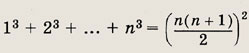
Задание 4.

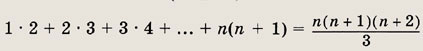
Задание 5.

1 • 4 + 2 • 7 + 3 • 10 + ... + n(3n + 1) = n(n + 1)²

Решение:

Проверяем справедливость данного равенства при n = 1, имеем 1 • 4 = 1(1 + 1)² — верное равенство.
Пусть данное равенство справедливо для n = k, т. е.

1 • 4 + 2 • 7 + ... + k(3k + 1) = k(k + 1)2. Положим n = k + 1. Тогда

1 • -4 + 2 • 7 + ... + k(3k + 1) + (k + 1)(3k +4) = k(k + 1)² +(k + 1)(3k + 4) = k³ + 2k² + k + 3k² + 7k + 4 = k³ + 5k² + 8k + 4.

Разложим последнее выражение на множители. Число k = -1 является корнем этого многочлена. Разделим полученное выражение на k + 1:

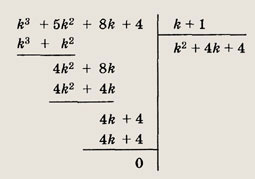
Таким образом,

1 • 4 + 2 • 7 + ... + (k + 1)(3(k + 1) + 1) = (k + 1)((k + 1) + 1)², что и требовалось доказать.

Задание 6.

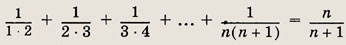
Указание:

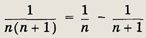
Задание 7.

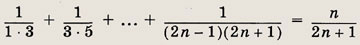
Указание:

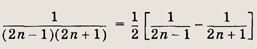
Задание 8.

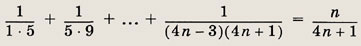
Задание 9.

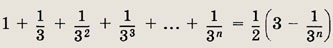
Задание 10.

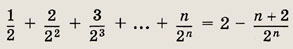
Задание 11.

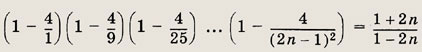
Указание:

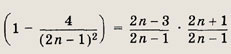
Задание 12.

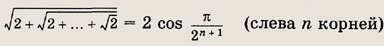
Указание:

Возведите равенство в квадрат и к правой части примените формулу

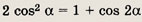
Ответ:

Задание 13.

Указание:

Воспользуйтесь формулой

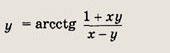
Задание 14.

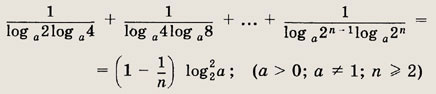
Задание 15.

аⁿ - bⁿ = (а - b) (а^{n - 1} + a^{n - 2}b + a^{n - 3}b² + ... + b^{n - 1}), где a, b € R

Решение:

Преобразуем правую часть доказываемого равенства:

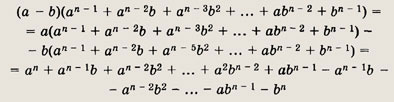
В последнем выражении все слагаемые, кроме первого в первой строке и последнего во второй строке, сократятся. В результате получится аⁿ - bⁿ.

Задание 16.

a²ⁿ + 1 + b²ⁿ + 1 = (a + b) (a²ⁿ - a^2n-1 b + ... - ab^2n-1 + b²ⁿ), где a, b € R. Напомним определение:

0! = 1, n!= 1 • 2 • 3 • ... • n (читается: «эн факториал»).

 

Решите задачи 17—20, используя это определение.

Задание 17.

1 • 1! + 2 • 2! + ... + n • n! = (n + 1)! - 1

Решение:

Для n = 1 равенство имеет вид 1 • 1! = (2)! - 1 — тождество. Пусть равенство справедливо для n = k. Положим n = k + 1; тогда, используя предположение индукции, получим

1 • 1! + 2 • 2! + ... + k • k! + (k + 1)(k + 1)! = (k + 1)! - 1 + (k + 1)(k + 1)! = (k + 1)!(1 + (k + 1)) - 1 = (k + 1)!(k + 2) - 1 = (k + 2)! - 1,

что и требовалось доказать.

Задание 18.

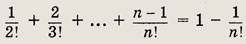
Задание 19.

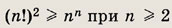
Решение:

Для n = 1 неравенство имеет вид

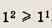
т. е. оно выполнено. Пусть данное неравенство имеет место для n = k. Докажем его справедливость для n = k + 1. Для этого достаточно доказать, что

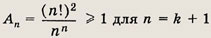
при этом согласно предположению индукции

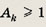
Рассмотрим отношение

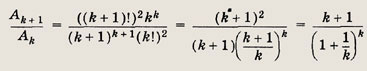
Раскрывая знаменатель последнего выражения, получаем

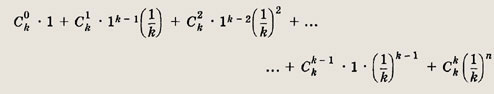
Количество слагаемых равно (n + 1). Слагаемые имеют вид

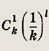
где l = 0, 1, ..., k, при этом

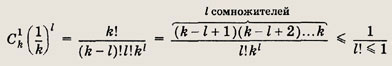
Отсюда следует, что знаменатель выражения меньше или равен n + 1 и отношение

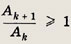
Так как по предположению индукции

неравенство доказано.

Задание 20.

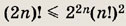
Задание 21.

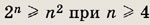
Задание 22.

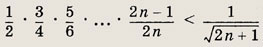
Задание 23.

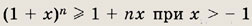
Задание 24.

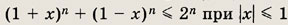
Указание:

Воспользуйтесь неравенством (предварительно доказав его!)

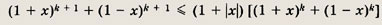
Задание 25.

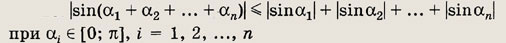
Указание:

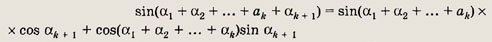
Задание 26.

Пустьx₁, ..., х_n — произвольные положительные числа, удовлетворяющие равенству х₁ • х₂ • ... • х_n = 1. Докажите, что

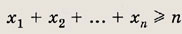
Решение:

Для n = 1 неравенство очевидно. Пусть оно выполняется для n = k. Докажем его справедливость для n = k + 1.

Так как x₁ • x₂ • ... • x_k • x_k+1 = 1, то, переставив сомножители, можно добиться, чтобы

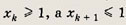
Применив предположение индукции для произведения k чисел получаем

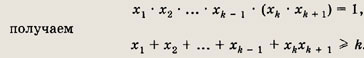
Учитывая, что

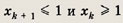
имеем

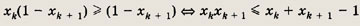
Теперь если в левую часть неравенства вместо x_k x_k+1 подставить выражение x_k + x_k+1 - 1, то неравенство сохранится, т. е.

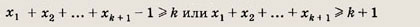
что и требовалось доказать.

Используя результат задачи 26, докажите следующее неравенство между средним арифметическим и средним геометрическим произвольных положительных чисел:

Задание 27.

Если a_i > 0, i = 1, 2,..., n, то

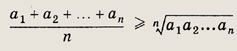
В каком случае это неравенство обращается в равенство?

Указание:

Положите

 

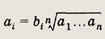
В задачах 28, 29 используйте результат задачи 27.

Задание 28.

Докажите, что если a_i> 0, I = 1, 2,..., n, то

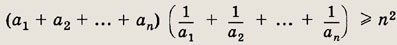
Задание 29.

Пусть x € [0; 1], i = 1, 2, ..., 2n. Найдите наименьшую величину выражения

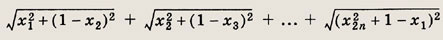
Ответ:

 

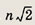
• Методом математической индукции часто достаточно просто доказываются утверждения, связанные с делимостью выражений.

В задачах 30—37 докажите, ч.то при любом натуральном n справедливы утверждения:

Задание 30.

n³ + 11n делится на 6

Решение:

Для n = 1 утверждение очевидно. Пусть оно выполняется для n = k. Докажем его справедливость для n = k + 1.

Положим A_k+1 = (k + 1)³ - 11(k + 1) и A_k — k³ - 11k. Поскольку A_k делится на 6, достаточно доказать, что разность A_k+1- A_k делится на 6. Но A_k+1- A_k = 3k²+ 3k + 12 - 3k(k + 1) + 12. Одно из двух чисел k или k + 1 — четное, поэтому 3k(k + 1) делится на 6, т. е. A_k+1- A_k делится на 6, что и требовалось доказать.

Задание 31.

Сумма кубов трех последовательных натуральных чисел делится на 9.

Задание 32.

n⁵ - n делится на 5

Задание 33.

4ⁿ + 15n - 7 делится на 9

Задание 34.

10ⁿ + 18n - 28 делится на 27

Задание 35.

7²ⁿ - 4²ⁿ делится на 33

Указание:

Примените формулу, приведенную в условии задачи 15, при а = 7² и b = 4².

Задание 36.

11ⁿ⁺² + 122²ⁿ⁺¹ делится на 133

Указание:

Если А_k = 11^k+2 + 12^2k+1, то A_k+1- A_k = 10A_k + 133 • 122^2k+1.

Задание 37.

20²ⁿ + 16²ⁿ - З²ⁿ - 1 делится на 323

Задание 38.

Докажите, что

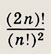
целое число, делящееся на (n + 1)

Решение:

Методом математической индукции устанавливаем

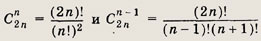
Так как это биномиальные коэффициенты, то они являются целыми числами. Далее, так как два последовательных натуральных числа n и n + 1 взаимно простые, то число п должно делить без остатка С_2n^n-1 . Тогда получаем, что число

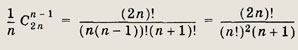
целое.

Задание 39.

Докажите, что если

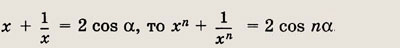
Указание:

Выражение

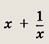
не может принимать значения, по модулю меньшие, чем 2. Равенство

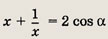
возможно в двух случаях:

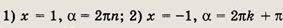
Задание 40.

Докажите, что расположенные в одной плоскости n прямых, из которых никакие две не параллельны и никакие три не пересекаются в одной точке, рассекают плоскость на

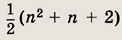
части.

2. Формула бинома Ньютона. Для любых целых чисел

называются биномиальными коэффициентами.

Задание 41.

Исходя из определения С_n^k , покажите, что справедливы формулы

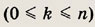
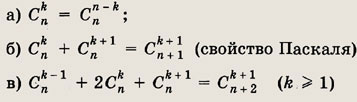
Решение:

Имеем

 

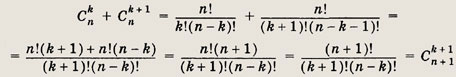
• Методом математической индукции можно доказать следующую формулу, называемую формулой бинома Ньютона:

(а + b)ⁿ = С_n⁰аⁿ+ C_n¹a^n-1b + C_n²a^n-2b² + ... + C_n^k a^n-kb^k + ... + C_nⁿbⁿ

Она справедлива для любых чисел а, b при любом натуральном n.

Слагаемое T_k = C_n^ka^n-k b^k, k = 0, 1, 2,..., n,

называется k-м членом разложения. (Отметим, что это (k + 1)-e слагаемое в правой части бинома.)

Задание 42.

Найдите следующие числа: С₅⁰ , С₅¹ , С₅² , С₇² , С₁₅² , C₁₅¹⁴ , C₁₅¹⁵ , C₁₀⁸

Ответ:

1; 5; 10; 21; 105; 15; 1; 45

Задание 43.

Используя формулу бинома Ньютона, запишите следующие разложения:

Ответ:

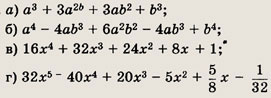
Задание 44.

Найдите n, если:

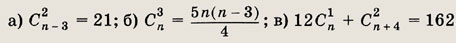
Решение а):

Так как

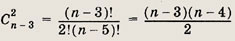
то задача сводится к решению квадратного уравнения

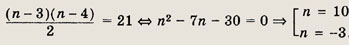
По смыслу задачи подходит только первый корень.

Ответ:

a) 10
б) 7
в) 8

Задание 45.

Упростите выражения:

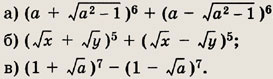
Решение а):

Применив формулу бинома Ньютона, имеем

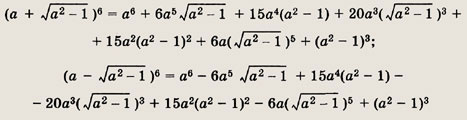
Сложив эти равенства, в правой части получим

2[a⁶ + 15а⁴(a² - 1) + 15а²(а² - 1)² + (а² - 1)³] = 2(32а⁶ - 48а⁴ + 18а² - 1).

Ответ:

a) 64а⁶ - 96a⁴ + З6а² - 2

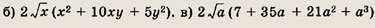
Задание 46.

В разложении

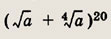
найдите слагаемое, содержащее а⁷.

Решение:

Используя формулу k-ro члена разложения бинома Ньютона, находим

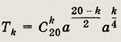
По условию,

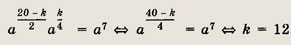
поэтому

Ответ:

125 970 a⁷

Задание 47.

В разложении

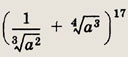
найдите слагаемое, не содержащее а.

Ответ:

T₈ = C₁₇⁸

Задание 48.

В разложении (х² + х - 4)ⁿ биномиальный коэффициент второго члена на 44 больше биномиального коэффициента первого члена. Найдите номер члена, не содержащего х.

Ответ:

Третий член (T₃).

Задание 49.

Сумма коэффициентов трех первых слагаемых разложения

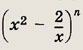
равна 97. Найдите член разложения, содержащий х⁴.

Ответ:

T₄ = 1120x⁴

Задание 50.

Найдите х, если известно, что второй член разложения бинома (х + x^{lg x})⁵ равен 106.

Ответ:

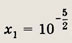
Задание 51.

Найдите х, если пятый член разложения бинома

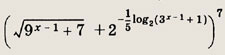
равен 84.

Ответ:

x₁ = 1, x₂ = 2

 

Используя формулу бинома, найдите следующие суммы (52—56):

Задание 52.

С_n⁰ +С_n¹ +С_n² + ... + С_nⁿ

Указание:

Запишите формулу бинома Ньютона (а + 6)ⁿ при а = b = 1.

Ответ:

2ⁿ

Задание 53.

С_n⁰ - C_n¹ + C_n² - C_n³ +... + (-1)ⁿC_nⁿ

Ответ:

0

Задание 54.

(С_n⁰)² + (С_n¹)² +... + (С_nⁿ)²

Решение:

Вычислим коэффициент при хⁿ в разложении (1 + х)²ⁿ. Он равен С_2nⁿ . С другой стороны,

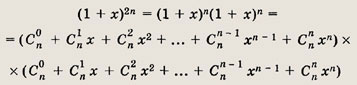
Перемножив эти скобки, выделим слагаемые, содержащие хⁿ:

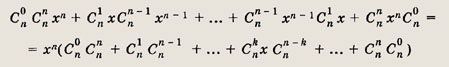
Так как С_n^k = С_n^k-1 (см. задачу 41), то в квадратных скобках записана сумма (С₀ⁿ)² + (С_n¹)² + ••• + (С„) , т. е. то выражение, которое требовалось вычислить, и оно равно С_2nⁿ .

Ответ:

С_2nⁿ

Задание 55.

C_n⁰C_m^k + C_n¹C_m^k-1 +... + C_n^kC_m⁰

Указание:

Вычислите коэффициент при х^k в выражениях (1 + х)^n+m + "' и (1 + х)ⁿ(1 + х)^m.

Ответ:

С^k_n+m

Задание 56.

С_n⁰+ 2C_n¹ + ЗC_n²+ ... + (n + 1)C_nⁿ

Указание:

Сложите первое и последнее слагаемые второе и предпоследнее и т.д.

Ответ:

(n + 2) • 2^n-1

 

3. Элементы комбинаторики. Понятие вероятности события.

1) Комбинации элементов, выбираемых из разных групп. Пусть имеется г различных групп элементов, из которых первая группа содержит n₁ различных элементов:

вторая — n₂ различных элементов: b₁

и т.д. до r-й группы, которая содержит n_r различных элементов:

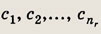
Выбираем по одному элементу из каждой группы и получаем комбинацию (выборку)

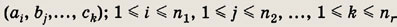
Число всех таких комбинаций равно N = n₁ • n₂ ... n_r. Примеры.

1. Подбрасывают игральный кубик, затем монету, наконец, из колоды, содержащей 52 различных карты, вытаскивают одну из карт. Сколько получится различных комбинаций?

Ответ: N = 6-2-52 = 624 комбинации.

2. Сколько трехзначных нечетных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?

Находим, что первая группа (цифры сотен) состоит из цифр 1, 2, 3, 4, 5, 6; вторая (цифры десятков) — из цифр 0, 1, 2, 3, 4, 5, 6; а третья (цифры единиц) — из 1, 3, 5. Таким образом, количество трехзначных нечетных чисел, составленное из указанных цифр, равно л = 6 • 7 • 3 = 126.

О т в е т: 126.

Отметим, что, если все г групп одинаковы, т. е. каждая состоит из одних и тех же различных между собой п элементов, то получаем выборки с повторениями. Число таких выборок ./V - n^r.

Пример.

Сколько различных трехзначных чисел можно составить из цифр 1, 3, 5, 7, 9?

О т в е т: N = 5³ = 125.

2) Выборка без повторений. Число размещений.

Пусть имеется n различных элементов а₁; a₂, ..., а_n. Выбираем один элемент и фиксируем его. Из оставшихся выбираем второй элемент и снова его фиксируем. Повторяя это действие

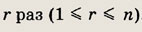
получим выборку

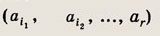
где индекс i₁ может принимать n различных значений, индекс i₂ — (n - 1) значение, ... , индекс i_r — (n - r + 1) значение. Число различных выборок

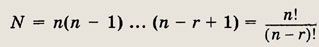
Это число обозначается символом А_n^r и называется числом размещений из n элементов по r элементов. При r = 0 полагаем А_n⁰ = 1.

Примеры.

1. Сколько трехзначных чисел можно записать цифрами 1 3, 5, 7, 9, если цифры записи чисел не повторяются?

О т в е т: N = А₅³ =5 • 4 • 3 = 60 чисел.

2. Сколькими способами можно рассадить 7 кроликов по 10 различным клеткам, если в каждую клетку сажают не более одного кролика?

О т в е т: А₁₀⁷ =10 • 9 • 8 • 7 • 6 • 5 • 4 = 604 800 способами.

3) Перестановки. Размещение из n по n элементов называется перестановкой и обозначается Р_n. Таким образом,

Р_n = A_nⁿ = n!

Пример.

Сколько пятизначных чисел можно составить из цифр 1, 3, 4, 5, 7, если в каждом из этих чисел ни одна из цифр не повторяется?

О т в е т: Р₅ = 5! = 120.

4) Сочетания. Пусть имеется n различных элементов а₁, а₂, .,., а_n. Любое r-элементное подмножество в этом множестве назовем сочетанием из n элементов по r элементов

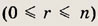
Число таких сочетаний обозначается символом С_n^r . Используя формулы для размещений
и перестановок, получаем

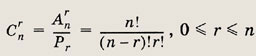
Примеры.

1. Сколько различных пятиэлементных подмножеств имеет множество, состоящее из 10 различных элементов?

О т в е т:

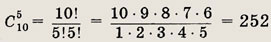
2. В урне имеется т белых и п черных шаров. Сколькими способами можно выбрать из урны r шаров, из которых будет k белых? (Считается, что шары одного цвета различны, например, пронумерованы.)
Находим, что из имеющихся m белых шаров можно выбрать k белых шаров С_m^k способами, а оставшиеся (r - k) черных шаров из п черных — С_n^r-k способами. Общее число способов C_m^kC_n^r-k.

О т в е т: C_m^kC_n^r-k.

5) Вероятность. Рассмотрим некоторый опыт, имеющий N взаимно исключающих друг друга равноправных исходов. Обозначим символом А некоторое событие, связанное с указанными исходами. Вероятностью Р(А) события А назовем число

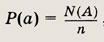
где ./V — общее число исходов рассматриваемого опыта, а N(A) — число исходов, приводящих к событию А.

Примеры.

1. Какова вероятность того, что наудачу выбранное двузначное число окажется нечетным и делящимся на 5 без остатка?

Так как общее число исходов опыта (выбор двузначного числа) равно 90, а число благоприятных исходов (выбор нечетного, делящегося на 5 числа) равно 9, то искомая вероятность равна

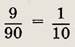
О т в е т: 0,1.

2. К перрону подали состав из 10 вагонов. За час до его отправки подошел первый пассажир и сел в один из вагонов. Через 5 мин подошел второй пассажир и сел наугад в один из вагонов. Через 5 мин подошел третий пассажир и, снова наугад, сел в один из вагонов и т.д., всего подошли 7 пассажиров. Какова вероятность того, что все они сели в разные вагоны?

Так как общее число исходов опыта (пассажиры садятся в вагоны) равно 10⁷, а число благоприятных исходов (все пассажиры сели в разные вагоны) равно А₁₀⁷, то искомая вероятность

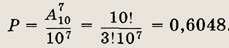
О т в е т: 0,6048.

Решите следующие задачи (57—77):

Задание 57.

Сколько различных делителей, включая 1 и себя, имеет число 2⁵ • З³ • 7⁴?

Решение:

Делитель числа 2⁵ • З³ • 7⁴ — это произведение делителей чисел 2⁵, З³ и 7⁴. Число 2⁵ имеет шесть делителей (1, 2, 2², 2³, 2⁴, 2⁵); З³ — четыре делителя; 7⁴ — пять делителей. Таким образом, искомое число делителей равно 6 • 4 • 5 = 120.

Ответ:

120

Задание 58.

Сколько диагоналей имеет выпуклый n-угольник?

Указание:

Каждую вершину можно соединить диагональю с n - 3 вершинами.

Ответ:

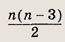
Задание 59.

Сколько различных семизначных чисел можно записать, используя цифры 3 и 5?

Ответ:

2⁷

Задание 60.

На одной из двух параллельных прямых лежат 15 точек, на другой — 9 точек. Сколько можно построить различных треугольников с вершинами в этих точках?

Решение:

Треугольник можно получить, выбрав две точки на первой прямой (С²₁₅ способами) и одну точку на второй прямой (С¹₉ способами) или выбрав одну точку на первой прямой (С¹₁₅ способами) и две точки на второй прямой (С²₉ способами). Общее число треугольников можно записать в виде С²₁₅ С¹₉ + С¹₁₅ + С²₉ = 1485.

Ответ:

1485

Задание 61.

Первенство страны по футболу проводится в два круга. Какое количество встреч следует провести, если первенство оспаривают 18 команд?

Ответ:

2C²₁₈= 306

Задание 62.

Двенадцать человек разбиты на три группы: 5 человек в первой группе, 4 — во второй и 3 — в третьей. Сколько может быть различных составов таких групп?

Ответ:

C⁵₁₂ С⁴₇ = 27 720

Задание 63.

Из 9 теннисисток и 6 теннисистов составляют три смешанные пары. Сколькими способами это можно сделать?

Решение:

Трех теннисисток из девяти можно выбрать С³₉ способами, а трех теннисистов из шести — С³₆ способами. Из выбранных трех теннисисток и трех теннисистов пары можно составить Р₃ способами. Таким образом, искомое число способов есть

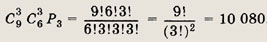
Ответ:

10 080

Задание 64.

Из 5 спортсменов и 10 спортсменок нужно составить команду так, чтобы в нее входили 2 спортсмена и 10 спортсменок. Сколькими способами это можно сделать?

Ответ:

C²₅ С³₁₀ = 1200

Задание 65.

Хоккейная команда состоит из 2 вратарей, 7 защитников и 10 нападающих. Сколькими способами тренер может образовать стартовую шестерку, состоящую из вратаря, двух защитников и трех нападающих?

Ответ:

C¹₂ С²₇С³₁₀ = 6480

Задание 66.

Сколько различных комбинаций букв можно получить из букв слова: а) школа; б) математика; в) Миссисипи?

Ответ:

Задание 67.

Из 16 бусинок: 6 зеленых, 5 белых, 2 красных и 3 голубых, составляют бусы. Сколько различных бус можно составить?

Решение:

Если бы мы раскладывали бусинки в ряд (не связывая в бусы), то было бы

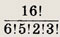
способов разложения. Если бусы разрывать в разных местах, то из одних бус можно получить 16 различных рядов из бусинок. Если при этом менять начало и конец каждого ряда, то можно получить еще 16 рядов. Таким образом, каждому экземпляру бус соответствует 32 разных ряда из бусинок.

Ответ:

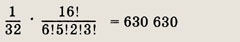
Задание 68.

По периметру круглой клумбы садовник высаживает 16 кустов роз — 6 кустов темно-красных, 5 кустов алых, 2 куста белых и 3 куста желтых. Сколькими различными способами он может это сделать?

Ответ:

1 261 260

Задание 69.

Из колоды, содержащей 52 карты (из них 4 туза), вынули 10 карт. В скольких случаях среди этих карт будет хотя бы один туз?

Указание:

Из общего количества наборов по 10 карт надо вычесть количество наборов по 10 карт из колоды с вынутыми из нее четырьмя тузами.

Ответ:

C¹⁰₅₂ С¹⁰₄₈

Задание 70.

Сколькими способами из колоды в 52 карты (из них 4 туза и 4 короля) можно вынуть 6 карт, содержащих ровно одного туза и ровно одного короля, причем одной масти?

Указание:

Тузы и короли одной масти можно выбрать четырьмя способами. Остальные 4 карты нужно выбрать из 44 карт.

Ответ:

4C⁴₄₄

Задание 71.

В урне 15 шаров: 10 белых и 5 черных. Какова вероятность того, что наугад вынутый из урны шар будет белым?

Решение:

Исходом назовем вынимание какого-нибудь шара. Всего исходов N = 15. Событие А — вынимание белого шара. Этому событию соответствует N(A) = 10 исходов. Вероятность события А есть

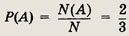
Ответ:

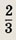
Задание 72.

Игральная кость подброшена дважды. Какова вероятность того, что:

а) оба раза выпала шестерка;

б) по одному разу выпали тройка и пятерка;

в) хотя бы один раз выпала единица?

Решение в):

Исход — результат подбрасывания двух кубиков. Всего исходов N = 36. «Не успешных» исходов (не выпала единица) — 25. Следовательно, имеется 36 - 25 = 11 успешных исходов (N(A) = 11).
Находим вероятность события

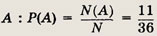
Ответ:

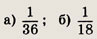
в)

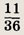
Задание 73.

Игральная кость подброшена дважды. Какова вероятность того, что сумма выпавших очков равна 9?

Ответ:

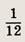
Задание 74.

Брошены три игральные кости. Найдите вероятность следующих событий:

а) на каждой из выпавших граней появится шестерка;

б) на всех выпавших гранях появится одно и то же четное число;

в) хотя бы на одной из выпавших граней появится пятерка;

г) ни на одной грани не будет двойки;

д) выпавшие на гранях числа образуют геометрическую прогрессию со знаменателем, отличным от единицы.

Ответ:

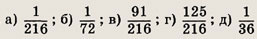
Задание 75.

На складе имеется 100 деталей, из которых 10 бракованные. Наугад выбирают две детали. Какова вероятность того, что обе детали не бракованные?

Ответ:

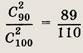
Задание 76.

В экзаменационный билет входят три вопроса программы, состоящей из 50 вопросов. Абитуриент не знает 20 вопросов программы. Какова вероятность того, что он вытянет билет, где все вопросы ему известны?

Ответ:

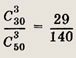
Задание 77.

Из вазы, где стоят 10 красных и 5 белых гвоздик, наугад выбирают 4 цветка. Какова вероятность того, что среди выбранных цветов окажется 2 красные и 2 белые гвоздики?

Ответ:

 

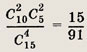
В следующих задачах на «геометрические вероятности» вероятность события А трактуется как отношение «площади» фигуры, приводящей к событию Л, к «площади» фигуры всего пространства событий.

Пример.

В круг радиуса R помещен меньший круг радиуса r. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет в малый круг (предполагается, что вероятность попадания в круг пропорциональна площади круга и не зависит от его расположения).

Из условия примера следует, что событие А состоит в попадании в малый круг, все пространство событий — попадание в большой круг. Поэтому

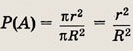
О т в е т:

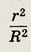
Задание 78.

Точка брошена в круг радиуса R. Какова вероятность того, что она попадет внутрь вписанного в круг правильного n-угольника?

Ответ:

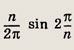
Задание 79.

В квадрате

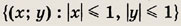
наугад выбирают точку А(х; у). Какова вероятность того, что

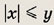
Указание:

Искомая вероятность — отношение площади заштрихованной фигуры к площади квадрата.

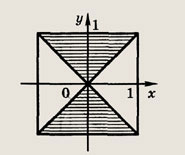
Ответ:

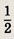
Задание 80.

В прямоугольнике

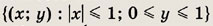
выбирают наугад точку А(х; у). Какова вероятность того, что х² < у ?

Указание:

Площадь заштрихованной фигуры равна

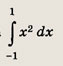
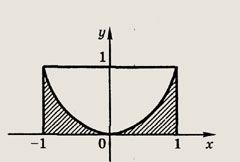
Ответ:

Задание 81.

В квадрате

наугад выбирают точку А(р; q). Какова вероятность того, что корни уравнения х² + рх + q = 0 окажутся действительными и имеющими один и тот же знак?

Решение:

Условие того, что квадратное уравнение имеет два корня одного знака, описывается системой

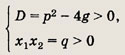
Искомая вероятность — отношение площади заштрихованной фигуры

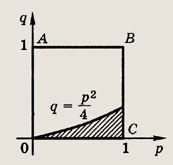
равной

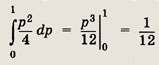
к площади квадрата ОАВС (S_OABC = 1).

Ответ:

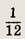
Задание 82.

На окружности радиуса R наудачу поставлены точки А, В и С. Найдите вероятность того, что треугольник ABC будет остроугольным.

Решение:

Расположим декартову систему координат так, что начало координат совпадало с центром круга, а точка А лежала на оси Ох.

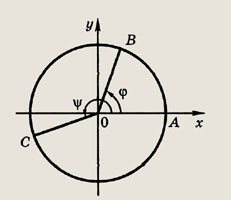
Через

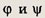
обозначим углы, которые образуют лучи ОВ и ОС с положительным направлением оси Ох, причем углы отсчитываются от этой оси против часовой стрелки. Углы

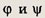
принимают любые значения, принадлежащие отрезку

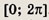
Рассмотрим плоскость

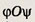
Чтобы треугольник ABC был остроугольным, надо:

1) чтобы один из углов

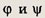
принадлежал интервалу

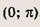
а другой — интервалу

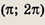
2)

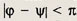
На рис. 12.4, б это множество заштриховано. Необходимо найти отношение площадей заштрихованного множества к площади квадрата OPQR.

Ответ:

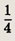
Задание 83.

Наудачу взяли два положительных числа х и у, каждое из которых не превосходит 2. Найдите вероятность того, что

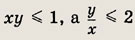
Указание:

Площадь заштрихованной фигуры можно вычислить так:

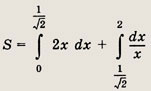
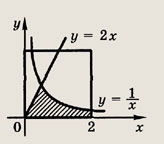
Ответ:

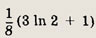
Задание 84.

Двое договорились о встрече в определенном месте между 9 и 10 часами утра, причем пришедший первым ждет второго в течение 15 мин, после чего уходит. Найдите вероятность того, что встреча состоится, если каждый из них обязательно придет на место встречи в произвольный момент между 9 и 10 часами утра.

Указание:

Надо найти площадь той части квадрата

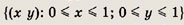
координаты точек которой удовлетворяют соотношению

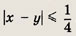
Ответ:

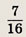
Задание 85.

За круглый стол садятся случайным образом 8 мужчин и 8 женщин. Какова вероятность того, что никаких двое мужчин и никакие две женщины не сядут рядом?

Ответ:

 

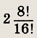
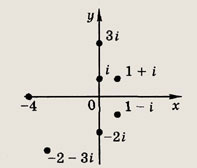
4. Комплексные числа. Комплексным числом называется упорядоченная пара действительных чисел: z = (x; у) или 2 = х + iy. Если действительные числа удобно отождествлять с точками на прямой, то комплексные — с точками на плоскости: числу z = х + iy ставится в соответствие точка с координатами х и у. При этом число х называется действительной частью комплексного числа z (х = Rez), ay — мнимой частью z (у = Imz).

Изобразите на комплексной плоскости следующие комплексные числа (86—95):

Задание 86.

i

Ответ:

Задание 87.

3i

Ответ:

Задание 88.

-4

Ответ:

Задание 89.

-2i

Ответ:

Задание 90.

1 + i

Ответ:

Задание 91.

1 - i

Ответ:

Задание 92.

-2 - 3i

Ответ:

Задание 93.

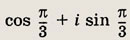
Ответ:

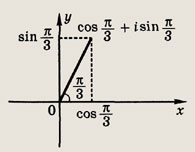
Задание 94.

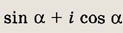
Ответ:

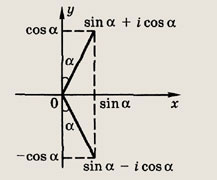
Задание 95.

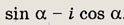
Ответ:

 

С комплексными числами можно совершать арифметические действия.

Пусть

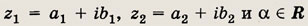
— действительное число; тогда имеют место равенства:

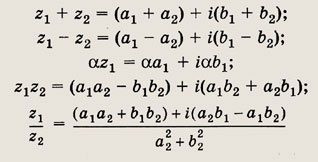
Выполните указанные действия (96—113):

Задание 96.

(2 + 3i) + (3 + 4i)

Ответ:

5 + 7i

Задание 97.

(2 + 3i) - (i + 1)

Ответ:

1 + 2i

Задание 98.

(2 - i)(2 + i)

Ответ:

5

Задание 99.

(3 - i)(2 + i)

Ответ:

7 + i

Задание 100.

(2 + 3i)(3 - 2i) + (2 - 3i)(3 + 2i)

Ответ:

24

Задание 101.

(1 - 3i)(2 + i) - (2 - i)(1 + 3i)

Ответ:

- 10i

Задание 102.

Ответ:

2 + 2i

Задание 103.

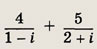
Ответ:

4 + i

Задание 104.

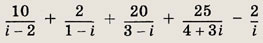
Ответ:

7

Задание 105.

(1 + i)³

Ответ:

-2 + 2i

Задание 106.

i¹⁷

Решение:

i¹⁷ = (i⁴)(i⁴)(i⁴)(i⁴)i, где i⁴ = (i²)² = (-1)² = 1.

Ответ:

i

Задание 107.

i^-5

Ответ:

-i

Задание 108.

(-i)²⁰⁰⁰

Ответ:

1

Задание 109.

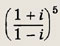
Ответ:

i

Задание 110.

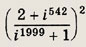
Ответ:

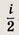
Задание 111.

(1 - i)³ + (1 + i)³

Ответ:

-4

Задание 112.

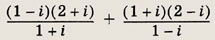
Ответ:

2

Задание 113.

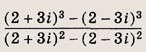
Ответ:

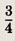
Найдите действительные числа х и г/, если справедливы заданные равенства (114—115):

Задание 114.

Зх - у + (х + y)i = 1 + 5i

Решение:

Комплексные числа равны, если равны их действительные и мнимые части. В данном случае

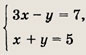
откуда находим значения х и у.

Ответ:

х = 3; у = 2

Задание 115.

(1 + i)x - (1 - i)y = 3 - i

Ответ:

x = 1; у= -2

 

• Числа а и b являются декартовыми координатами точки, соответствующей комплексному числу z = а + ib. Ту же точку можно задать с помощью полярных координат

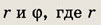
— расстояние от точки z до начала координат, а

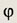
— угол между положительным направлением оси Ох и радиус-вектором Oz, отсчитываемый против часовой стрелки .

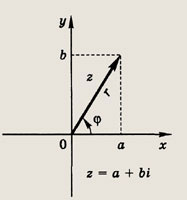
Число r называется модулем числа z (r = |z|), а угол

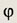
— аргументом

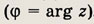
При этом

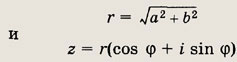
Последнее равенство называется тригонометрической формой записи комплексного числа.

Определите модуль комплексного числа (116—125):

Задание 116.

1 + i

Ответ:

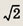
Задание 117.

4 + Зi

Ответ:

5

Задание 118.

-4i

Ответ:

4

Задание 119.

-2 - i

Ответ:

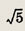
Задание 120.

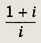
Ответ:

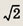
Задание 121.

(3 - i)²

Ответ:

10

Задание 122.

(1 + i)⁴ + Зi

Ответ:

5

Задание 123.

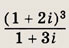
Ответ:

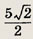
Задание 124.

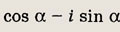
Ответ:

1

Задание 125.

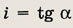
Ответ:

 

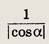
Определите аргумент комплексного числа (126—135). Для определенности считайте, что

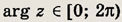
Задание 126.

3

Ответ:

0

Задание 127.

i

Ответ:

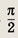
Задание 128.

-Зi

Ответ:

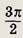
Задание 129.

0

Ответ:

Аргумент не определен

Задание 130.

-2

Ответ:

Задание 131.

1 + i

Ответ:

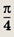
Задание 132.

1 -i

Ответ:

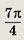
Задание 133.

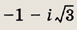
Ответ:

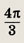
Задание 134.

4 + Зi

Ответ:

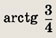
Задание 135.

-1 + 2i

Ответ:

 

Запишите в тригонометрической форме следующие комплексные числа (136—149):

Задание 136.

1 - i

Ответ:

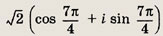
Задание 137.

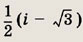
Ответ:

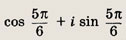
Задание 138.

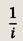
Ответ:

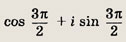
Задание 139.

3 - 4i

Ответ:

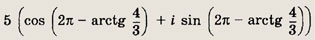
Задание 140.

-5 + 12i

Ответ:

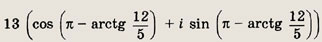
Задание 141.

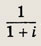
Ответ:

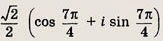
Задание 142.

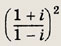
Ответ:

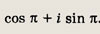
Задание 143.

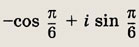
Ответ:

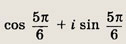
Задание 144.

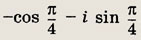
Ответ:

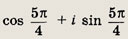
Задание 145.

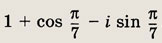
Решение:

Находим модуль числа:

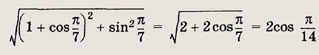
Тогда данное число примет вид

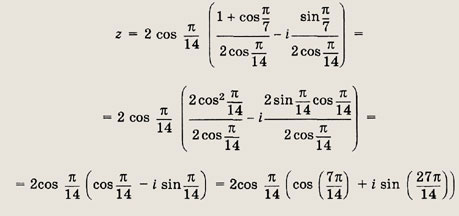
Ответ:

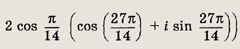
Задание 146.

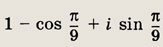
Ответ:

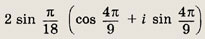
Задание 147.

Ответ:

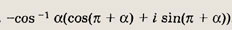
Задание 148.

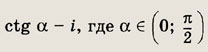
Ответ:

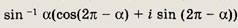
Задание 149.

Ответ:

 

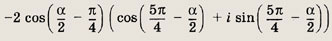
При решении задач 150, 151 используйте тригонометрическую форму записи комплексных числел z₁ и z₂:

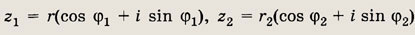
Задание 150.

Докажите, что:

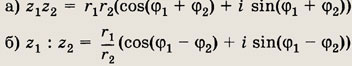
Решение а):

Имеем

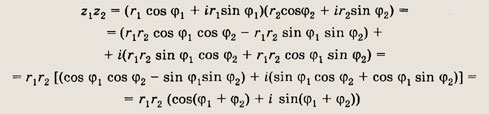
Задание 151.

Докажите формулу Муавра:

(cos х + i sin x)ⁿ = cos nx + i sin nx.

Указание:

Воспользуйтесь методом математической индукции и результатом задачи 150

 

Выполните указанные действия (152—154):

Задание 152.

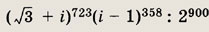
Решение:

Запишем числа

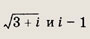
в тригонометрической форме:

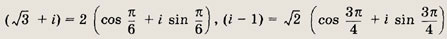
Теперь по формуле Муавра находим

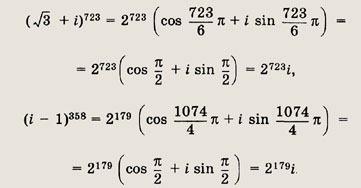
Итак, искомое произведение равно 2⁷²³i • 2¹⁷⁹i • 2^-900 = 4(i)² = -4.

Ответ:

-4

Задание 153.

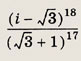
Ответ:

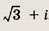
Задание 154.

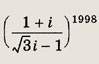
Ответ:

 

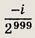
• Корнем n-й степени из комплексного числа

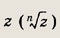
называется число, n-я степень которого равна

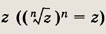
У любого отличного от нуля комплексного числа существует ровно n корней n-й степени, которые можно определить по формуле

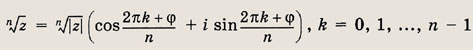
где

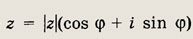
— данное комплексное число,

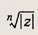
— арифметический корень n-й степени из действительного числа |z|. На комплексной плоскости корни n-й степени представляют собой вершины правильного n-угольника.

Вычислите значения корней и изобразите их на комплексной плоскости (155—166):

Задание 155.

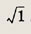
Решение:

Так как 1 = l(cos 0 + i sin 0), то

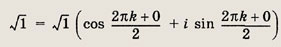
где k = 0; 1. При k = 0 получаем 1(cos0 + isin0) = 1; при k = 1 находим 1(cos П + i sin П ) = -1.

Ответ:

{±1}

Задание 156.

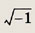
Ответ:

{±i}

Задание 157.

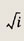
Ответ:

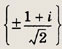
Задание 158.

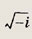
Ответ:

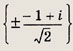
Задание 159.

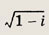
Указание:

Тригонометрическая
форма записи корней имеет вид

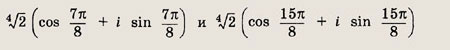
Для нахождения значений полученных тригонометрических функций воспользуйтесь формулами

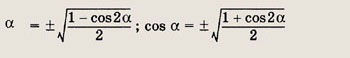
Ответ:

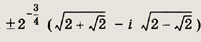
Задание 160.

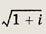
Ответ:

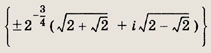
Задание 161.

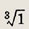
Ответ:

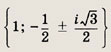
Задание 162.

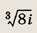
Ответ:

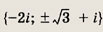
Задание 163.

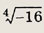
Ответ:

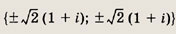
Задание 164.

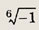
Ответ:

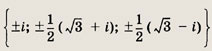
Задание 165.

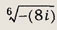
Ответ:

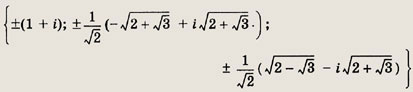
Задание 166.

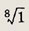
Ответ:

 

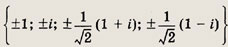
Решите уравнения (167—179):

Задание 167.

z² + 2z + 3 = 0

Решение:

По формуле корней квадратного уравнения находим

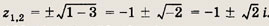
Ответ:

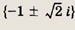
Задание 168.

z² - 2z + 2 = 0

Ответ:

{1 ± i}

Задание 169.

z² = -z

Ответ:

{0; -1}

Задание 170.

(z - i)² = (2 + i)²

Указание:

Примените формулу разности квадратов.

Ответ:

0

Задание 171.

z³ - 64 = 0

Указание:

z³ - 64 = (z - 4)(z² + 4z + 16).

Ответ:

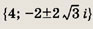
Задание 172.

z³ = i

Ответ:

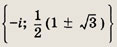
Задание 173.

z⁴ = i

Ответ:

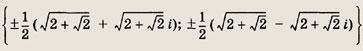
Задание 174.

2z² + |z| = 0

Решение:

Пусть z = х + iy. Уравнение имеет вид

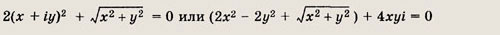
откуда

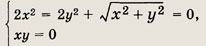
Решениями данной системы являются три пары чисел (0; 0),

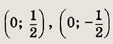
Ответ:

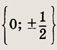
Задание 175.

z⁴ + 5z + 4 = 0

Ответ:

{±i; ±2i}

Задание 176.

(z² - z)² + 2(z² - 2) + 5 = 0

Ответ:

{-1 ± 2i; -1 + i}

Задание 177.

(z²- z - 1)(z² - z - 2) = 12

Ответ:

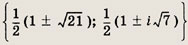
Задание 178.

z³ - 3z² + 3z - 3 = 0

Указание:

Данное уравнение можно записать так: (z - 1)³ = 2.

Ответ:

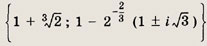
Задание 179.

(z + 2)(z + 1)(z - 1)(z - 2) = 9

Ответ:

 

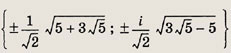
Изобразите на комплексной плоскости геометрические места точек, заданные следующими соотношениями (180—198):

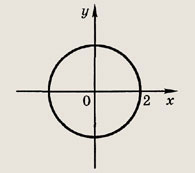
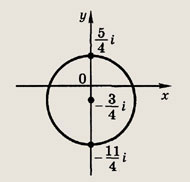
Задание 180.

|z| = 2

Ответ:

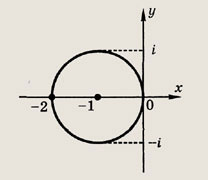
Задание 181.

|z + 1| = 1

Указание:

|z - (-1)| = 1. Требуется найти точки z, удаленные от точки (-1) на 1.

Ответ:

Задание 182.

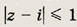
Ответ:

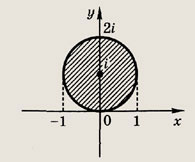
Задание 183.

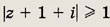
Ответ:

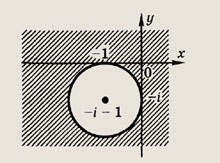
Задание 184.

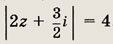
Ответ:

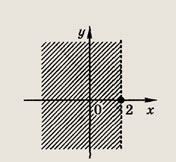
Задание 185.

Rez < 2

Ответ:

Задание 186.

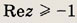
Ответ:

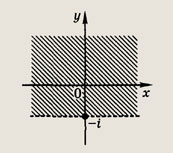
Задание 187.

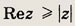
Ответ:

Положительная полуось

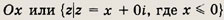
Задание 188.

-3 < Rez < 0

Ответ:

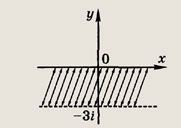
Задание 189.

Ответ:

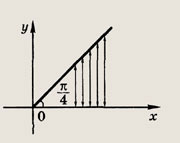
Задание 190.

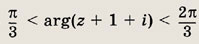
Указание:

Множество точек z таких, что

нужно сдвинуть на 1 вниз и на 1 влево.

Ответ:

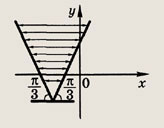
Задание 191.

|z - i| + |z + i| = 2

Указание:

Требуется найти множество точек z, сумма расстояний от которых до точек i и -i равно 2.

Ответ:

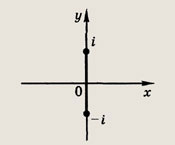
(отрезок [-i; i] на мнимой оси Оу).

Задание 192.

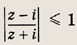
Ответ:

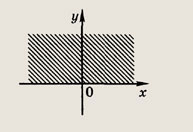
Задание 193.

Ответ:

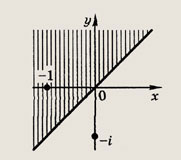
Задание 194.

Ответ:

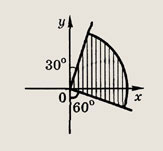
Задание 195.

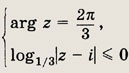
Ответ:

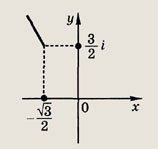
Задание 196.

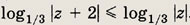
Ответ:

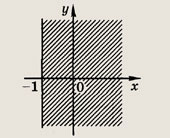
Задание 197.

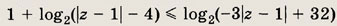
Ответ:

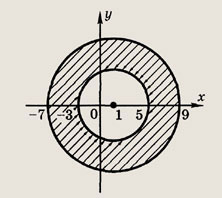
Задание 198.

cos |z| < 0

Ответ:

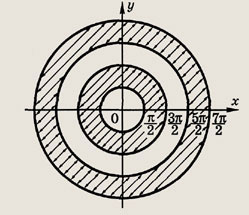
Задание 199.

При каких р и q уравнение z⁴ + pz² + q = 0:

а) имеет только действительные корни;

б) не имеет действительных корней;

в) имеет чисто мнимые корни?

Ответ:

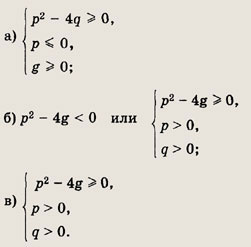
Задание 200.

Найдите наименьшее значение |z|, если |z + 2 - 2i| = 1.

Ответ:

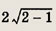
Задание 201.

Найдите положение третьей вершины равностороннего треугольника, если две его вершины находятся в точках z₁ = 5 + i, z₂ = 1 + 5i.

Ответ:

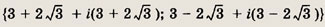
Задание 202.

Три точки z₁ = 1 + i; z₂ = 1 + 4i; z₃ = 4 + 4i являются вершинами параллелограмма. Найдите положение
четвертой вершины.

Ответ:

{4 + i; 4 + 7i; -2 + i}