Старший и верхний центральный показатели линейной системы
alt="Старший и верхний центральный показатели линейной системы" width="64" height="32" align="BOTTOM" border="0" />; значит,
 .
.
2) если
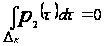 ,
то
,
то
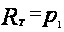 ;
значит,
;
значит,
 .
.
если
 ,
то
,
то
 ;
значит,
;
значит,
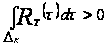 .
.
Таким образом,
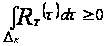 .
.
2.Докажем, что
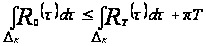 .
.
Очевидно,
что
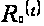 ─
функция ограниченная
и
─
функция ограниченная
и
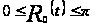 .
.
Отсюда следует, что
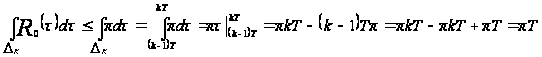 ,
,
то есть
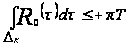 ,
,
Так как
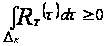 ,
,
то
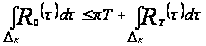 .
.
3.Докажем, что
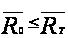 для любого
для любого
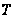 .
.
По определению
1.6 вычислим
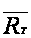 ,
используя
утверждение
1.2:
,
используя
утверждение
1.2:
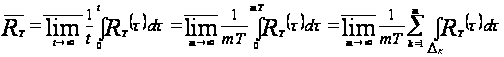 .
.
По определению
1.6 вычислим
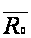 ,
используя
утверждение
1.2:
,
используя
утверждение
1.2:
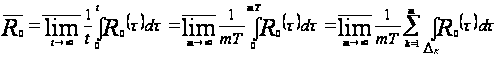 .
.
Теперь рассмотрим
все возможные
случаи расположений
отрезков
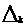 по отношению
к отрезкам
по отношению
к отрезкам
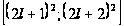 и
и
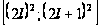 .
.
I. Если
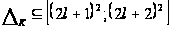 ,
где
,
где
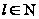 ,
то
,
то
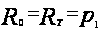 ,
,
следовательно,
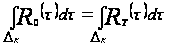 ;
;
II. если
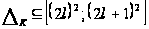 ,
где
,
где
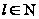 ,
то
,
то
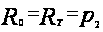 ,
,
следовательно,
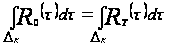 ;
;

III. если
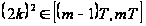 ,
,
то
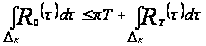 ;
;
IV. если
 ,
,
то
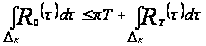 ;
;
Для каждого
 найдется такое
найдется такое
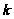 ,
что выполняется
,
что выполняется
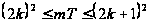 .
.
Тогда
 ;
;
Для каждого
 найдется такое
найдется такое
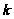 ,
что выполняется
,
что выполняется
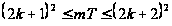 .
.
Тогда
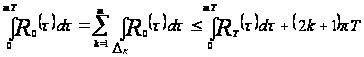 .
.
Из вышеперечисленных случаев 1) и 2) следует, что
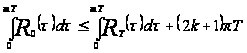 , (**)
, (**)
для любого
 такого, что
такого, что
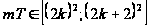 ,
,
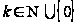 .
.
Учитывая
неравенство
(**), перейдем к
непосредственному
доказательству
неравенства
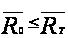 :
:
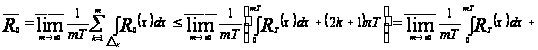
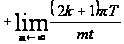 .
.
Теперь оценим
выражение
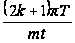 .
.
Очевидно, выполняется следующее неравенство:
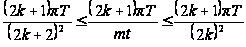 .
.
Перейдем к пределам:
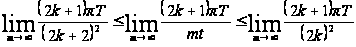 ,
,
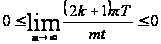 .
.
Следовательно,
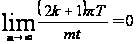 .
.
Значит,
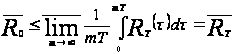 ,
,
то есть для
любого
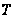
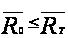 .
.
По определению 1.11
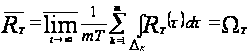 .
.
Таким образом,
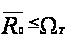 для любого
для любого
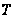 .
.
По замечанию 1.4 получаем, что
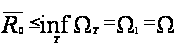 .
.
Следовательно,
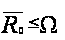 .
.
Так как мы
доказали, что
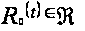 (P),
то есть
(P),
то есть 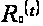 -
верхняя функция
для семейства
P, то, опираясь
на определение
1.9, получаем, что
-
верхняя функция
для семейства
P, то, опираясь
на определение
1.9, получаем, что
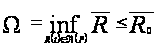 ,
,
то есть
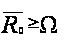 .
.
А значит,
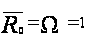 .
.
Итак, в этом разделе был рассмотрен случай
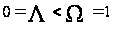 .
.
5. ОСНОВНЫЕ СВОЙСТВА ВЕРХНЕГО ЦЕНТРАЛЬНОГО ПОКАЗАТЕЛЯ
Р.Э. Виноград
ввел[5] понятие
верхнего центрального
показателя
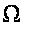 системы
системы
 .
(1)
.
(1)
Переход от невозмущенной системы (1) к возмущенной системе
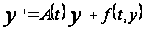
сопровождается
изменением
показателей.
Верхний центральный
показатель
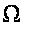 системы (1) и
характеризует
это изменение
в определенном
классе возмущений.
Имеет место
теорема Р.Э.
Винограда.
системы (1) и
характеризует
это изменение
в определенном
классе возмущений.
Имеет место
теорема Р.Э.
Винограда.
Теорема
[2,с.164-166;3]. Для любого
 можно указать
можно указать
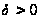 ,
что при любых
непрерывных
возмущениях
,
что при любых
непрерывных
возмущениях
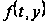 ,
,
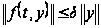 ,
,
будут выполняться неравенства
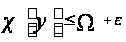 .
.
В.В. Миллионщиковым доказано, что последняя оценка неулучшаема, а именно
Теорема [4].
Для любого
 найдется возмущение
найдется возмущение
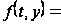 Qe
Qe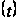
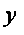 ,
||Qe
,
||Qe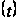 ||
||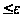 ,
,
такое, что система
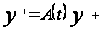 Qe
Qe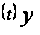
имеет решение
 ,
для которой
,
для которой
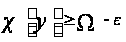 .
.
Значит, для
рассмотренной
в дипломной
работе системы
наиболее быстро
растущими
решениями
«руководит»
показатель
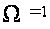 ,
а не показатель
,
а не показатель
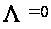 .
.
ЗАКЛЮЧЕНИЕ
В данной
дипломной
работе рассматриваются
соотношения
между старшим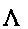 и
верхним
центральным
и
верхним
центральным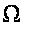 показателями
линейной системы
показателями
линейной системы
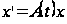
с кусочно непрерывными ограниченными коэффициентами.
Показано,
что существует
два различных
случая отношений
между старшим
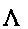 и верхним центральным
и верхним центральным
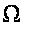 показателями
линейных систем:
показателями
линейных систем:
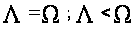 .
На примере
заданной линейной
однородной
диагональной
системы дифференциальных
уравнений
подробно рассмотрены
вычисления
характеристического
показателя
Ляпунова, спектра,
старшего и
верхнего центрального
показателей.
.
На примере
заданной линейной
однородной
диагональной
системы дифференциальных
уравнений
подробно рассмотрены
вычисления
характеристического
показателя
Ляпунова, спектра,
старшего и
верхнего центрального
показателей.
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Б.П. Демидович, Лекции по математической теории устойчивости.-
Москва, «Наука», 1967г.
2. Б.Ф. Былов, Р.Э. Виноград, Д.М. Гробман, В.В. Немыцкий, Теория
показателей Ляпунова и ее приложения к вопросам устойчивости.- Москва, «Наука», 1966г.
3. Р.Э. Виноград, Оценка скачка старшего характеристического
показателя при малых возмущениях.-Докл. АН СССР, 1957г., т.114, №3, с.459-461.
4. В.М. Миллионщиков, Доказательство достижимости центральных показателей линейных систем.- Сиб. мат.ж., 1969г., т.10, №1, с.99-104.
5. Р.Э. Виноград, О центральном характеристическом показателе системы дифференциальных уравнений.- Матем.сб., 1957г., т.42(84), С.207-222.
