Формулы по математическому анализу
Формулы дифференцирования Таблица основных интегралов
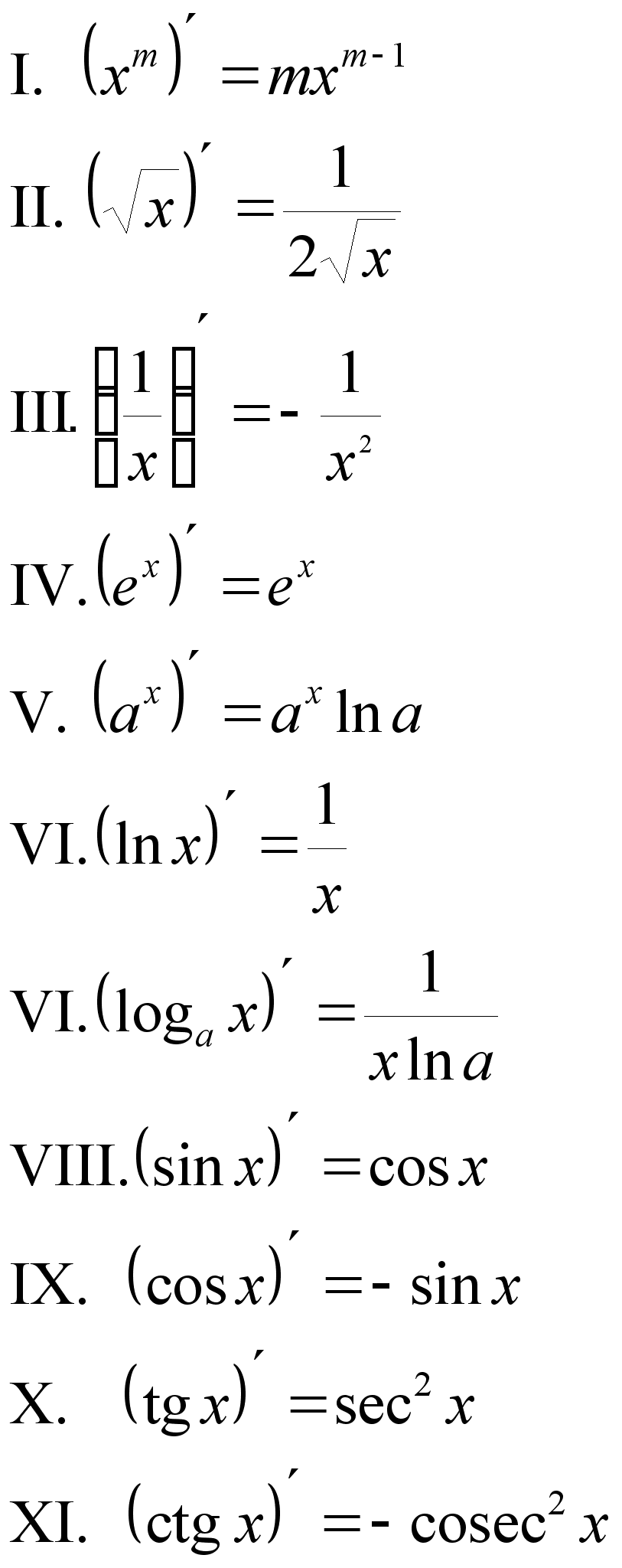
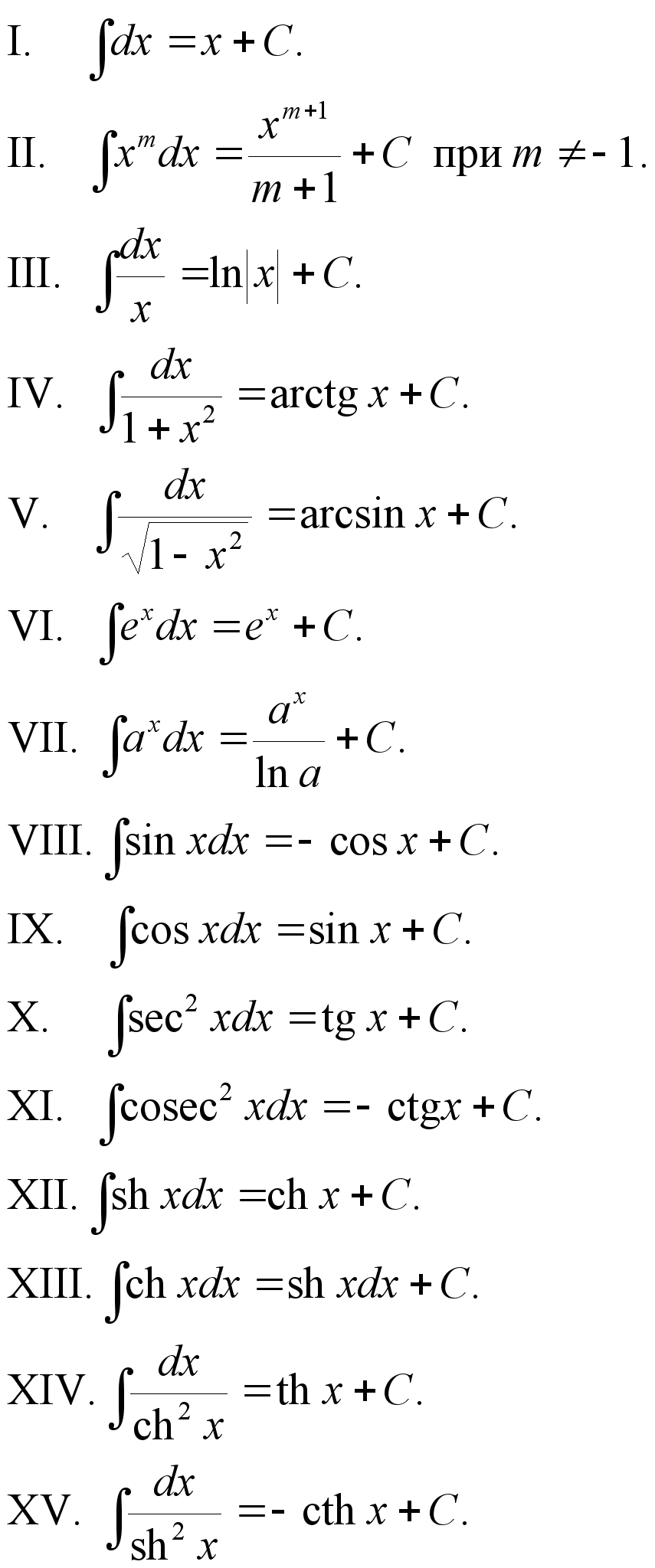
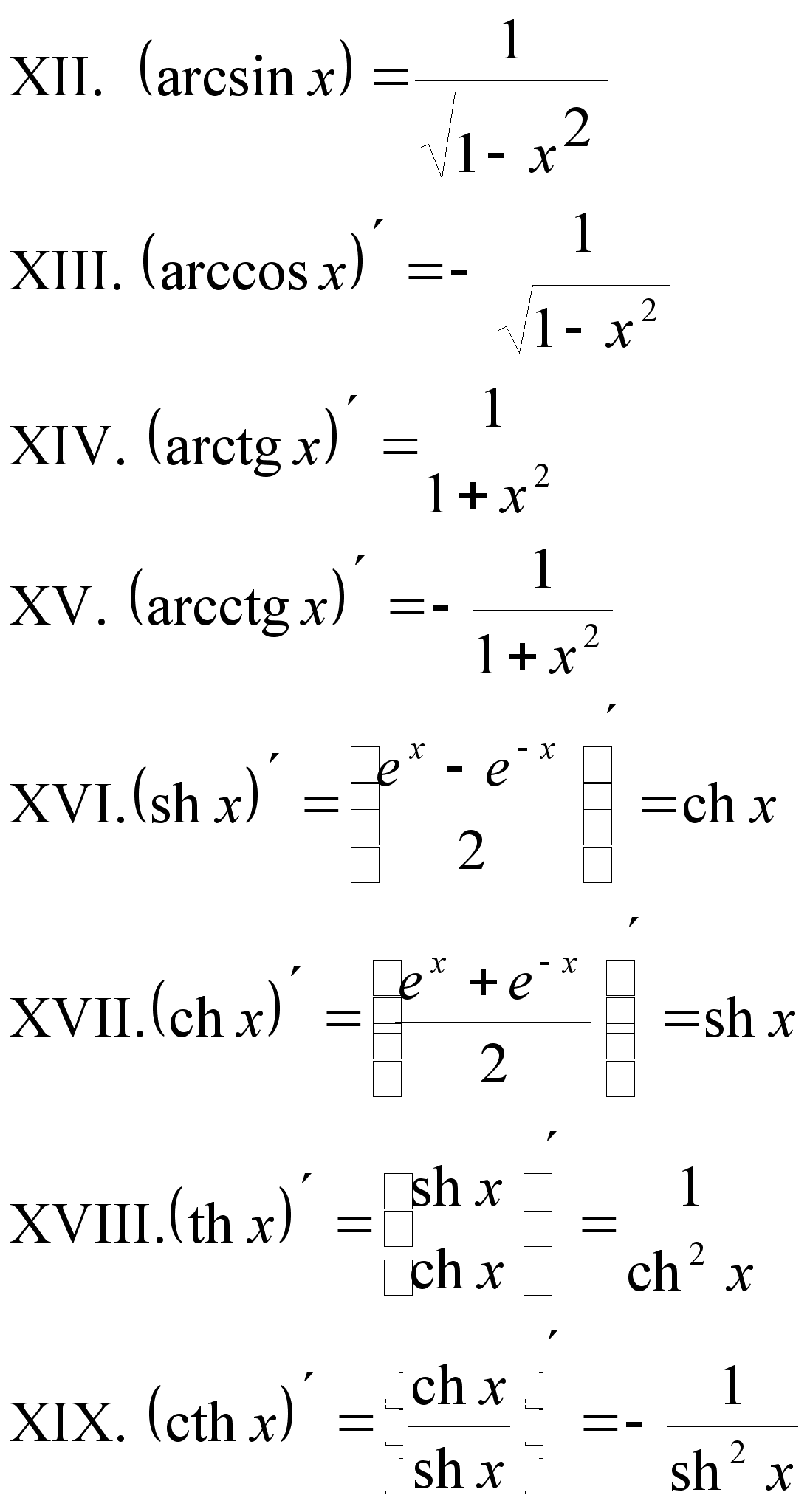
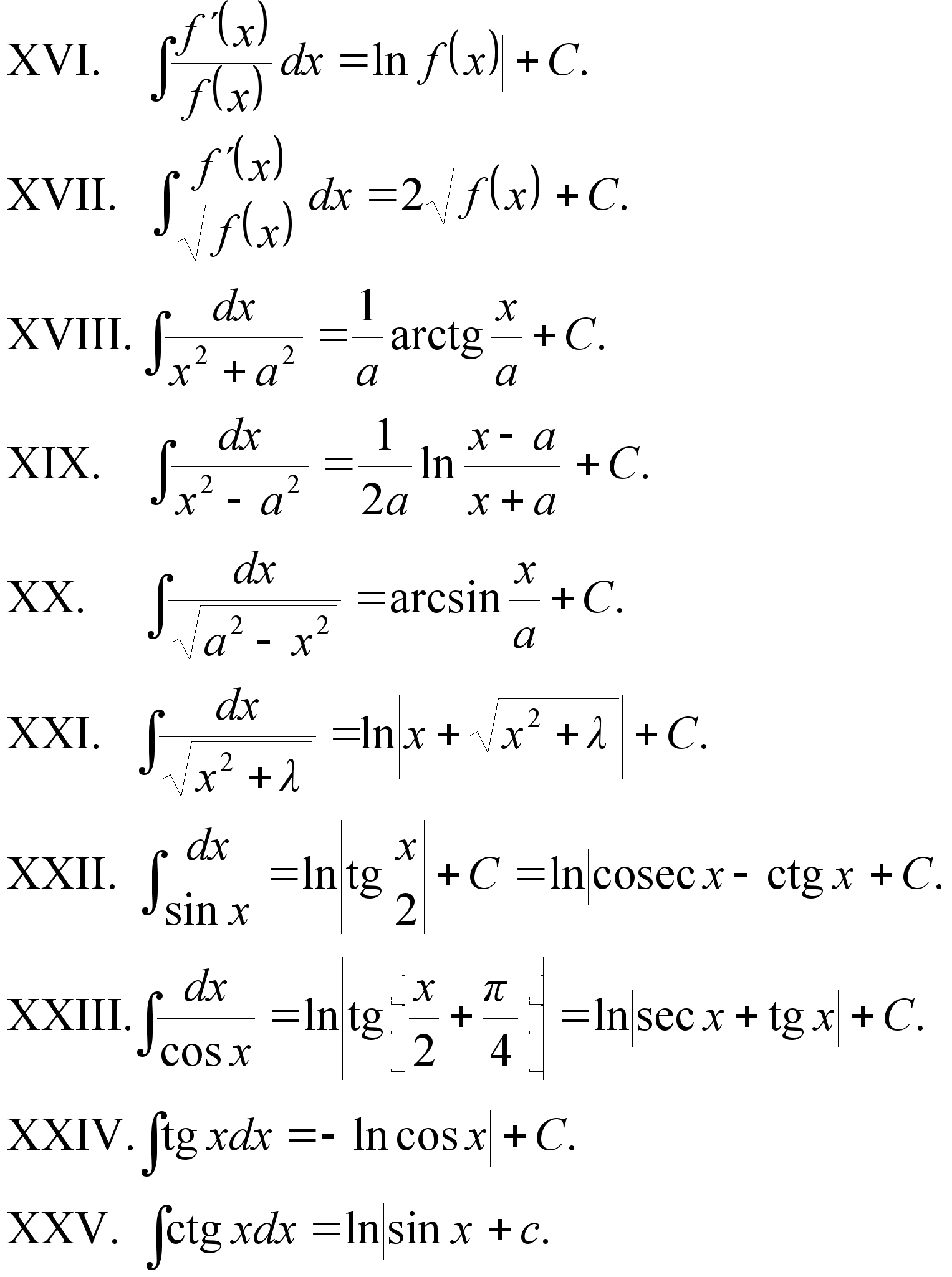
Правила интегрирования
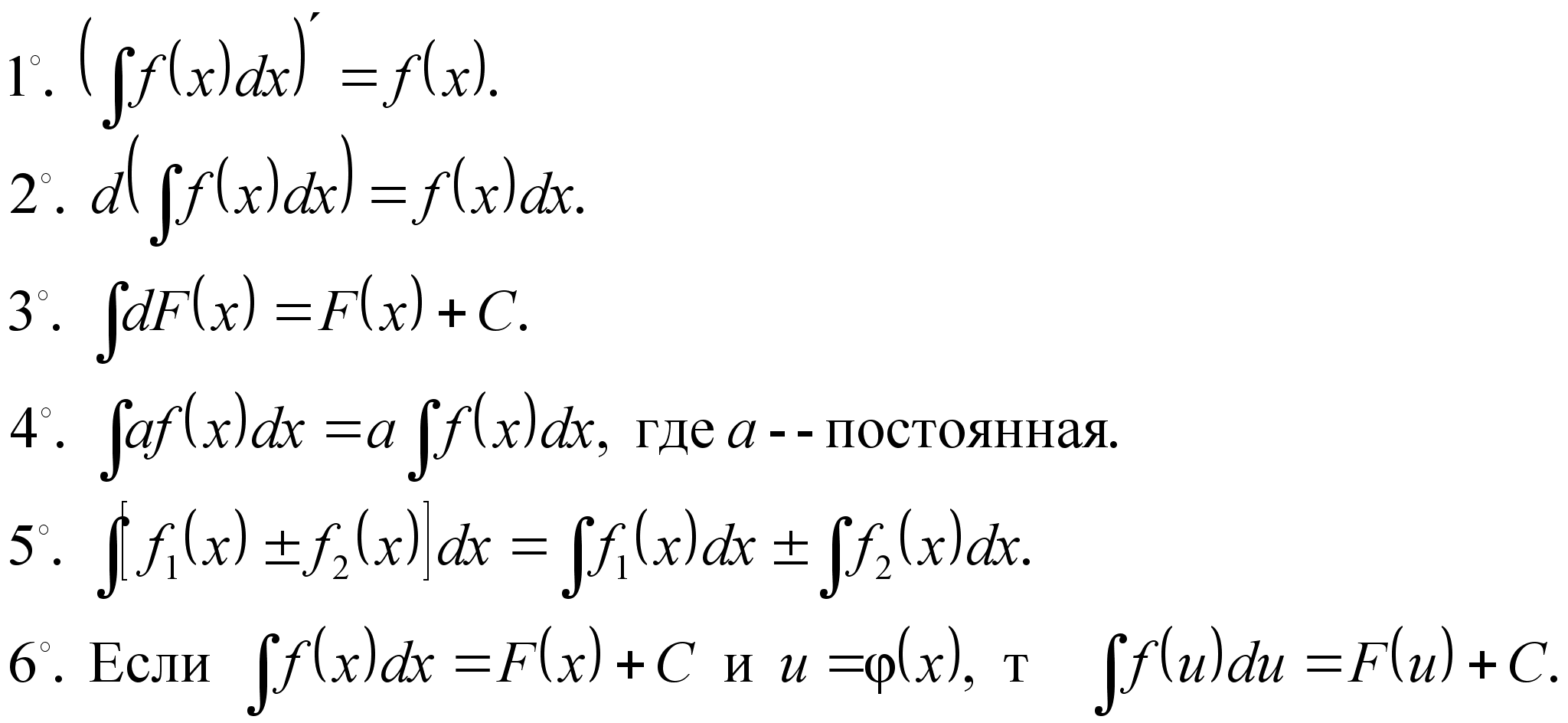
Основные правила дифференцирования
Пусть С—постоянная, u=u(x), v=v(x) – функции, имеющие
производные.
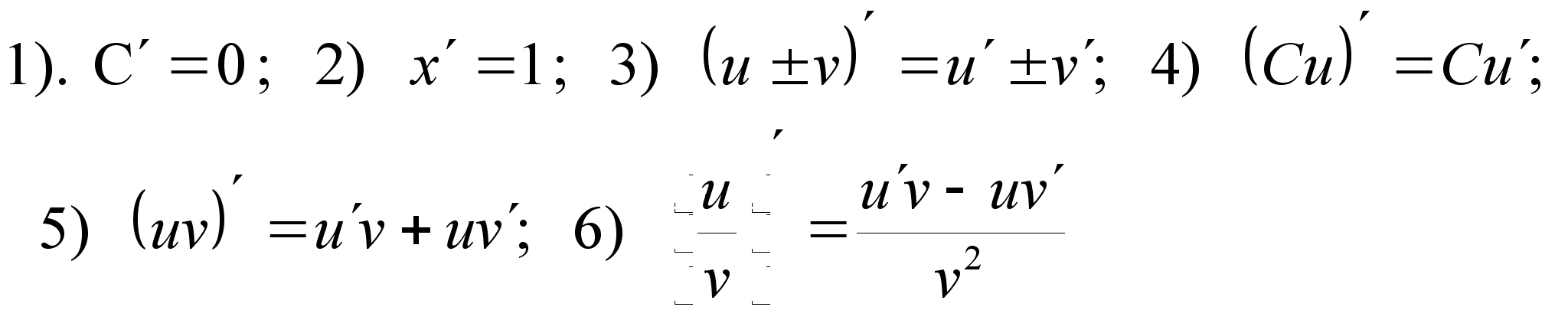
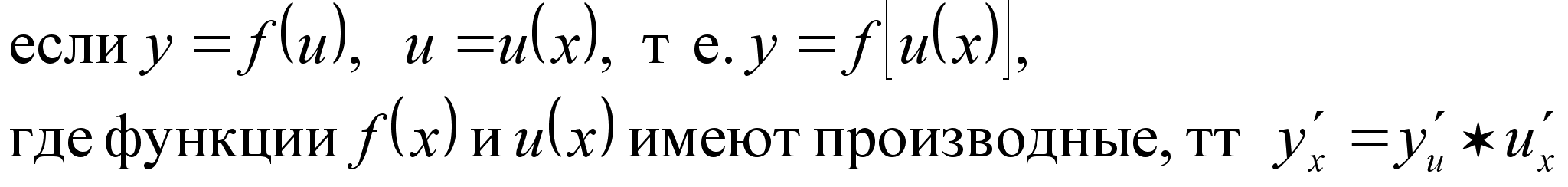
7)

Интегрирование по частям Основные свойства
о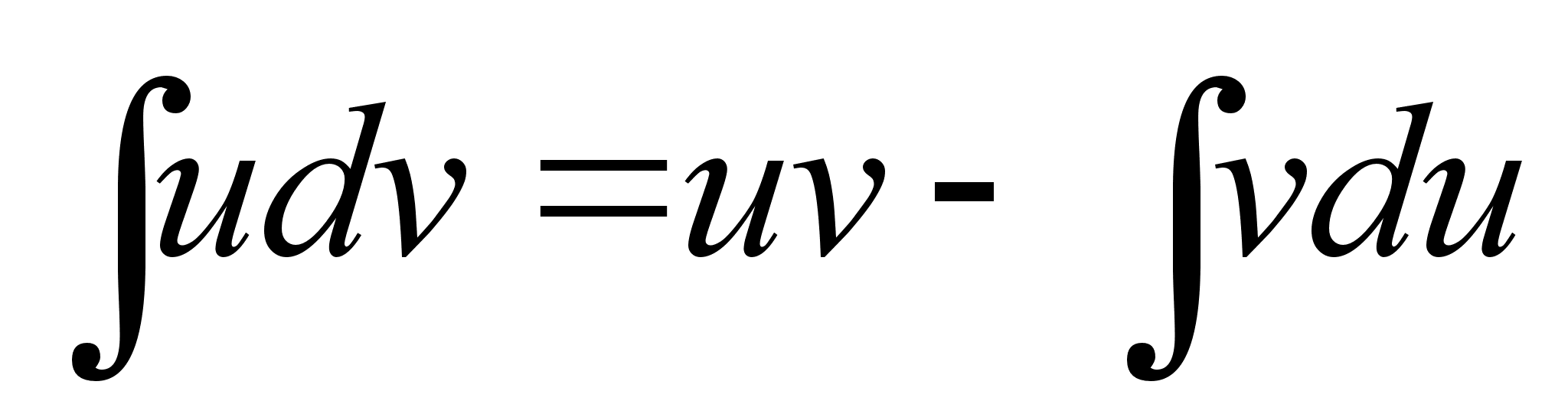 пределённого
интеграла
пределённого
интеграла
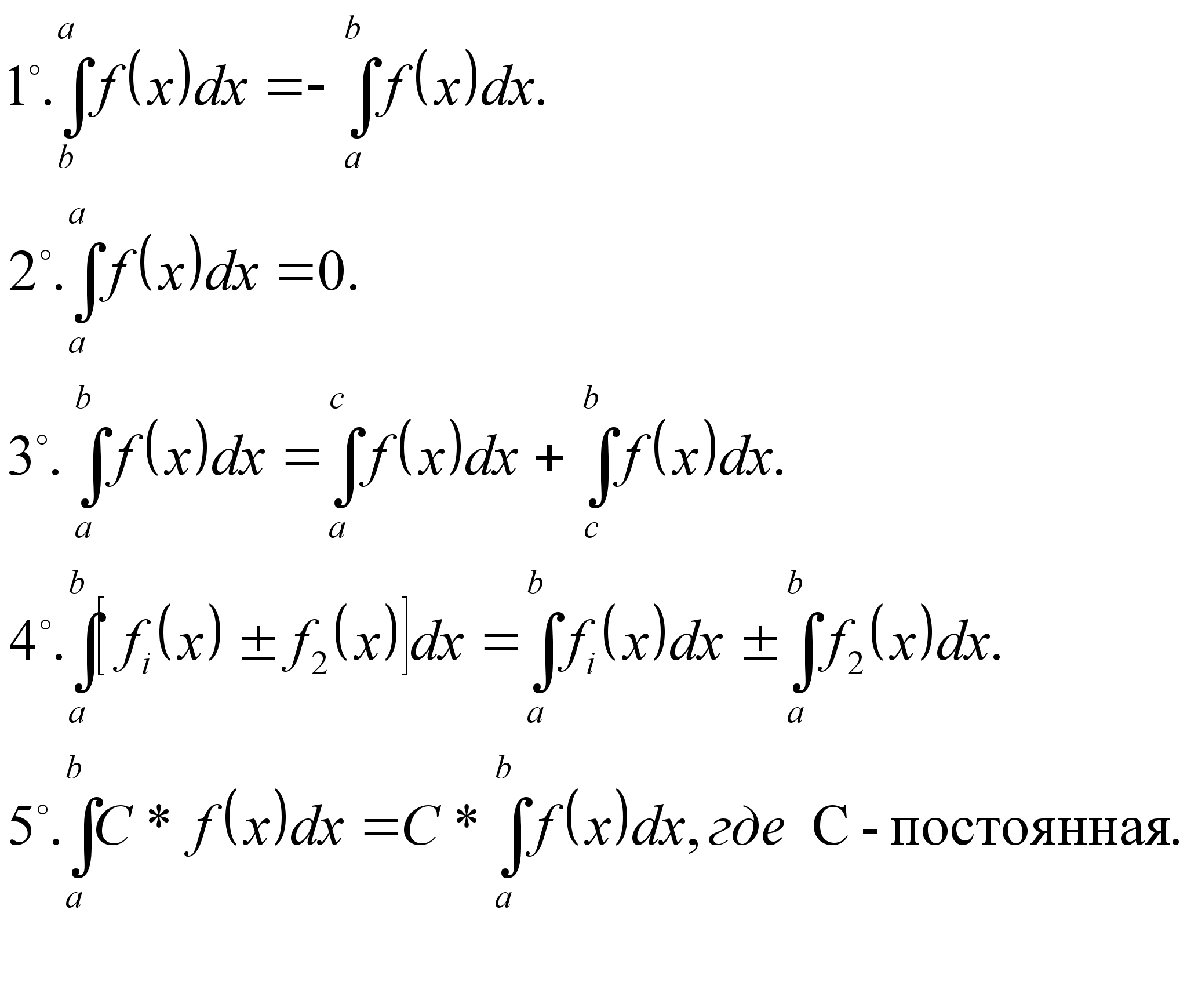
Интегрирование простейших дробей
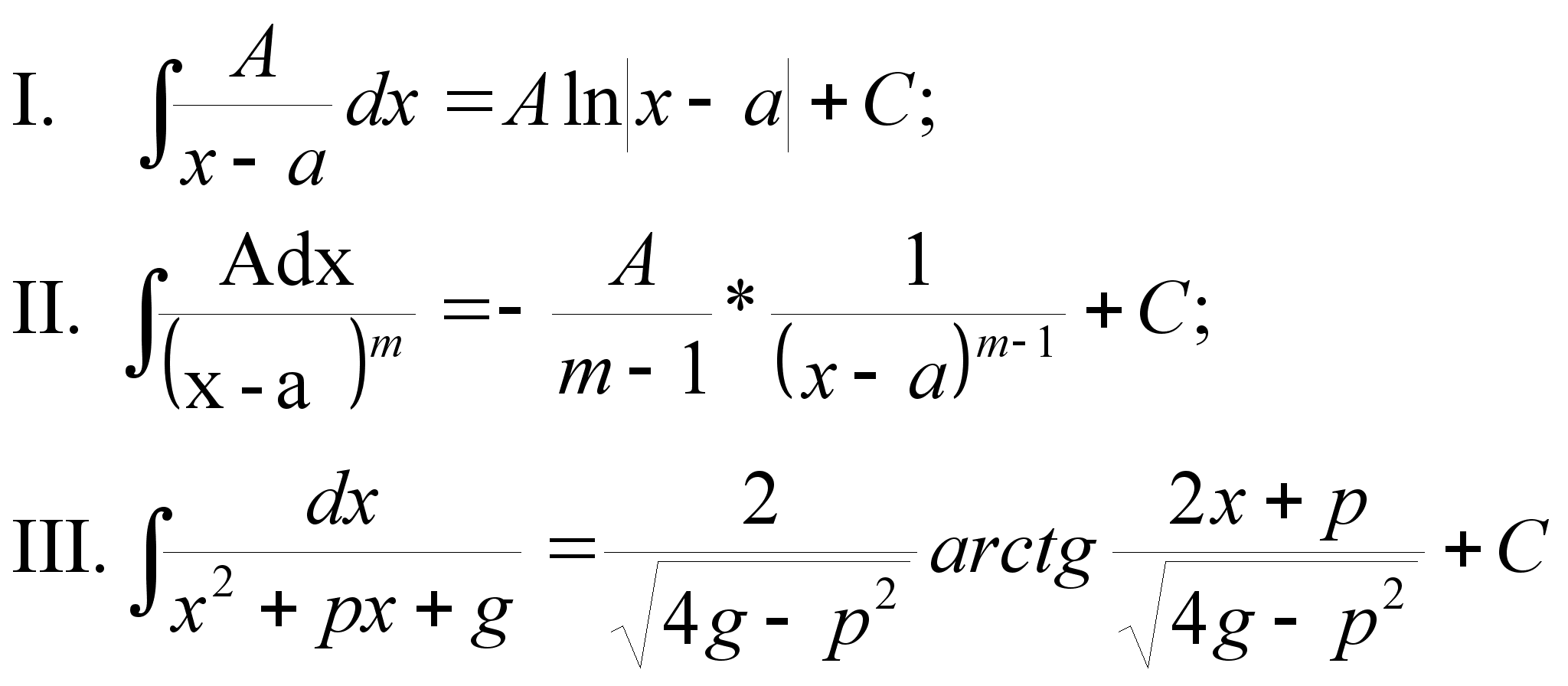
Замена переменной в
неопределенном интеграле
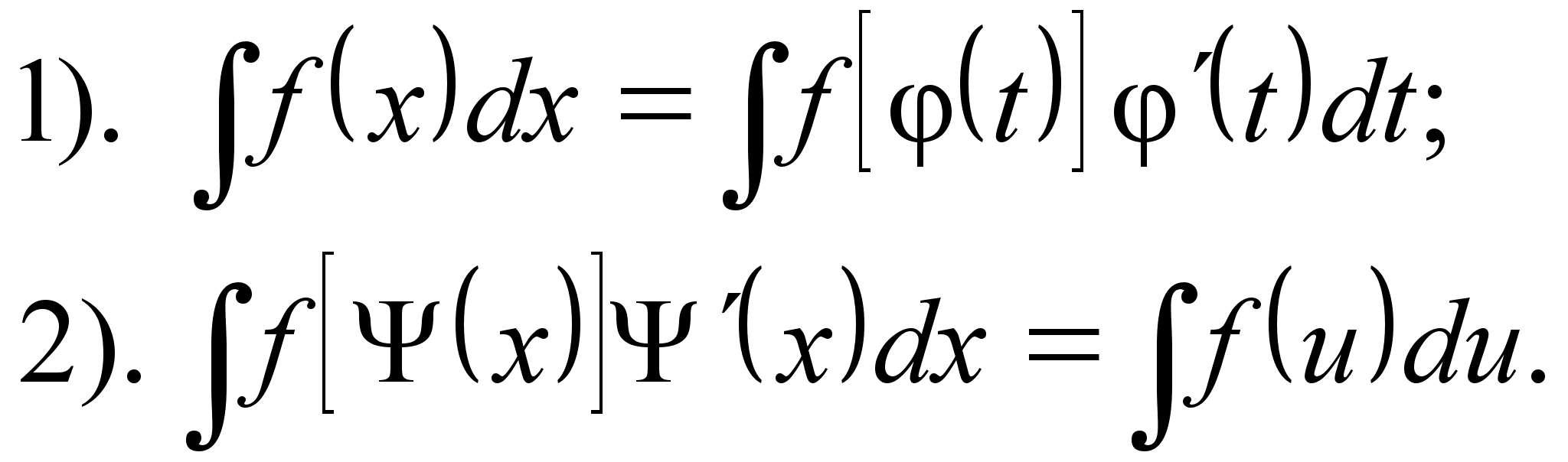

Площадь плоской фигуры
П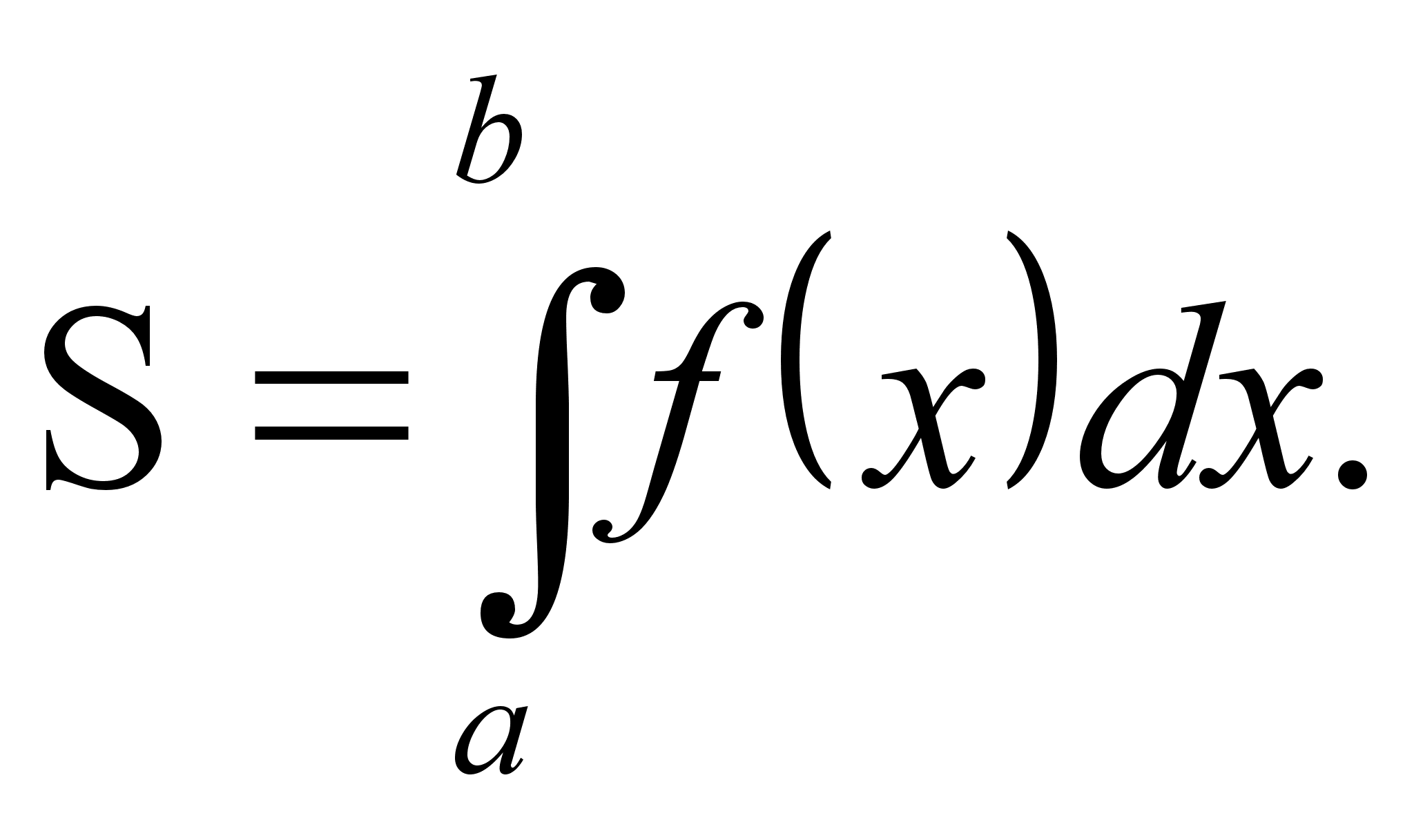 лощадь
криволинейной
трапеции,
ограниченной
кривой
лощадь
криволинейной
трапеции,
ограниченной
кривой
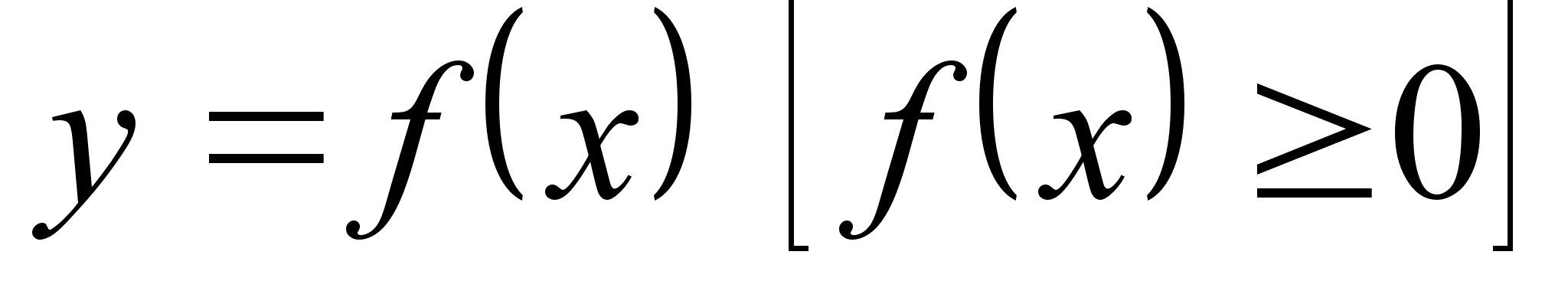 ,
прямыми
,
прямыми
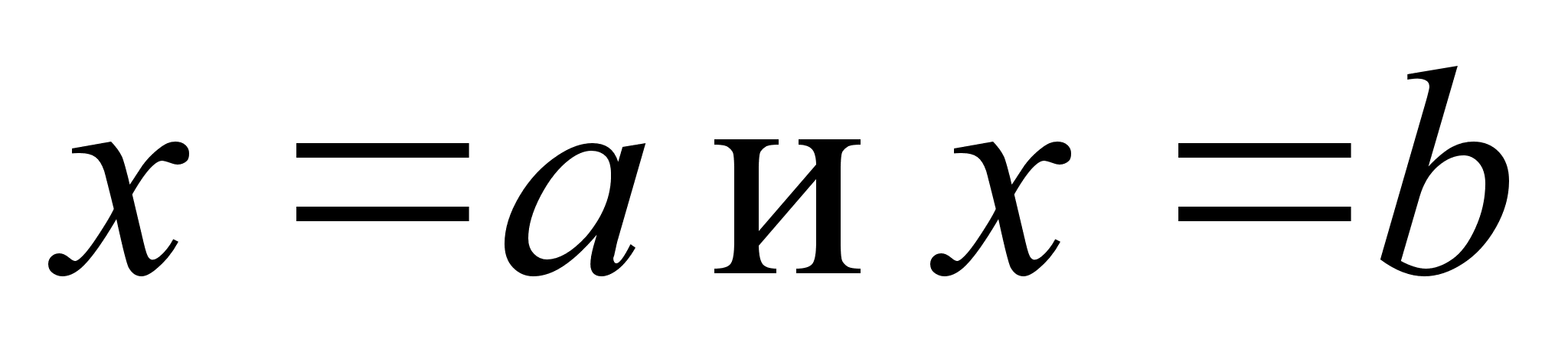 и отрезком[a,
b]
оси
Ox,
вычисляется
по формуле
и отрезком[a,
b]
оси
Ox,
вычисляется
по формуле
П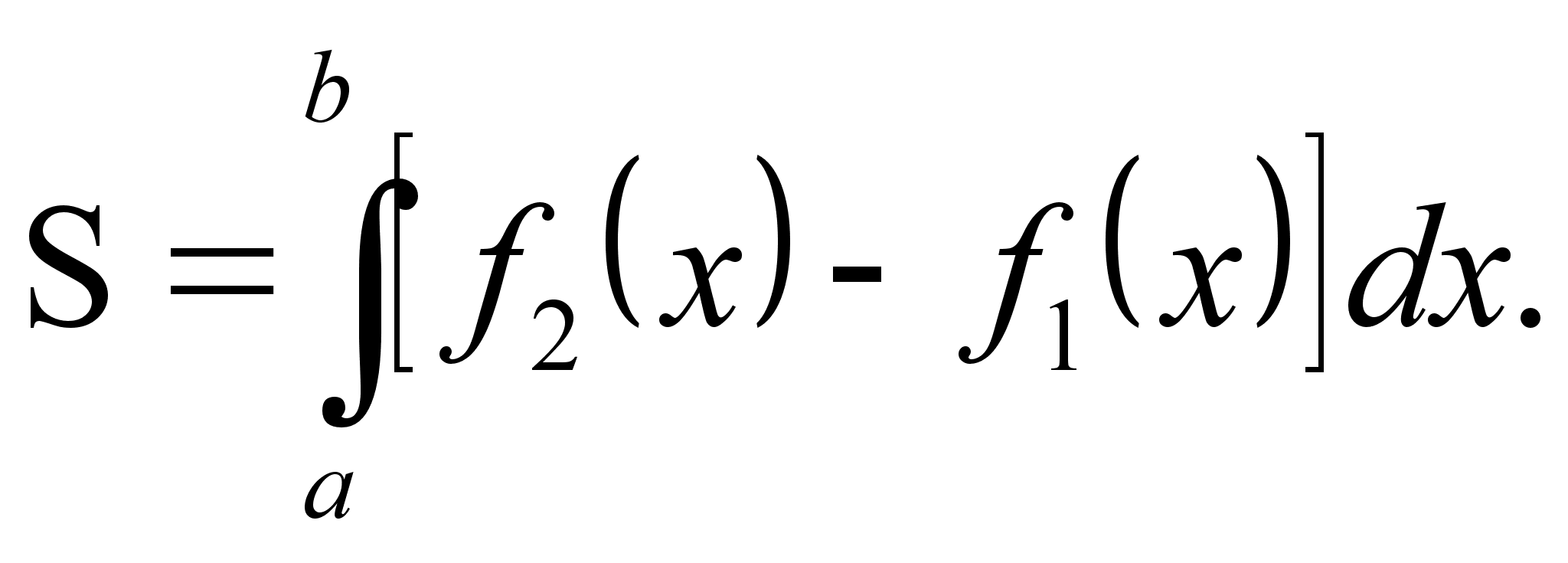 лощадь
фигуры, ограниченной
кривыми
лощадь
фигуры, ограниченной
кривыми
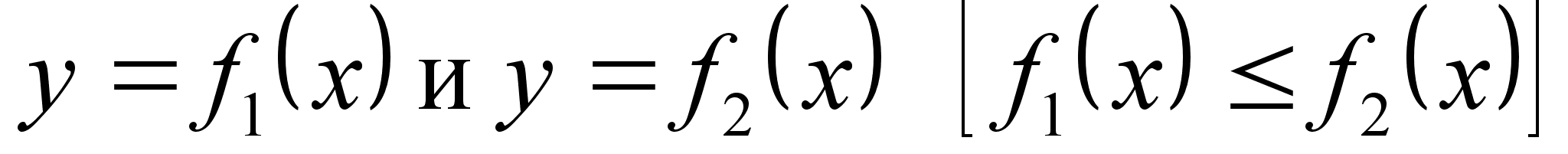 и прямыми
и прямыми
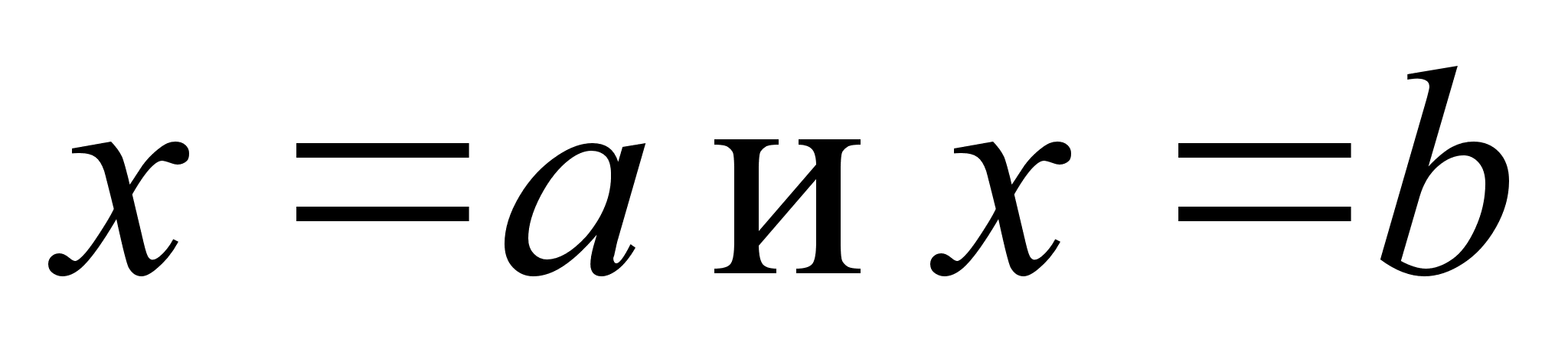 ,
находится по
формуле
,
находится по
формуле
Если
кривая задана
параметрическими
уравнениями
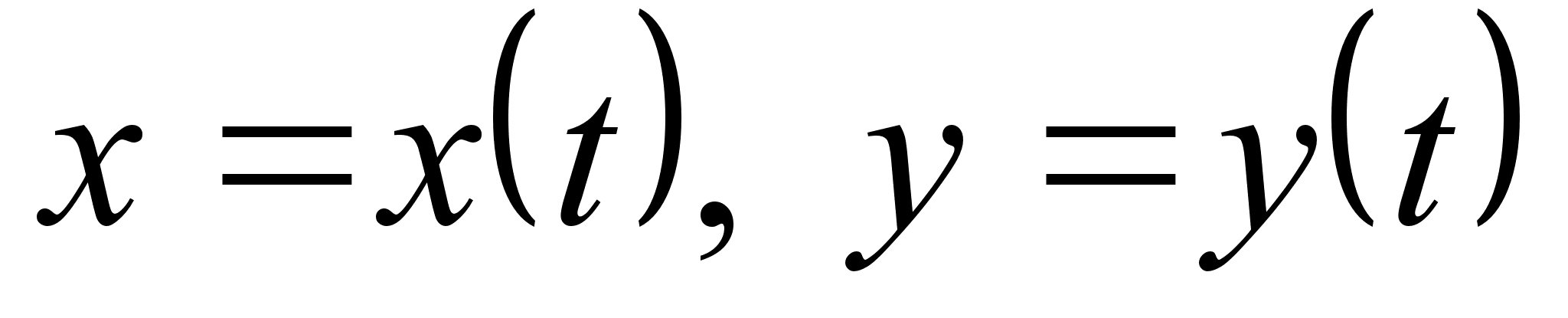 ,
то площадь
криволинейной
трапеции,
ограниченной
этой кривой,
прямыми
,
то площадь
криволинейной
трапеции,
ограниченной
этой кривой,
прямыми
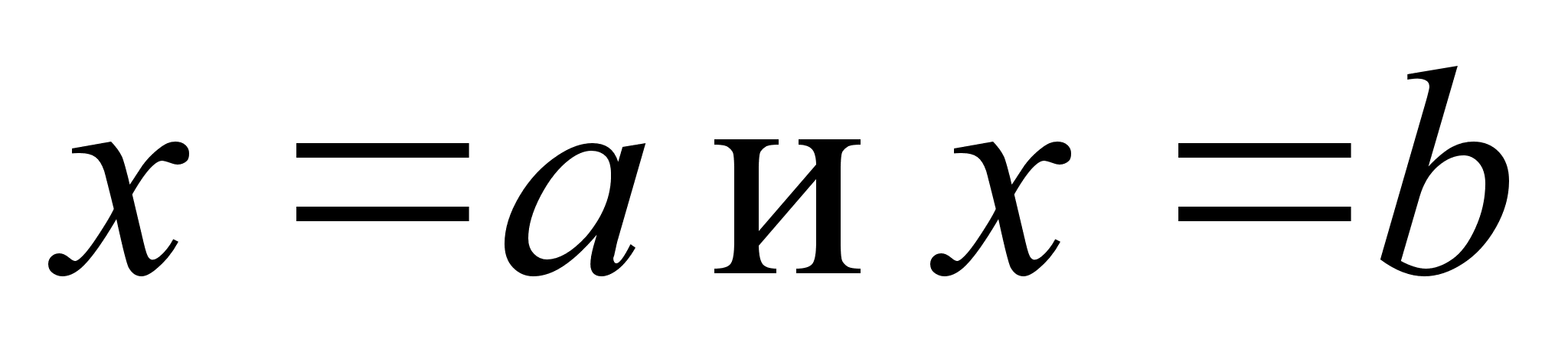 и отрезком[a,
b]
оси
Ox,
выражается
формулой
и отрезком[a,
b]
оси
Ox,
выражается
формулой
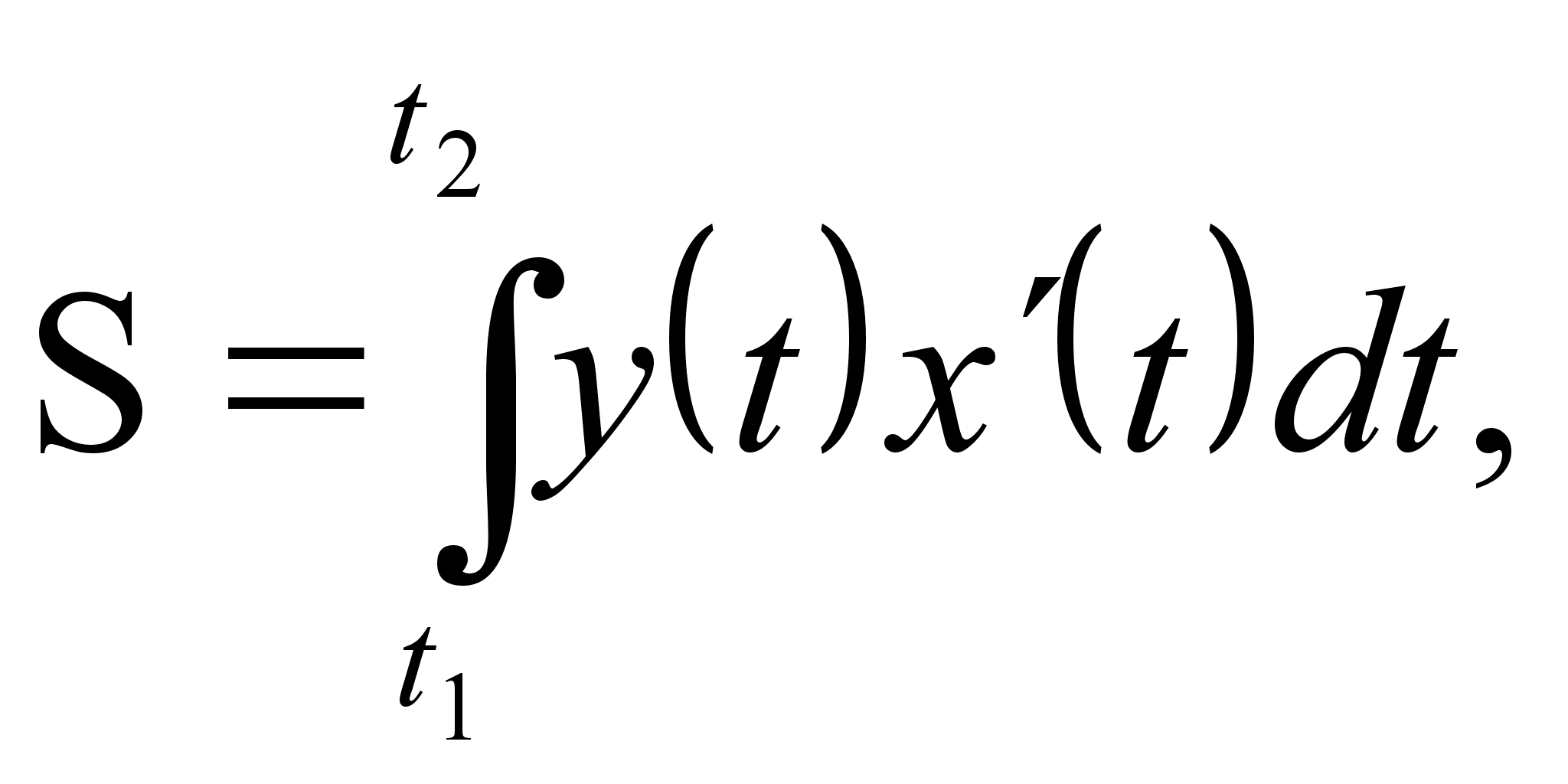
где
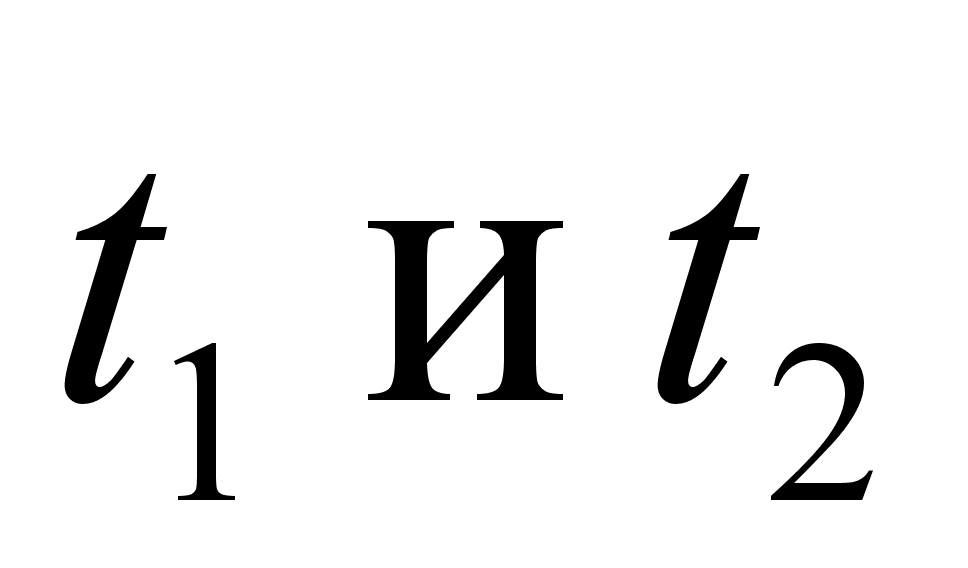 определяются
из уравнений
определяются
из уравнений
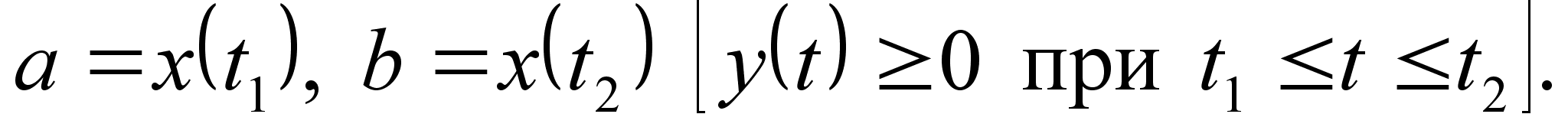
Площадь
криволинейного
сектора, ограниченного
кривой, заданной
в полярных
координатах
уравнением
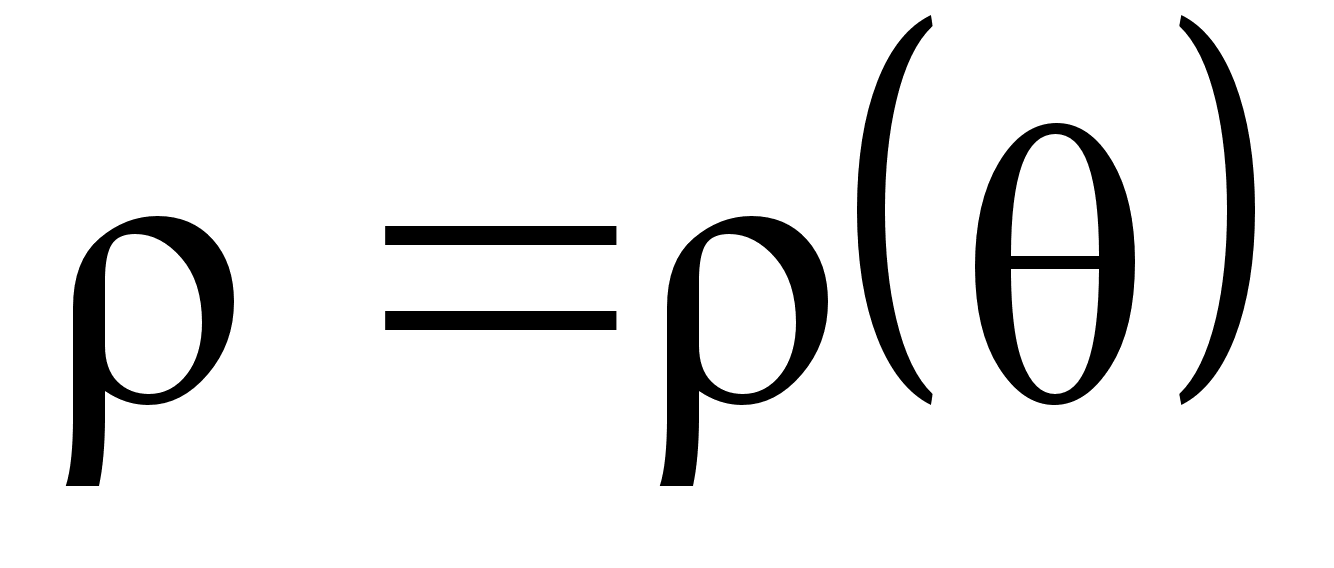 и двумя полярными
радиусами
и двумя полярными
радиусами
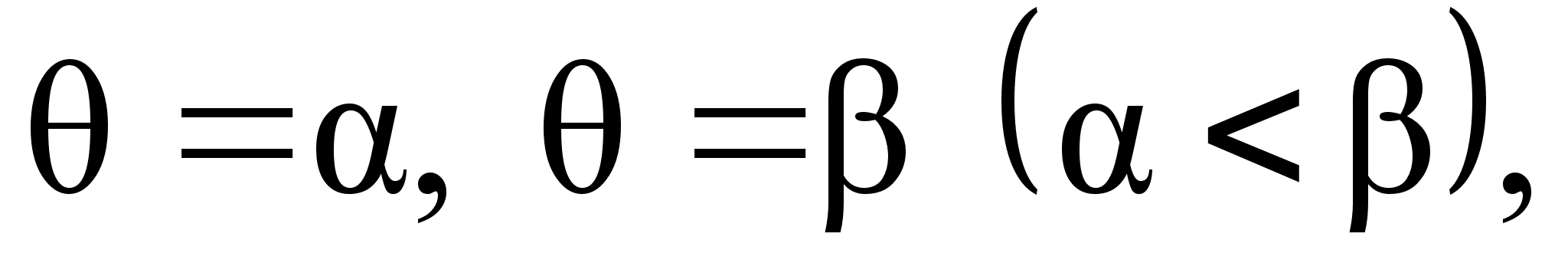 находится по
формуле
находится по
формуле
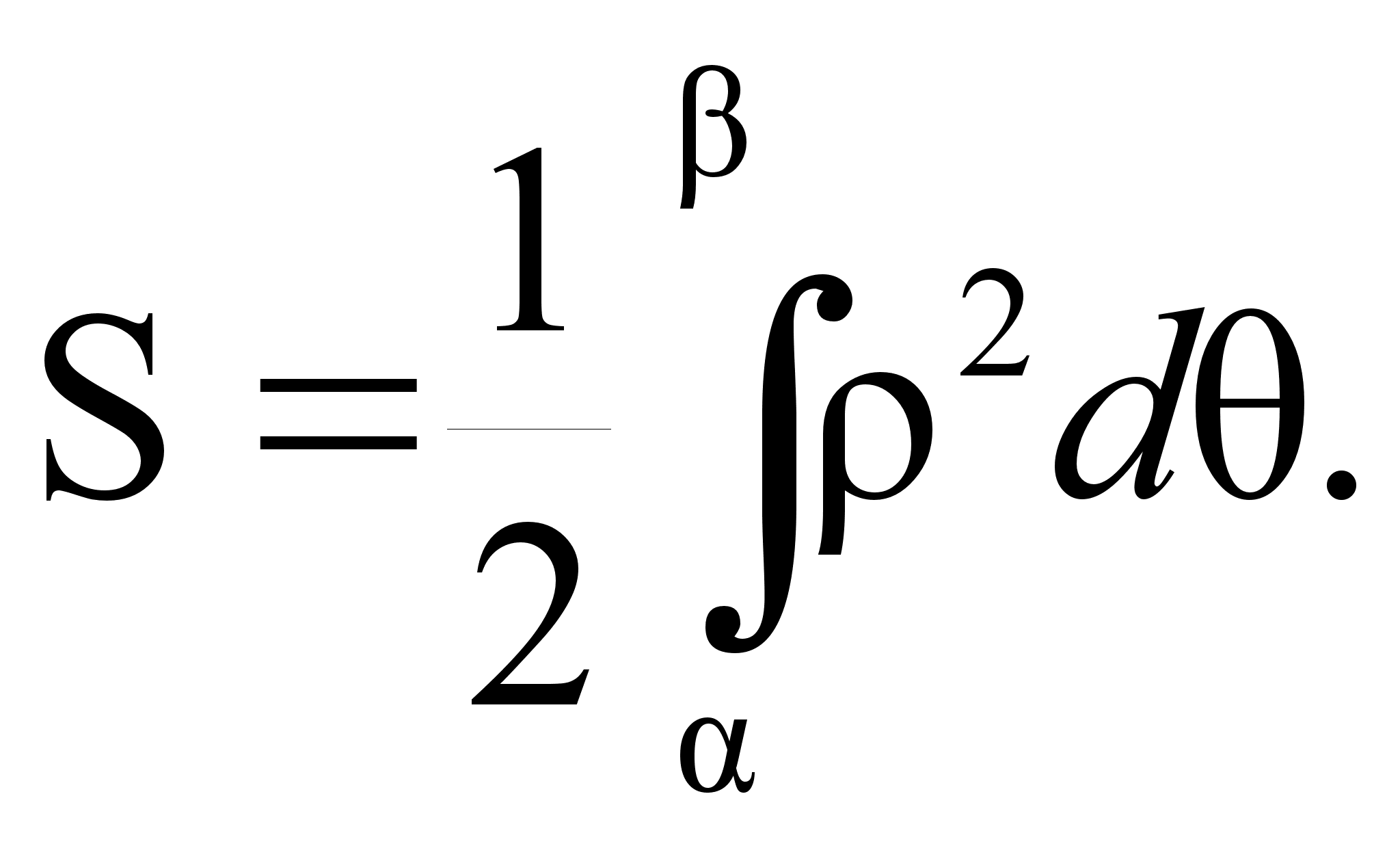
Длина дуги плоской кривой
Если
кривая y=f(x)
на
отрезке [a,
b] – гладкая
(т.е. производная
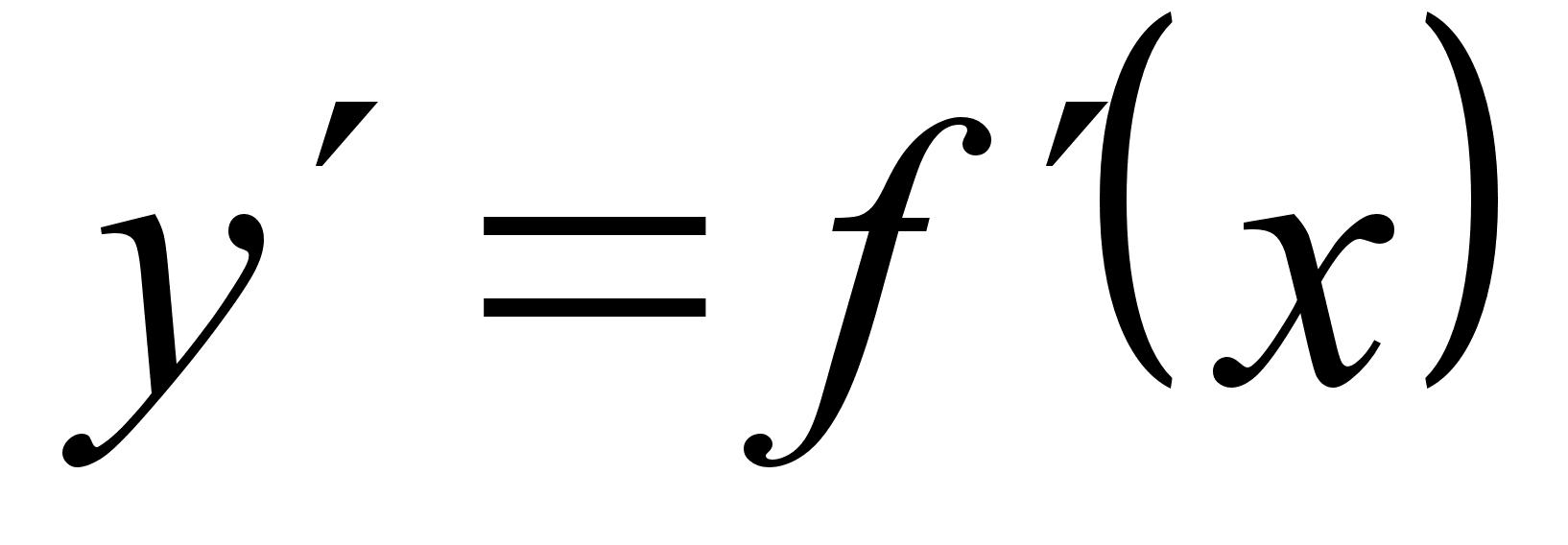 непрерывна),
то длина соответствующей
дуги этой кривой
находится по
формуле
непрерывна),
то длина соответствующей
дуги этой кривой
находится по
формуле
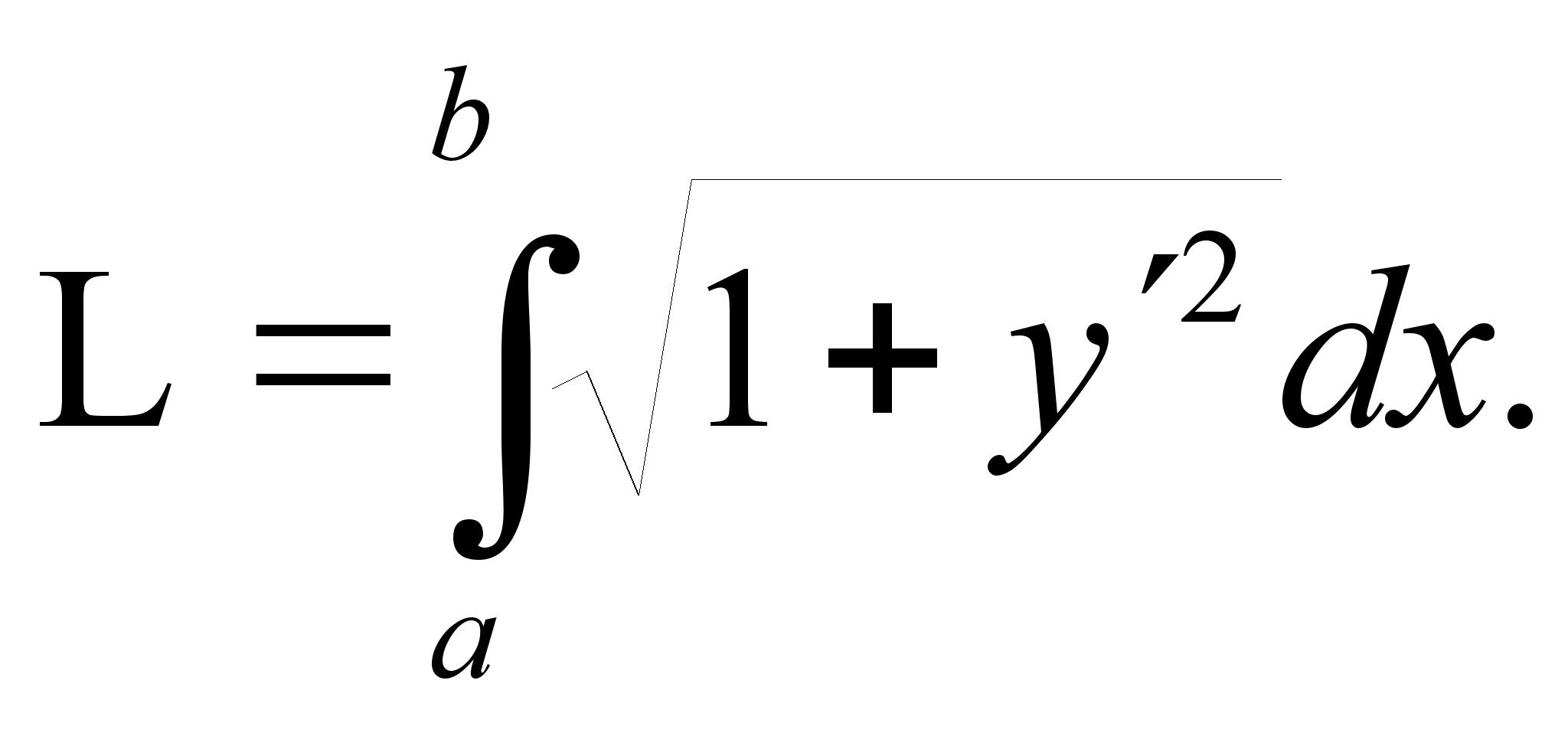
При
параметрическом
задании кривой
x=x(t),
y=y(t) [x(t) и
y(t) – непрерывно
дифференцируемые
функции]
длина
дуги кривой,
соответствующая
монотонному
изменению
параметра
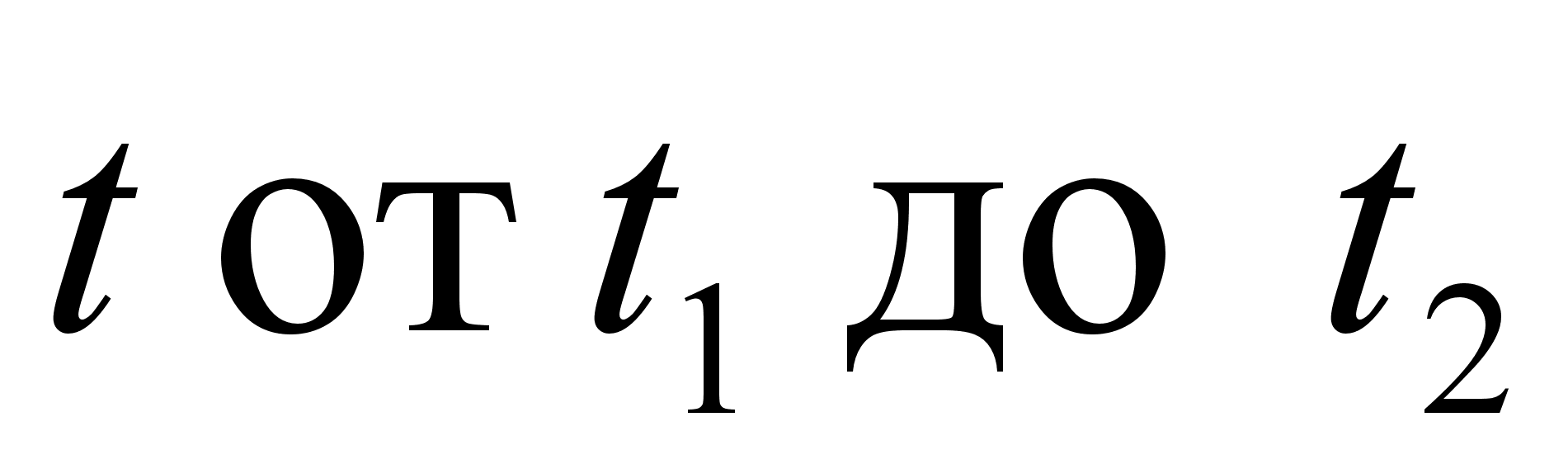 ,
вычисляется
по формуле
,
вычисляется
по формуле
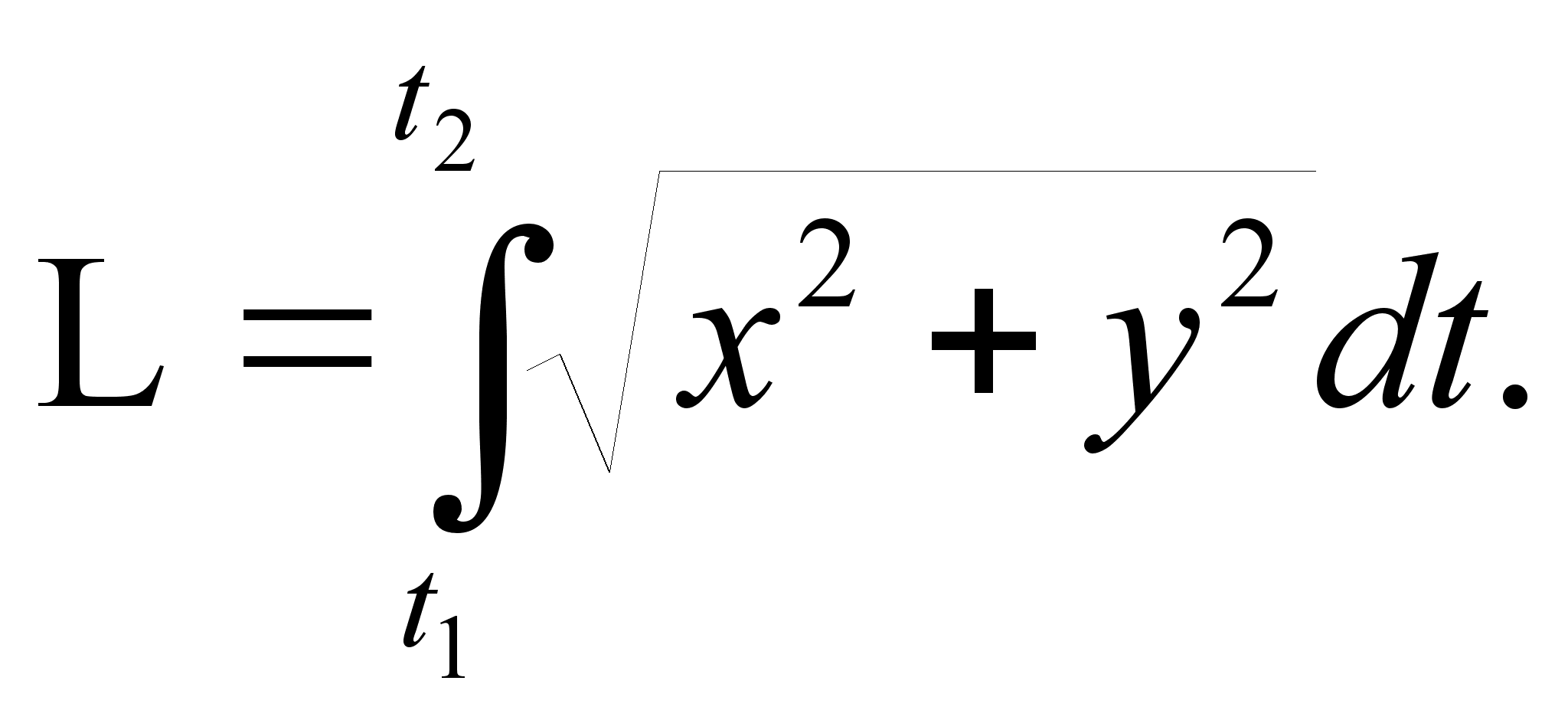
Е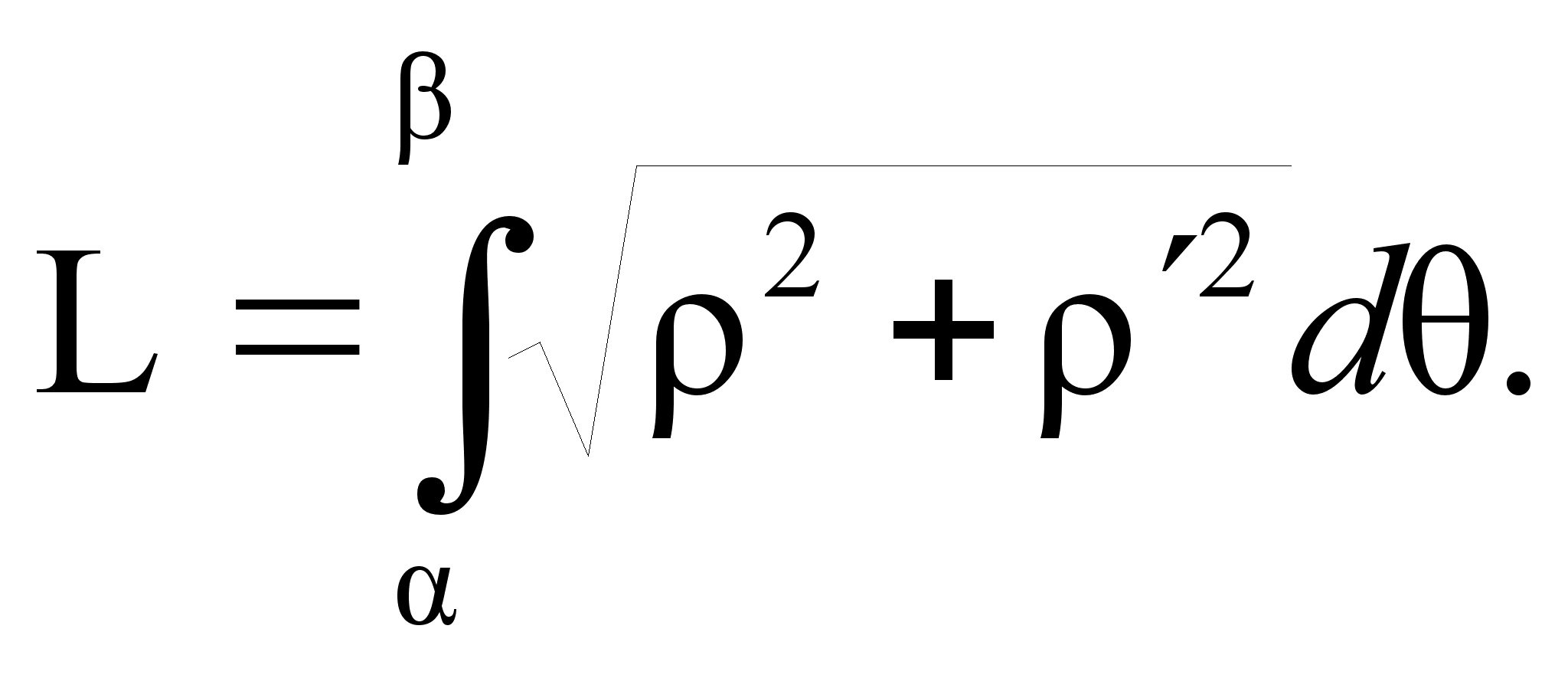 сли
гладкая кривая
задана в полярных
координатах
уравнением
сли
гладкая кривая
задана в полярных
координатах
уравнением
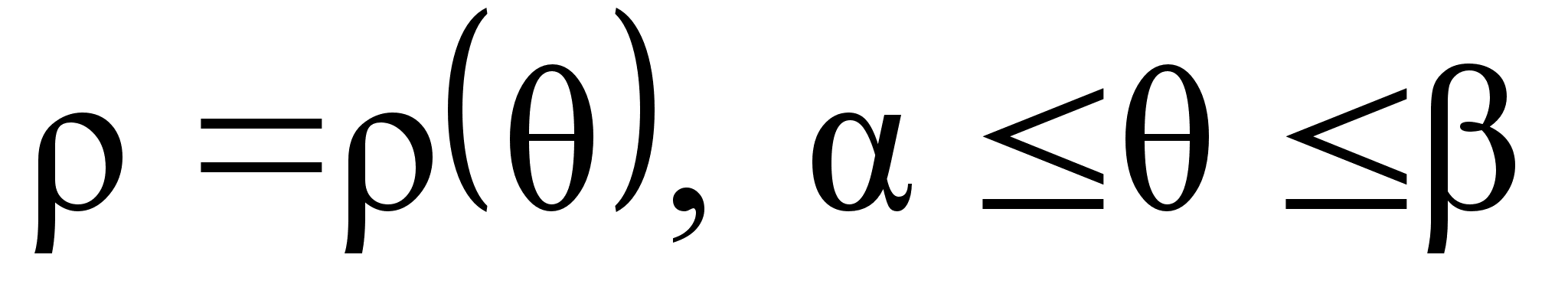 ,
то длина дуги
равна
,
то длина дуги
равна
Вычисление объема тела
Вычисление объема тела по известным площадям поперечных сечений.
Е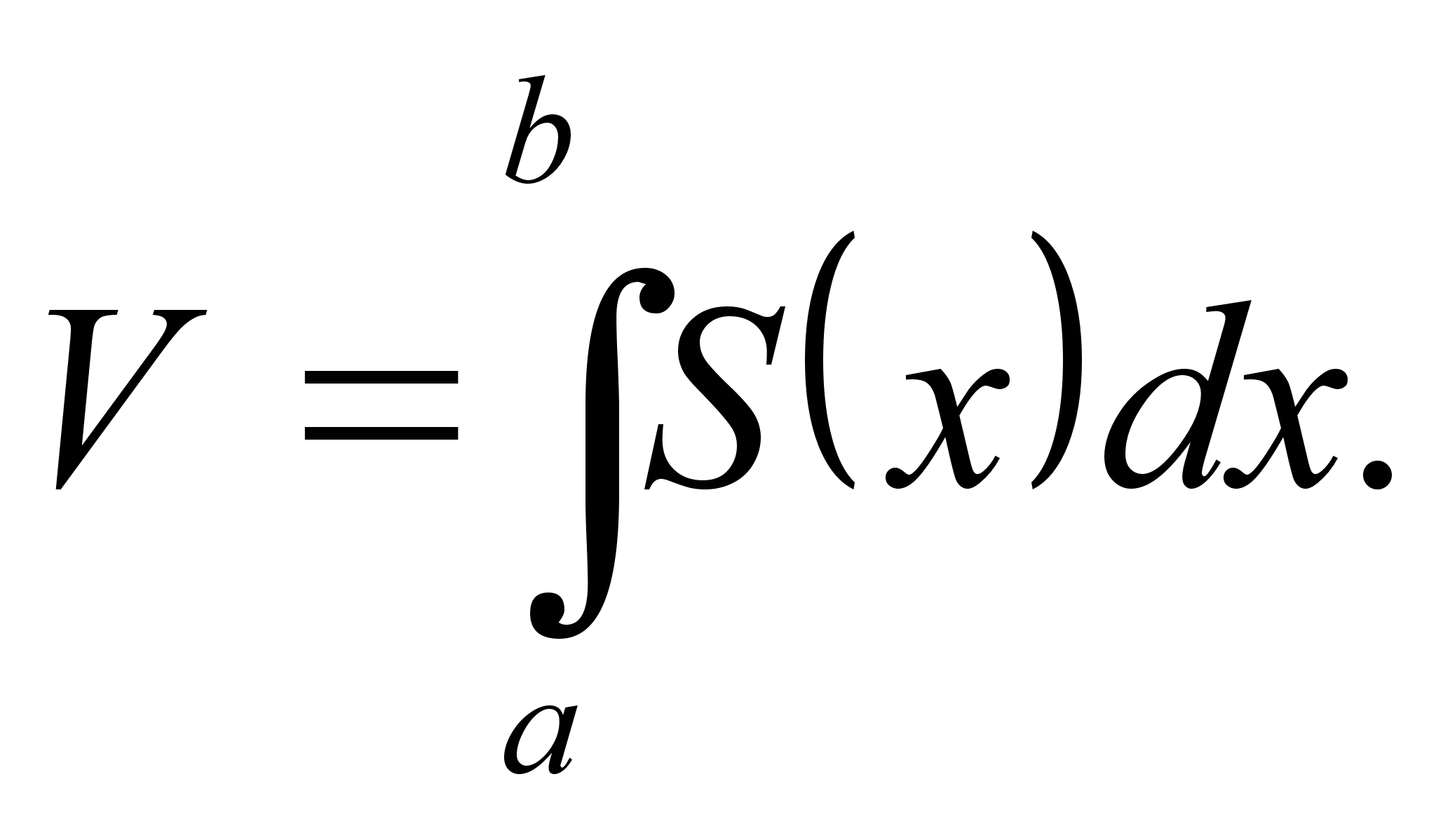 сли
площадь сечения
тела плоскостью,
перпендикулярной
оси Ox,
может
быть
выражена как
функция от x,
т.е. в виде
сли
площадь сечения
тела плоскостью,
перпендикулярной
оси Ox,
может
быть
выражена как
функция от x,
т.е. в виде
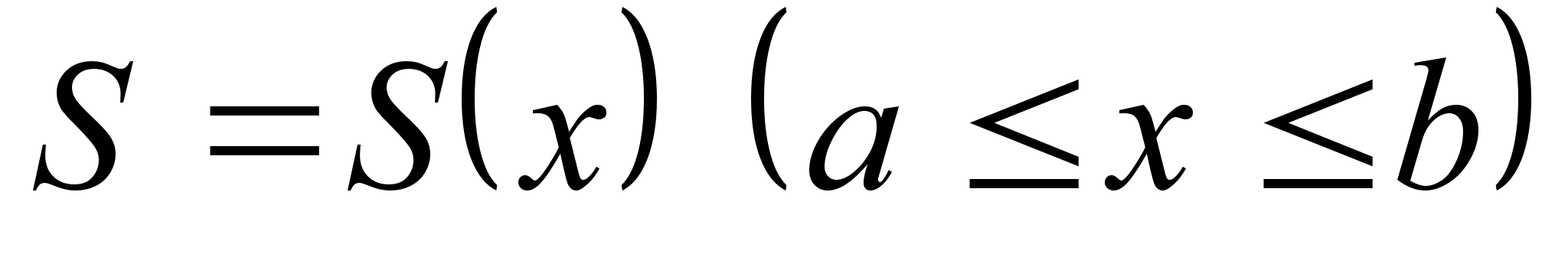 ,
то объем части
тела, заключенной
между перпендикулярными
оси Ox
плоскостями
x=a
и
x=b,
находится по
формуле
,
то объем части
тела, заключенной
между перпендикулярными
оси Ox
плоскостями
x=a
и
x=b,
находится по
формуле
Вычисление объема тела вращения. Если криволинейная трапеция, ограниченная кривой
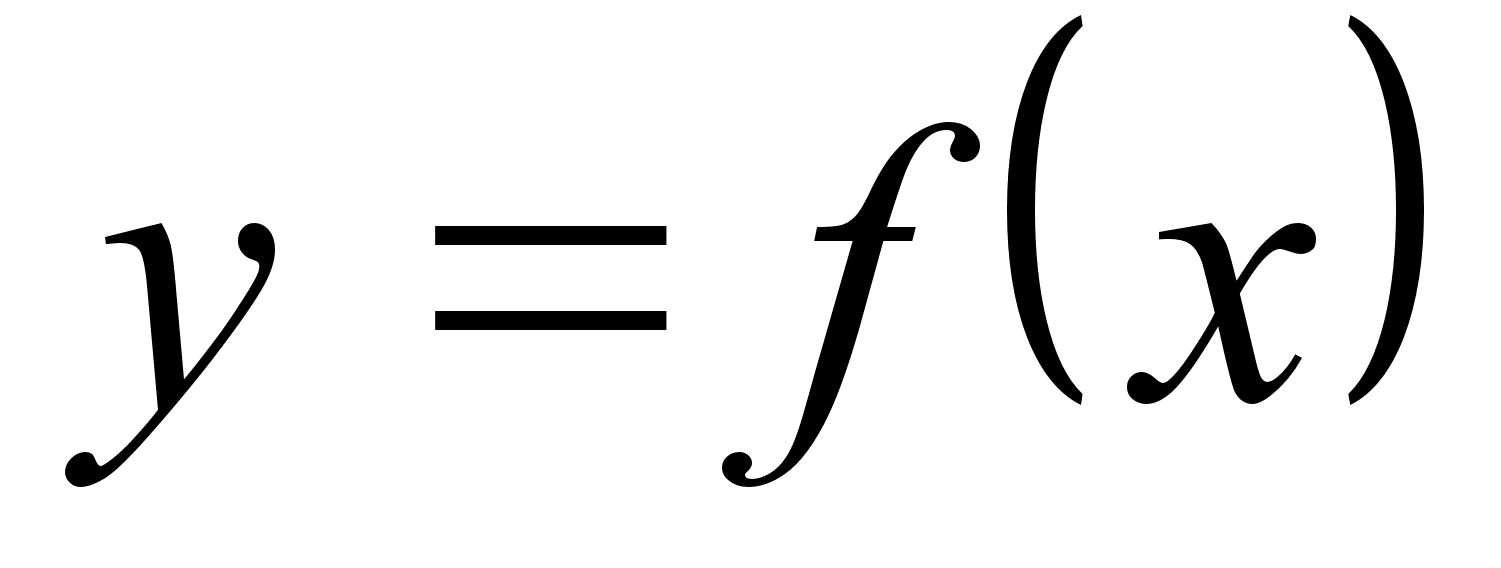 и прямыми
и прямыми
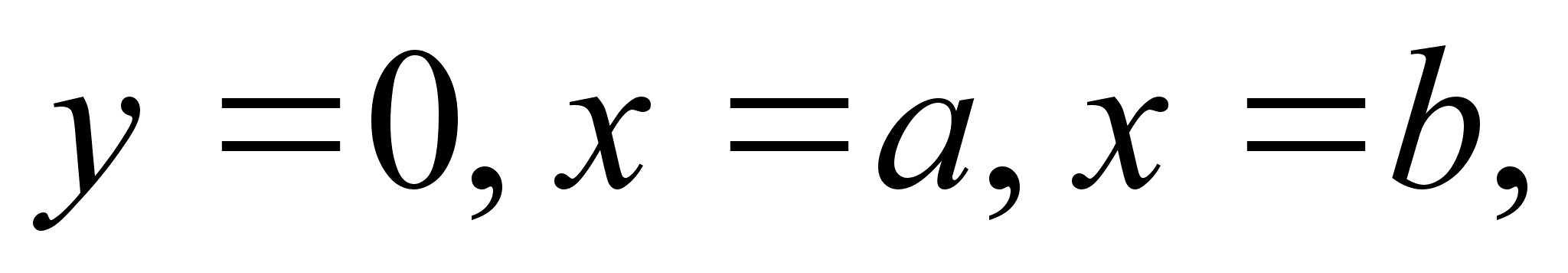 вращается
вокруг оси Ox,
то объем тела
вращения вычисляется
по формуле
вращается
вокруг оси Ox,
то объем тела
вращения вычисляется
по формуле
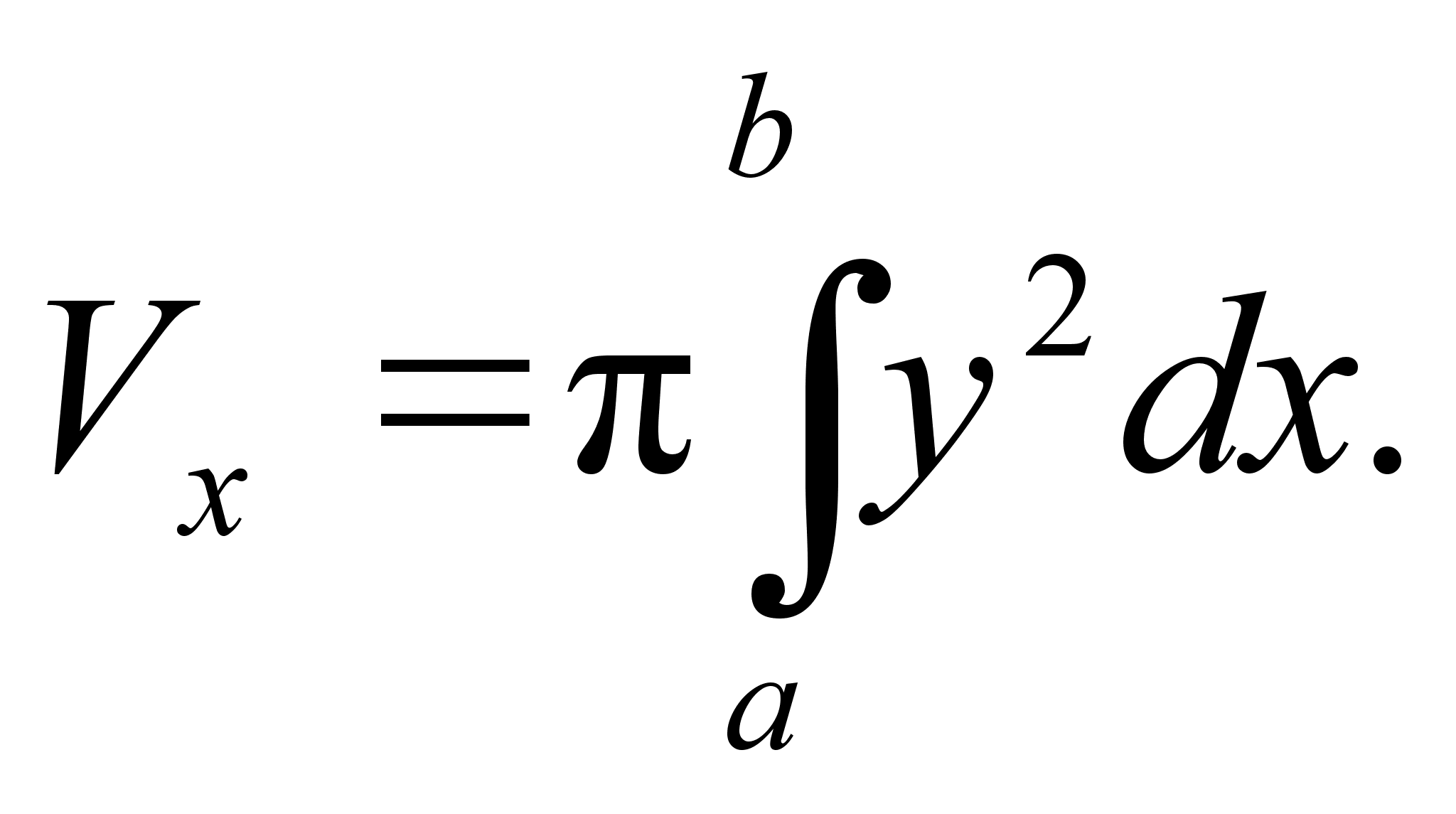
Е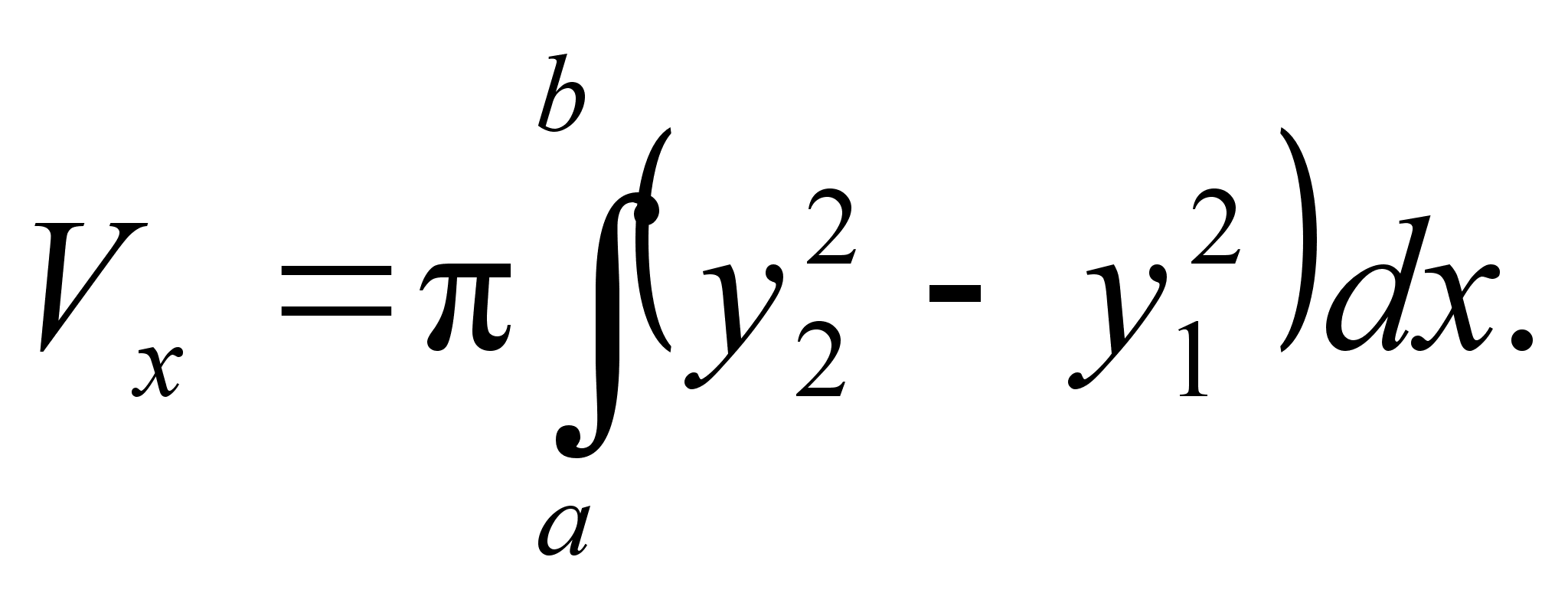 сли
фигура, ограниченная
кривыми
сли
фигура, ограниченная
кривыми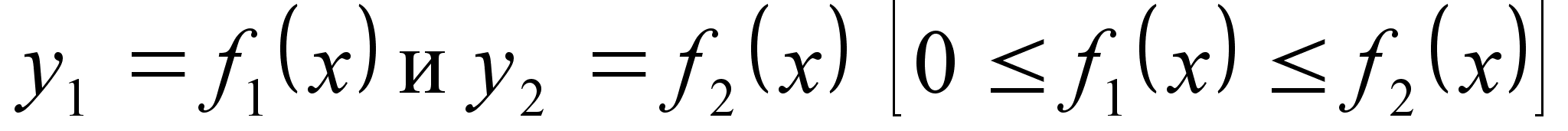 и прямыми x=a,
x=b,
вращается
вокруг оси Ox,
то объем тела
вращения
и прямыми x=a,
x=b,
вращается
вокруг оси Ox,
то объем тела
вращения
Вычисление площади поверхности вращения
Е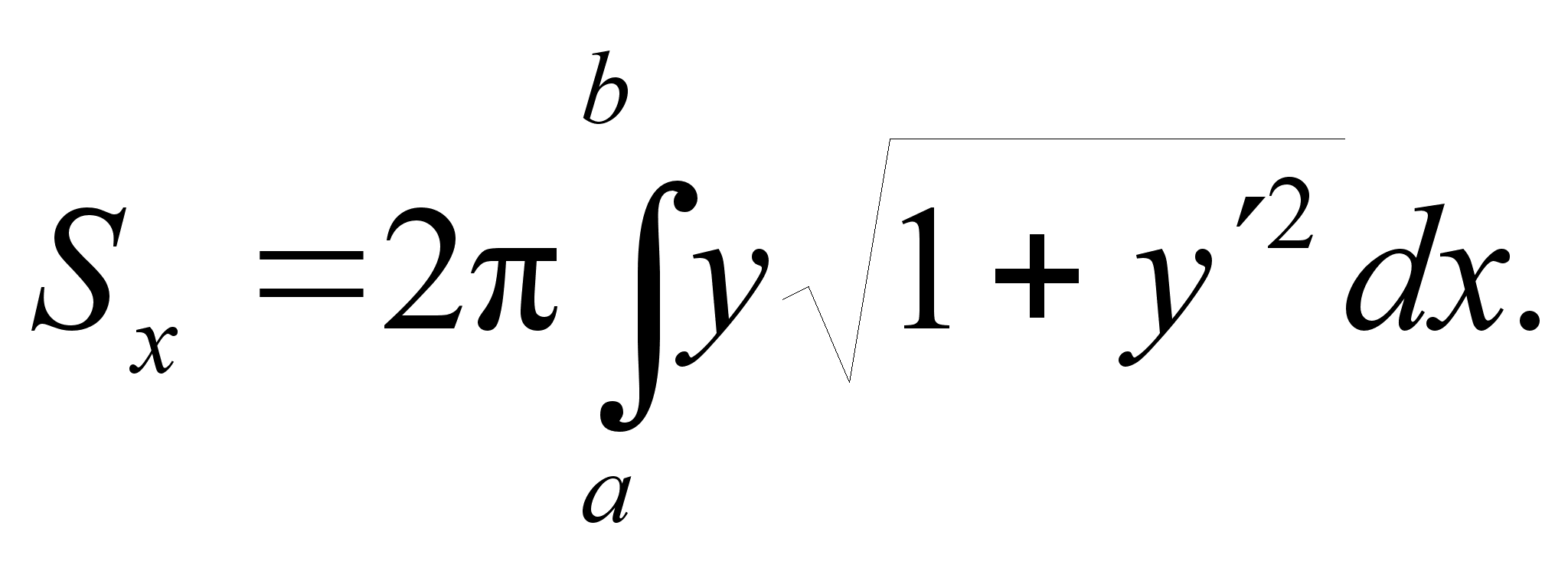 сли
дуга гладкой
кривой
сли
дуга гладкой
кривой
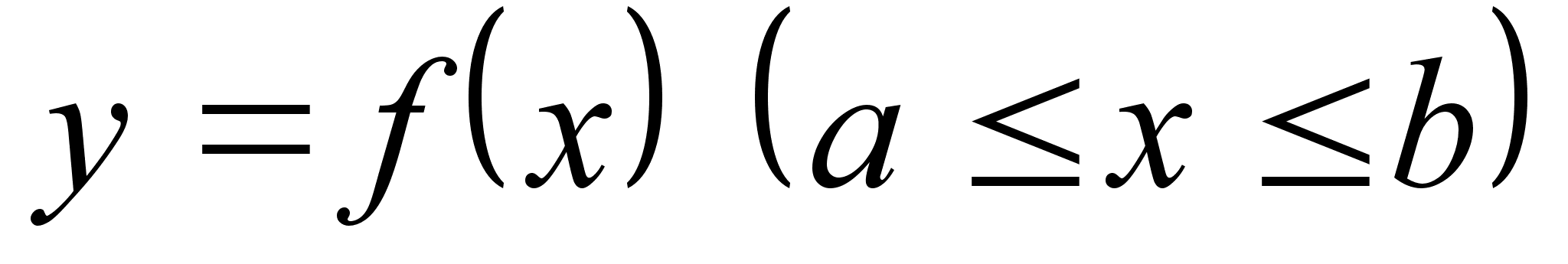 вращается
вокруг оси
Ox,
то площадь
поверхности
вращения вычисляется
по формуле
вращается
вокруг оси
Ox,
то площадь
поверхности
вращения вычисляется
по формуле
Е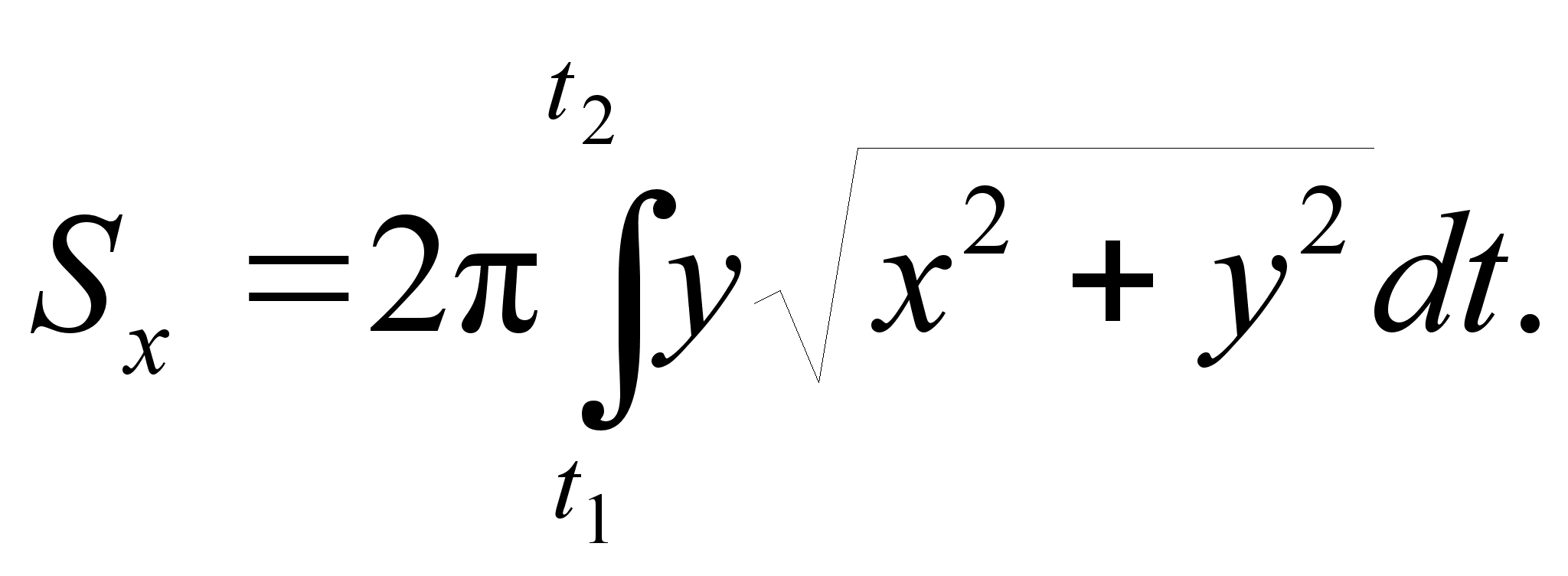 сли
кривая задана
параметрическими
уравнениями
сли
кривая задана
параметрическими
уравнениями
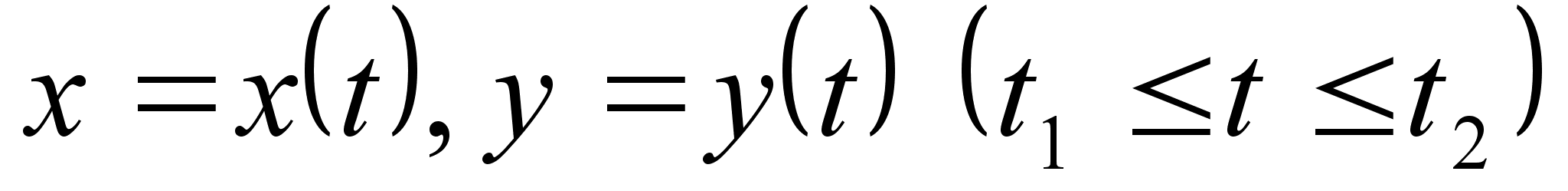 ,
то
,
то
