Логарифмічно-лінійний аналіз

КОНТРОЛЬНА РОБОТА

ЛОГАРИФМІЧНО ЛІНІЙНИЙ АНАЛІЗ

Зміст

1. Основні поняття логлінійного аналізу

2. Аналіз зв’язку категоризованих змінних

3. Канонічна кореляція при аналізі таблиць спряженості ознак

4. Побудова логарифмічної моделі

Висновки

Список використаних джерел

Основні поняття логлінійного аналіза

Останніми роками активно розробляються методи аналізу таблиць спряженості ознак. Це пояснюється в першу чергу наявністю некількісних (так званих якісних) величин в описі соціально-економічних об'єктів, потребами вивчення зв'язків між ними. Таблиця спряженості є універсальною формою подання даних, яка не пов'язана з рівнем вимірювання ознак. Будь-яку величину можна представити як категоризовану.

В медичних дослідженнях частіше реєструються величини, які оцінюються якісно. Тоді при спостереженні n об'єктів, кожні з k ознак, що описують ці об'єкти, подаються у вихідній матриці кодами їх категорій (рівнів). За даною вихідною матрицею спостережень одержують таблицю спряженості, яка включає частоти спостережень при всіх комбінаціях рівнів ознак.

Одним з основних питань, яке виникає при обробці даних, є питання про наявність взаємозв'язку між ознаками. Методом багатовимірного статистичного аналізу, який використовується для обробки багатовимірних таблиць спряженості, є логлінійний аналіз.

Основна ідея логлінійного аналізу полягає в тому, що в кожній комірці таблиці спряженості записується розклад натурального логарифма частоти на суму ефектів всіх взаємозв'язків досліджуваних ознак. Модель к-го порядку називається насиченою, якщо вона крім головних ефектів містить будь-які взаємозв'язки величин від другого до к-го порядків включно. Так, наприклад, для 3-х факторів A, B, C насичена модель має вигляд:

(1.1)

де μ - загальне середнє,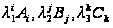 - головні ефекти досліджуваних ознак. Так, наприклад, 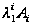можна інтерпретувати як додаток (спад, якщо її знак від’ємний) i-ой категорії фактора A в порівнянні із загальним середнім, що є мірою того, наскільки ймовірна i-а категорія ознаки А в порівнянні з іншими; 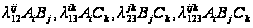- ефекти відповідних взаємодій. Насичена модель містить стільки ж параметрів, скільки і комірок в таблиці спряженості. Для того, щоб модель була не надлишковою, тобто, щоб число параметрів не перевищило число елементів () досліджуваної таблиці спряженості, на значення в моделі накладаються наступні обмеження:

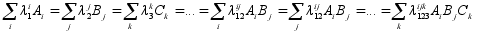
(1.2)

Сенс дослідження полягає в тому, щоб знайти найбільш економне пояснення даних, представлених в таблиці спряженості (найбільш просту структуру). Окрім насичених моделей часто використовують ієрархічні моделі, які отримують з насичених шляхом послідовного виключення ефектів, що не є значущими. При ієрархічній побудові включення в модель взаємодій к-го порядку вимагає включення всіх взаємодій нижчого порядку, а також всіх головних ефектів. Як і в регресійному аналізі для виключення неістотних дій можуть застосовуватися методи покрокового включення і покрокового виключення змінних. В результаті видалення неістотних ефектів можуть мати місце наступні види моделей:

1) 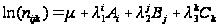- такі моделі називаються моделями незалежності. Вони містять лише головні ефекти, відсутні ефекти взаємодії чинників.

2) - категорії факторів В і С – рівноймовірні.

3) 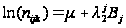- категорії факторів А і С – рівноймовірні.

4) 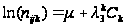- категорії факторів В і А – рівноймовірні.

5) 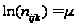- всі категорії всіх факторів – рівноймовірні.

6) 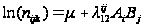- має місце взаємозв'язок двох ознак А і В. Така модель не відноситься до ієрархічних.

7) - має місце взаємозв'язок двох ознак В і С.

2. Аналіз зв’язку категоризованих змінних

Дуже часто вивчення взаємозв'язків між якісними змінними зводитися до аналізу двох змінних х і у, які набувають низку значень – х1, …, хm і y1,…, yp. Позначимо номер рядка двовимірної таблиці через і (і = 1,…, m), номер стовпця – через j (j = 1,…,р). Кожен об'єкт характеризується значеннями двох змінних хi і yj. У комірках таблиці записується число об'єктів у вибірці, що володіють даним поєднанням значень ознак (коміркова частота) – nij.

Як правило, аналіз двовимірних таблиць спряженості обмежується висновками про наявність зв'язку і її тісноти. Класичним тестом, який використовується для встановлення факту наявності зв'язку, є критерій χ2. Величина χ2 звичайно визначається як сума квадратів між фактичними (nij) і теоретичними (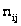) частотами двовимірного розподілу, поділена на теоретичні частоти.

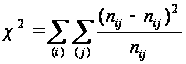(2.1)

Нульовою гіпотезою є: 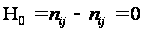. Розрахунок очікуваних частот двовимірного розподілу проводиться в припущенні про статистичну незалежність змінних

(2.2)

де 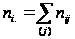- сума за і-тим рядком таблиці, 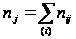- сума за j-м стовпцем таблиці (так звані маргінальні частоти). Обираючи рівень значущості λ, визначають відповідне критичне значення критерію χ2λ;df при числі ступенів вільності df = (m - 1)(p - 1). Якщо розрахункова величина χ2 перевищує критичне значення χ2λ;df, то на даному рівні значущості нульова гіпотеза Н0 може бути відхилена.

Аналіз якісних змінних передбачає використання багатовимірних методів. Існуючі взаємозв'язки між змінними вимагають їх спільного розгляду, переходу від парних зв'язків до аналізу множинних і частинних зв'язків, від двовимірних таблиць спряженості до складних комбінаційних таблиць. Ця потреба добре усвідомлюється дослідниками, але проте часто не реалізується.

Розглянемо ряд методів аналізу зв'язків якісних змінних і виявлення структури вихідних даних в багатовимірних комбінаційних таблицях. Перш за все зупинимося на простому прийомі аналізу, заснованому на розкладанні критерію χ2. Звичайно й оцінка значущості зв'язку, і вимірювання її інтенсивності проводитися за таблицею в цілому.

При цьому не виявляється дуже важлива інформація про зміну інтенсивності зв'язку змінних із зміною їх значень: при одних значеннях зв'язок ознак може бути щільним, при інших – слабким і навіть взагалі не спостерігатися. Узагальнюючи різний ступінь інтенсивності зв'язку в єдиному показнику, ми можемо дійти парадоксальних висновків, загубити практично значущі випадки. Щоб уникнути цього, корисно аналізувати окремі фрагменти початкової таблиці. Перехід від таблиці в цілому до окремих її частин доцільний як у разі багатовимірного аналізу, так і за наявності великого числа категорій двовимірного розподілу. На виділення частинних зв'язків заснована ціла низка статистичних методів, наприклад дисперсійний аналіз, логлінійний аналіз.

Використання розкладання статистики χ2 припускає перетворення вихідної таблиці спряженості в безліч таблиць розмірністю 2Ч2, кожна з яких характеризує особливий аспект зв'язку, що вивчається, – зв'язок між певними значеннями змінних. Число таких таблиць повинне дорівнювати числу ступенів вільності критерію χ2, при його обчисленні за вихідною таблицею. Кожний з локальних зв'язків у виділеному фрагменті загальної таблиці оцінюється за допомогою критерію χ2, що має одну степінь вільності. Зв'язок загальної величини статистики χ2 із значеннями, знайденими по виділених частинах таблиці, виражається рівністю:

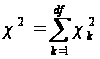(2.3)

де χk2 – k –та компонента загальної величини χ2, знайдена за загальною таблицею 2х2.

Рівність (2.3) справедлива при означенні оцінки χ2 методом максимальної правдоподібності (χML2), яка має вигляд:

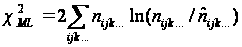(2.4)

Зазвичай вираз (2.4), знайдений відповідно до загального методу найменших квадратів, не має властивості адитивності: в цьому випадку сума окремих χk2 не обов'язково буде точно дорівнювати загальному χ2 для всієї таблиці. Відмітимо, що властивість адитивності χML2 використовується в одному з сучасних методів багатовимірного аналізу якісних змінних – логлінійному аналізі.

3. Канонічна кореляція в аналізі таблиць спряженості

Один з напрямів аналізу таблиці спряженості пов'язаний з «оцифруванням» якісних ознак – з приписуванням градаціям якісних змінних числових міток. Такий підхід дозволяє розповсюдити на якісні дані методи багатовимірного статистичного аналізу, розроблені відносно кількісних змінних.

Іноді необхідно побудувати систему міток, що забезпечує максимум коефіцієнта кореляції між двома змінними (оптимальні мітки). Ця система міток і відповідна їй матриця кореляції використовується потім для факторного і регресійного аналізу. Знаходження оптимальних міток пов'язане з перетворенням частот таблиці в частоти двовимірного нормального розподілу, оскільки кореляція перетвореного розподілу не може за абсолютною величиною перевищувати кореляцію двовимірного нормального розподілу. Перетворені таким чином змінні називають канонічними змінними. Розглянемо використання оптимальних міток для аналізу структури даних – виділення в таблиці спряженості лінійних і нелінійних ефектів. Звичайно при вивченні таблиці спряженості не робиться ніяких припущень щодо характеру зв'язку змінних, тоді як в конкретних дослідженнях буває важливо зрозуміти, чи відповідає фактичний розподіл гіпотезі, що висувається, – наприклад, гіпотезі про наявність лінійного зв'язку – чи ні, чи є розузгодження фактичних і теоретичних частот випадковими чи дійсно зв'язок змінних включає ряд складних взаємозв'язків.

Дослідити це питання дозволяє критерій χ2 через адитивні компоненти, які відповідають лінійним і нелінійним ефектам в структурі зв'язку між змінними. При цьому лінійні ефекти пов’язують з першим перетворенням змінних, нелінійні – з другим і т.д. перетвореннями. Адитивність ефектів випливає з ортогональності канонічних змінних.

Покажемо, що канонічний аналіз таблиці зв'язаності відповідає розкладанню статистики χ2 на ряд доданків, число яких залежить від розмірності таблиці. Перетворимо вираз таким чином:

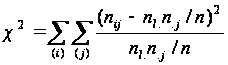(3.1)

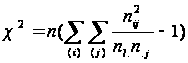(3.2)

Остання формула може бути подана за допомогою суми діагональних елементів, тобто слід симетричної матриці 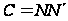, де N - матриця розмірності (m Ч p) з елементами 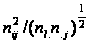(m – число рядків таблиці, p – число стовпців):

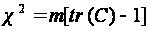(3.3)

Якщо число рядків таблиці не дорівнює числу стовбців, то, як правило, матрицю С формують так, щоб її розмірність була мінімальною (min(m,p)). Оскільки слід матриці дорівнює сумі її власних чисел, то вираз (3.3) приймає наступний вигляд:

(3.4)

де λk - k-е власне число матриці С.

Враховуючи, що власні числа є показниками кореляції (R2) між кожною парою канонічних змінних, виділених з вихідних наборів даних, запишемо рівність (3.4) у вигляді:

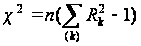(3.5)

З m (або p) власних чисел матриці С максимальне завжди дорівнює одиниці, йому відповідає вироджений набір міток 1 = (1,...,1). Тому вираз (3.5) доцільно переписати так :

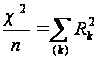(3.6)

Найбільше з чисел, що залишилися (m - 1) або (p - 1) власних чисел відповідає гіпотезі лінійності зв'язку між категоризованими змінними; наступне за величиною значення λk відповідає гіпотезі про складніший характер взаємозв’язку змінних. Така інтерпретація компонент χ2 представляється можливою з причини того, що кожна подальша пара канонічних змінних є функцією першої перетвореної пари, а все розкладання χ2 є спадаючою послідовністю.

Можна показати, що традиційні методи зв'язків, засновані на критерії χ2, змішують різні за характером зв'язки і знайдена міра є середньою з різних зв'язків, що ігноруються за однією таблицею. Це випливає з виразу (3.6), який дозволяє будь-який показник щільності зв'язку подати через канонічні кореляції. Наприклад, коефіцієнт взаємної спряженості Чупрова виглядатиме так:

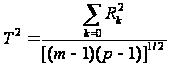(3.7)

Таблиці 2Ч2 виділяються два власних числа матриці С. Оскільки перше дорівнює одиниці, то квадрат канонічної кореляції дорівнює квадрату коефіцієнта спряженості Пірсону:

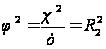(3.8)

Канонічні змінні дозволяють одержати якнайкраще, в сенсі деякого критерію, наближення коміркових частот таблиці спряженості. Як показали М. Кендалл і А. Стьюард, кожна спостережувана комірка може бути розбита на теоретичну частоту, яка відповідає гіпотезі про незалежність змінних, і адитивний внесок, пов'язаний з канонічною кореляцією:

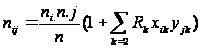(3.9)

де хik – канонічна мітка для і-ого рядка к-го власного числа; yjk – канонічна мітка для j-го стовпця і к-го власного числа.

Відповідно є можливість подати вихідну таблицю спряженості у вигляді серії таблиць, кожна з яких відповідає певній гіпотезі зв'язку змінних (тобто частоти таблиці, обчислені при тому або іншому власному числі λk матриці С).

Існує ряд способів знаходження канонічних міток. Найшвидше приводить до мети наступний порядок дій: спочатку визначаються хik діленням кожної компоненти відповідного власного вектора на корінь квадратний з маргінальної частки; потім визначаються yjk – шляхом усереднювання міток рядків для кожного j - й стовпця.

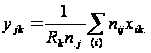(3.10)

Набори міток хik і yjk, зважені за відповідними маргінальними частотами, мають нульові середні й одиничні дисперсії.

4. Побудова логарифмічної моделі

Логарифмічно лінійна модель системи з трьох змінних запишеться у вигляді:

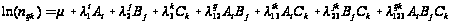λijkABC (4.1)

де ln(nijk) – очікувана частота чарунка (і, j, k) тривимірної таблиці спряженості, обчислена за умови незалежності змінних A, B, C; параметри λ визначають внесок у логарифм очікуваної частоти змінних як окремо , так і внаслідок їхньої взаємодії. Параметри λ логлінійної моделі задовольняють умовам:

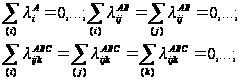(4.2)

Оцінки параметрів обчислюються за методом максимальної правдоподібності:

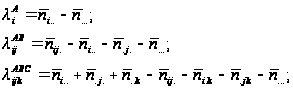(4.3)

Точка в індексі означає середнє значення за цим індексом, так:

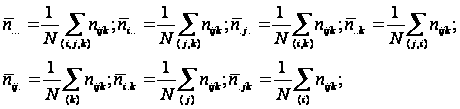(4.4)

де nijk - частота комірки (і, j, k), яка спостерігається N – число комірок таблиці спряженості.

Оцінка дисперсії параметра λ для насиченої моделі дорівнює

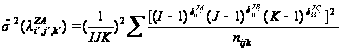(4.5)

де δiiZA = 1, якщо А належить групі змінних Z и 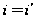, в супротивному разі δiiZA = 0. Аналогічно обчислюються δjjZB, δkkZC.

Якщо поділити, знайдену в результаті розрахунків оцінку на оцінку його середнє квадратичного відхилення 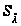, то одержимо стандартизоване значення оцінки параметра. Це значення може бути використане для порівняння відносного внеску кожного параметра в nijk, тим самим для обчислення порівняльного значення впливу окремих змінних, кожному парний і множинному взаємозв'язки.

Відзначається, що, крім з насиченої моделі стандартизовані параметри , рівні нулю, можна перейти до моделі, більш адекватної вихідних даних або апріорним припущенням про відносини між змінними.

Одержуємо модель ієрархічну за побудовою, оскільки модель врахована множинна взаємодія A, B, C, а це означає припущення існування зв'язків у будь-якій підгрупі зі складових "старших" взаємозв'язок (ABC) змінних, і тому в модель включені такі параметри, як λAB, λBC, λAC, λA, λB, λC. Якщо ж передбачається, що між змінними немає взаємозв'язків, то у модель не включається відповідний параметр λ . Порядок логлинейной моделі дорівнює найбільшому числу змінних.

Побудова моделі складається з наступних основних етапів: 1) означення порядку логлінійної моделі; 2) відбір параметрів заданого порядку для включення в підсумкову модель.

Логлінійна модель має порядок к, якщо будь-які до к + 1 і більше змінних одночасно незалежні. Тому для означення порядку моделі перевіряються гіпотези про незалежність будь-яких до к + 1 і більш змінних за допомогою критеріїв 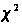и 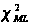(максимальної правдоподібності). Число ступенів вільності для обох статистик дорівнює n-p, де n – число всіх комірок таблиці, а p – число оцінюваних очікуваних частот за умови незалежності змінних.

Крім того, для кожного к-го порядку перевіряється гіпотеза про одночасну незалежність відповідних ним змінних за допомогою цих же критеріїв.

Так, для параметрів третього порядку перевіряється гіпотеза про відсутність потрійної взаємодії.

Спільна перевірка викладених вище гіпотез дозволяє визначити порядок моделі, що щонайкраще відбиває структуру взаємозв'язків змінних.

Наступним етапом є відбір параметрів моделі, тобто включення в модель тільки тих параметрів, які відбивають істотні впливи й взаємодії змінних. Для розв’язання цієї задачі (перевірки відповідної гіпотези) використовується критерій .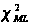

Спочатку обчислюється різниця значень критеріїв 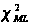, розрахованих відповідно для насиченої моделі к-го порядку й моделі, що відрізняється від насиченої моделі параметром, який перевіряється на значущість. Критерій, побудований у такий спосіб називається критерієм приватного зв'язку змінних. Критерій 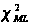для маргінального зв'язку будуватися подібним чином лише з тією різницею, що його значення обчислюються за таблицею, знайденою підсумовуванням частот вихідної багатомірної таблиці спряженості за критеріями змін, що не входять у досліджуваний на значущість параметр. Число ступенів вільності для критеріїв частинного й маргінального зв'язку для групи змінних Z обчислюється за формулою :

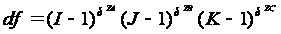(4.6)

де I, J, K – число рівнів ознак A, B, C відповідно, δZA = 1, якщо А входить в Z, і а якщо ні, то δZA = 0 і т. п.

Критерії частинного і маргінального зв'язків еквівалентні за λ параметрами, які представляють вплив окремо взятих змінних. Відбір параметрів проводитися за наступним правилом: а) якщо обидва критерії (частинного і маргінального зв'язку) показують значущість параметра, то він не виключається з початкової повної моделі; б) якщо обидва критерії вказують на його незначущість, то параметр виключається з моделі; в) якщо ж за одним з критеріїв параметр значущий, а за іншим - ні, то необхідно проводити спеціальне дослідження.

Висновки

Логлінійний аналіз – це статистичний аналіз зв’язку таблиць спряженості за допомогою логлінійних моделей. Логлінійна модель для трьох змінних має вигляд:

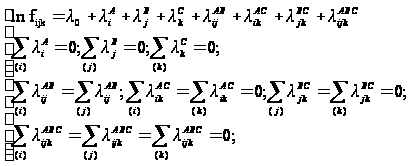
де fijk,λ – невідомі параметри, які називаються:

λiA – ефект i-ого рівня ознаки А, i=1,..,I;

λjB - ефект j -ого рівня ознаки B, j=1,..,J;

λkC - ефект k-ого рівня ознаки C, k=1,..,K;

λijAB – ефект взаємодії i-ого рівня ознаки А та j -ого рівня ознаки B;

λikAC – ефект взаємодії i-ого рівня ознаки А та k-ого рівня ознаки C;

λjkBC - ефект взаємодії j -ого рівня ознаки B та k-ого рівня ознаки C;

λijkABC – ефект взаємодії i-ого рівня ознаки А, j -ого рівня ознаки B та k-ого рівня ознаки C;

fijk - гіпотетична частота в (i,j,k)-ій комірці

Оцінки параметрів знаходяться за методом максимальної правдоподібності й набувають вигляду:

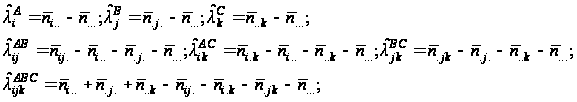
де

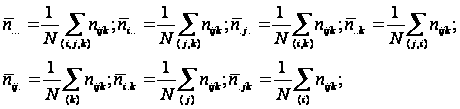
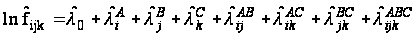
Для перевірки гіпотез

H0: λijAB=0, i=1,..,I, j=1,..,J – про незалежність ознак А і В;

H0: λikAC=0, i=1,..,I, k=1,..,K – гіпотеза про незалежність ознак А і C;

H0: λjkBC=0, j=1,..,J, k=1,..,K – гіпотеза про незалежність ознак B і C;

H0: λijkABC=0, i=1,..,I, j=1,..,J, k=1,..,K – гіпотеза про незалежність ознак A, B і C

використовують критерій 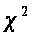та критерій частинного зв’язку ознак.

Критері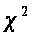й . Якщо гіпотезу Н0 відхиляти при:

і не відхиляти в супротивному разі, то з імовірністю α гіпотеза відхиляється, коли вона справедлива. n – кількість всіх комірок, p - число оцінюваних очікуваних частот при умові незалежності змінних,

Критерій частинного зв’язку ознак. Якщо гіпотезу Н0 про взаємозв’язок ознак А і В відхиляти при

і не відхиляти в супротивному разі, то з імовірністю α, гіпотеза відхиляється, коли вона справедлива.

Якщо гіпотезу Н0 про взаємозв’язок ознак А і C відхиляти при

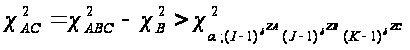
і не відхиляти в супротивному разі, то з імовірністю α, гіпотеза відхиляється, коли вона справедлива.

Якщо гіпотезу Н0 про взаємозв’язок ознак В і C відхиляти при

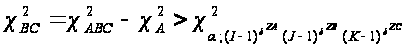
і не відхиляти в супротивному разі, то з імовірністю α, гіпотеза відхиляється, коли вона справедлива.

Список використаних джерел

Толстова Ю.Н. Анализ социологических данных: методология дескриптивная статистика, изучение связей между номинальными признаками, М.: Научный мир 2000.

Елисеева И.И., Рукавишников В.О. Логика прикладного статистического

анализа. М.,: Финансы и статистика, 1982.

Миркин Б.Г. Анализ качественных признаков и структур. М., 1980.

Мирзоев А.А. Применение логлинейного анализа для обработки данных социологических исследований, М.: АН СССР, 1980.