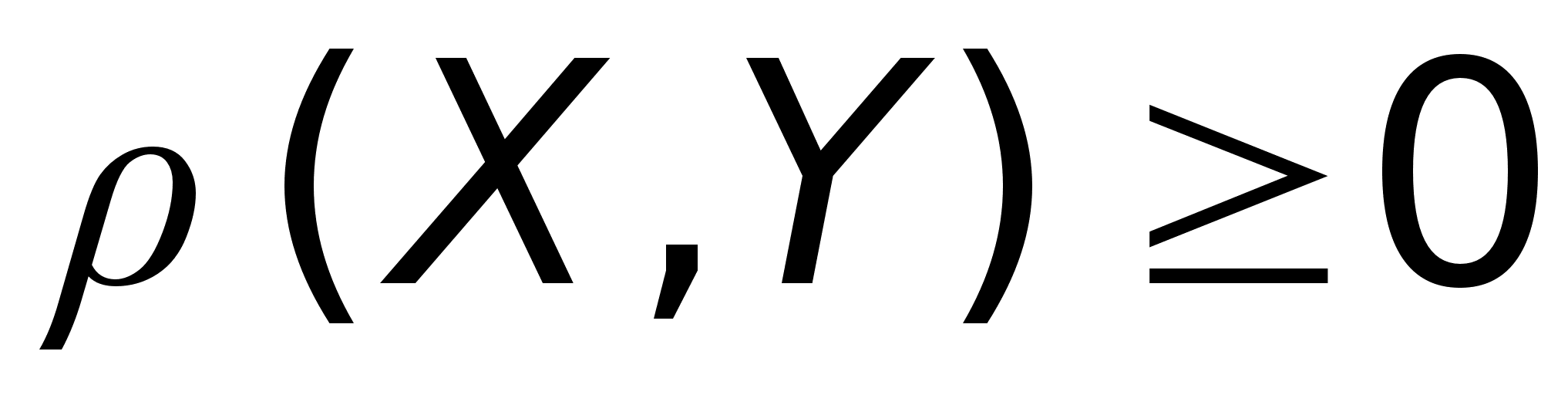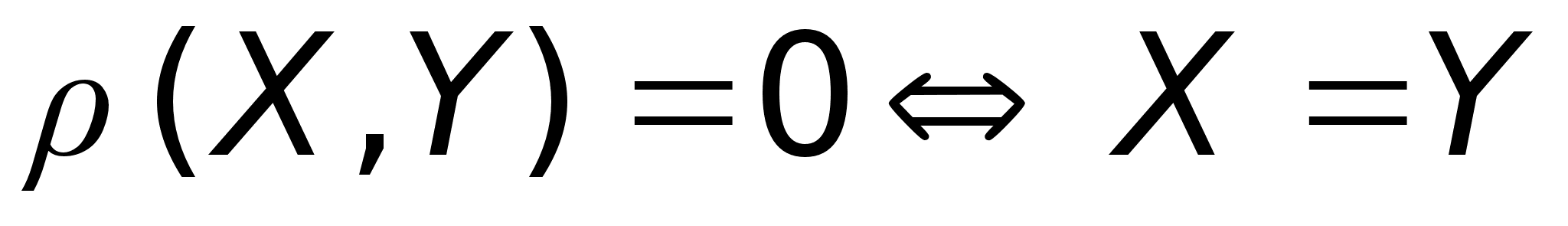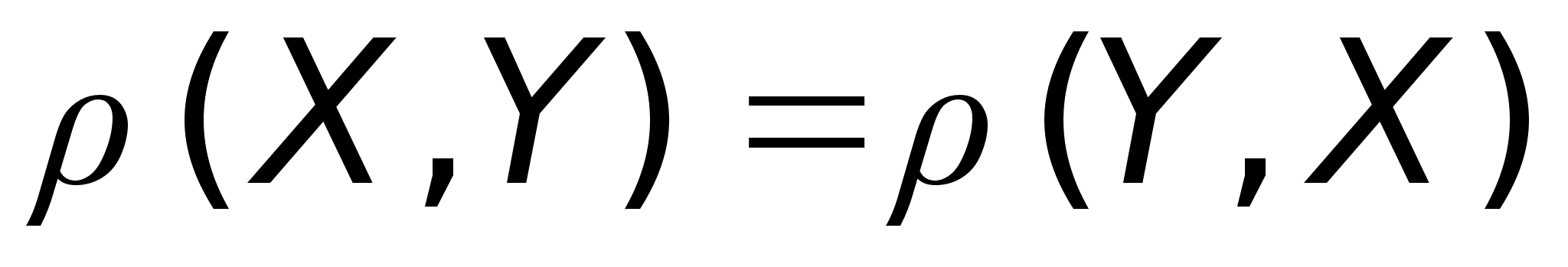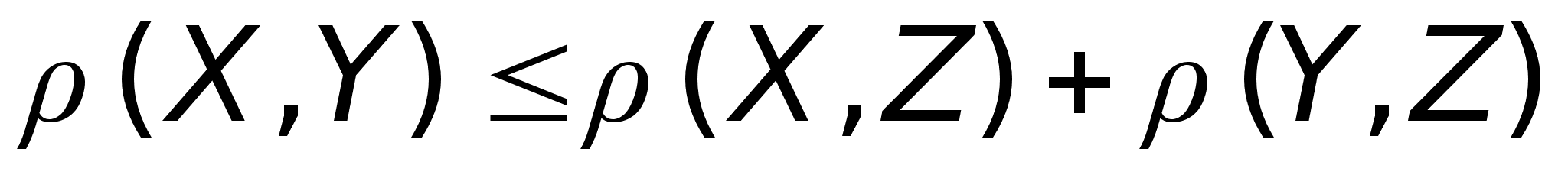Лекции по Математическому анализу
align="ABSMIDDLE" />
5. Пусть
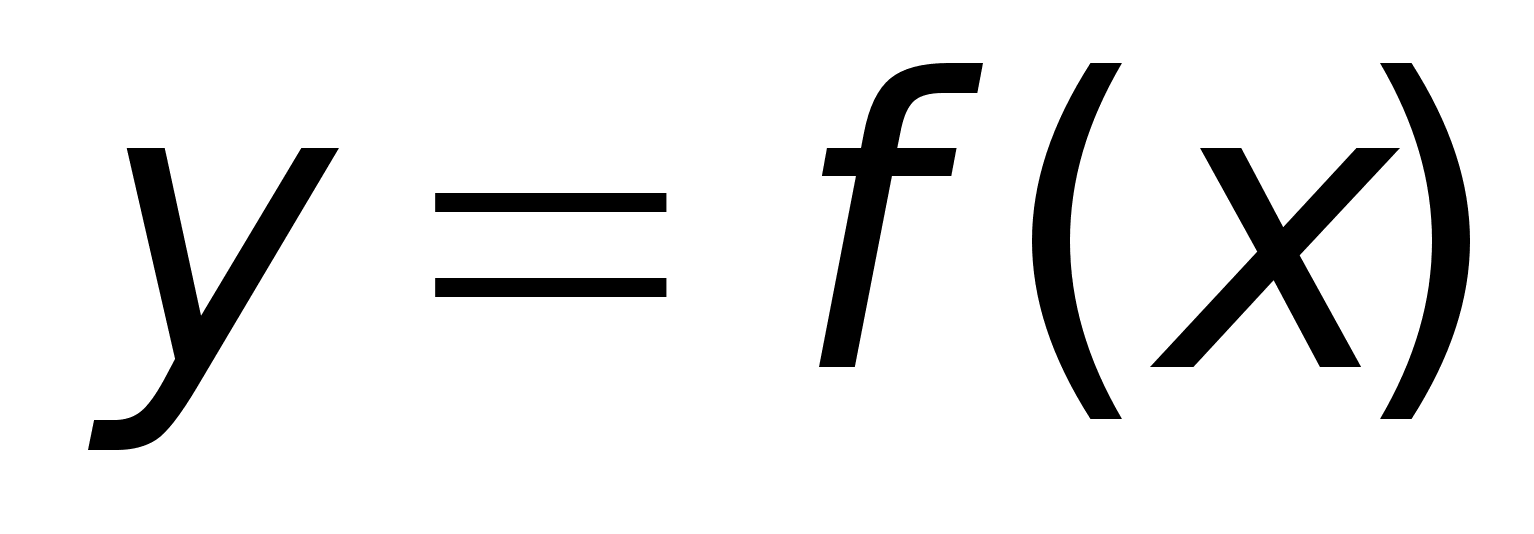 инт-ма на
инт-ма на
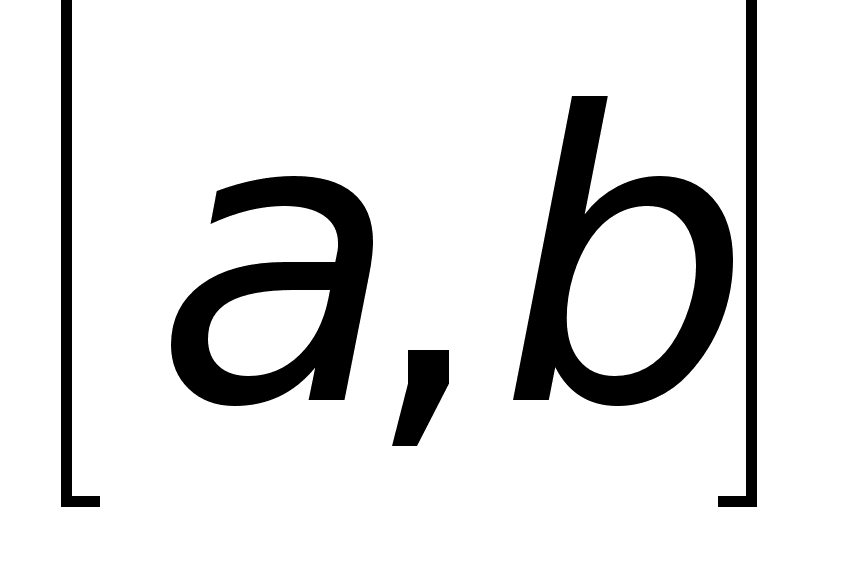
модуль ф-ии
тоже интегрируем
на
модуль ф-ии
тоже интегрируем
на
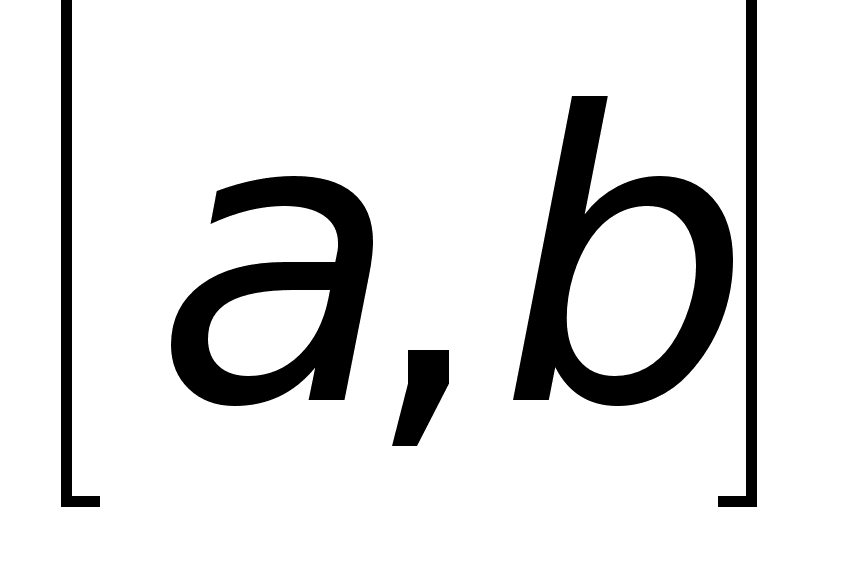 и справедливо
неравенство:
и справедливо
неравенство:
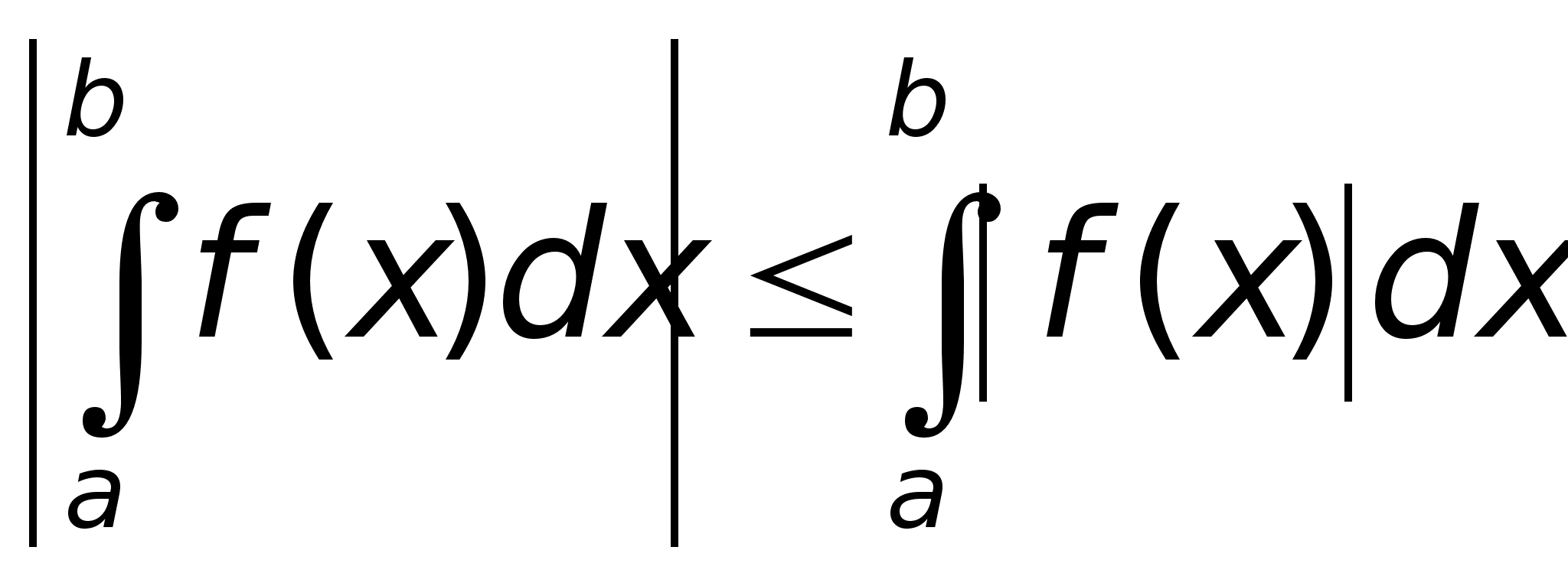
6. Пусть
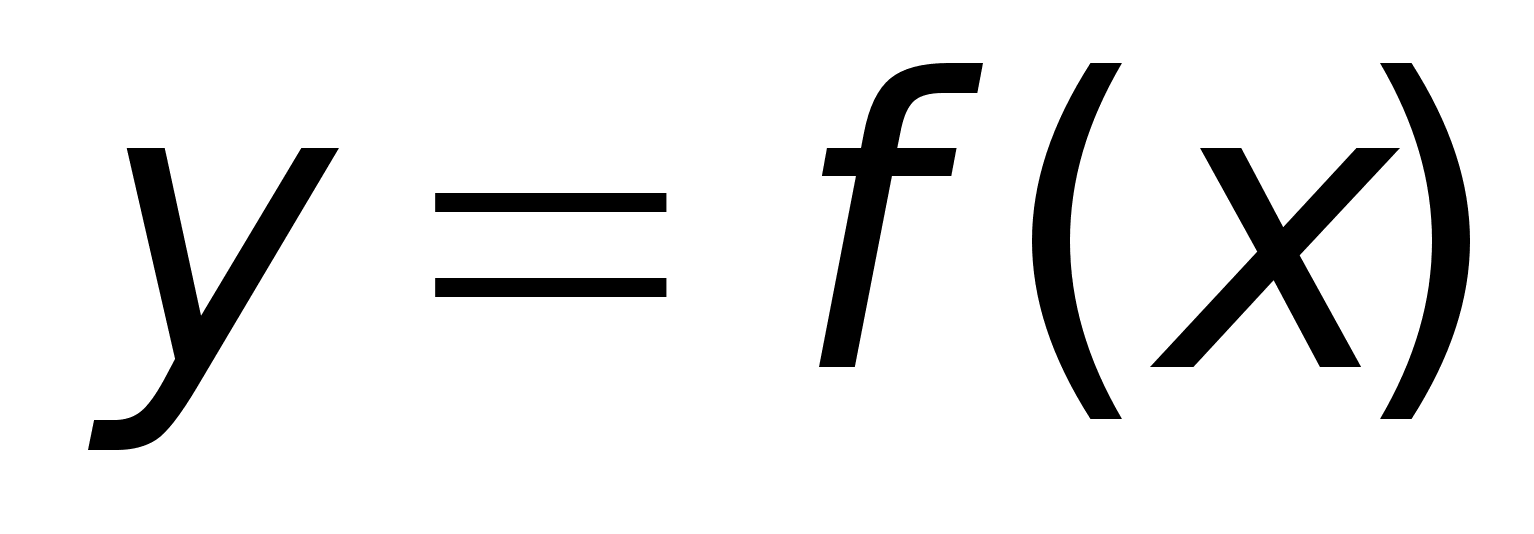 интегрируема
на
интегрируема
на
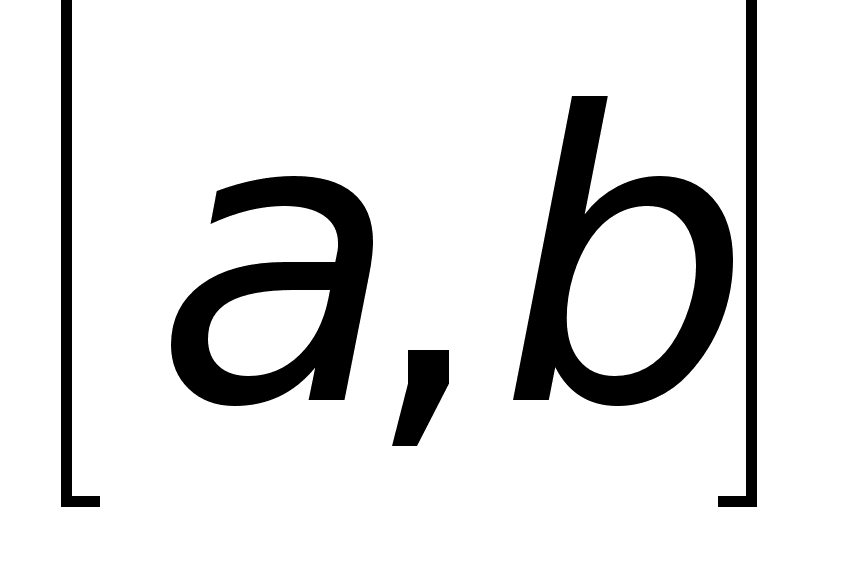 ,
,
 ,
то существует
М,
такая что
,
то существует
М,
такая что
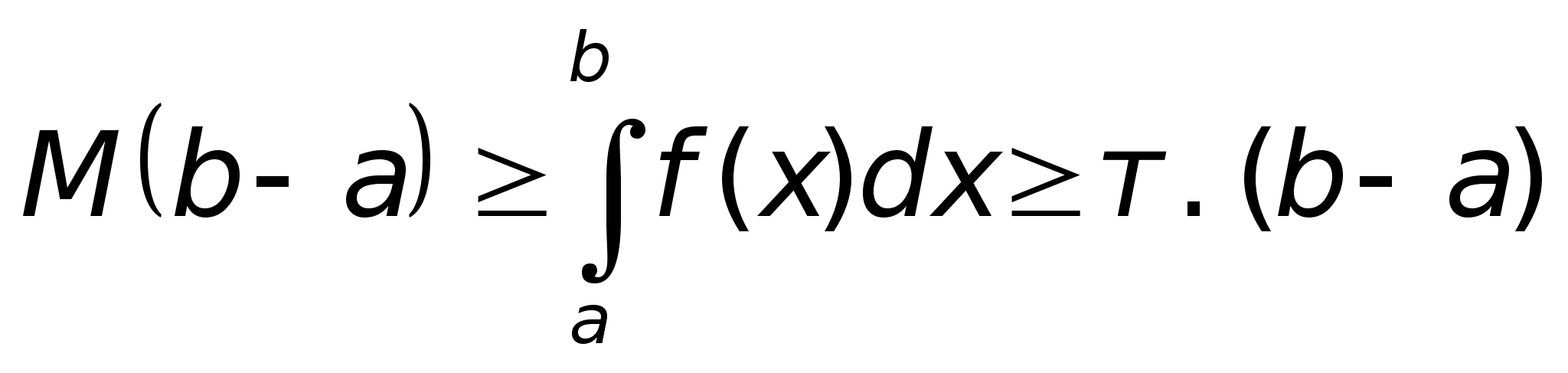
Интеграл как ф-ия переменного верх. предела.
Пусть ф-ия
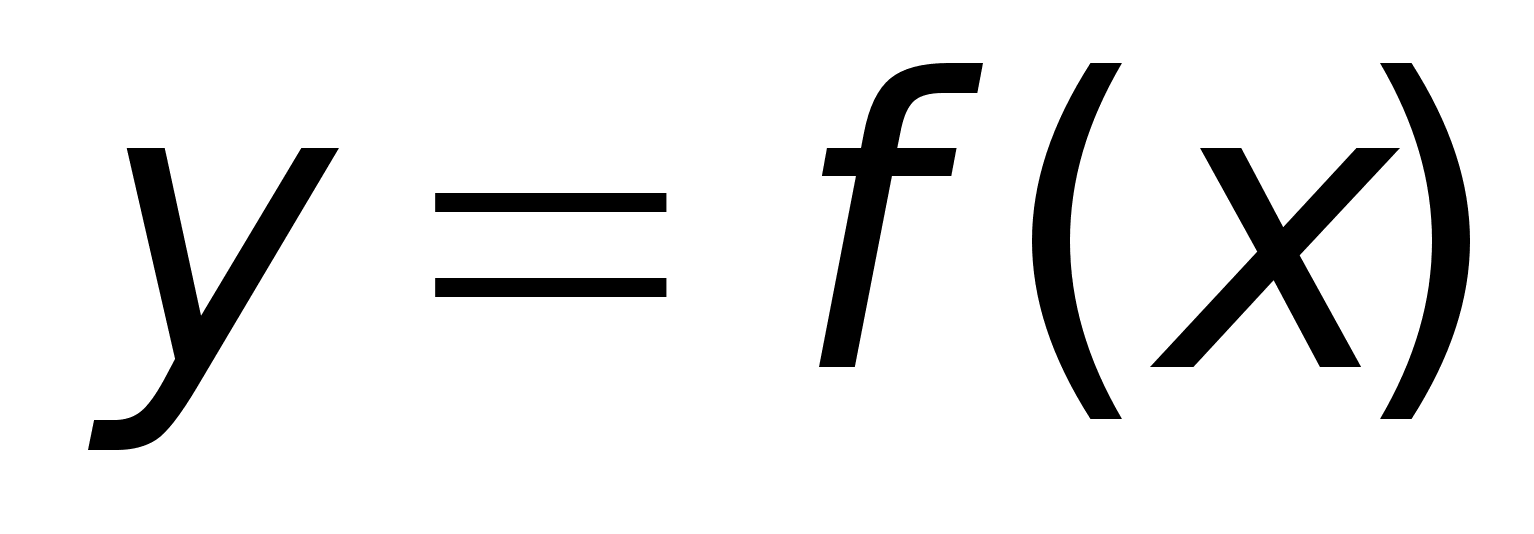 инт. на
инт. на
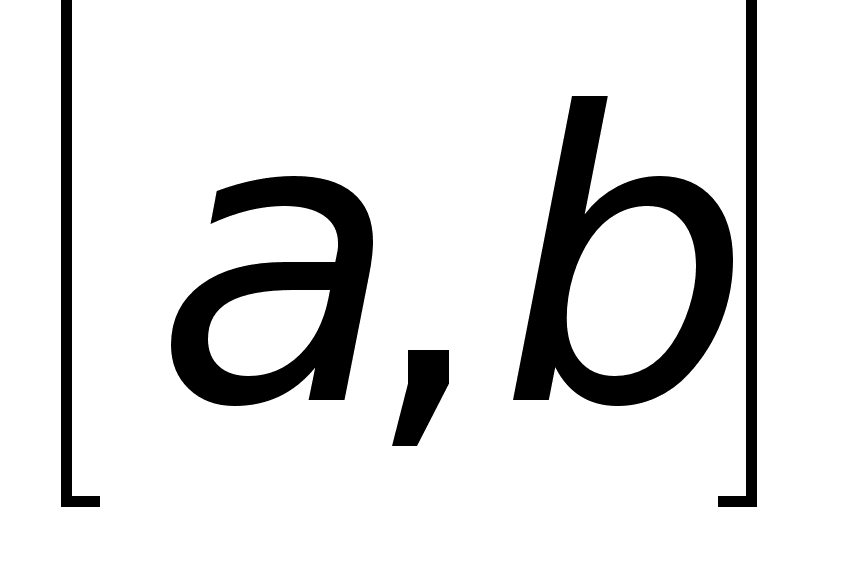 ,
,
 ,
то она инт. на
любом отрезке
между
,
то она инт. на
любом отрезке
между
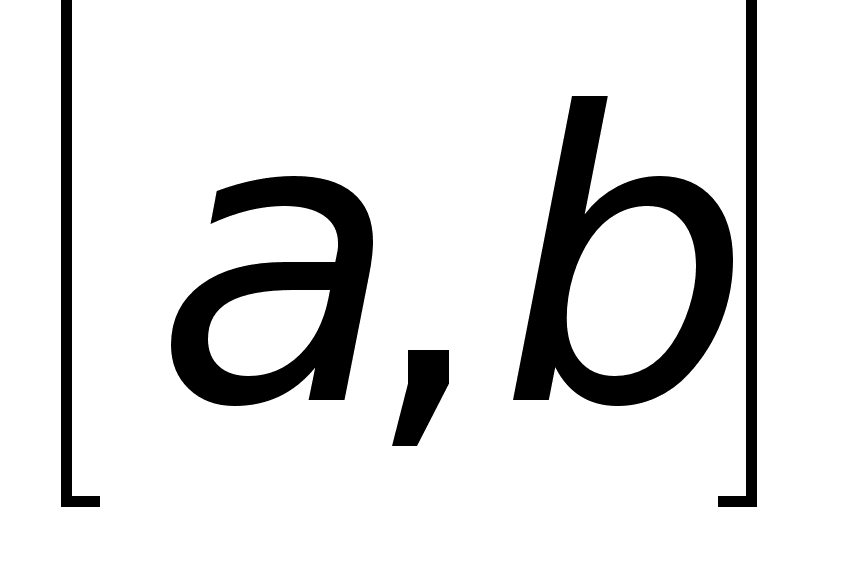
Рассмотрим
определенный
интеграл
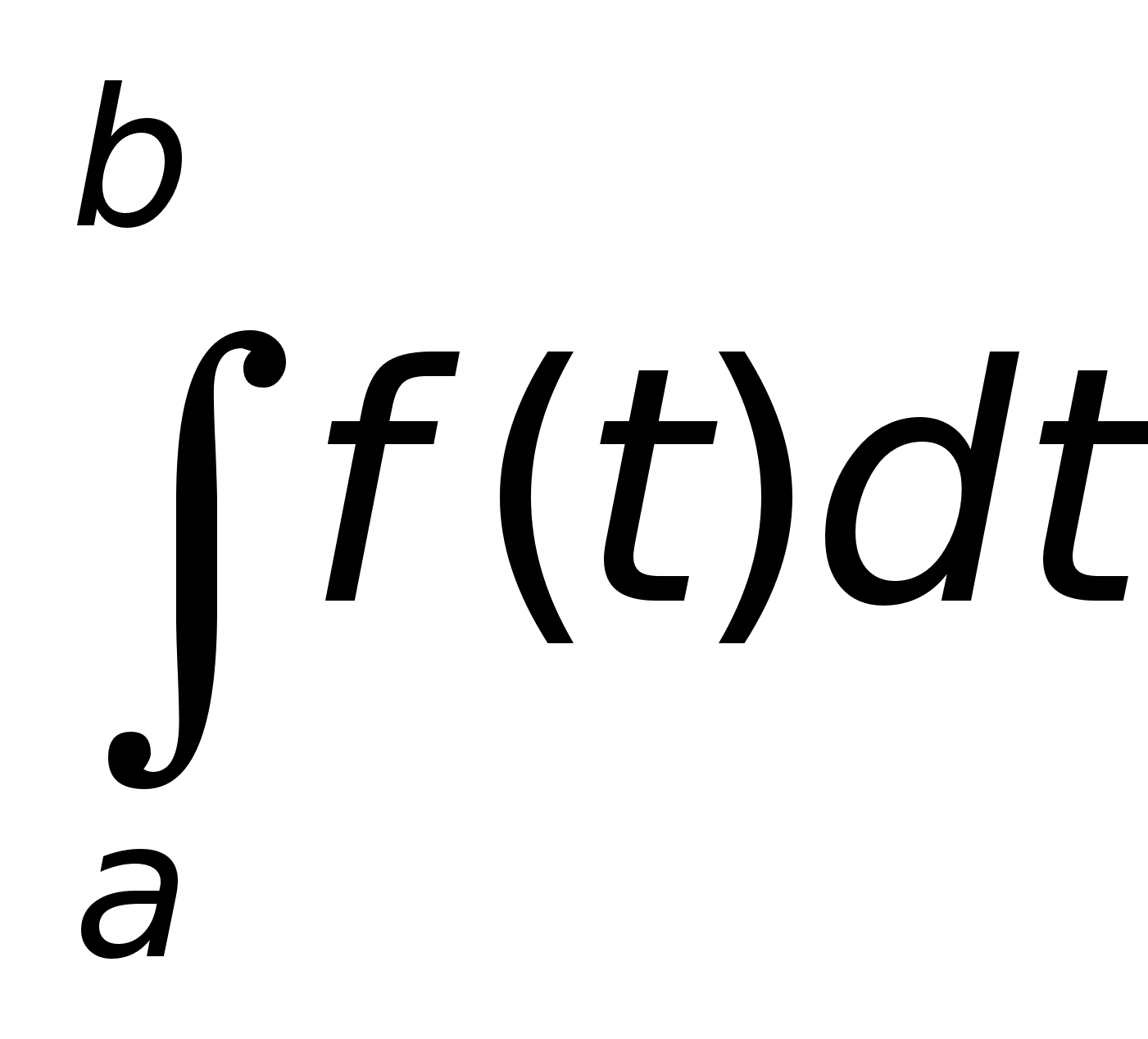 .
Из определения
опр. интеграла
следует,что
любому х
соот. единст.
значние этого
интеграла.
.
Из определения
опр. интеграла
следует,что
любому х
соот. единст.
значние этого
интеграла.
Определенный
интеграл с
перемнного
верх. предела
– есть ф-ия своего
предела
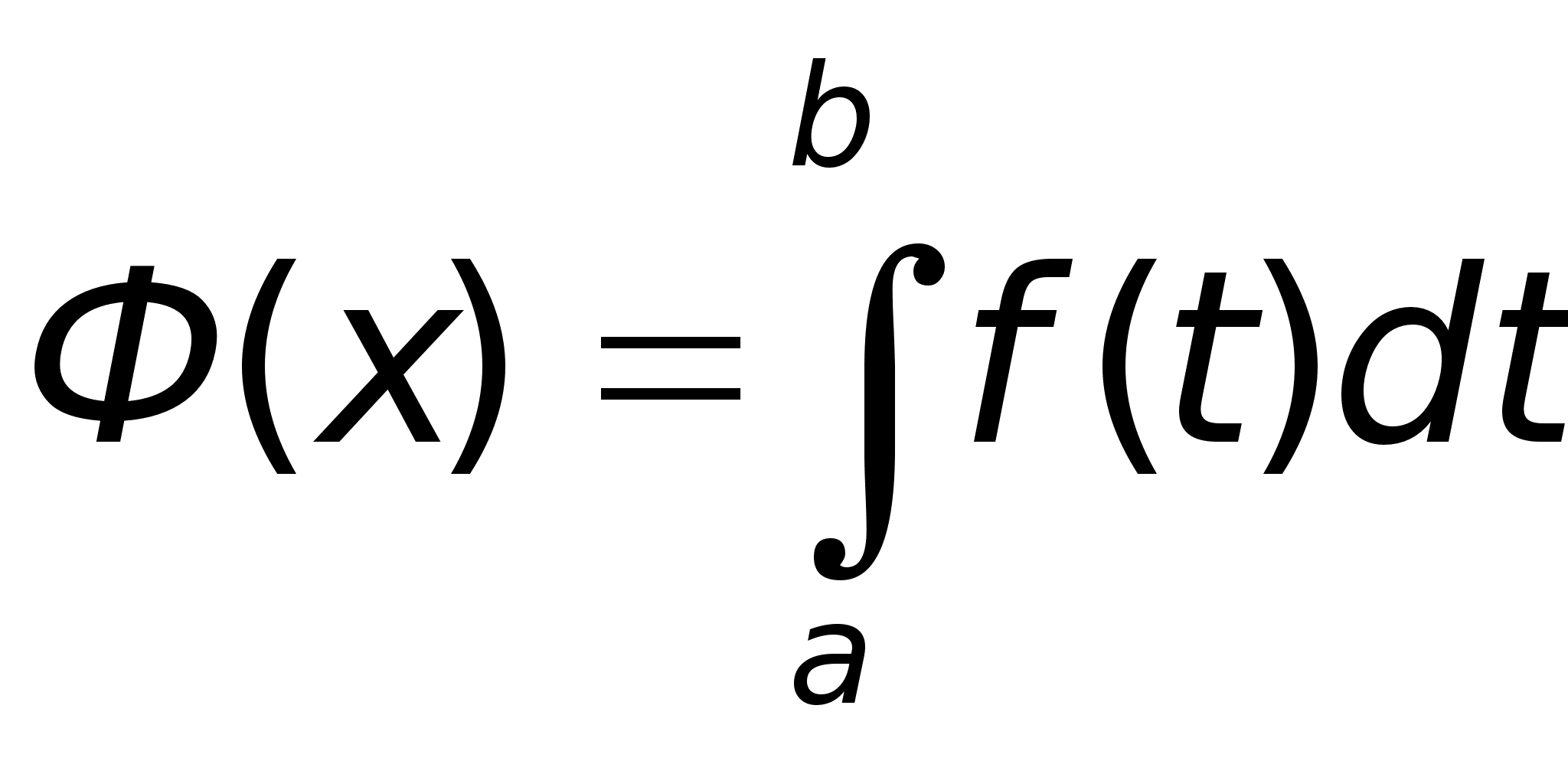
1 теорема Гульдена
Ph
Гульдена
Пусть криволинейная
трапеция вращ.
вокруг оси oX.
Тогда она опишет
тело вращения
с массой

из формулы
для центра масс
знаем:
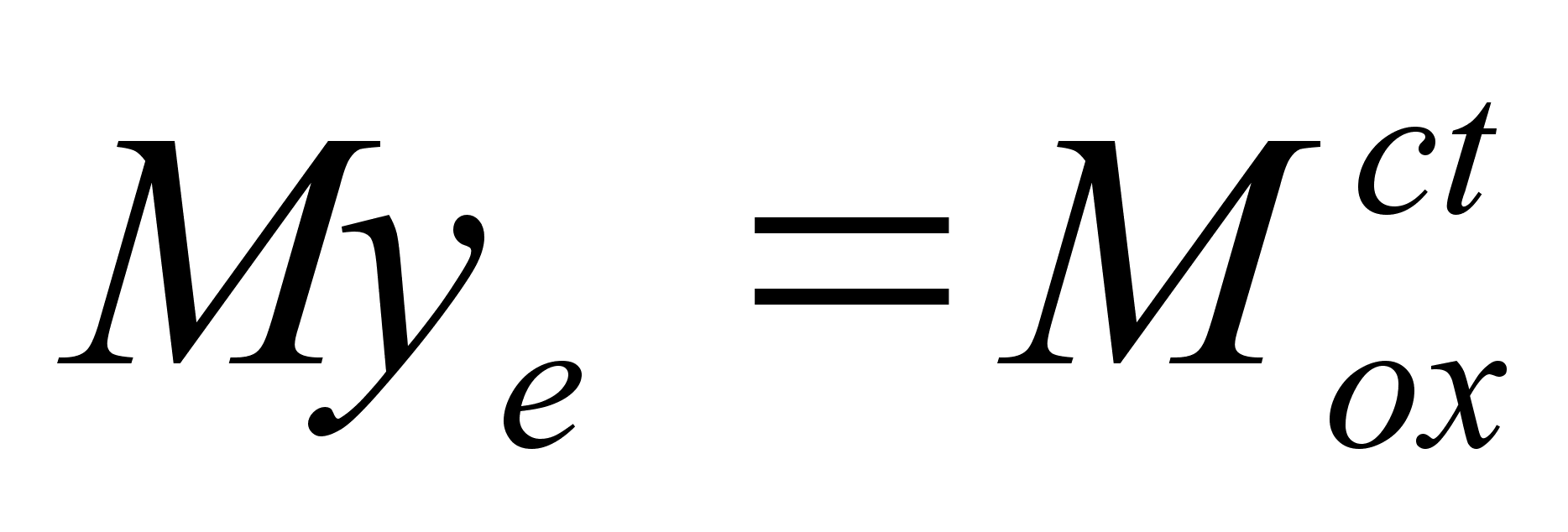
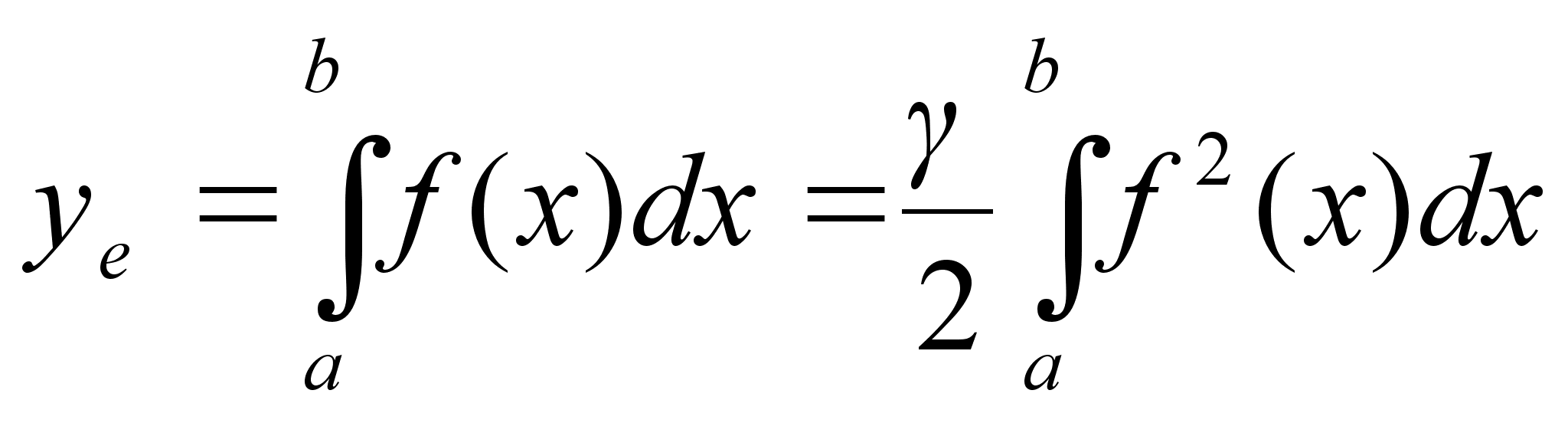
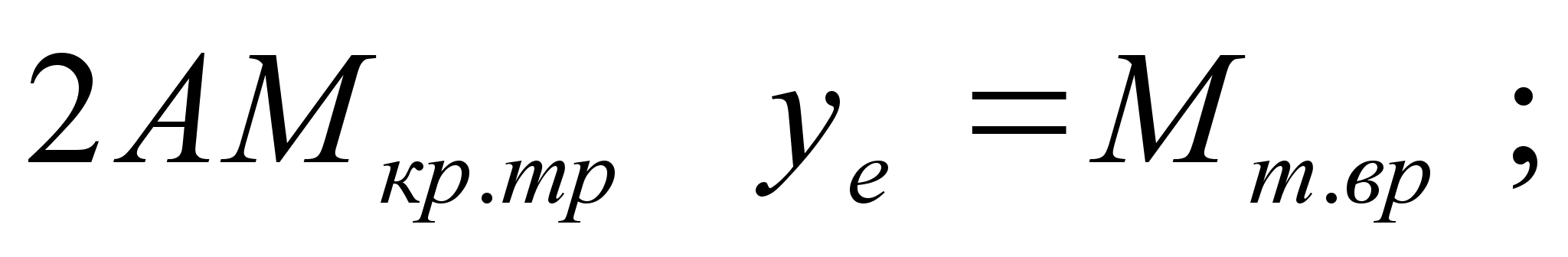

Объем тела, полученного вращением крив. трапеции, равно произведению площади этой трапеции на длину окружности, описанную из центра масс.
Однородная плоская дуга
От точки с
абсциссой х
отложим дугу
длины
 .
Тогда
.
Тогда
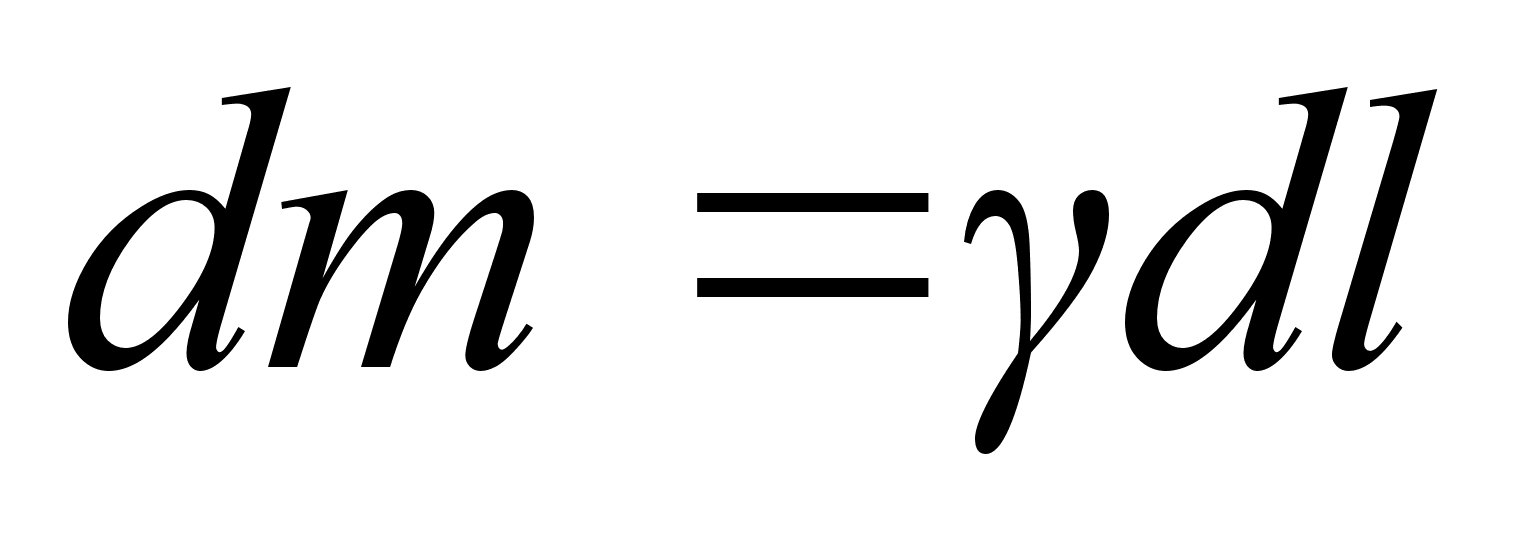 ,
,
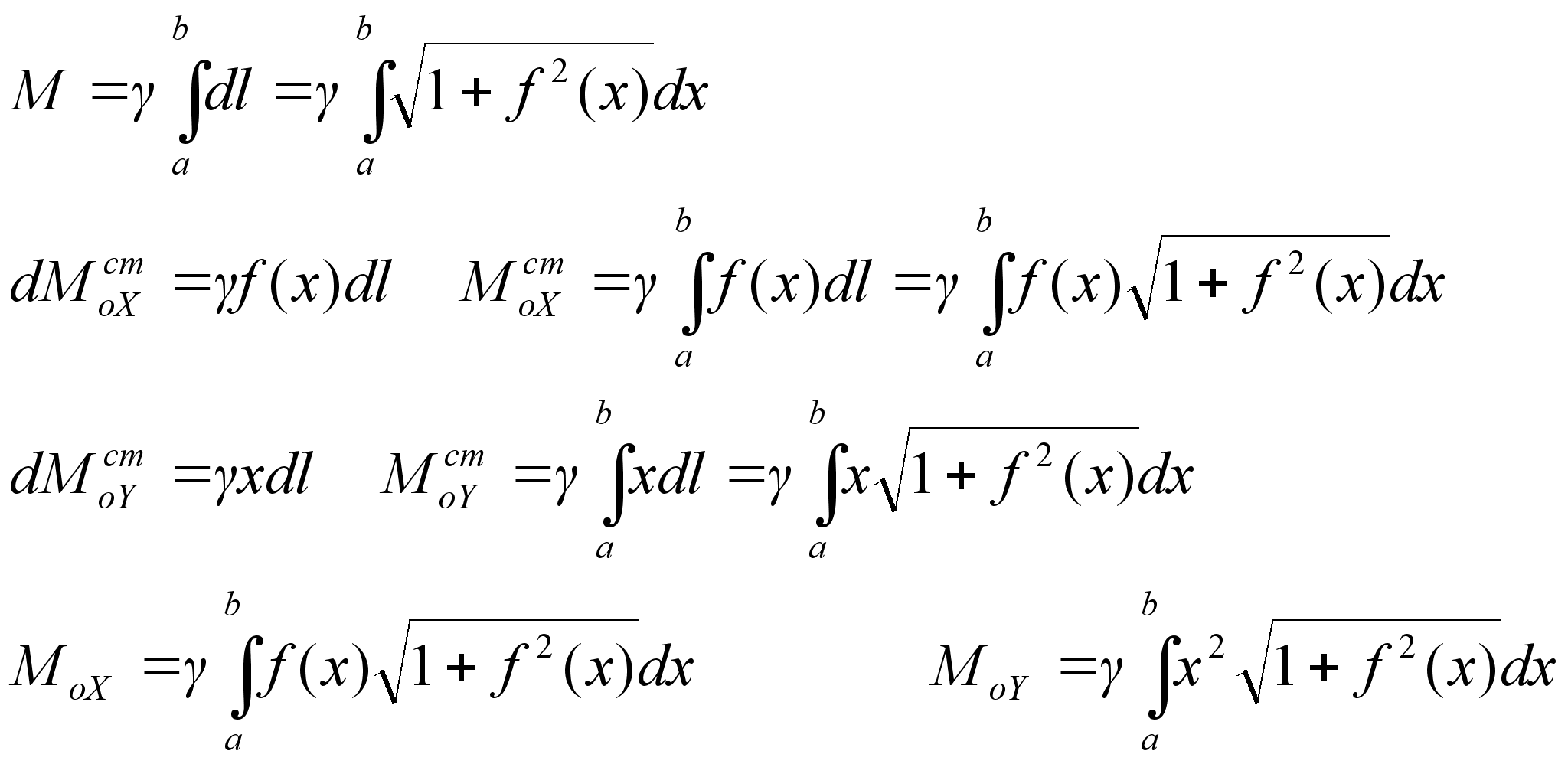
2 теорема Гульдена
Пусть плоская дуга вращается вокруг оси oX. Она опишет площадь:
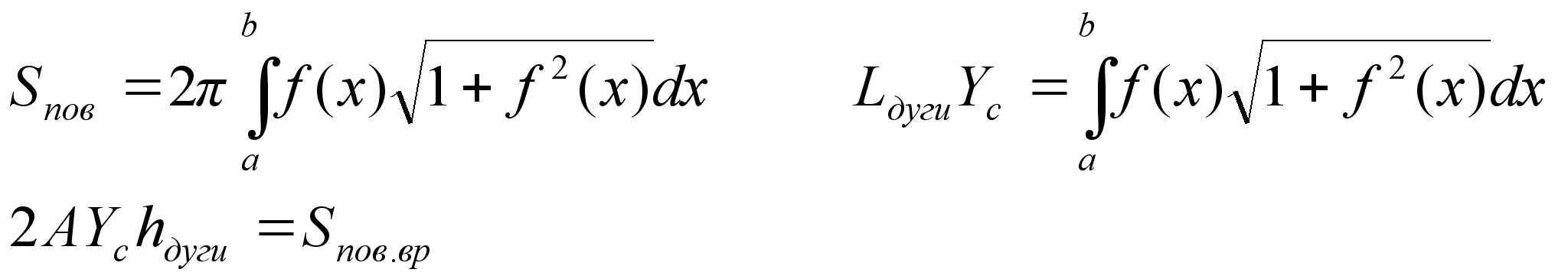
Площадь поверхности, полученная вращением дуги, равна произведению длины этой дуги на длину окр-ти, описыв-ю ц. масс.
Несобств. интегралы.
Для существования определенного интеграла должны выполняться два условия:
Предел интегрирования конечный;
Подынтегральная ф-ия ограничена.
Нарушение этих двух условий приводит к несуществующему интегралу.
В этом случае вводится обобщение определенного интеграла, который называется несобственным интегралом.
1. Несобственный интеграл с бесконечным пределом интегрирования.
а)
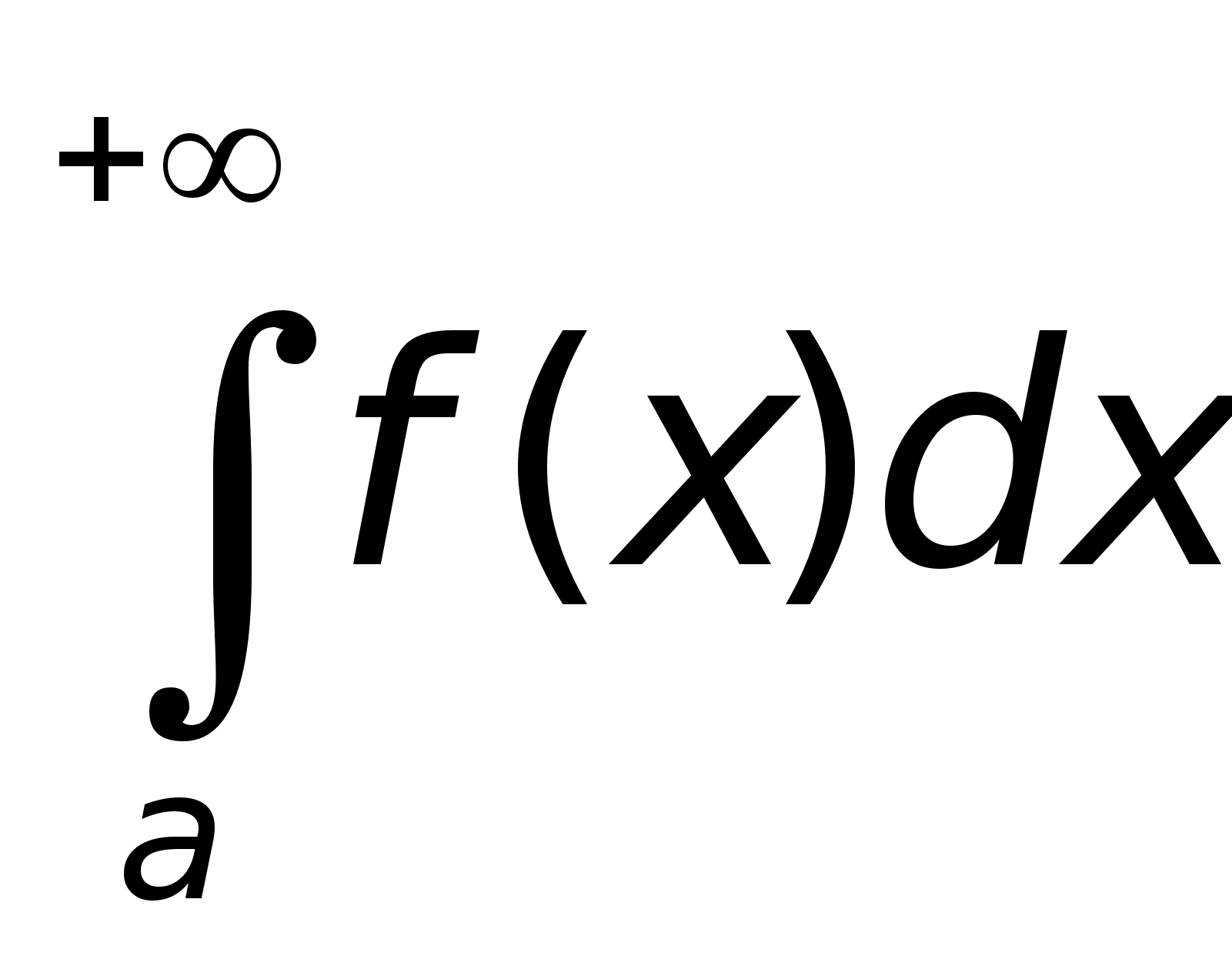 -
Пусть
-
Пусть
 -
интегрируема
на любом
-
интегрируема
на любом ,
где
,
где
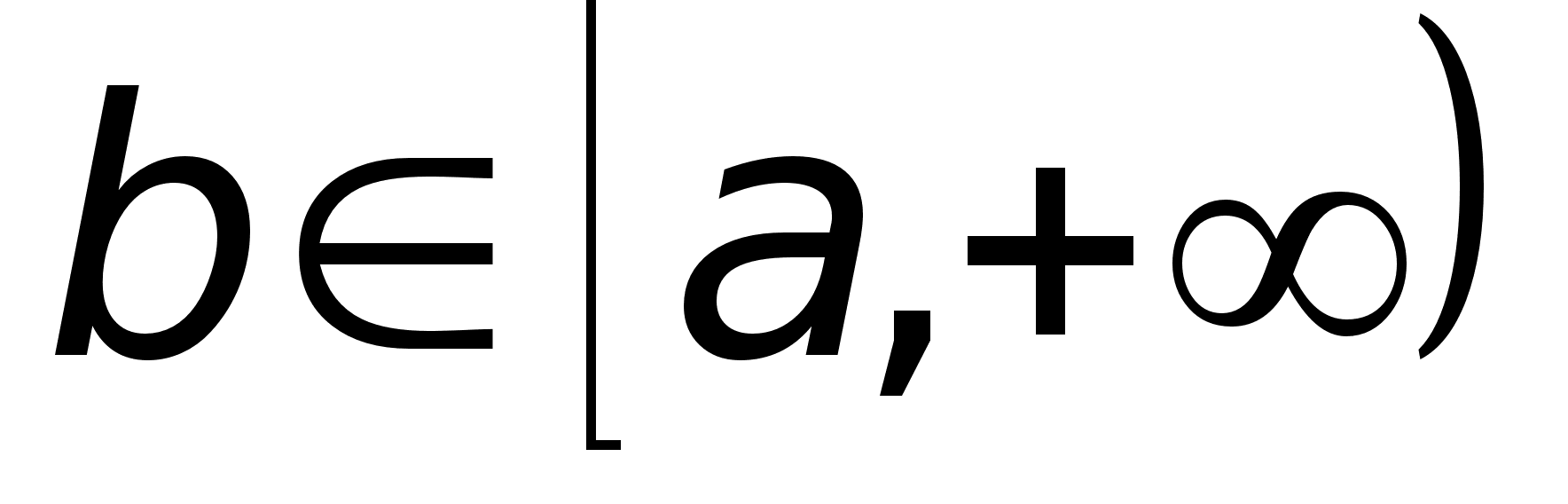 ,
то по определению:
,
то по определению:
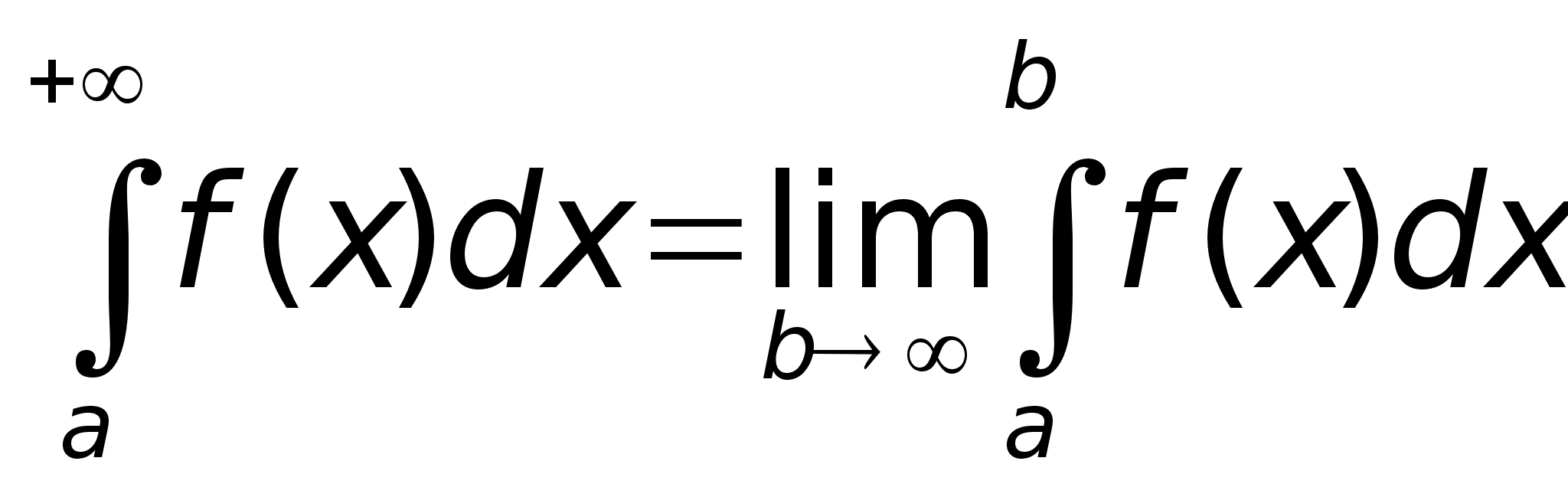
Если предел в правой части существует и конечен, говорят, что, инт. сходится; нет - расходятся.
б)
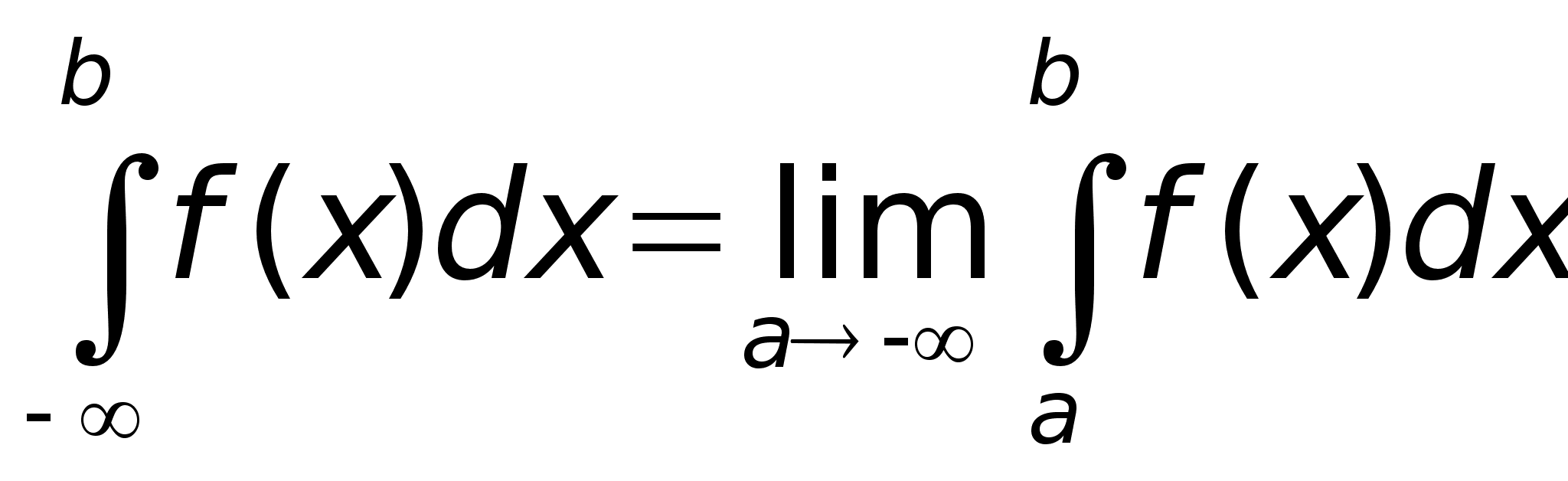
в)
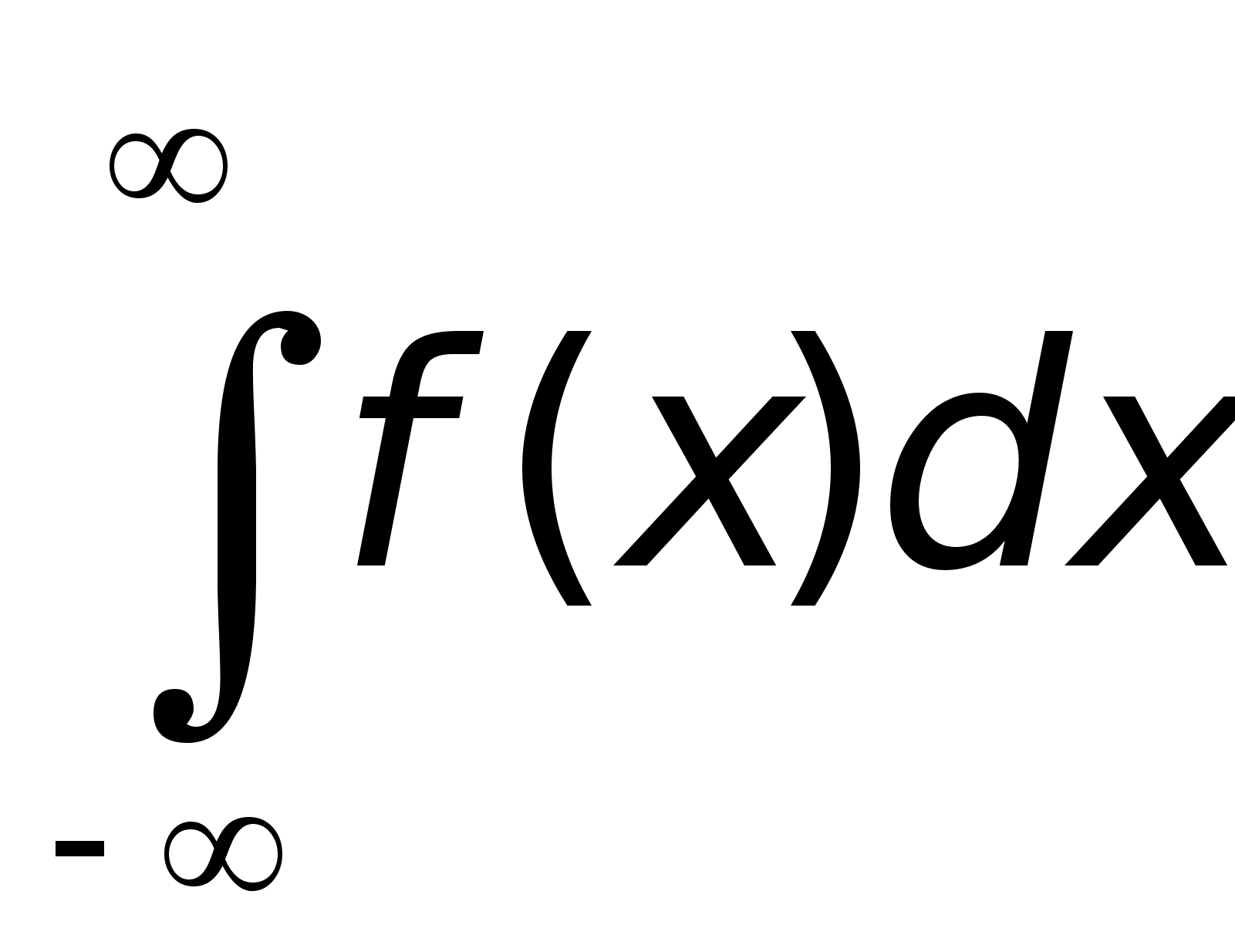 Этот случай
сводится к
предыдущему
***
Этот случай
сводится к
предыдущему
***
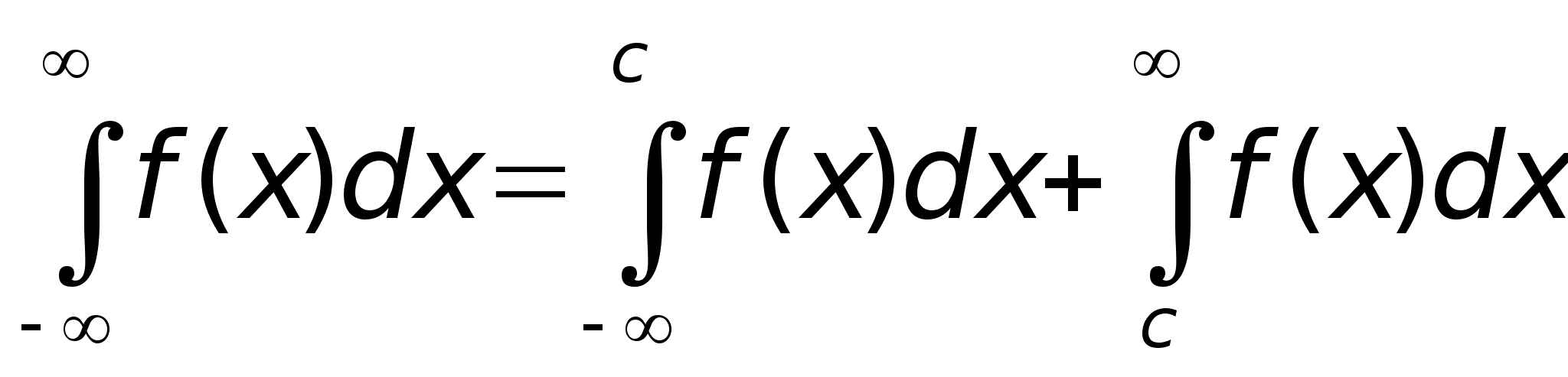 ,
,
 ;
Результат от
с не
зависит
;
Результат от
с не
зависит
Zm: Инт. в левой части существует, если интеграл в правой части существует по отдельности, т.е. предел интегрирования в этих интервалах надо обозначать разными буквами.
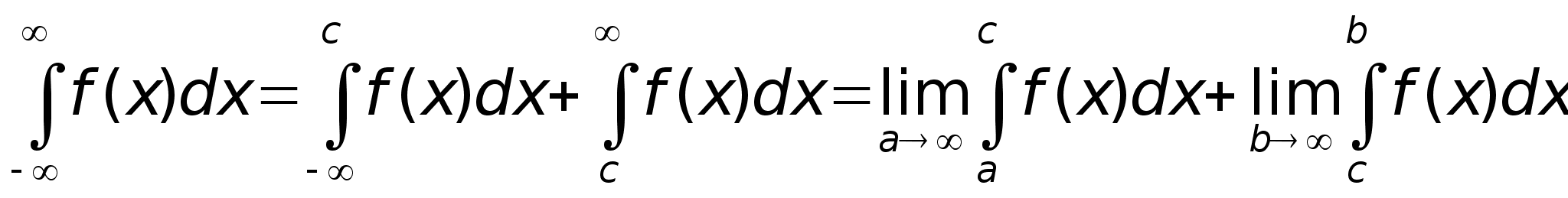
Признаки сходимости
В некоторых случаях достаточно знать, сходится интеграл или нет, без его вычисления. Для этого применяется признак сравнения.
1). Пусть
 и
и
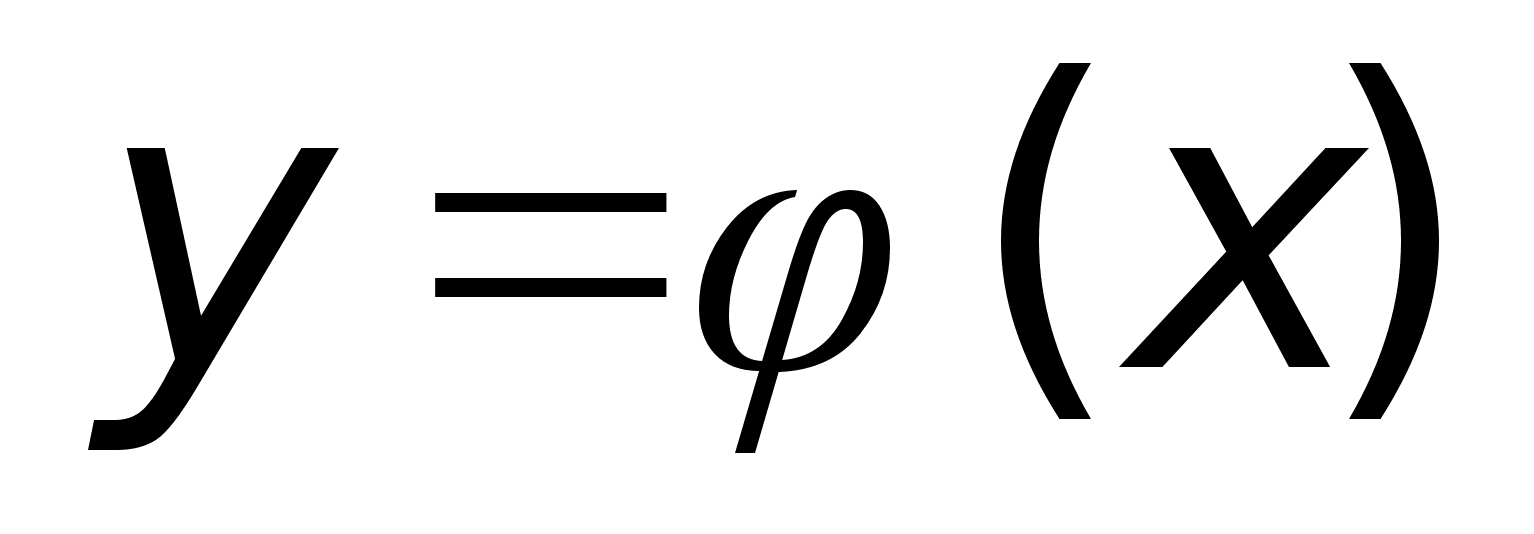 интегрируемы
на
интегрируемы
на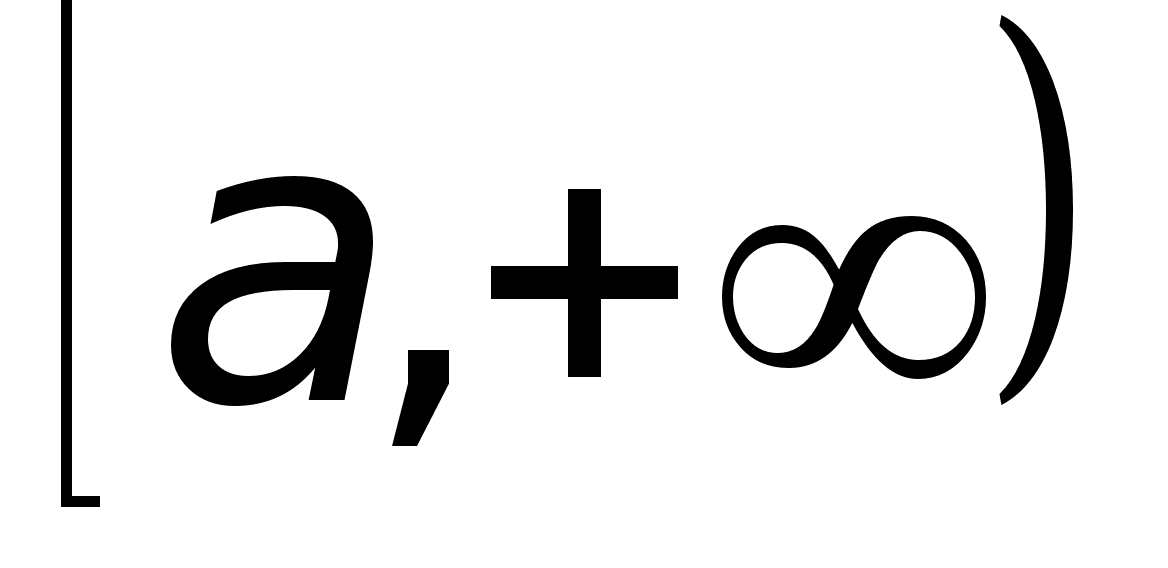 и
удовлетворяют
на этом промежутке
неравенству:
и
удовлетворяют
на этом промежутке
неравенству: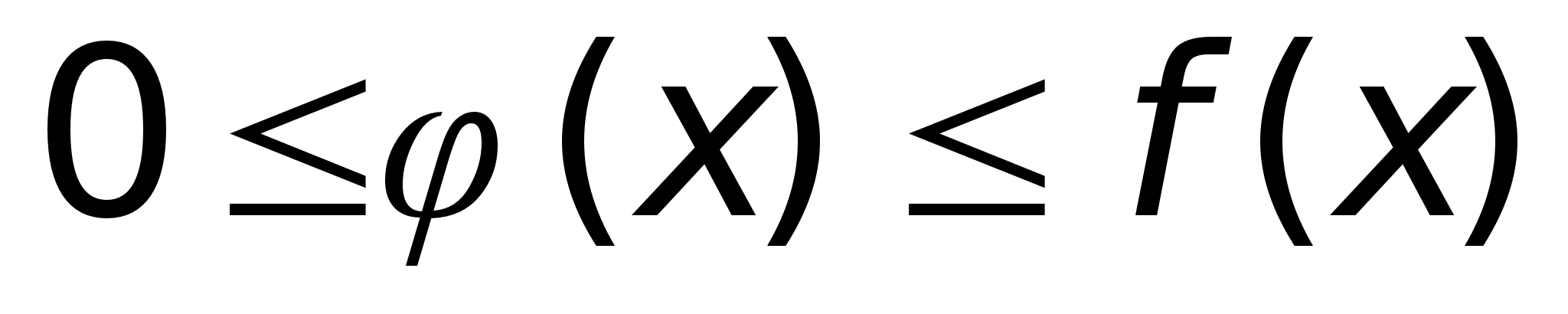 ,
то справедливо
следующее
утверждение:
,
то справедливо
следующее
утверждение:
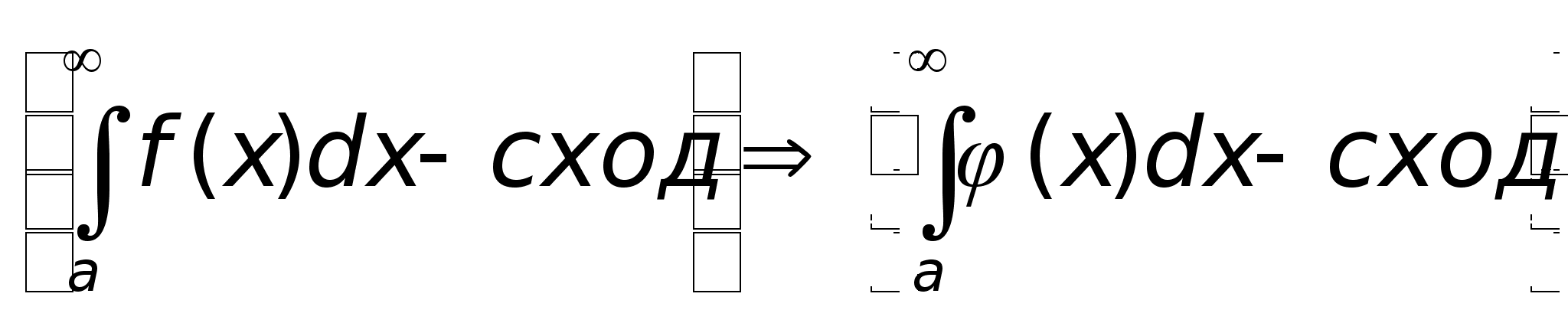
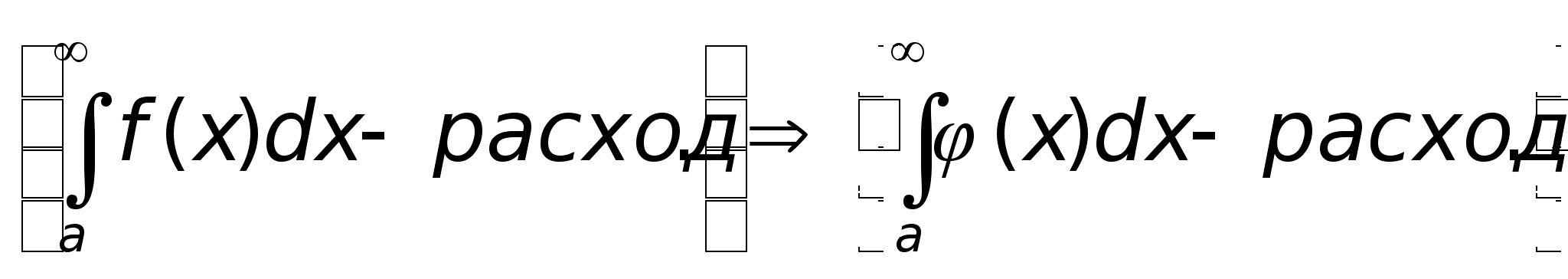
Обратное утверждение неверно!!!
Rn
*******
На арифм. эмерном пространстве метрика вводится по формуле:
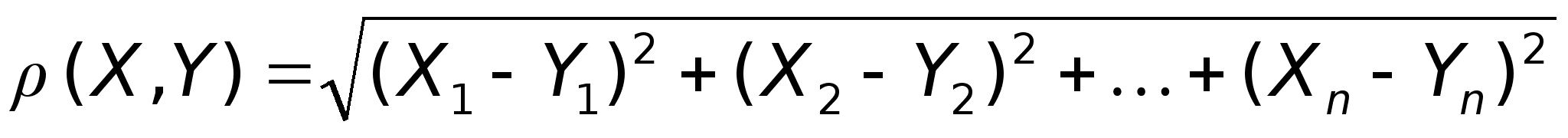 ,
где
,
где
Арифм. эмерное пространство, сведенное с метрикой по формуле - евклидово пространство.
Понятие окрестности в Rn
Интегрирование с помощью подстановки.
Пусть подынтегральная
ф-ия в интеграле
непрерывна
на Х
и ф-ия
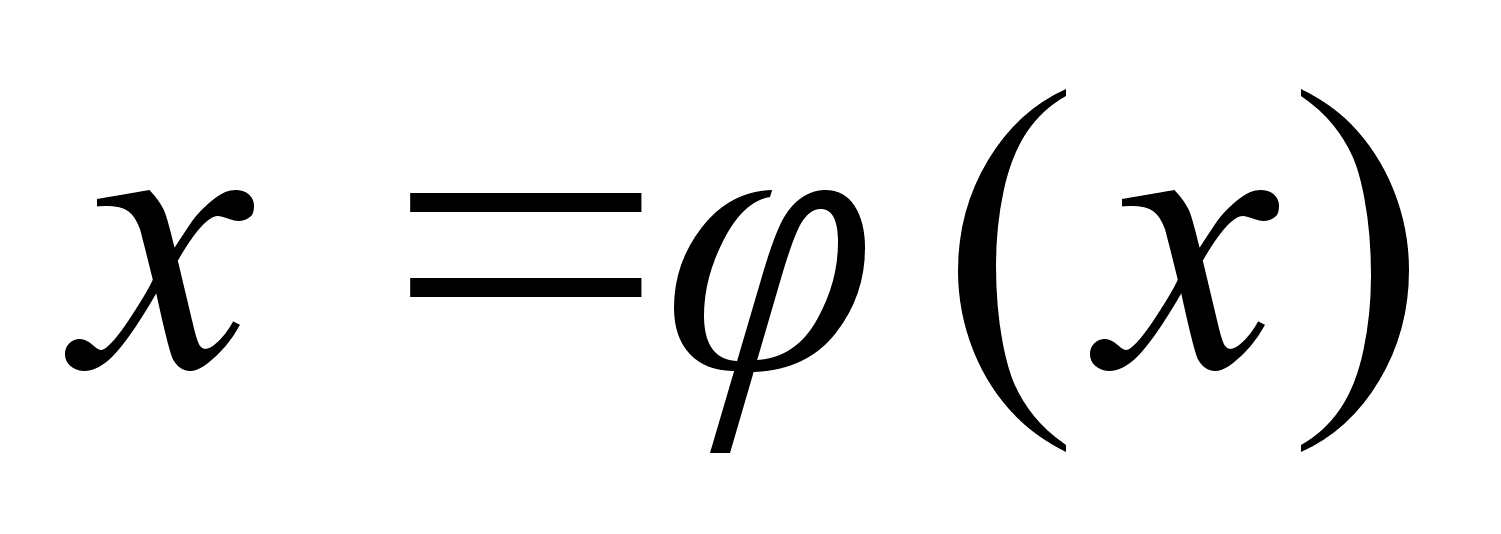 дифф. на промежутке
Т и имеет
на нем обратную
ф-ию
дифф. на промежутке
Т и имеет
на нем обратную
ф-ию
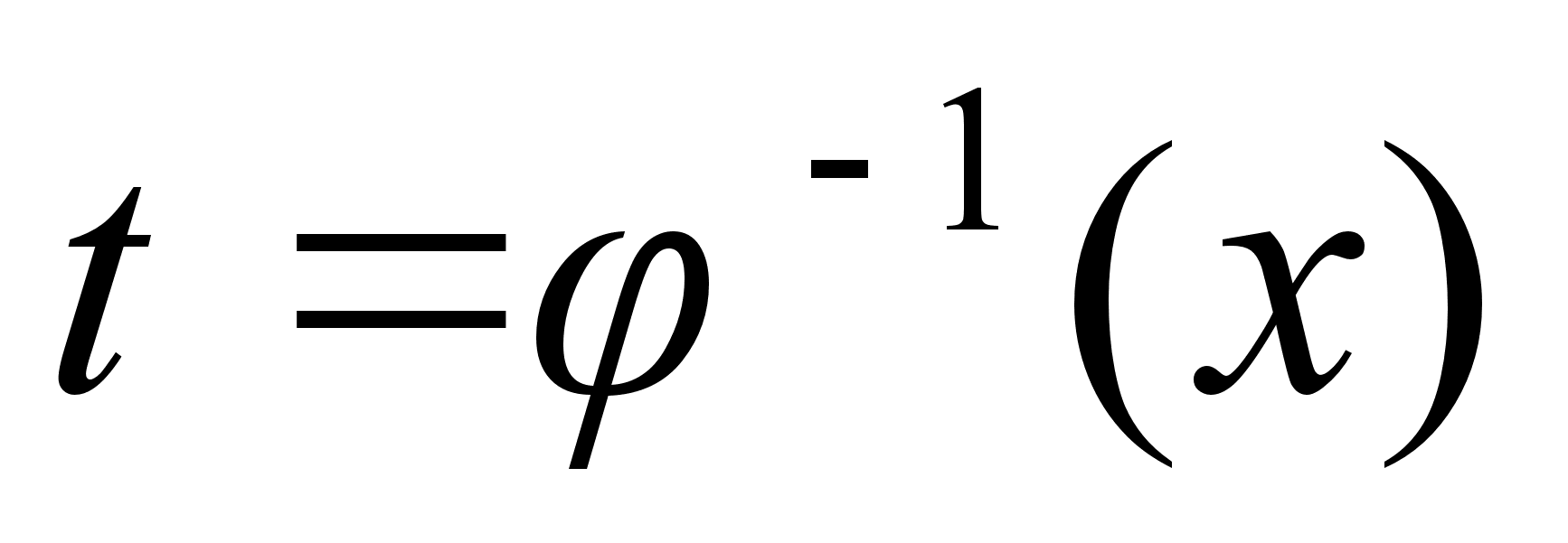 с
с
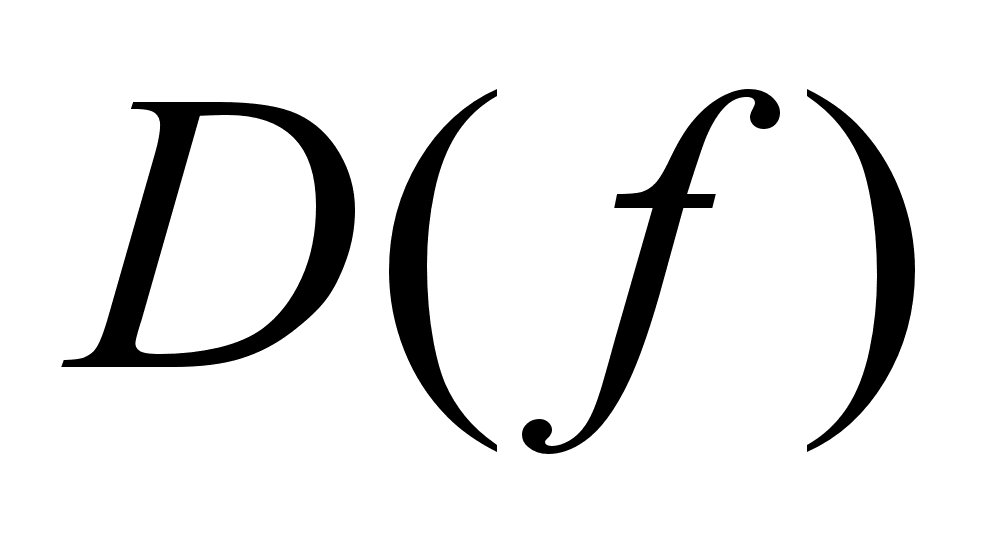 на
промежутке
Х , тогда
справедливо:
на
промежутке
Х , тогда
справедливо:
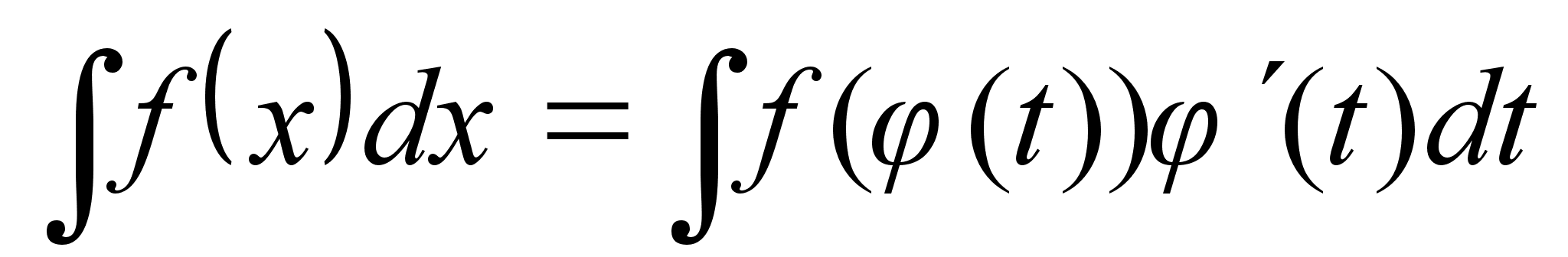
Алгоритм интегрирования подстановкой.
Для интеграла подынтегральная ф-ия
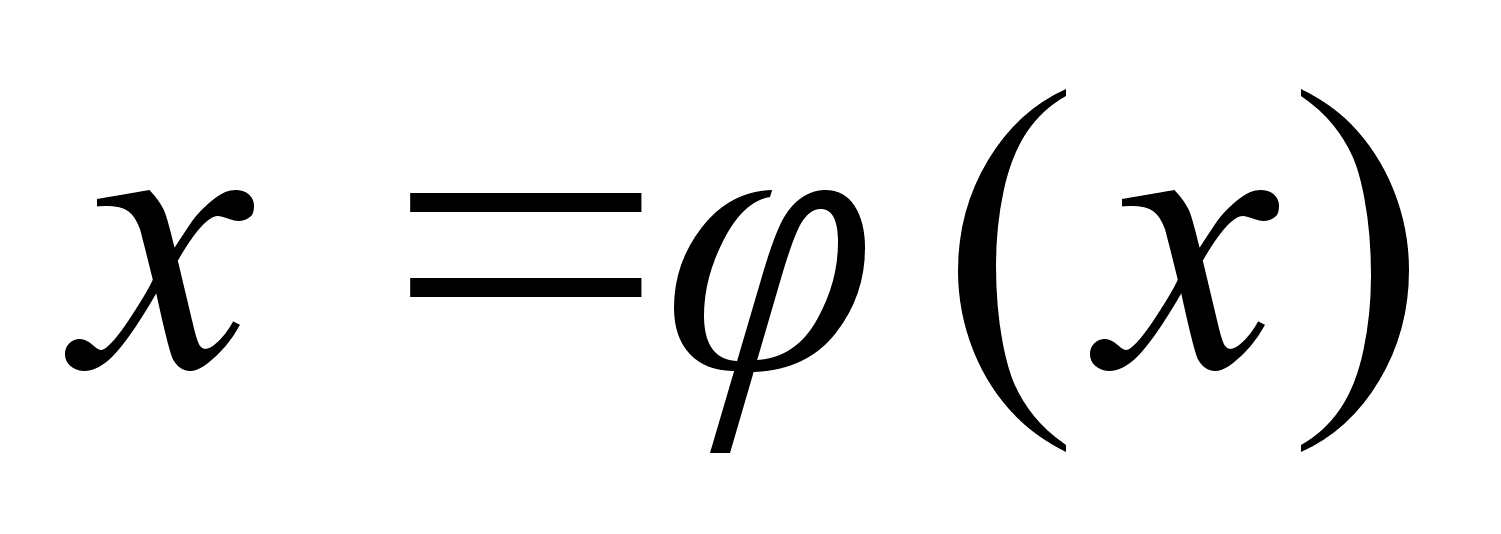 такая,
что
такая,
что
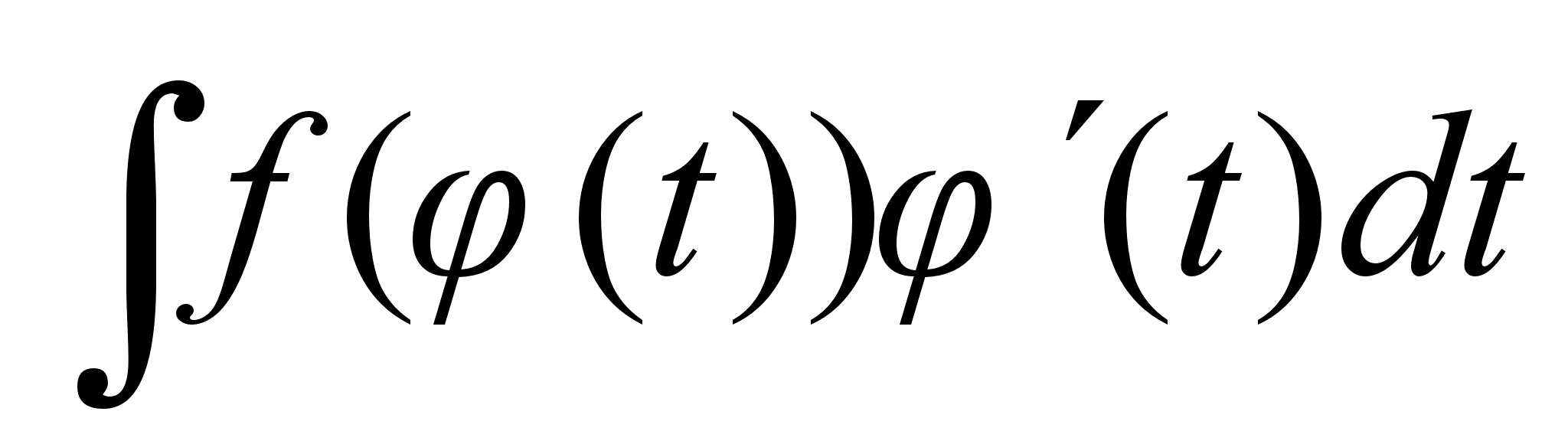 является табличным
или сводится
к нему так, что
легко находится
является табличным
или сводится
к нему так, что
легко находится
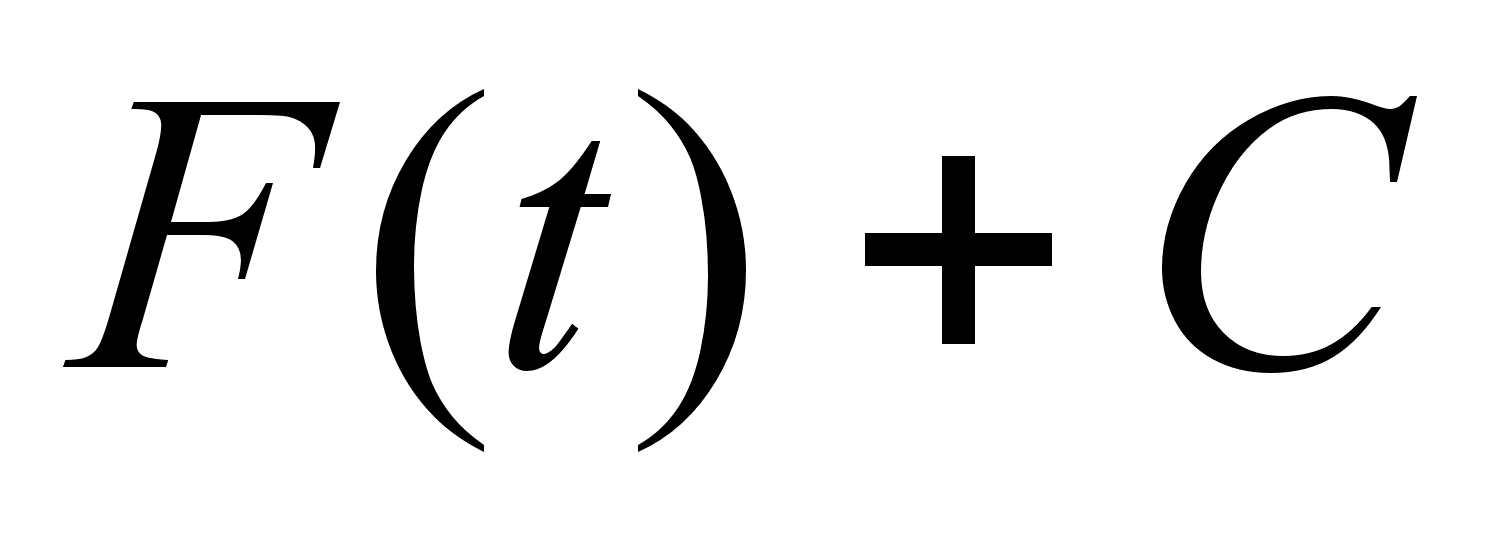 .
.Нах. обратную ф-ию
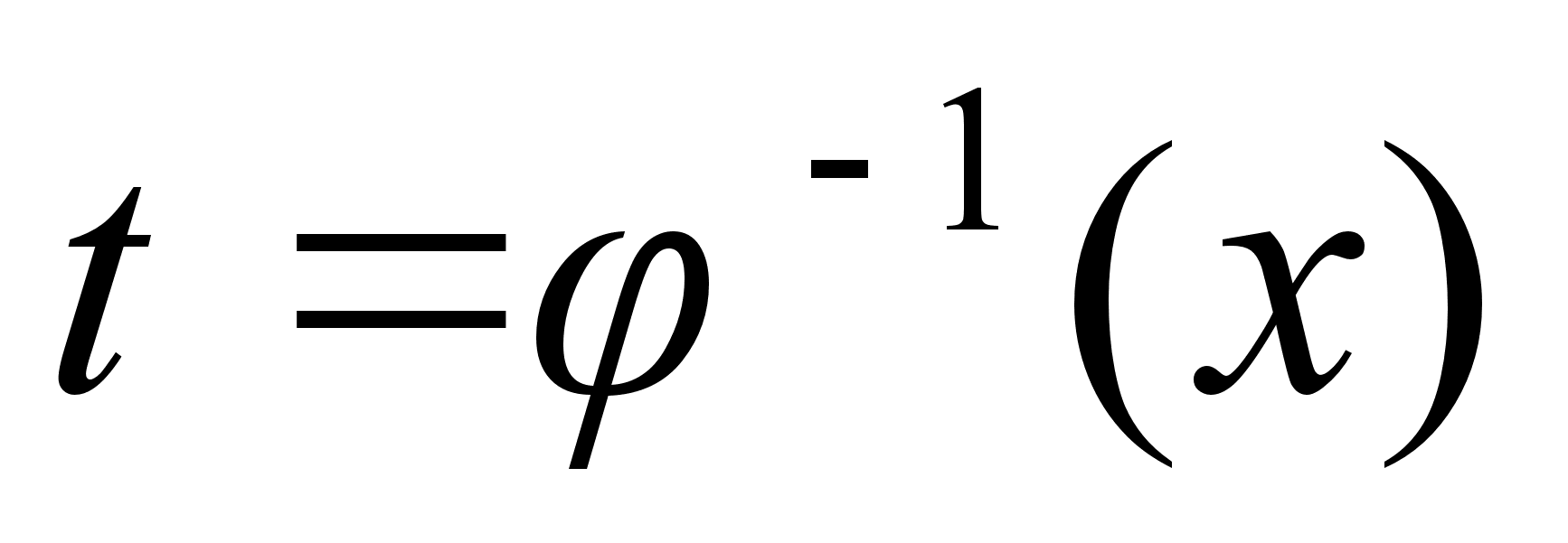 и подставляем
в
и подставляем
в
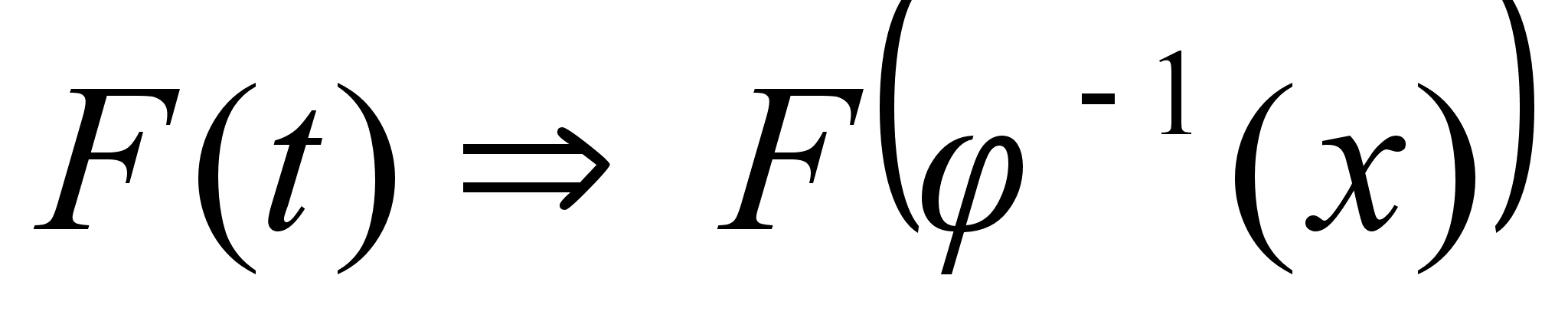 ,
которая и будет
первообразной
для исходного
интеграла.
,
которая и будет
первообразной
для исходного
интеграла.
Алгоритм:
Часть подынтегрального выражения вводится под знак дифференциала и полученное выражение под знаком дифференциала обозначается как новая переменная.
В подынтегральной ф-ии делается замена переменной на новую, находится
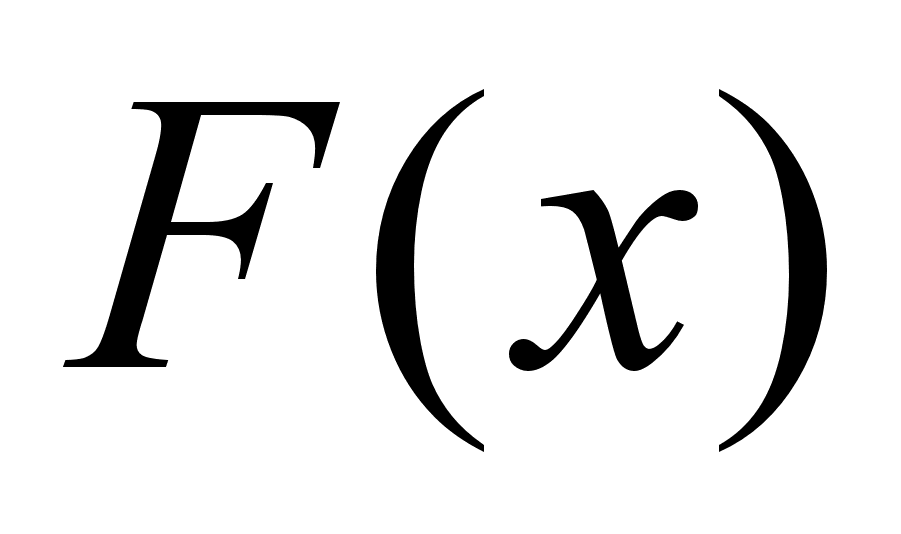 от новой переменной.
от новой переменной.В
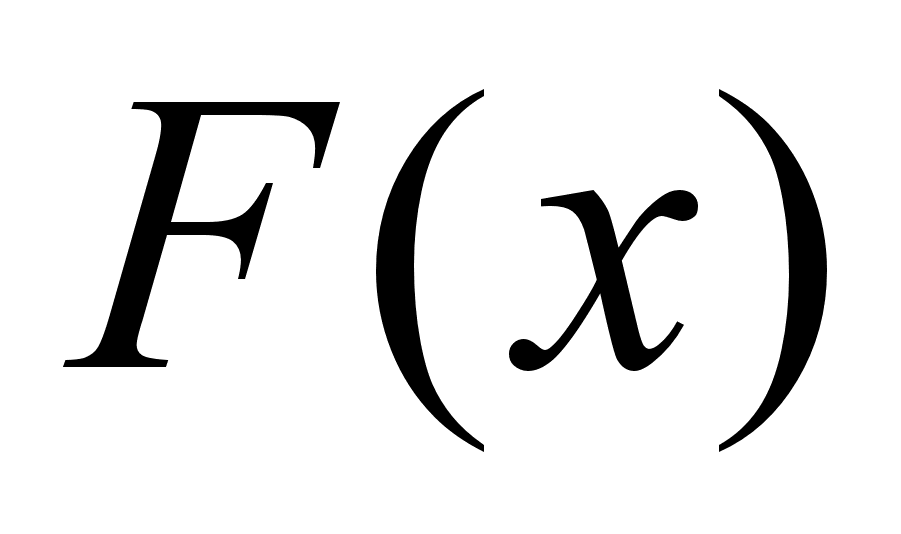 возвращ. к старой
переменной.
возвращ. к старой
переменной.
Интегрирование по частям.
Интегрирую выражение любого дифференциала произведения, получим:
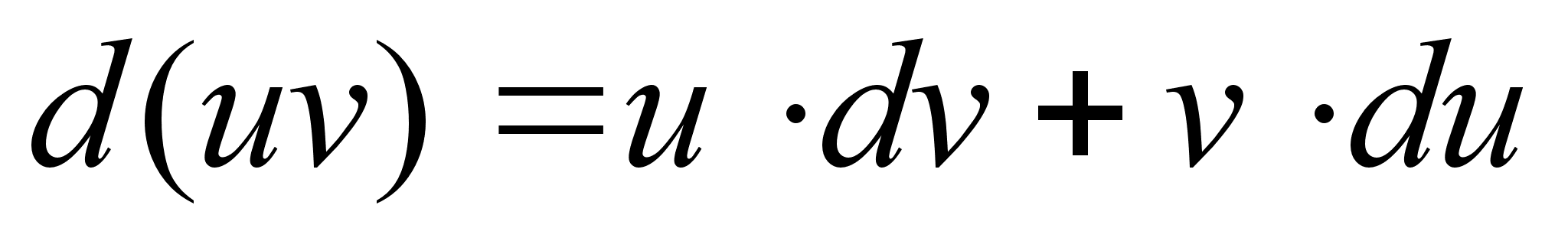
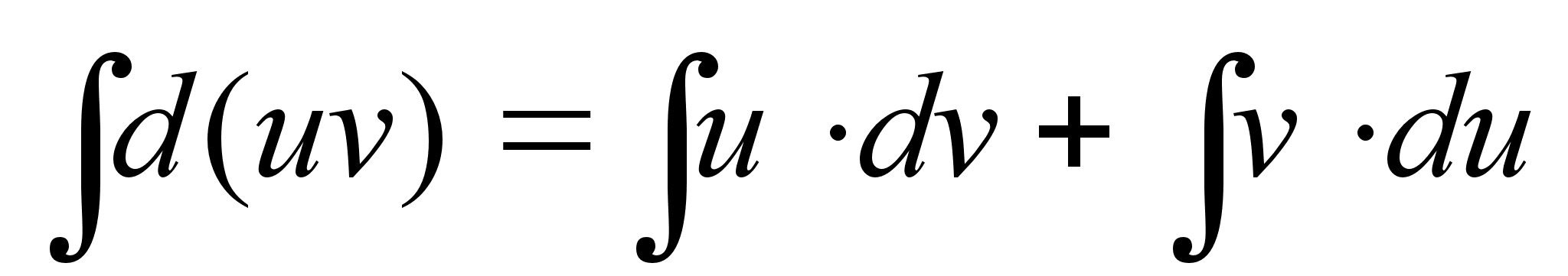
Пример:
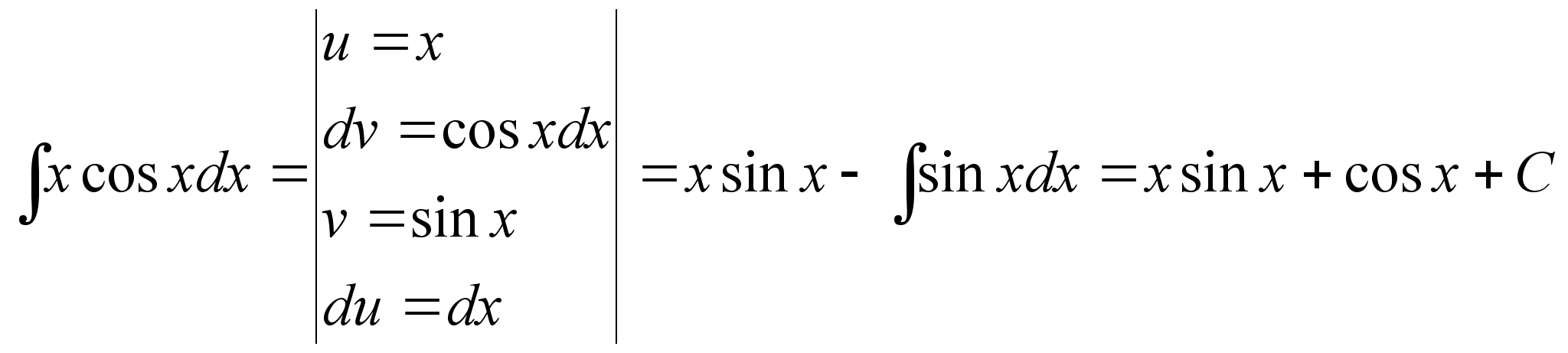
Рекомендации:
В интегралах с подынтегральным выражением вида:
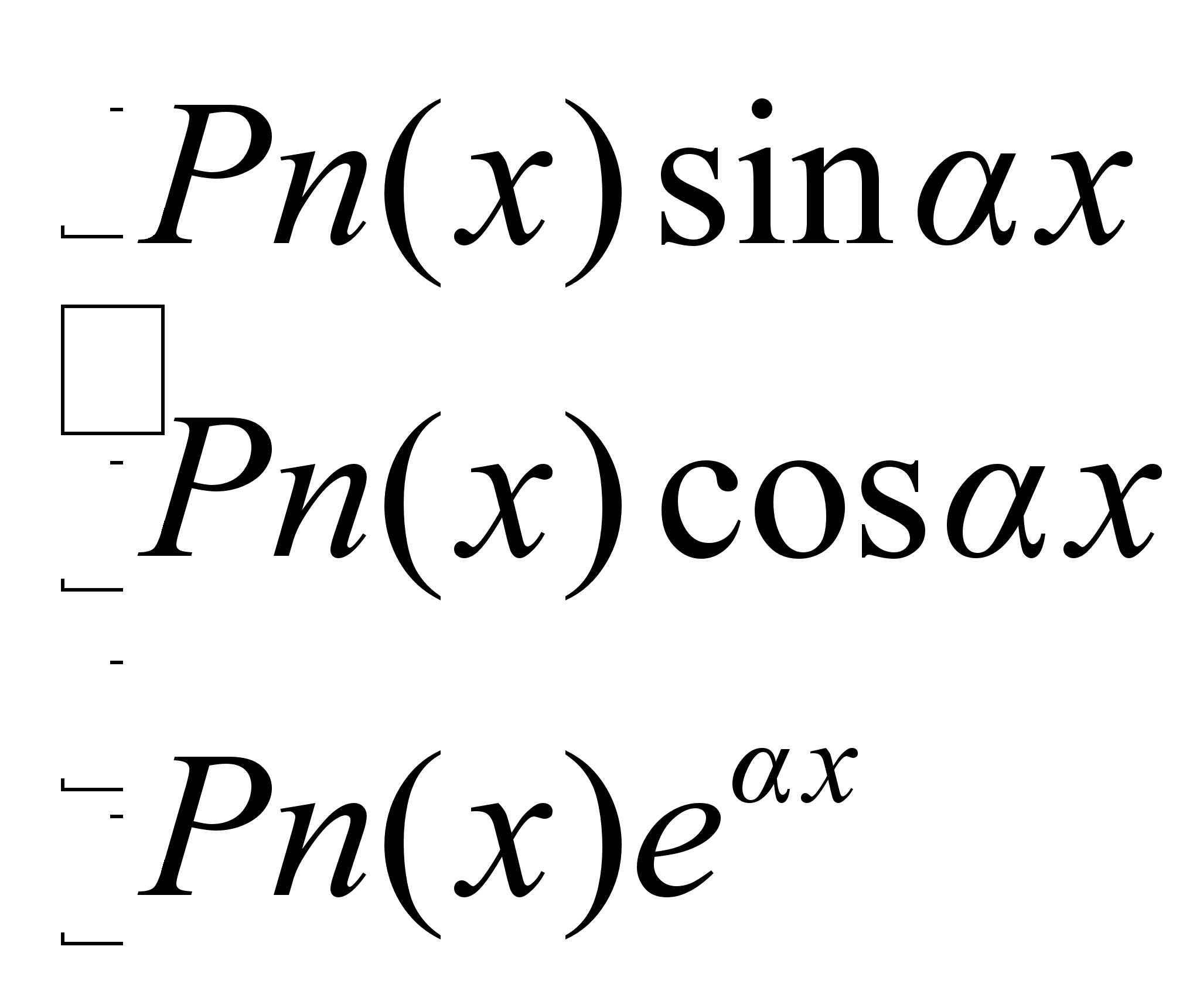 (Pn
–многочлен
степени n
)
(Pn
–многочлен
степени n
)
Pn принимается за u
В интегралах с подынтегральным выражением вида:
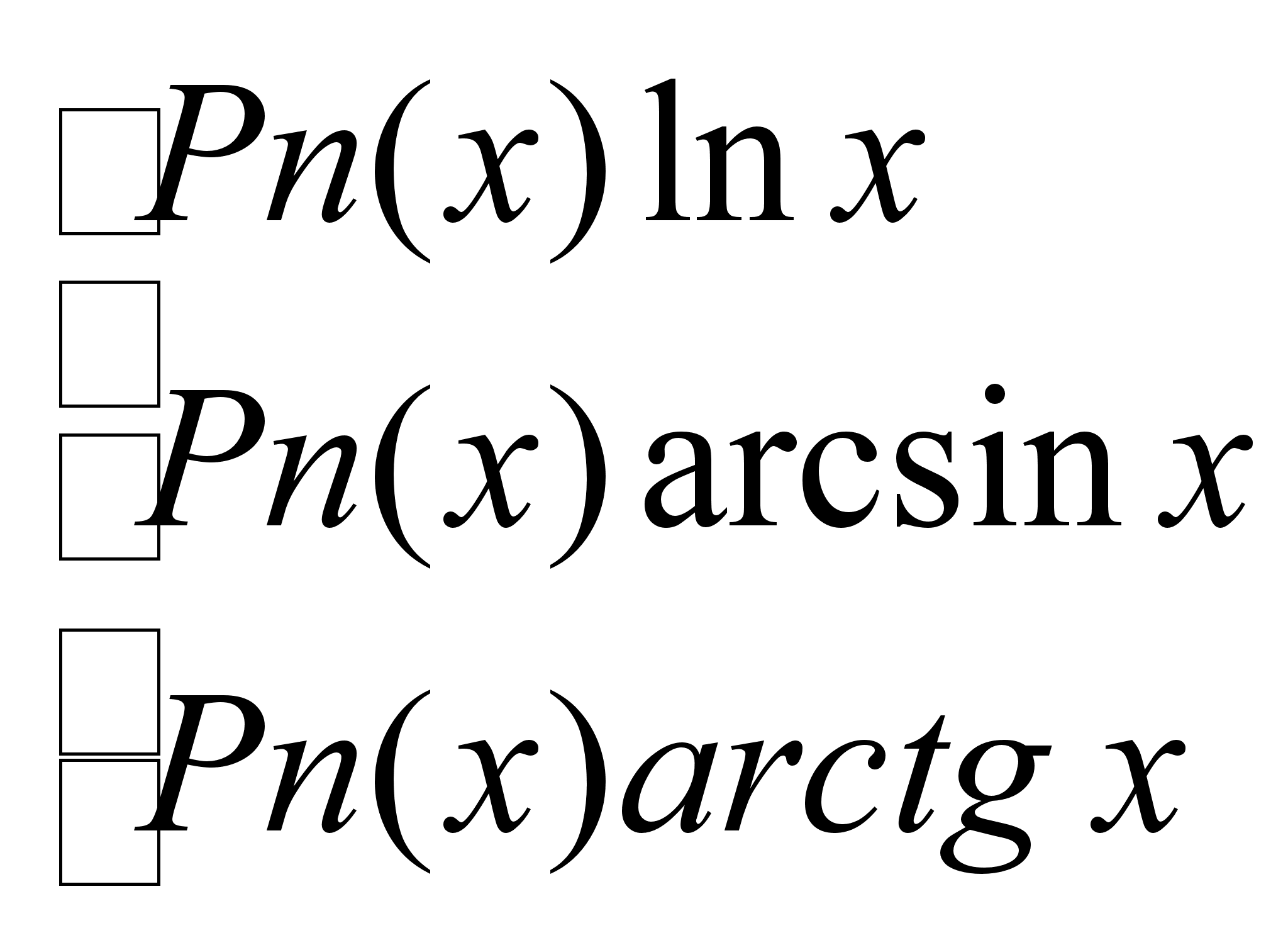
за u
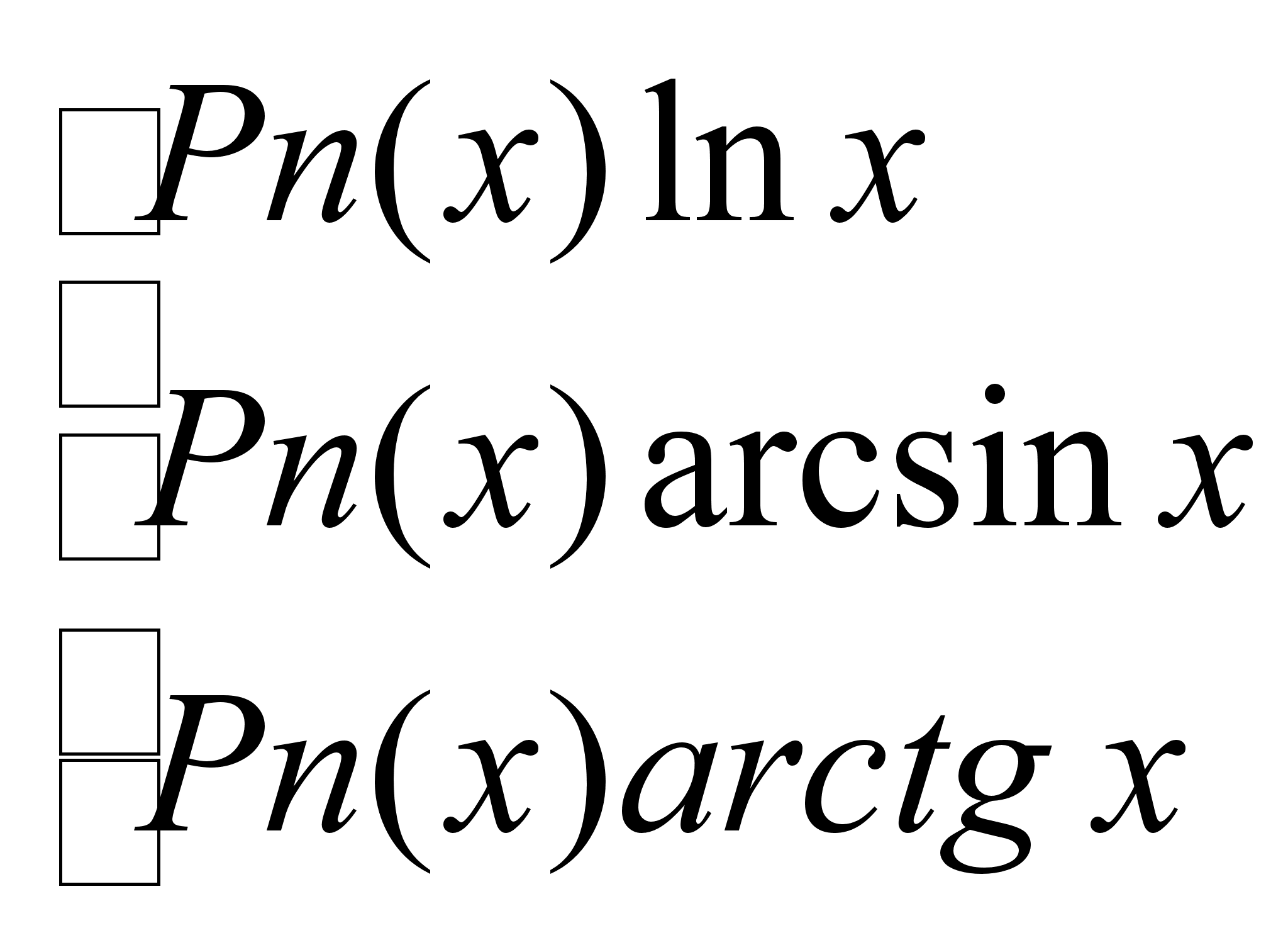
Интегрирование
с подстановкой
выражений вида
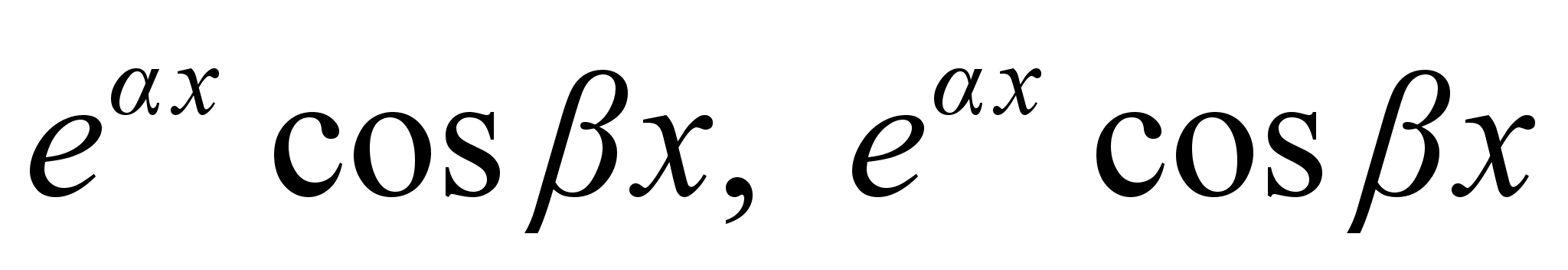 после двукратного
интегрирования
по частям приводится
к линейному
уравнению
относительно
вычисляемого
интеграла.
после двукратного
интегрирования
по частям приводится
к линейному
уравнению
относительно
вычисляемого
интеграла.
Интегрирование дробно-рациональных выражений
Df Дробно-рациональная
ф-ия
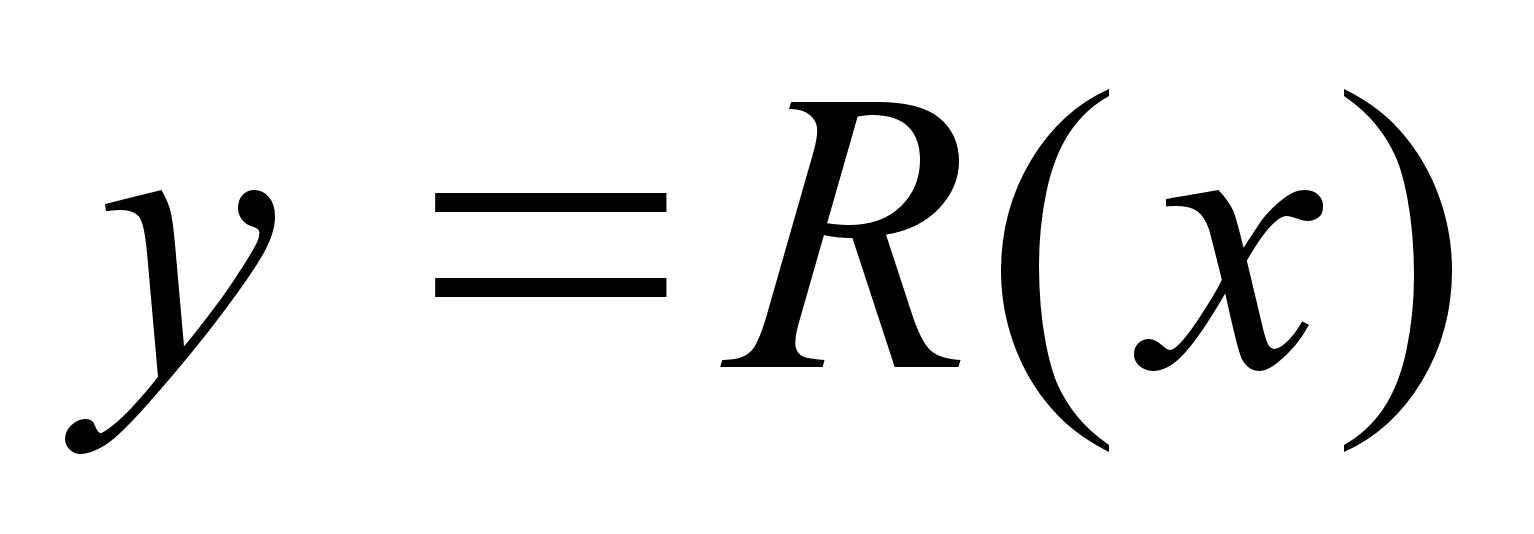 -
отношение 2х
многочленов
-
отношение 2х
многочленов
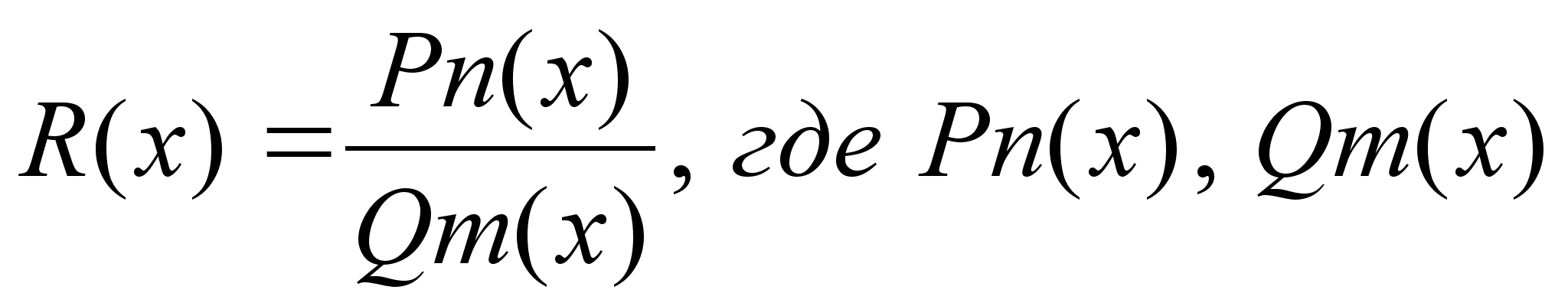 -
многочлены
степени n
и m
соответственно.
-
многочлены
степени n
и m
соответственно.
Рациональная дробь правильная, если степень числителя строго меньше степени знаменателя, обратно - неправильная.
Zm Неправильная рациональная дробь путем выделения целой части приводится к сумме многочлена и правильной рациональной дроби; многочлен называется целой частью неправильной дроби.
Простейшие (элементарные) рациональные дроби и их применение.
К простым рациональным дробям относятся рациональные дроби типов:
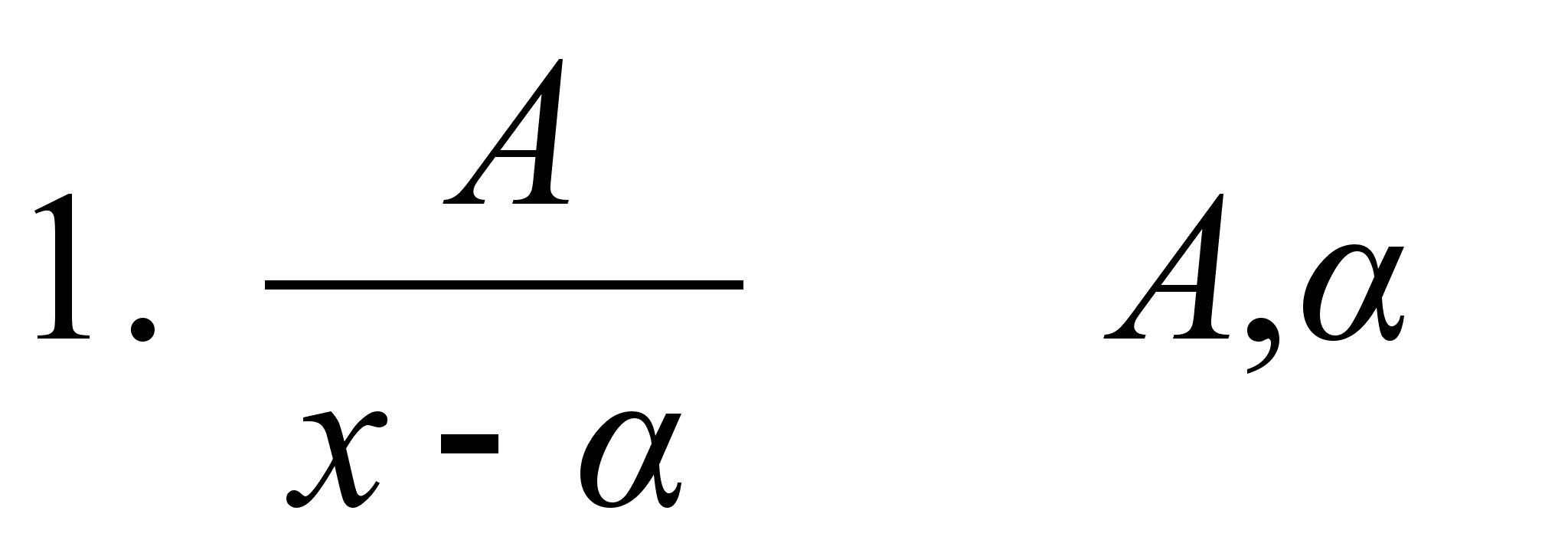 -
вещественные
постоянные
-
вещественные
постоянные
2.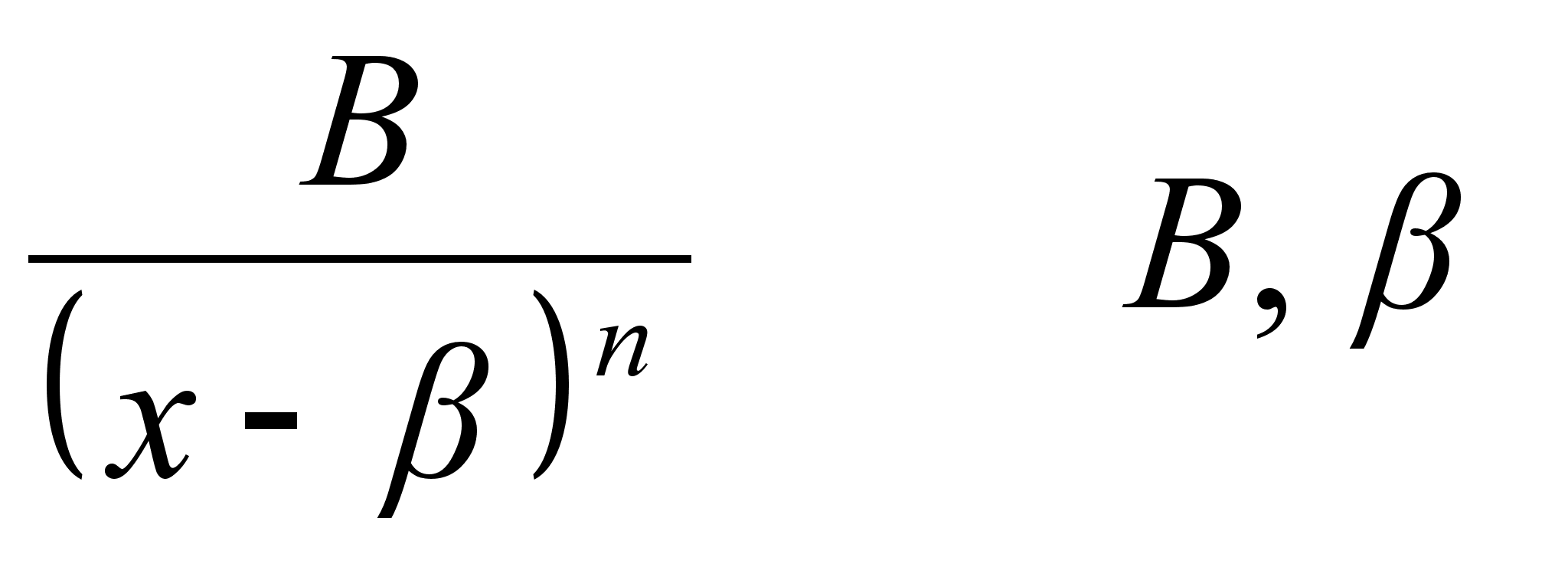 -
вещественные
постоянные,
-
вещественные
постоянные,
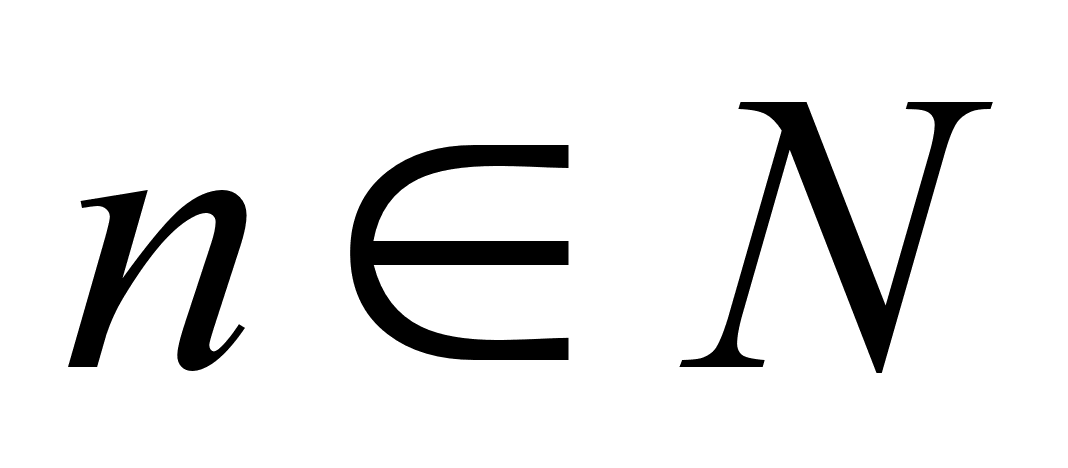
3.
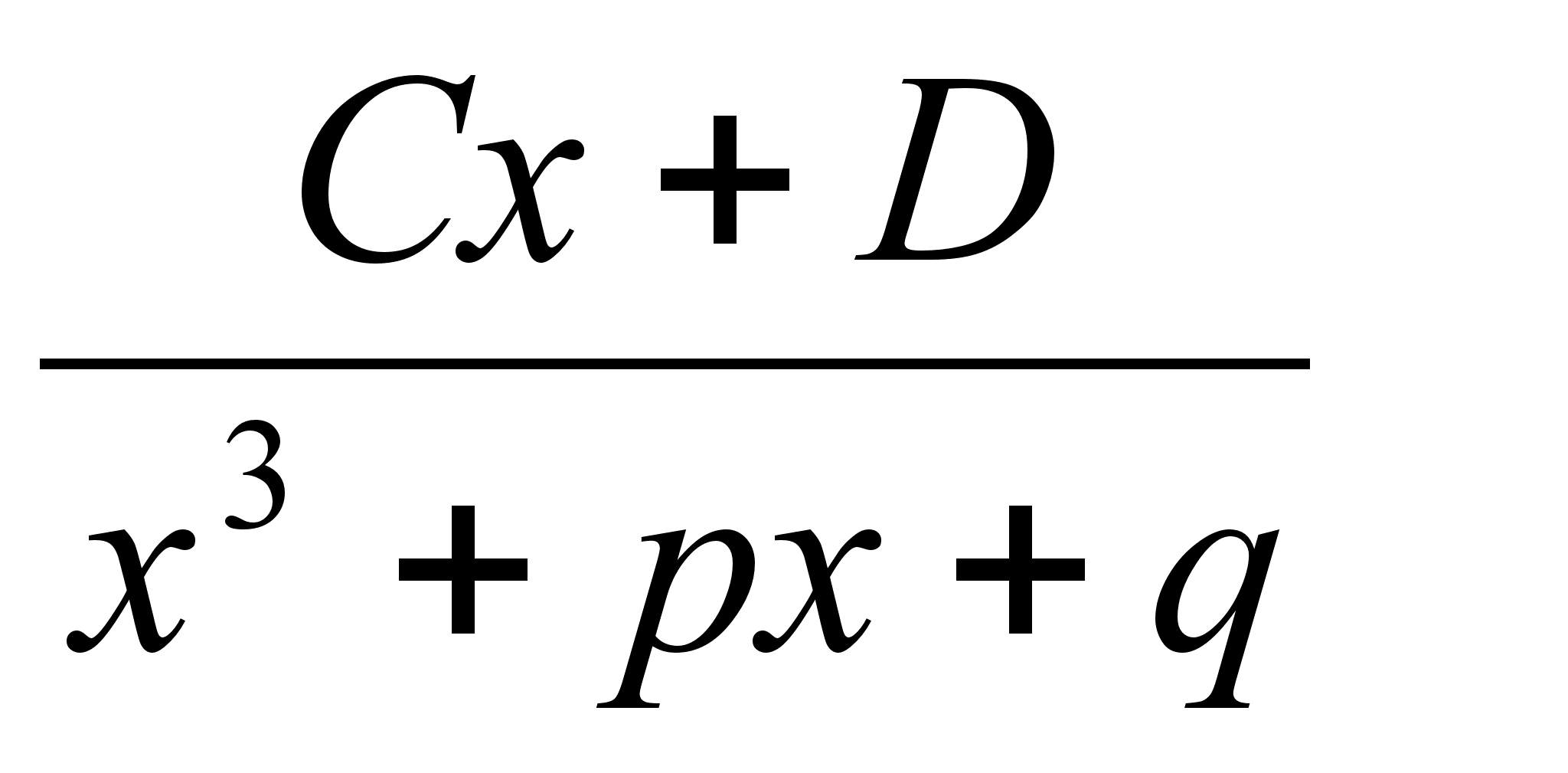
4.
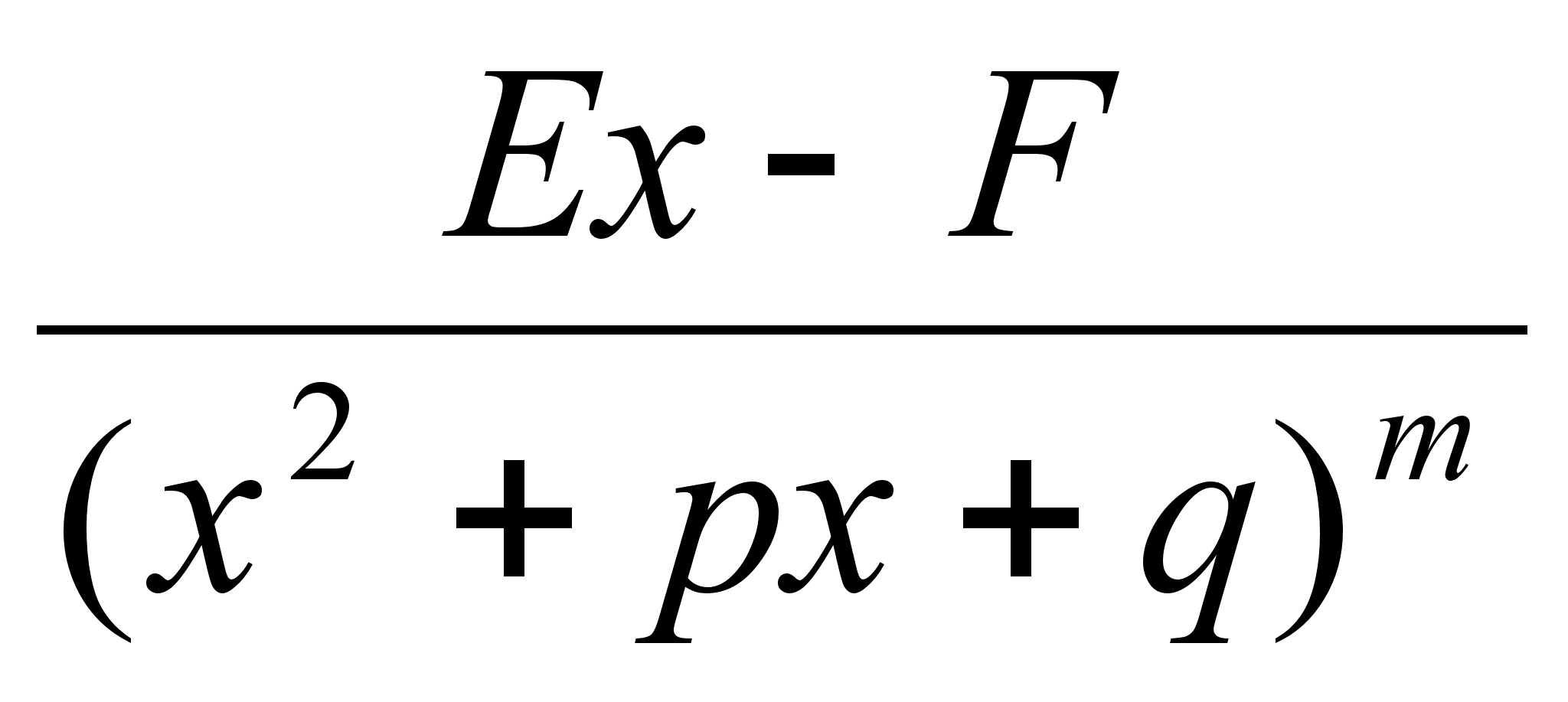
Интегрирование 1го типа:

Интегрирование 2го типа:
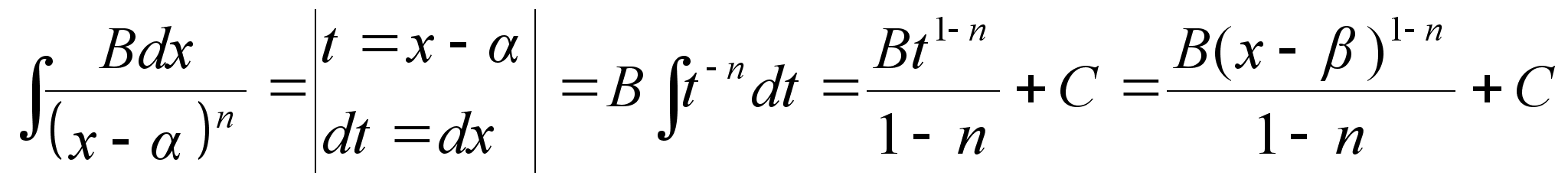
Интегрирование 3го типа:
проводится в два этапа:
1. В числителе выделяется дифференциал знаменателя:
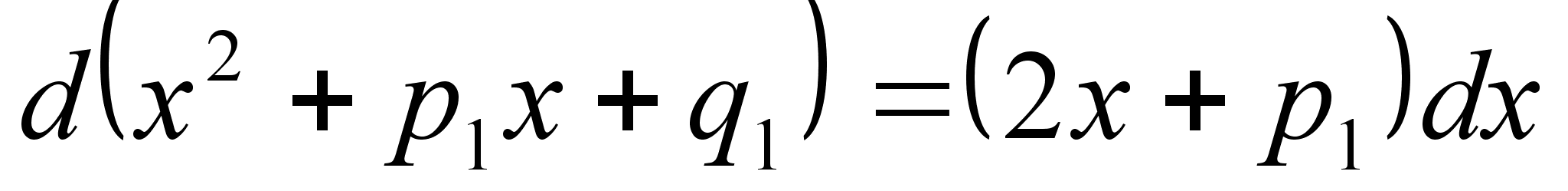
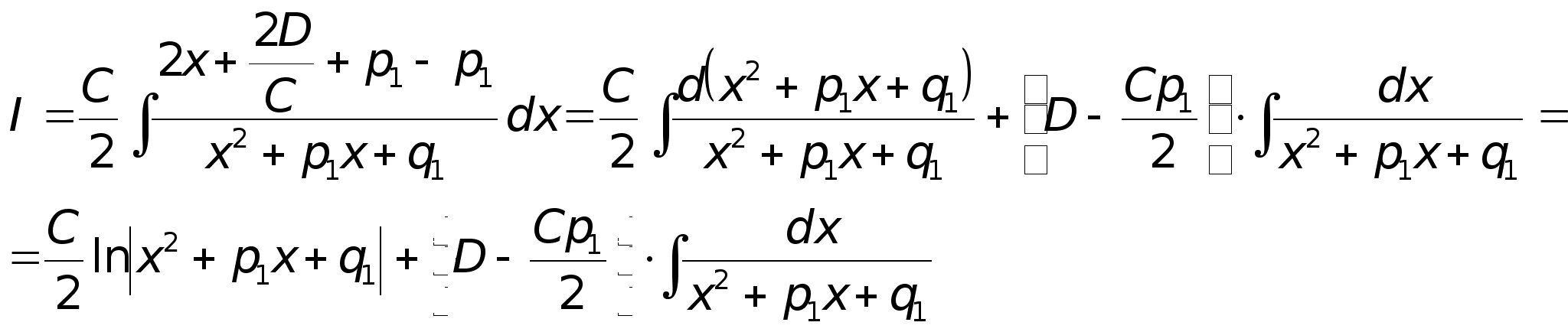
2. Выделение полного квадрата в знаменателе второго интеграла.
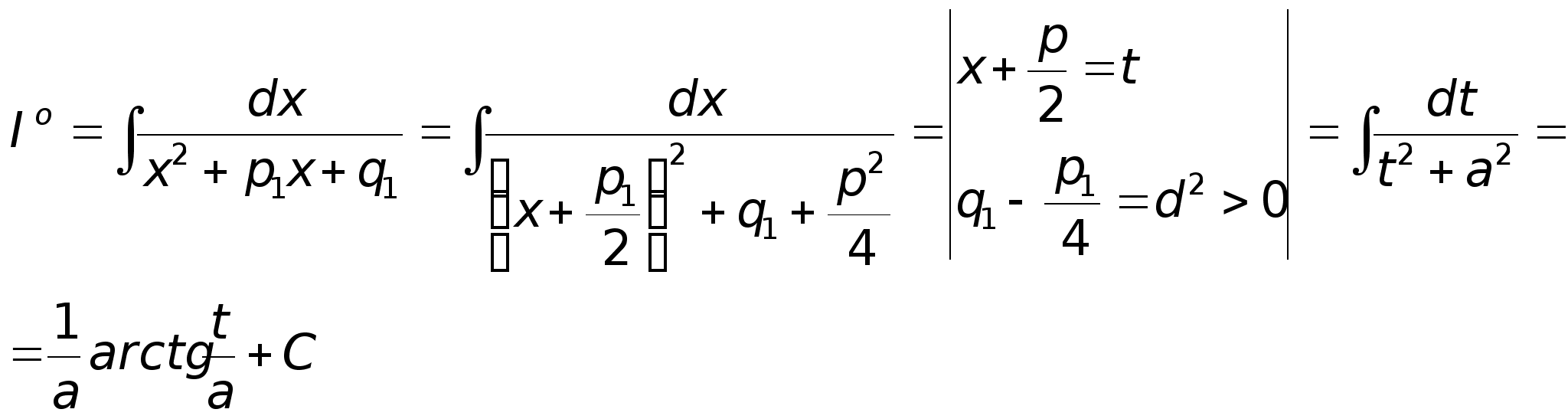
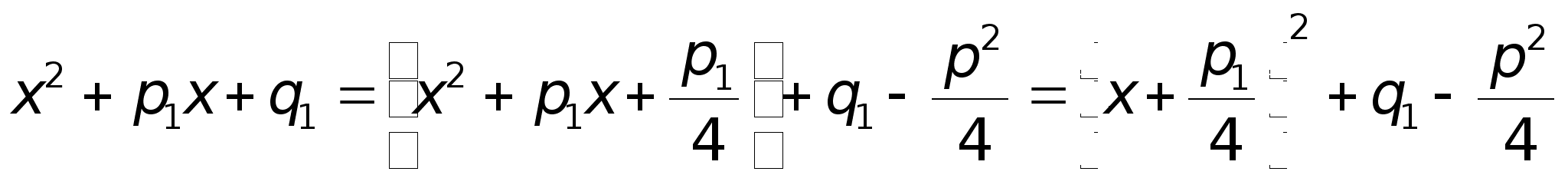
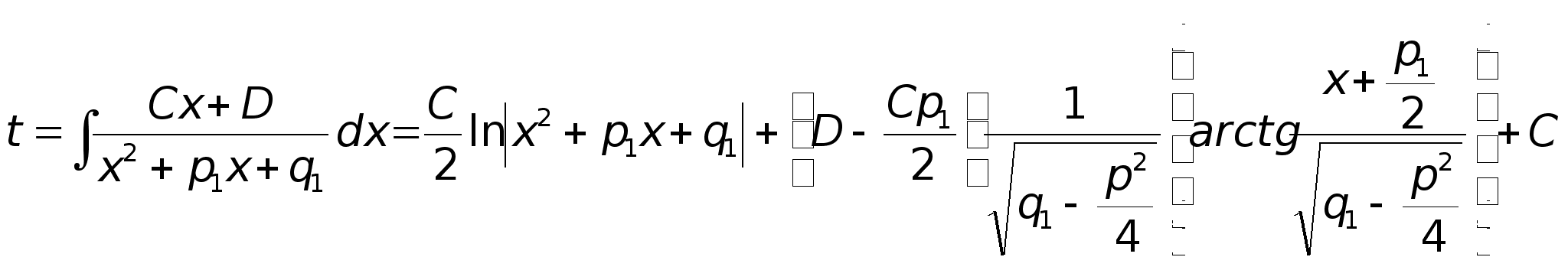
Интегрирование 4го типа:
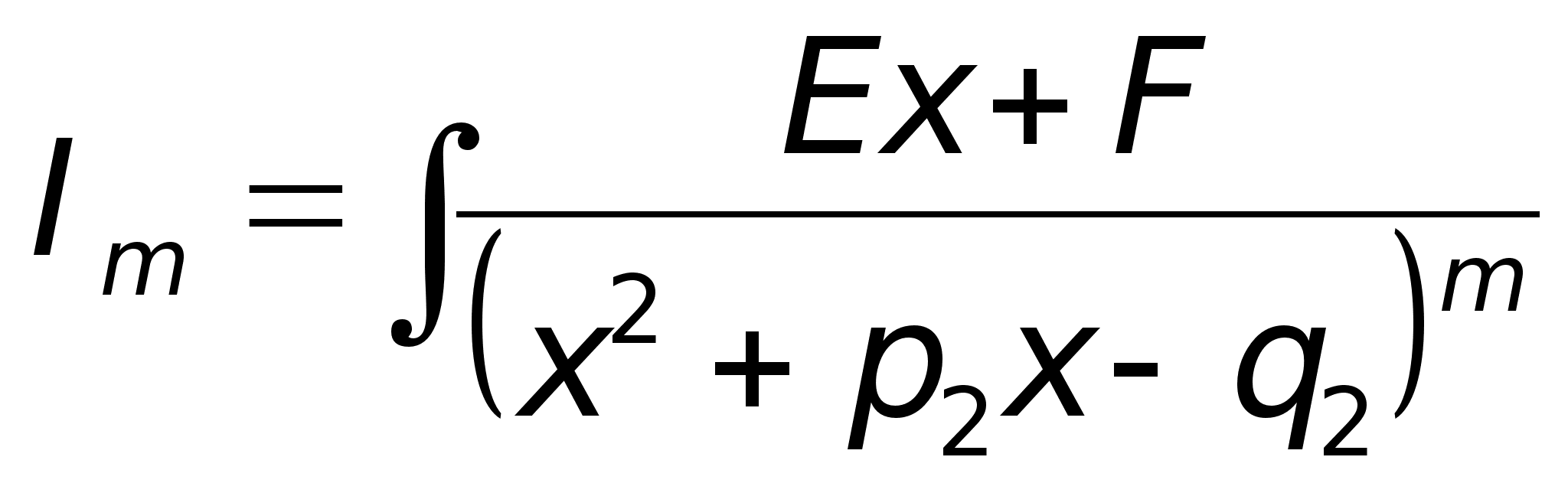
1. Выделяем в числителе *** знаменателя:
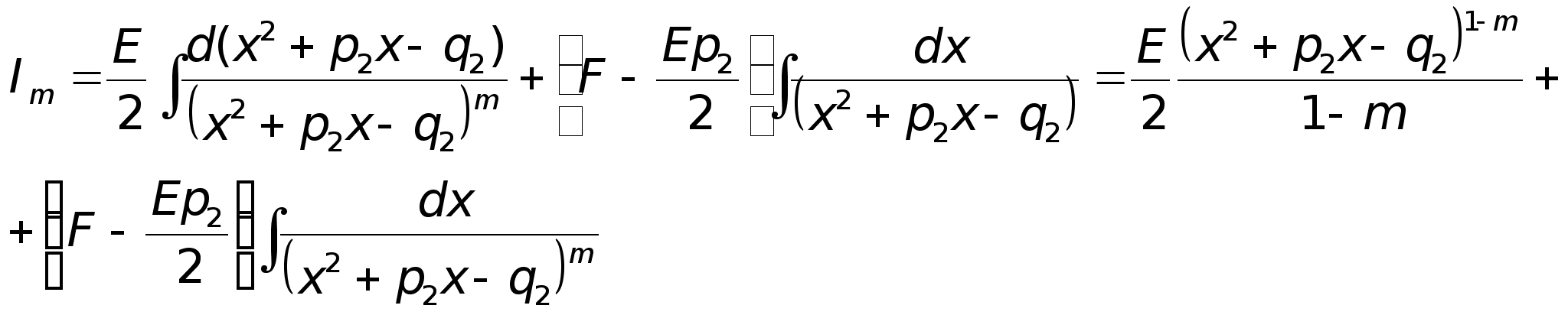
Выделяем в знаменателе 2го интеграла ф-лы квадрата:
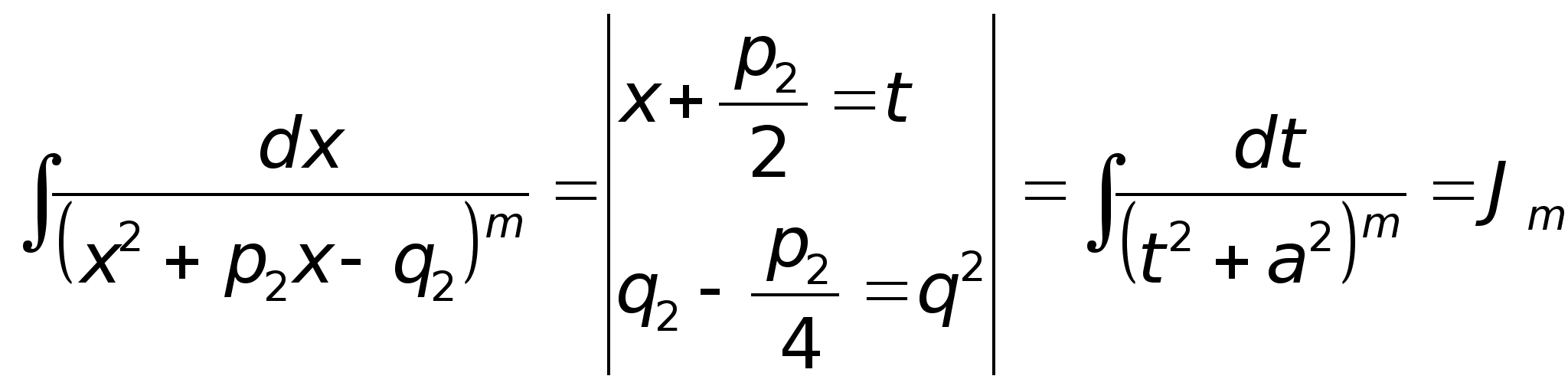
Рекуррентная формула для вычисления Jm (вычисление происходит путем подстановки в известную форму)
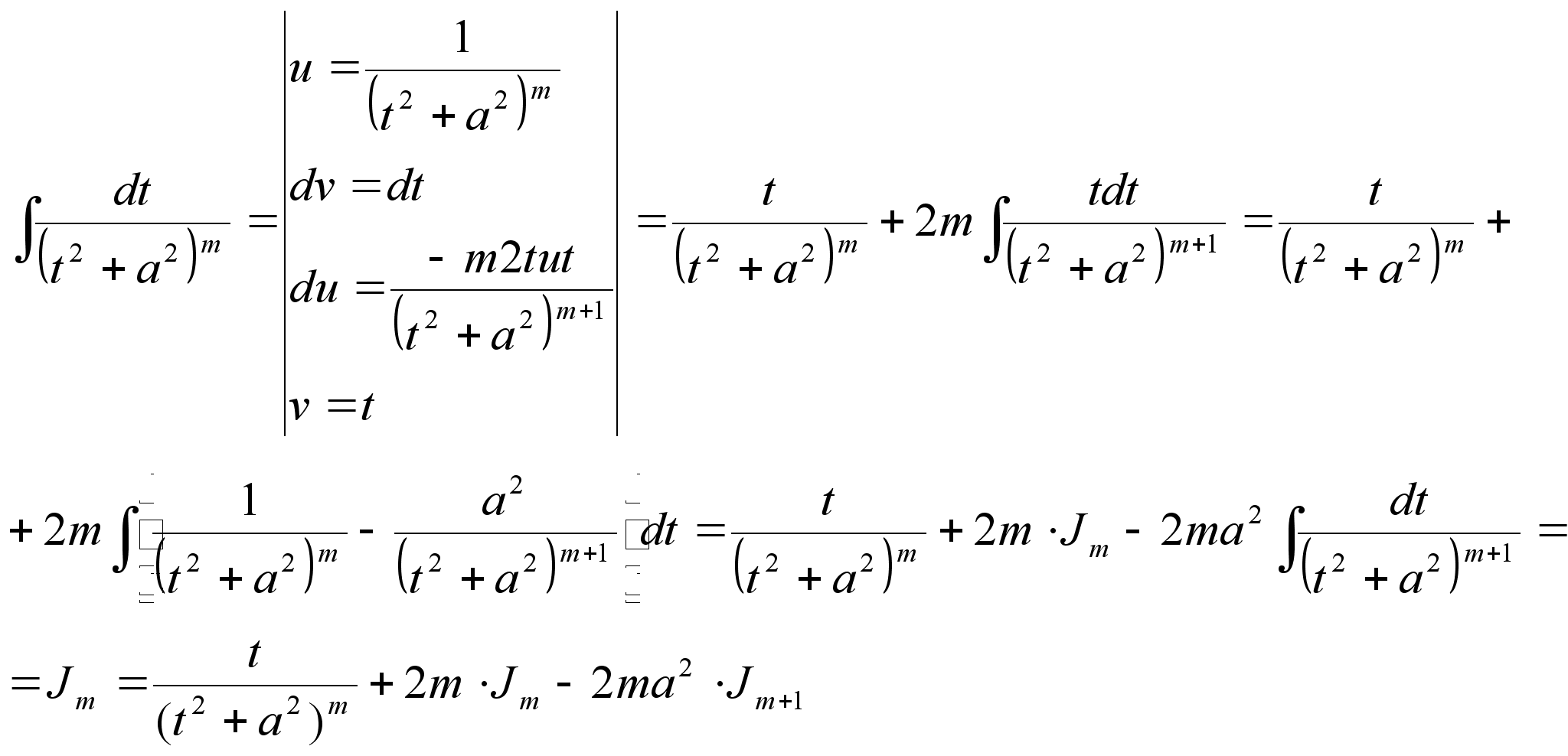
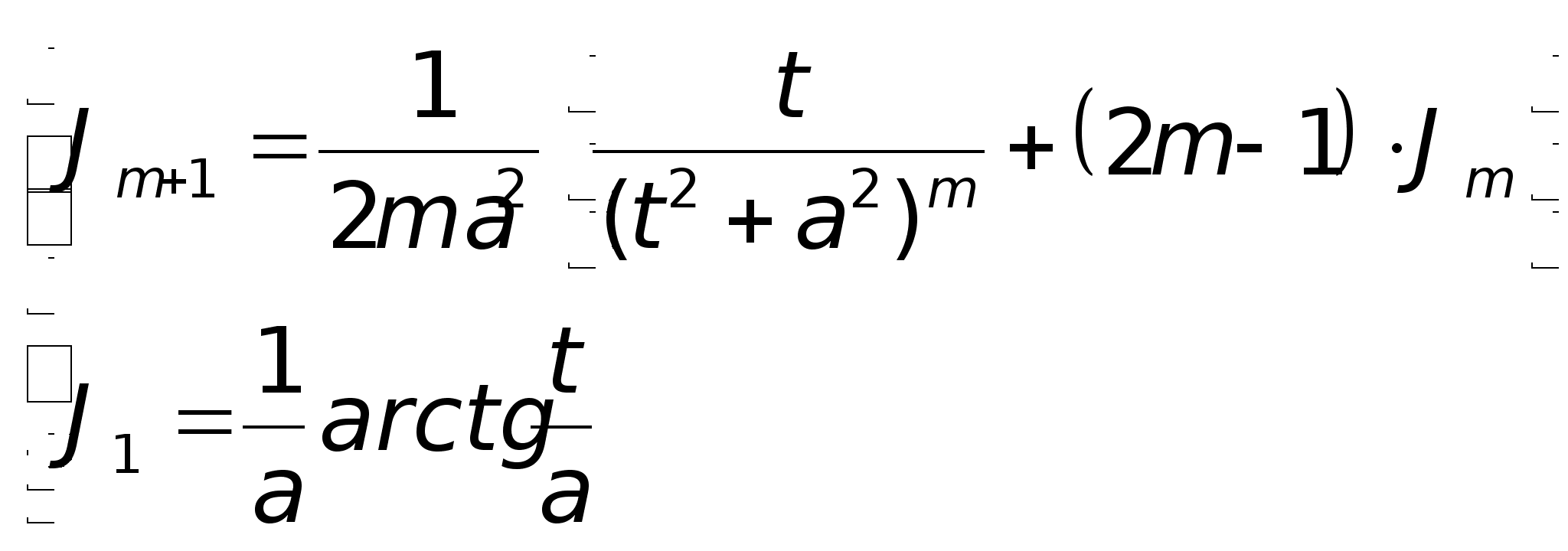
Разложение рациональной дроби на простейшие.
В курсе алгебры доказываются утверждения