Математические модели в естествознании
модели в естествознании" width="46" height="42" />генотипов A и a (они же -частоты гамет) совпадают с частотами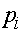 и
и 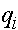 женских гамет в i -ом поколении. В силу данного обстоятельства и формул (9), (10) получаем следующие уравнения для эволюции частот женских и мужских гамет:
женских гамет в i -ом поколении. В силу данного обстоятельства и формул (9), (10) получаем следующие уравнения для эволюции частот женских и мужских гамет:
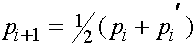 ,
, 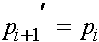 , (11)
, (11)
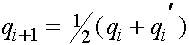 ,
, 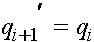 . (12)
. (12)
Решим систему разностных уравнений (11) описанным выше способом. Выпишем матрицу правых частей:
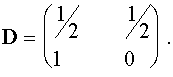
Ее собственные значения определяются из характеристического уравнения
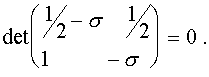
Раскрывая определитель, получаем
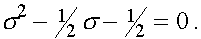
Находим корни: 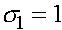 и
и 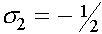 . Собственные векторы
. Собственные векторы  ,
, 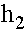 - нетривиальные решения систем:
- нетривиальные решения систем:
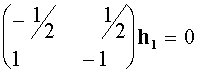 ,
, 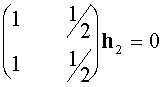 ,
,
из которых следует, что
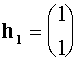 ,
, 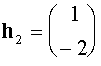 .
.
Система разностных уравнений (11) имеет частные решения 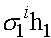 и
и 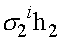 . Общим решением системы является их линейная комбинация:
. Общим решением системы является их линейная комбинация:
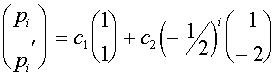 .
.
Из начального условия
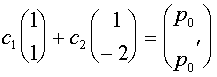
определяем константы 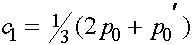 и
и 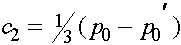 . В результате получаем явную зависимость частот женских и мужских гамет A от номера поколения:
. В результате получаем явную зависимость частот женских и мужских гамет A от номера поколения:
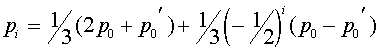 ,
,
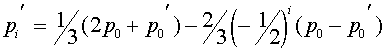 .
.
Совершенно аналогично из (12) для частот женских и мужских гамет a получаем:
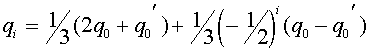 ,
,
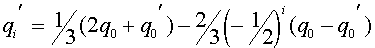 .
.
Используя полученные формулы для эволюции частот, сделаем ряд выводов. Положим: 
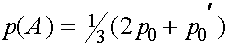 ,
, 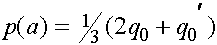 . Отметим, что
. Отметим, что 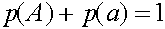 . С ростом номера поколения частоты женских и мужских гамет A стремятся к общему пределу
. С ростом номера поколения частоты женских и мужских гамет A стремятся к общему пределу 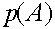 , соответственно частоты гамет a стремятся к пределу
, соответственно частоты гамет a стремятся к пределу 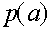 . Последовательности частот сходятся немонотонно, но со скоростью геометрической прогрессии, т.е. весьма быстро. Напомним, что в i -ом поколении частоты женских генотипов AA, Aa, aa суть
. Последовательности частот сходятся немонотонно, но со скоростью геометрической прогрессии, т.е. весьма быстро. Напомним, что в i -ом поколении частоты женских генотипов AA, Aa, aa суть 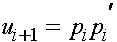 ,
, 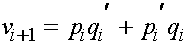 ,
, 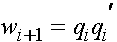 .
.
Отсюда следует, что в пределе
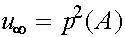 ,
, 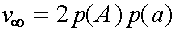 ,
, 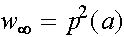 .
.
Таким образом, для женских генотипов в пределе имеет место закон Харди -Вайнберга. Так как сходимость к пределу очень быстрая, то на практике можно считать, что после смены трех -четырех поколений частоты женских генотипов AA, Aa, aa суть 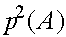 ,
, 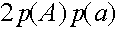 ,
, 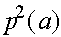 . Аналогично, частоты мужских генотипов A и a после смены нескольких поколений приближенно равны
. Аналогично, частоты мужских генотипов A и a после смены нескольких поколений приближенно равны 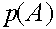 и
и 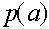 .
.
Напомним, что гены дальтонизма и гемофилии являются рецессивными. Согласно полученным результатам, сцепленный с полом дефект, который встречается у мужчин с вероятностью 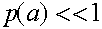 , у женщин проявляется с гораздо меньшей вероятностью
, у женщин проявляется с гораздо меньшей вероятностью 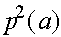 .
.
Закон Харди -Вайнберга гласит, что при отсутствии возмущений частоты аллелей не изменяются. Однако процессы, изменяющие частоты генов, постоянно происходят в популяции. Без них не было бы эволюции. Рассмотрим процессы отбора. К идее естественного отбора как основного процесса в эволюции пришли независимо друг от друга Чарльз Дарвин и Альфред Рассел Уоллес. В 1858 г. на заседании Линнеевского общества в Лондоне были представлены сообщения об их открытии. Доказательства того, что эволюция происходит путем естественного отбора были даны Ч. Дарвином в его работе "Происхождение видов" в 1859 г. Ч. Дарвин предположил, что в результате изменений появляются наследуемые признаки, которые обеспечивают их обладателям лучшую приспособленность к условиям среды. Такие организмы имеют больше шансов к выживанию и оставляют больше потомства, чем особи наделенные менее полезными свойствами. В результате частота признаков, обеспечивающих лучшую приспособленность (адаптивность), будет увеличиваться от поколения к поколению за счет частоты признаков, дающих меньшую адаптивность. Этот процесс был назван естественным отбором.
Рассмотрим простейший случай - модель отбора в двухаллельной менделевской популяции. В ее основе лежит закон Харди -Вайнберга расчета частот аллелей и генотипов. Припишем генотипам AA, Aa, aa числа 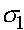 ,
, 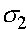 ,
, 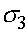 , которые назовем относительными приспособленностями. Данные коэффициенты можно интерпретировать как вероятности того, что особь соответствующего генотипа доживает до этапа размножения. Обозначим через
, которые назовем относительными приспособленностями. Данные коэффициенты можно интерпретировать как вероятности того, что особь соответствующего генотипа доживает до этапа размножения. Обозначим через 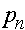 и
и 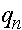 частоты
частоты 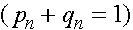 аллелей A и a в n -ом поколении в момент его появления (они же - частоты гамет n-1 ого поколения). Первоначально для n -ого поколения согласно закону Харди -Вайнберга для генотипов AA, Aa, aa имеем частоты:
аллелей A и a в n -ом поколении в момент его появления (они же - частоты гамет n-1 ого поколения). Первоначально для n -ого поколения согласно закону Харди -Вайнберга для генотипов AA, Aa, aa имеем частоты: 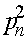 ,
, 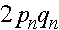 ,
, 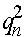 . Числа
. Числа 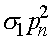 ,
, 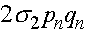 ,
, 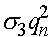 есть вероятности того, что особь n -ого поколения относится соответственно к генотипу AA, Aa, aa и доживает до этапа размножения. Полная вероятность того, что особь n - ого поколения доживает до размножения суть
есть вероятности того, что особь n -ого поколения относится соответственно к генотипу AA, Aa, aa и доживает до этапа размножения. Полная вероятность того, что особь n - ого поколения доживает до размножения суть
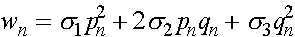 . (13)
. (13)
Эту величину будем называть средней приспособленностью в n -ом поколении. Используя формулу Бейеса (теорема гипотез), выписываем частоты генотипов AA, Aa, aa этого поколения к моменту начала этапа размножения:
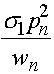 ,
, 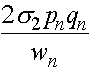 ,
, 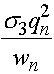 .
.
Частоты гамет A, a определяются частотами генотипов:
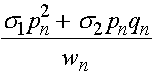 ,
, 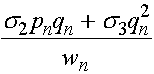 .
.
Частоты аллелей A, a в момент появления n+1 -ого поколения совпадают с частотами гамет предыдущего поколения. Получаем уравнения связывающие частоты аллелей:
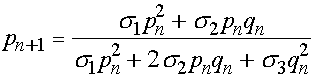 , (14)
, (14)
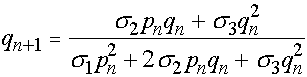 . (15)
. (15)
Независимым из этих двух уравнений является только одно т.к. 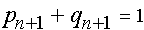 . Отметим, что уравнения (14) и (15) не меняются, если заменить
. Отметим, что уравнения (14) и (15) не меняются, если заменить 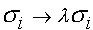 , где
, где 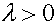 произвольно. В связи с этим часто принимают равной единице максимальную относительную приспособленность.
произвольно. В связи с этим часто принимают равной единице максимальную относительную приспособленность.
Уравнение (14) имеет явные решения только в частных случаях. Рассмотрим случай так называемого геометрического отбора. Пусть относительные приспособленности генотипов образуют геометрическую прогрессию: 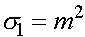 ,
, 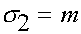 ,
, 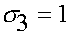 . Введем обозначения
. Введем обозначения 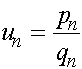 . Разделив первое уравнение на второе, получим
. Разделив первое уравнение на второе, получим
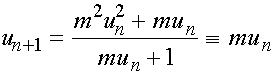 .
.
Отсюда следует, что 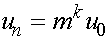 . Вернемся к старым переменным:
. Вернемся к старым переменным:
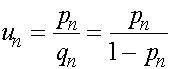 .
.
Получаем
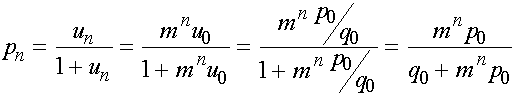 .
.
Если 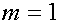 , то отбора нет,
, то отбора нет, 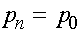 и для всех
и для всех 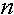 . Если
. Если 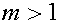 , то
, то 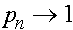 и
и 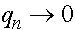 с ростом
с ростом 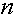 , т.е. аллель A вытесняет аллель a. Если
, т.е. аллель A вытесняет аллель a. Если 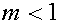 , то наоборот -аллель a вытесняет аллель A. Отбор геометрического типа эквивалентен отбору на уровне аллелей. Действительно, пусть
, то наоборот -аллель a вытесняет аллель A. Отбор геометрического типа эквивалентен отбору на уровне аллелей. Действительно, пусть 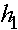 - вероятность того что, особь, имеющая один аллель A, доживет до стадии размножения. В свою очередь, пусть
- вероятность того что, особь, имеющая один аллель A, доживет до стадии размножения. В свою очередь, пусть 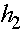 аналогичная вероятность по аллелю a. Данные вероятности можно понимать как вероятности выживания аллелей и можно назвать приспособленностью аллелей. Если считать, что гибель аллеля приводит к гибели особи, то вероятности выживания (приспособленности) особей генотипов AA, Aa, aa суть
аналогичная вероятность по аллелю a. Данные вероятности можно понимать как вероятности выживания аллелей и можно назвать приспособленностью аллелей. Если считать, что гибель аллеля приводит к гибели особи, то вероятности выживания (приспособленности) особей генотипов AA, Aa, aa суть 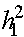 ,
, 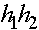 ,
, 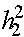 . Как уже отмечалось, приспособленности можно нормировать (разделить на одно и то же число). После деления на
. Как уже отмечалось, приспособленности можно нормировать (разделить на одно и то же число). После деления на 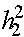 получим приспособленности генотипов
получим приспособленности генотипов 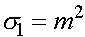 ,
, 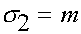 ,
, 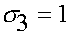 , где
, где 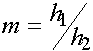 .
.
Рассмотрим случай летального
