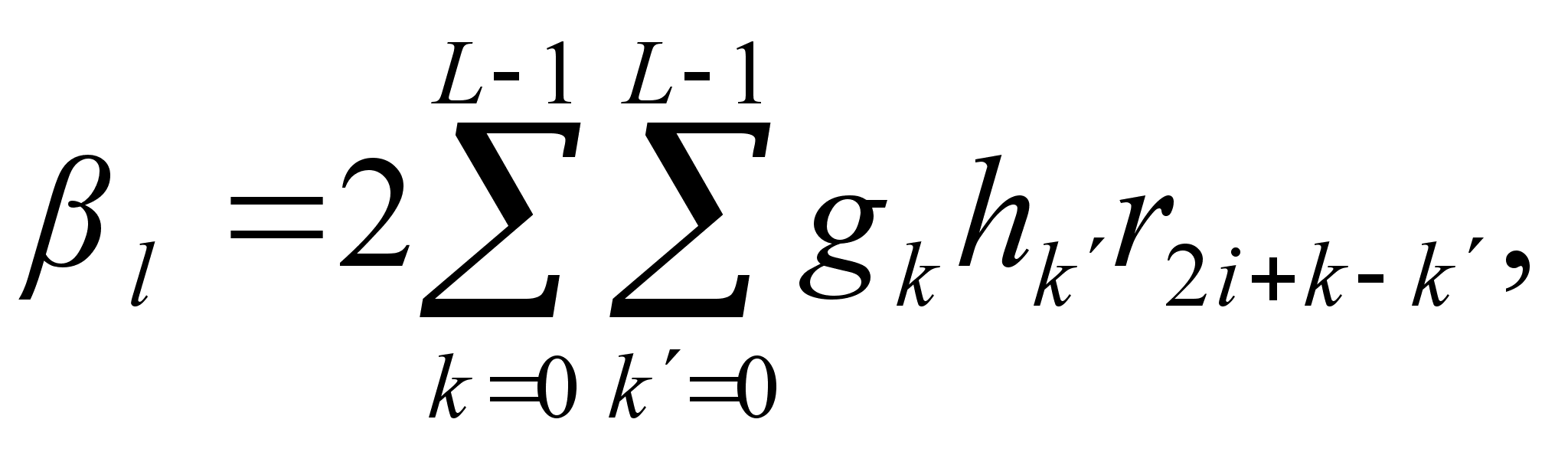Операторы в вейвлетном базисе
замены /2 на , получаем необходимое условие
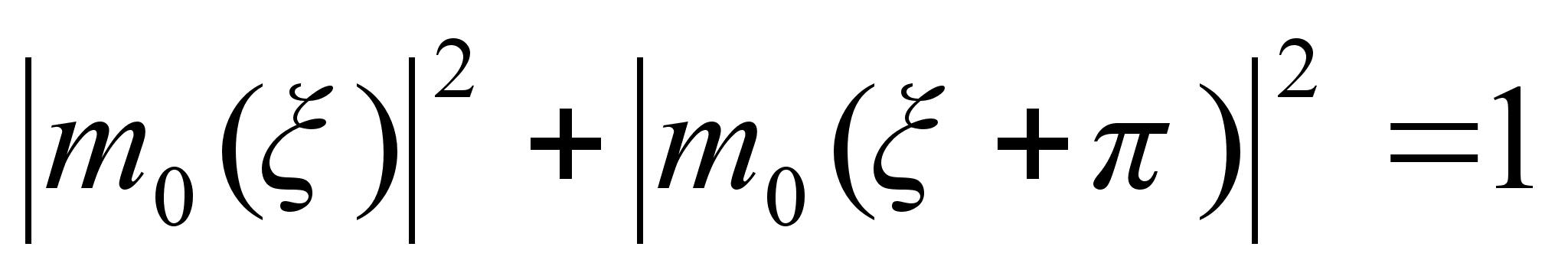 (1.17)
(1.17)
для коэффициентов hk в (1.11). Заметив, что
 (1.18)
(1.18)
и определив функцию следующим образом:
 ,
(1.19)
,
(1.19)
где
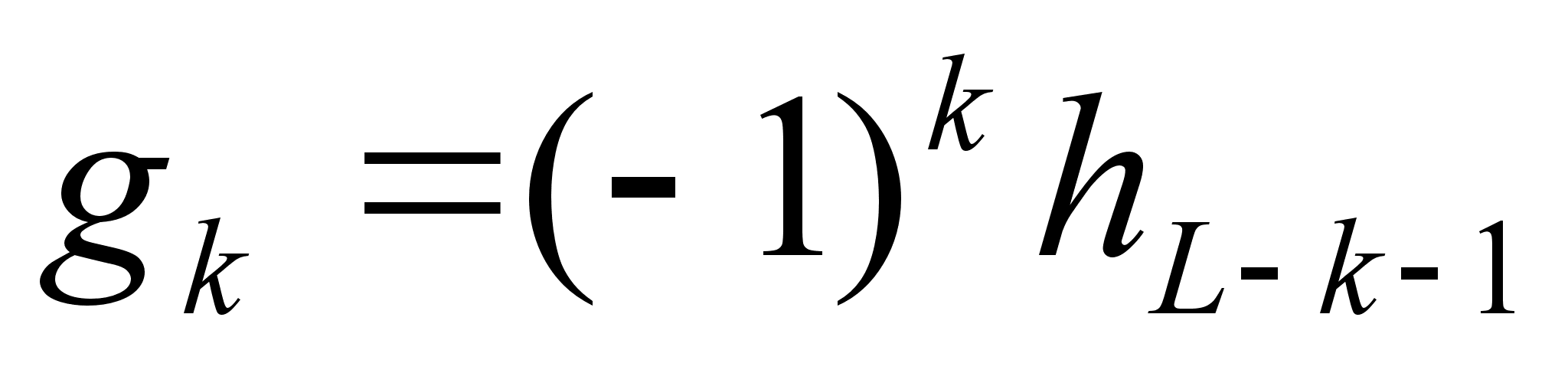 ,
k=0,…,L-1
, (1.20)
,
k=0,…,L-1
, (1.20)
или преобразование Фурье для
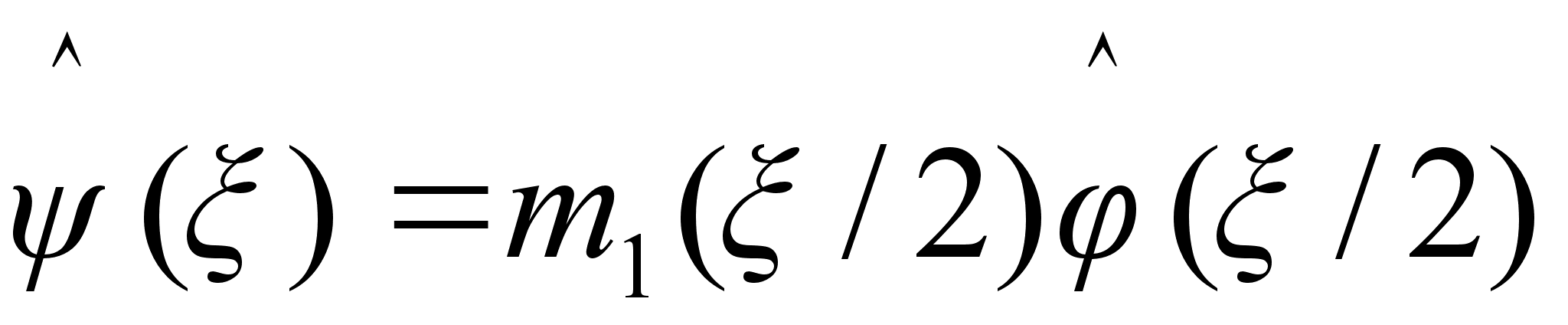 ,
(1.21)
,
(1.21)
где
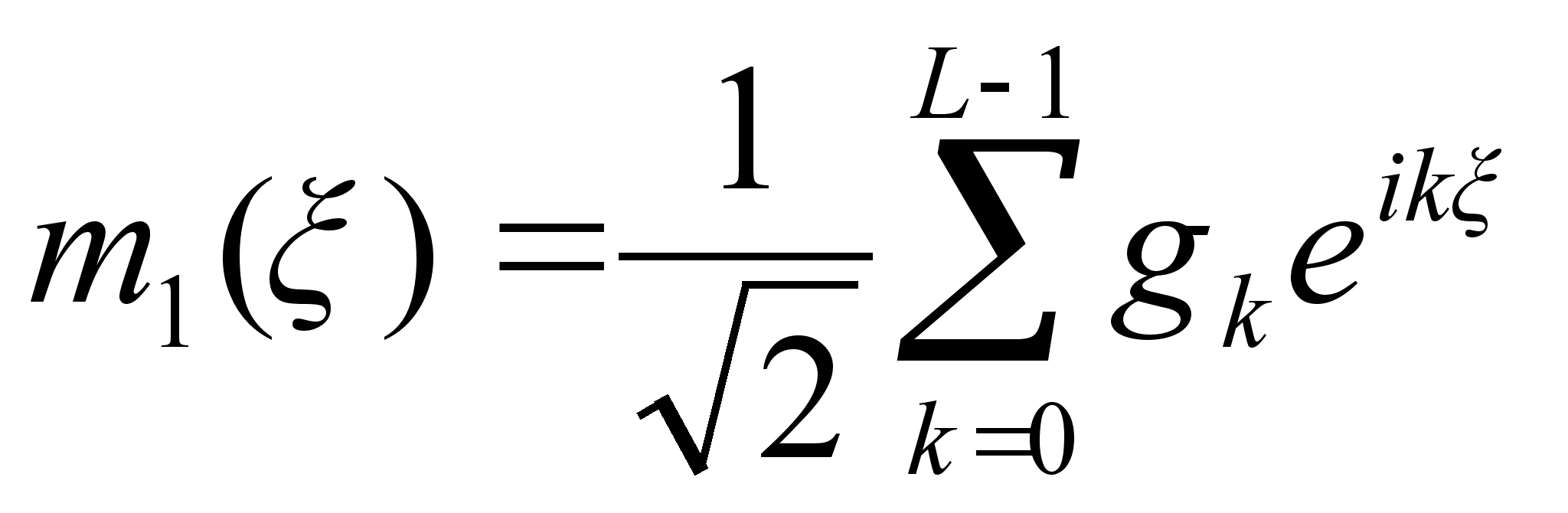 ,
(1.22)
,
(1.22)
можно показать, что при каждом фиксированном масштабе jZ вейвлеты
{j,k(x)=2-j/2(2-jx-k)}kZ образуют ортонормальный базис пространства Wj.
Равенство
(1.17) определяет
пару квадратурных
зеркальных
фильтров (quadrature
mirror filters, QMF) H
и G, где
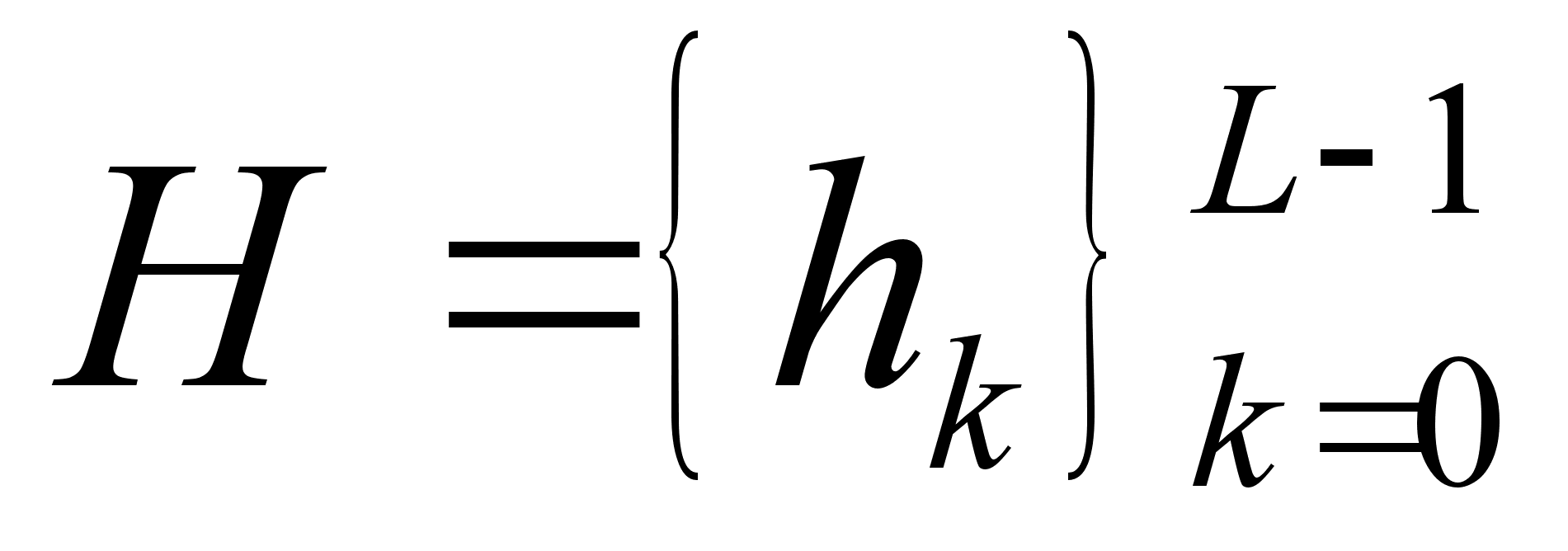 и
и
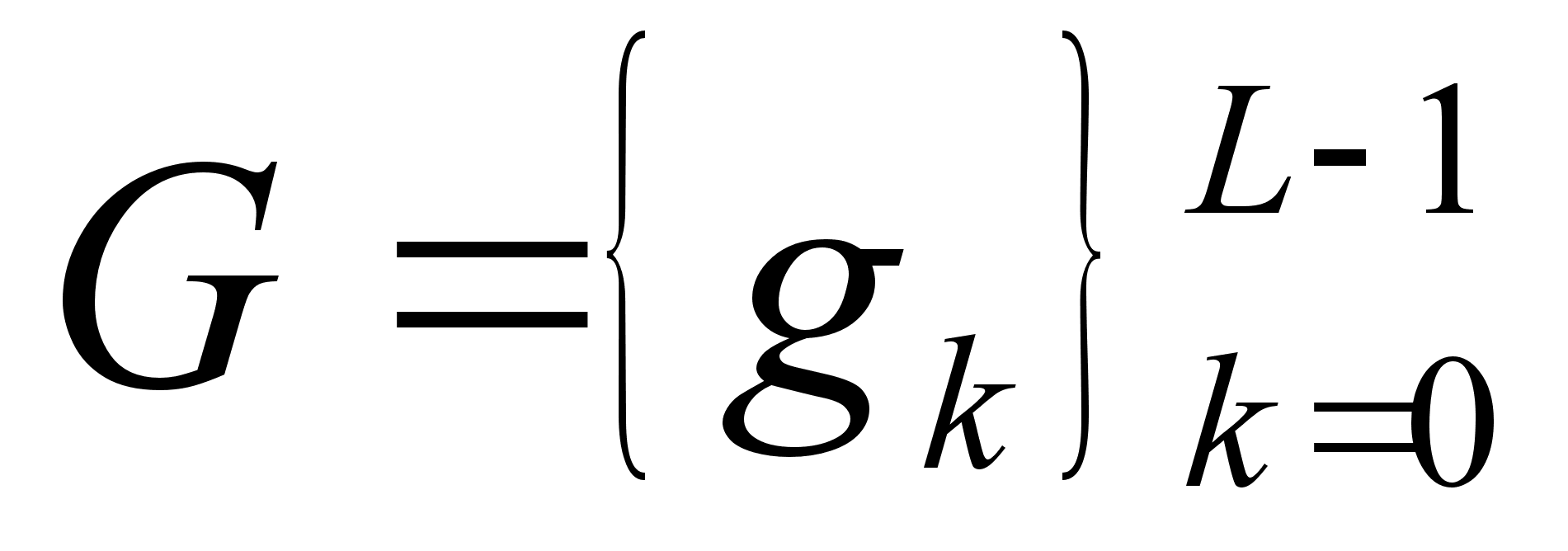 .
Коэффициенты
QMF H
и G вычисляются
с помощью решения
системы алгебраических
уравнений.
Число L
коэффициентов
фильтра в (1.11) и
(1.22) связано с
числом исчезающих
моментов М,
и всегда четно.
.
Коэффициенты
QMF H
и G вычисляются
с помощью решения
системы алгебраических
уравнений.
Число L
коэффициентов
фильтра в (1.11) и
(1.22) связано с
числом исчезающих
моментов М,
и всегда четно.
Выбранный фильтр Н полностью определяет функции и и, таким образом, многомасштабный анализ. Кроме того, в правильно построенных алгоритмах значения функций и почти никогда не вычисляются. Благодаря рекурсивному определению вейвлетного базиса, все операции проводятся с квадратурными зеркальными фильтрами H и G, даже если в них используются величины, связанные с и .
4. ОПЕРАТОРЫ
Сжатие операторов или, другими словами, представление их в разреженном виде в ортонормированном базисе непосредственно влияет на скорость вычислительных алгоритмов.
Нестандартная форма оператора Т с ядром K(x,y) достигается вычислением следующих выражений:
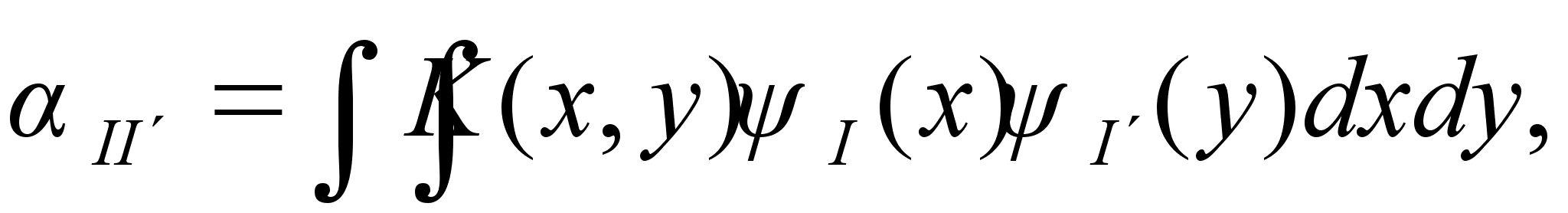 (4.1)
(4.1)
 (4.2)
(4.2)
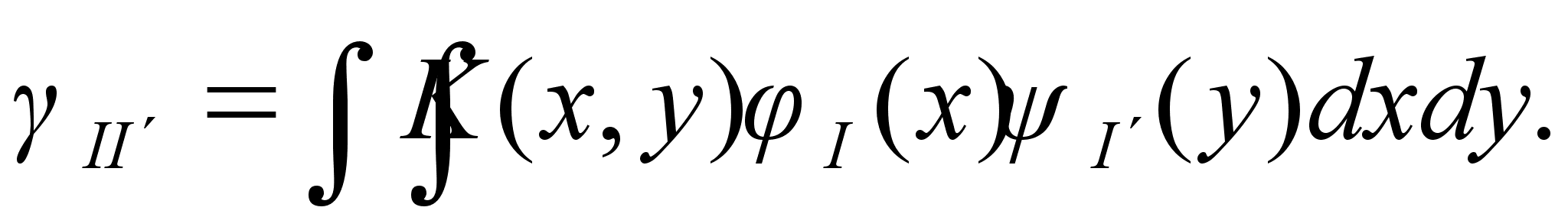 (4.3)
(4.3)
4.1 Оператор d/dx в вейвлетном базисе
Нестандартные
формы некоторых
часто используемых
операторов
могут быть
вычислены явно.
Построим
нестандартную
форму оператора
d/dx.
Матричные
элементы
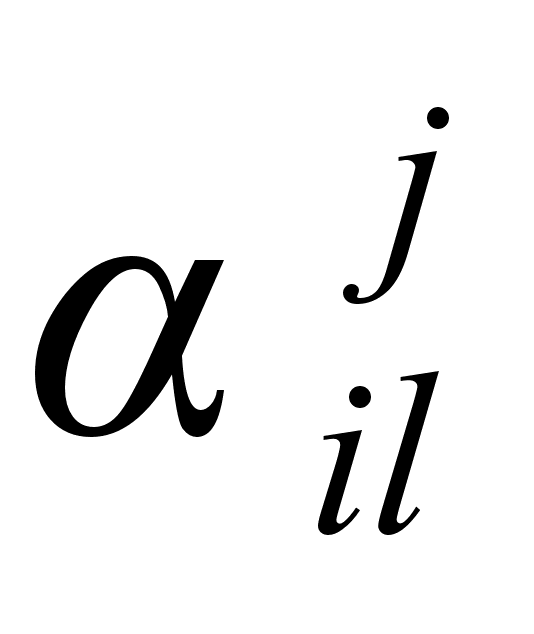 ,
,
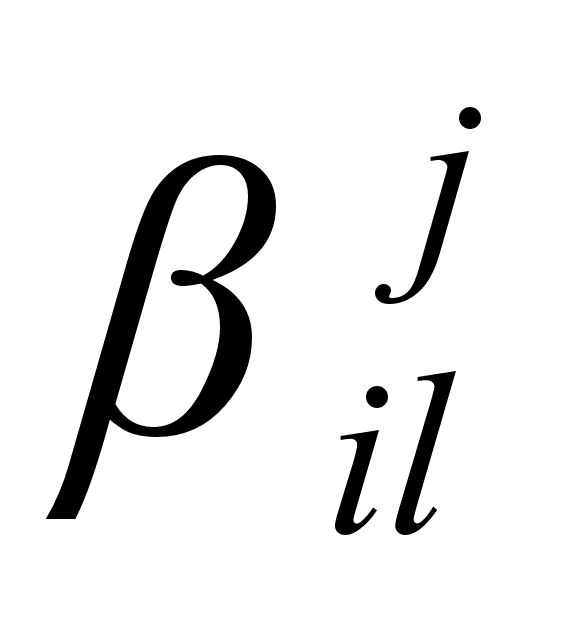 ,
,
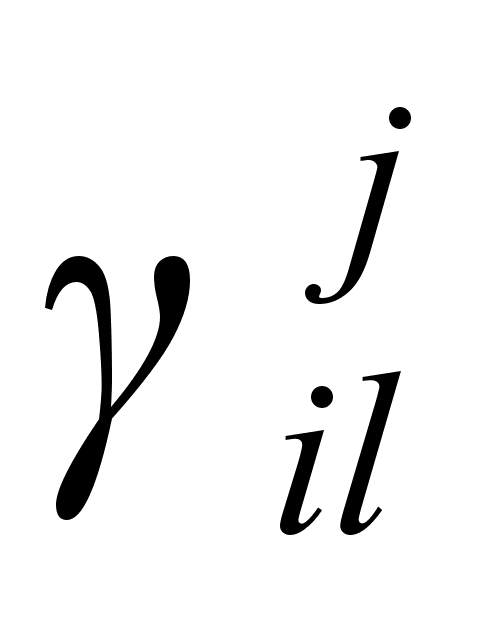 матриц
матриц
 ,
,
 ,
,
 и
и
 матрицы
матрицы
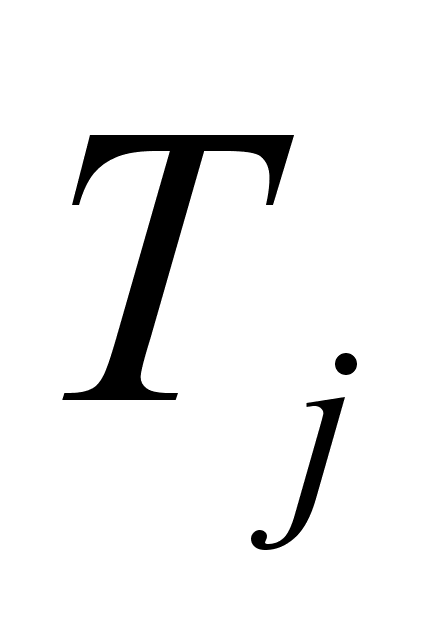 ,
где i, l,
j
Z для
оператора d/dx
легко вычисляются
как
,
где i, l,
j
Z для
оператора d/dx
легко вычисляются
как
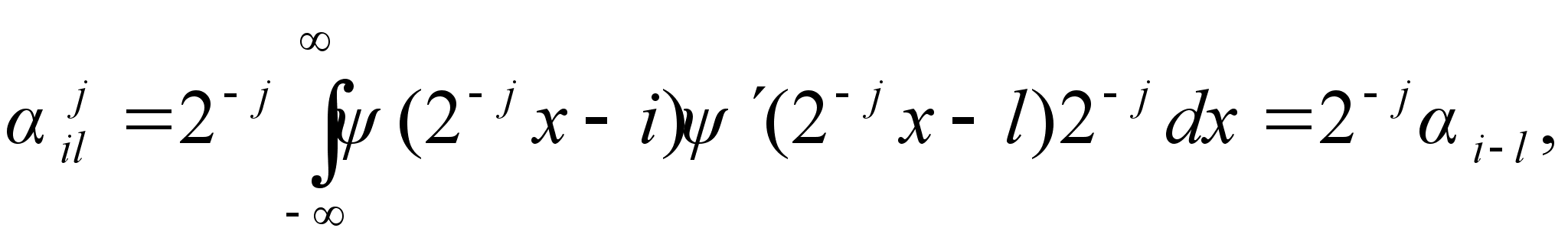 (4.4)
(4.4)
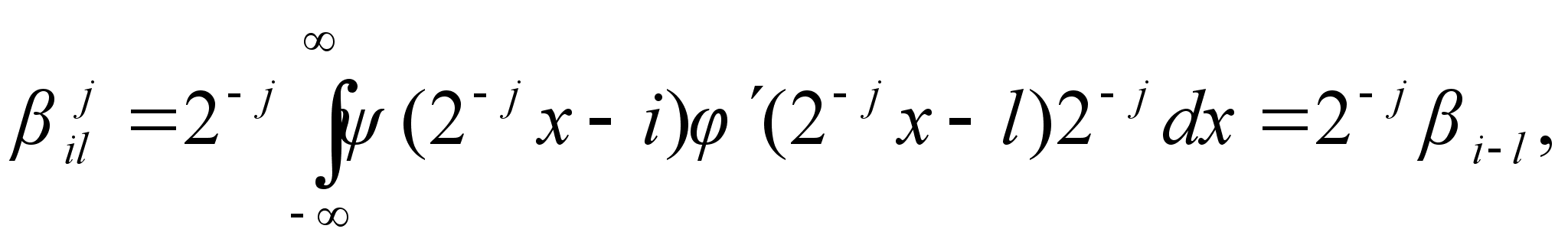 (4.5)
(4.5)
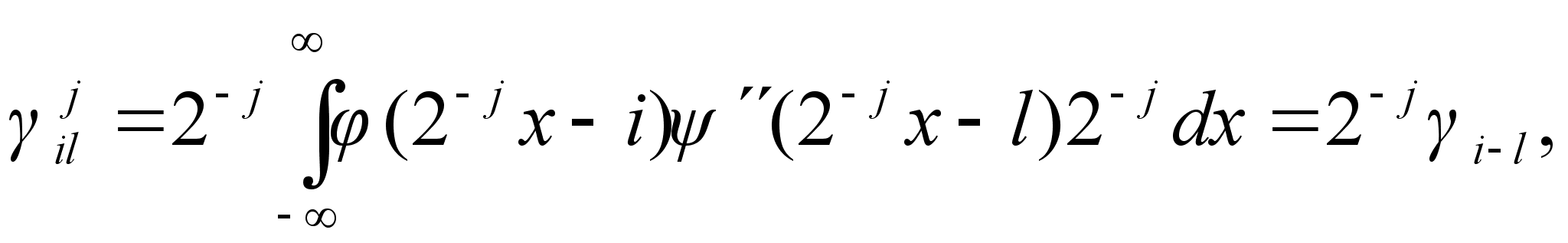 (4.6)
(4.6)
 (4.7)
(4.7)
где
 (4.8)
(4.8)
 (4.9)
(4.9)
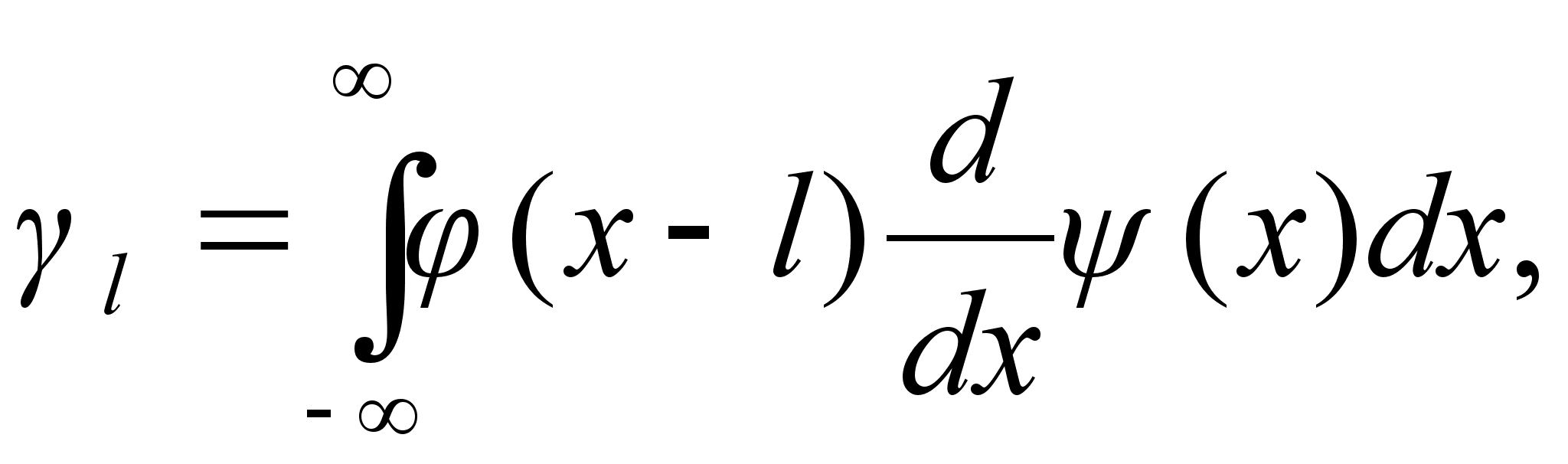 (4.10)
(4.10)
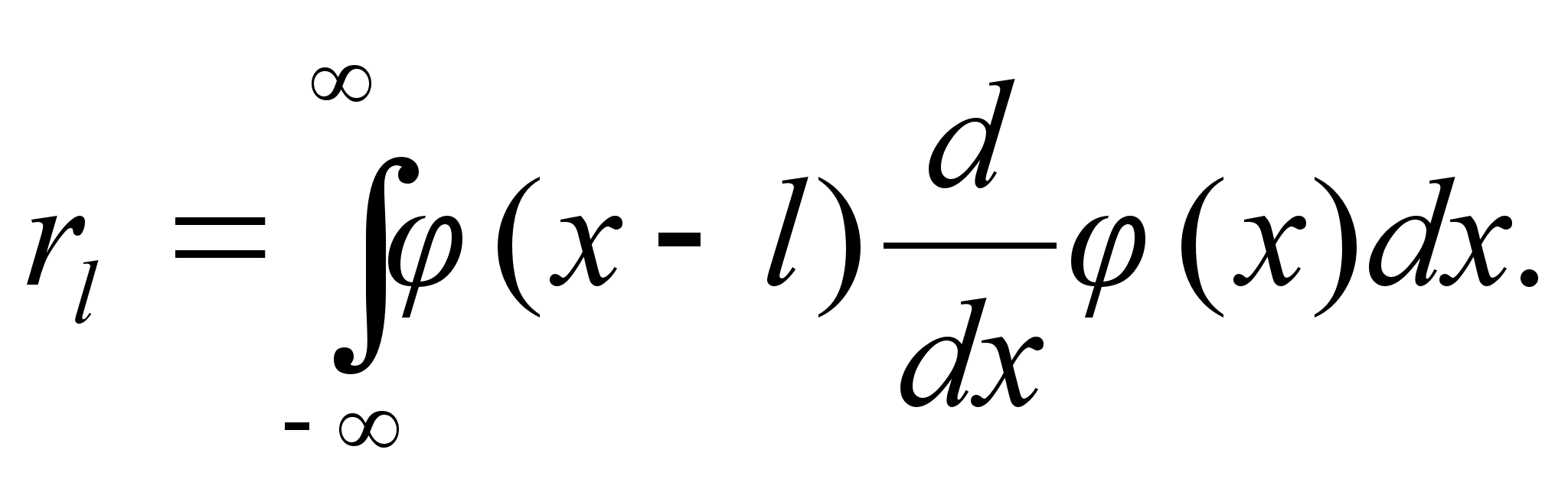 (4.11)
(4.11)
Кроме того, используя (1.8) и (1.19), имеем
 (4.12)
(4.12)