Алгоритми розрахунку періодичного режиму в нелінійній схемі

початкове значення вектора .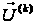

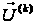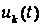Крок 2: розрахувати за формулою (14) та за компонентами вектора миттєві значення напруги в М точках періоду .

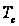Крок 3: розрахувати з вольт-амперної 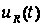та вольт-кулонівської 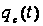характеристик миттєві значення струму крізь нелінійний опір та заряд на нелінійній ємності в М точках періоду 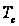, а також розрахувати компоненти векторів 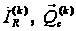за допомогою дискретного перетворення Фур’є.

Крок 4: визначити вектор незв’язності 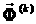за допомогою (11), (12).

Крок 5: перевірити виконання нерівності 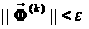; якщо вона виконується, то закінчити; якщо ні, то перейти до кроку 6.

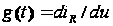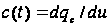Крок 6: розрахувати миттєві значення і в М точках на періоді та знайти за допомогою дискретного перетворення Фур’є спектральний склад g(t) і c(t).

Крок 7: сформувати матрицю Якобі, користуючись (10), (11), (12).

Крок 8: вирішити систему лінійних рівнянь (12) відносно компонент вектора 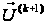; покласти 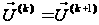і повернутися до кроку 2.

Обміркуємо особливості розрахунку періодичного режиму автогенератора. Припустимо, в схемі (рис. 1) джерело струму замінили джерелом живлення 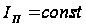, який задає робочу точку на нелінійних елементах. Припустимо, що в вольт-амперній характеристиці нелінійного опору є спадаюча ділянка, в середині якої вибрана робоча точка. За цих умов у схемі можуть збудитись автоколивання, які описуються рівнянням, складеним для змінних напруги, струму і заряду відносно робочої точки

.

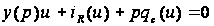Якщо в це рівняння підставити (11), (12), (13) і зробити, як раніше, ряд перетворень, то можна отримати рівняння (8), в яких 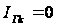, , 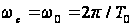де 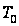- невідомий період. Таким чином, кількість невідомих на одиницю більше, ніж кількість рівнянь. Щоб привести у відповідність кількість невідомих і рівнянь, вважаємо

.

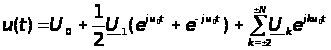З цього виразу випливає, що перша гармоніка напруги не має квадратурної (синусної) складової. Такий запис справедливий тому, що в автогенераторі фаза коливань випадкова. В результаті кількість спектральних складових напруги зменшилась на одиницю.

Щоб виразніше уявити специфіку розрахунку, підставимо в (8) N=1 і запишемо систему рівнянь автогенератора в дійсній формі

,

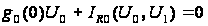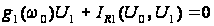, (14)

.

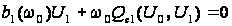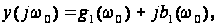
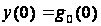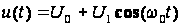Тут позначено . Оскільки прийнято , то

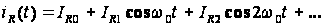
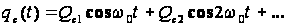
Якщо маємо аналітичну залежністю 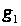і 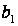від частоти 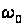, то можна ввести вектор 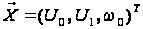, записати рівняння (14) у вигляді 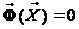і вирішити їх методом Ньютона. При цьому для елементів матриці Якобі вдається утворити аналітичний вираз і алгоритм розрахунків збігається з попереднім.

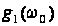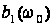Якщо програма не орієнтована на отримання аналітичного виразу для і , то можна зробити таким чином. Подамо перші два рівняння до (14) у векторно-матричної формі

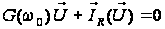, (15)

а останнє перепишемо як

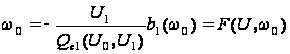, (16)

де - діагональна матриця;

, .

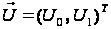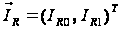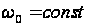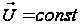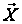Вирішуватимемо (15) методом Ньютона при , а (16) послідовним зближенням або методом Стефенсена при . Обчислення повинні бути організовані так, щоб після вирішення одного рівняння його результати вводились в друге як початкові значення і навпаки. Розрахунки припиняються, якщо норма різності векторів на сусідніх ітераціях стане менша, ніж задана похибка.

Размещено на