Линейно упорядоченное пространство ординальных чисел
= f (y) (по предложению 5.10). Следовательно, если f продолжить на пространство W( 1)
1)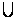 {
{ 1},
являющееся
одноточечной
компактификацией
пространства
W(
1},
являющееся
одноточечной
компактификацией
пространства
W( 1),
положив
1),
положив
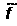 (
( 1)
= f (х), где х >a,
1)
= f (х), где х >a,
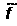 |W(
|W( 1)
= f , то мы получим
непрерывную
функцию
1)
= f , то мы получим
непрерывную
функцию
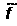 на W(
на W( 1)
1)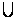 {
{ 1}.
Значит, W(
1}.
Значит, W( 1)
1)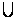 {
{ 1}
– расширение
Стоуна-Чеха
пространства
W(
1}
– расширение
Стоуна-Чеха
пространства
W( 1).
■
1).
■СПИСОК ЛИТЕРАТУРЫ
1. Чиркова Н. В. Выпускная квалификационная работа «Линейно упорядоченные пространства», научный руководитель Варанкина В. И., Киров, 2002.
2. Александров П. С. «Введение в теорию множеств и общую топологию». М.: Наука, 1977.
3. Энгелькинг Р. «Общая топология». М.: Мир, 1986.
4. Келли Дж. Л. «Общая топология». М.: Наука, 1981.
5. А. Н. Колмогоров, С. В. Фомин «Элементы теории функций и функционального анализа». М.: Наука, 1968.
6. И. А. Лавров, Л. Л. Максимова «Задачи по теории множеств, математической логике и теории алгоритмов». М.: Физматлит, 1995.
7. Р. Столл «Множества. Логика. Аксиоматические теории». М.: Просвещение, 1968.
8. Ч. Коснёвски «Начальный курс алгебраической топологии». М.: Мир, 1983.
