Беселеві функції
є:
 .
.
Маємо:
 ,
,
 ,
,
звідки після по членного перемножування цих рівностей знайдемо:
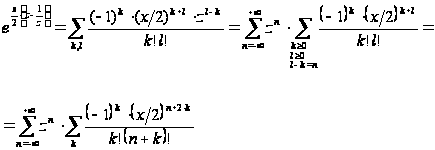
(тому що
в передостанній
внутрішній
сумі
 й
й
 були зв'язані
залежністю
були зв'язані
залежністю
 ,
то ми могли
покласти
,
то ми могли
покласти
 ,
одержавши
підсумовування
по одному індексі
,
одержавши
підсумовування
по одному індексі
 ).
В останній
внутрішній
сумі підсумовування
виробляється
по всіх цілих
).
В останній
внутрішній
сумі підсумовування
виробляється
по всіх цілих
 ,
для яких
,
для яких
 ,
отже, при
,
отже, при
 це буде
це буде
 ;
при
;
при
 це буде
це буде
 .
Таким чином,
у всіх випадках
внутрішня сума
є
.
Таким чином,
у всіх випадках
внутрішня сума
є
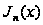 в силу формул
(5`) і (5```). Отже,
в силу формул
(5`) і (5```). Отже,
 , (18)
, (18)
але це
й доводить, що
 є виробляюча
функція для
системи
є виробляюча
функція для
системи
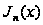 .
.
Виведемо
деякі наслідки
з формули (18).
Думаючи в ній
 ,
одержимо:
,
одержимо:
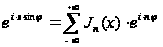 ,
,
звідки
після поділу
дійсної й мнимої
частини (з огляду
на, що
 )
)
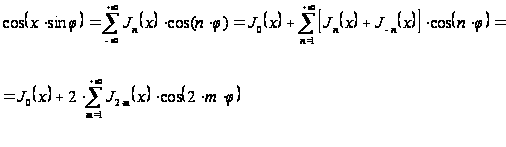 (18`)
(18`)
 (18``)
(18``)
Заміняючи
в (18`) і (18``)
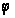 на
на
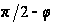 ,
знайдемо:
,
знайдемо:
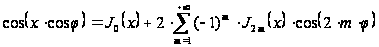 ,
(18```)
,
(18```)
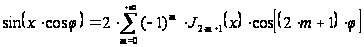 . (18````)
. (18````)
Інтегральне подання Jn(x)
Тому що,
по доведеному,
при
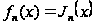 маємо
маємо
 ,
те по формулі
(17) одержуємо
(використовуючи
в перетвореннях
формули Ейлера):
,
те по формулі
(17) одержуємо
(використовуючи
в перетвореннях
формули Ейлера):
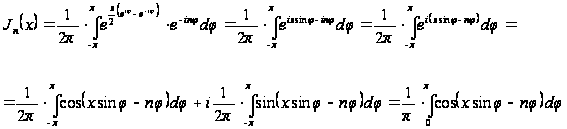
де прийнято
в увагу, що
 є парна функція
від
є парна функція
від
 є непарна функція
від
є непарна функція
від
 .
Отже, доведено,
що для будь-якого
цілого числа
.
Отже, доведено,
що для будь-якого
цілого числа
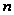
 . (19)
. (19)
Формула
(19) дає подання
Беселевих
функцій із
цілим індексом
у вигляді певного
інтеграла, що
залежить від
параметра
 .
Ця формула
називається
інтегральним
поданням Беселя
для
.
Ця формула
називається
інтегральним
поданням Беселя
для
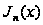 ,
права частина
формули називається
інтегралом
Беселя. Зокрема,
при
,
права частина
формули називається
інтегралом
Беселя. Зокрема,
при
 знайдемо:
знайдемо:
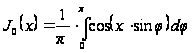 . (19`)
. (19`)
5. Ряди Фур'є-Беселя
Розглянемо
на якому-небудь
інтервалі
 (кінцевому або
нескінченному)
два диференціальних
рівняння
(кінцевому або
нескінченному)
два диференціальних
рівняння
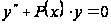 ,
,
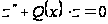 , (20)
, (20)
де
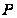 й
й
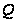 – безперервні
функції на
– безперервні
функції на
 .
Нехай
.
Нехай
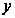 і
і
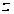 – ненульові
рішення цих
рівнянь. Множення
на
– ненульові
рішення цих
рівнянь. Множення
на
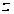 й на
й на
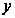 й наступне
вирахування
дають
й наступне
вирахування
дають
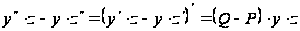 .
.
Нехай
 і
і
 належать
належать
 і
і
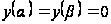 ,
тоді після
інтегрування
в межах від
,
тоді після
інтегрування
в межах від
 до
до
 одержимо
одержимо
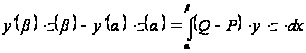 . (21)
. (21)
Якщо
 й
й
 – сусідні нулі
рішення
– сусідні нулі
рішення
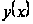 ,
то між
,
то між
 і
і

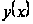 зберігає постійний
знак, нехай,
наприклад,
зберігає постійний
знак, нехай,
наприклад,
 на (
на ( ,
,
 )
(у противному
випадку варто
замінити
)
(у противному
випадку варто
замінити
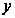 на
на
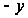 ),
тоді
),
тоді
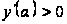 ,
,
 (рівність нулю
виключено, тому
що
(рівність нулю
виключено, тому
що
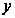 – ненульове
рішення диференціального
рівняння другого
порядку). Якщо
на
– ненульове
рішення диференціального
рівняння другого
порядку). Якщо
на

 ,
то
,
то
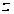 повинна, принаймні,
раз звертатися
в нуль між
повинна, принаймні,
раз звертатися
в нуль між
 і
і
 ,
тому що інакше
,
тому що інакше
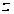 збереже постійний
знак на (
збереже постійний
знак на ( ,
, ).
Нехай, наприклад,
).
Нехай, наприклад,
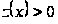 на (
на ( ,
, )
(у противному
випадку заміняємо
)
(у противному
випадку заміняємо
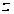 на
на
 ),
і тоді з (21) одержимо
протиріччя,
тому що ліва
частина ≤0, а
права >0. У такий
спосіб доведена
теорема порівняння
Штурму: якщо
P(x)<Q(x) на розглянутому
інтервалі I і
якщо y і z – ненульові
рішення рівнянь
(20), те між кожними
двома сусідніми
нулями y(x) перебуває
принаймні один
нуль z(x).
),
і тоді з (21) одержимо
протиріччя,
тому що ліва
частина ≤0, а
права >0. У такий
спосіб доведена
теорема порівняння
Штурму: якщо
P(x)<Q(x) на розглянутому
інтервалі I і
якщо y і z – ненульові
рішення рівнянь
(20), те між кожними
двома сусідніми
нулями y(x) перебуває
принаймні один
нуль z(x).
З теореми
порівняння
Штурму випливають
нижченаведені
наслідки. Якщо
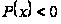 на
на
 ,
то кожне ненульове
рішення рівняння
,
то кожне ненульове
рішення рівняння
 може мати на
може мати на
 не більше одного
нуля (це легко
бачити, якщо
покласти
не більше одного
нуля (це легко
бачити, якщо
покласти
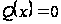 й взяти
й взяти
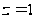 ).
Якщо
).
Якщо
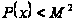 на
на
 (де
(де
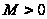 ),
то для всяких
двох сусідніх
нулів
),
то для всяких
двох сусідніх
нулів
 і
і
 (
( )
кожного ненульового
рішення рівняння
)
кожного ненульового
рішення рівняння
 маємо
маємо
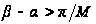 (це легко бачити,
якщо покласти
(це легко бачити,
якщо покласти
 ,
взяти
,
взяти
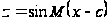 й помітити, що
нулями
й помітити, що
нулями
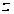 будуть тільки
числа виду
будуть тільки
числа виду
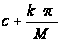 ,
,
 ціле). Якщо
ціле). Якщо
 на
на
 (де
(де
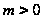 ),
то для всяких
двох сусідніх
нулів кожного
ненульового
рішення рівняння
),
то для всяких
двох сусідніх
нулів кожного
ненульового
рішення рівняння
 маємо
маємо
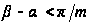 (це легко бачити,
якщо покласти
(це легко бачити,
якщо покласти
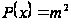 й взяти
й взяти
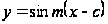 ).
Із сказаного
випливає, що
якщо
).
Із сказаного
випливає, що
якщо
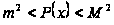 на
на
 ,
те для всяких
двох сусідніх
нулів
,
те для всяких
двох сусідніх
нулів
 і
і
 (
( )
кожного ненульового
рішення рівняння
)
кожного ненульового
рішення рівняння
 маємо
маємо
 .
.
Викладене
показує, що
якщо
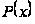 безперервно
на
безперервно
на
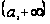 й перевищує
деяке позитивне
число поблизу
+∞, те кожне
ненульове
рішення
й перевищує
деяке позитивне
число поблизу
+∞, те кожне
ненульове
рішення
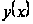 рівняння
рівняння має на
має на
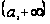 нескінченно
багато нулів.
Якщо ще
нескінченно
багато нулів.
Якщо ще
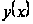 поблизу
поблизу
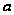 не звертається
в нуль, то ці
нулі утворять
нескінченну
зростаючу
послідовність
не звертається
в нуль, то ці
нулі утворять
нескінченну
зростаючу
послідовність
 ,
що має межею
+∞, а якщо, крім
того,
,
що має межею
+∞, а якщо, крім
того,
 ,
де
,
де
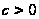 ,
те
,
те
 .
.
Розглянемо рівняння Беселя
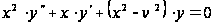
на інтервалі
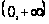 .
Підстановка
.
Підстановка
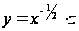 приводить до
рівняння
приводить до
рівняння
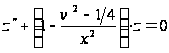 .
.
Очевидно,
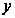 і
і
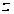 мають ті самі
нулі. Тому що
мають ті самі
нулі. Тому що
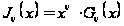 ,
де
,
де
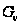 – ціла функція,
то
– ціла функція,
то
 не має нулів
на
не має нулів
на
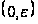 при досить
малому
при досить
малому
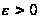 ,
і тому що
,
і тому що
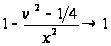 при
при
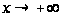 ,
те при кожному
,
те при кожному
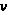 нулі
нулі
 на
на
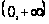 утворять нескінченну
зростаючу
послідовність
утворять нескінченну
зростаючу
послідовність
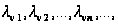
причому
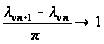 .
.
Якщо
 ,
то
,
то
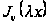 задовольнить
рівнянню
задовольнить
рівнянню
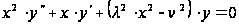
на інтервалі
(0, +∞). Підстановка
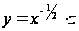 приводить до
рівняння
приводить до
рівняння
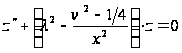
і, отже,
 задовольняє
цьому рівнянню.
Таким чином,
при будь-яких
позитивних
задовольняє
цьому рівнянню.
Таким чином,
при будь-яких
позитивних
 і
і
 маємо
маємо
 ,
де
,
де
 ,
,
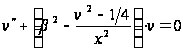 ,
де
,
де
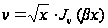 ,
,
звідки
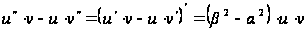 ,
,
отже,
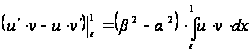 ,
де
,
де
 . (22)
. (22)
Нехай
тепер
 .
Розкладання
.
Розкладання
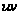 по ступенях
по ступенях
 починається
зі члена, що
містить
починається
зі члена, що
містить
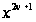 ,
розкладання
,
розкладання
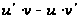 по ступенях
по ступенях
 починається
зі члена, що
містить
починається
зі члена, що
містить
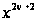 ,
тому що коефіцієнт
при
,
тому що коефіцієнт
при
 дорівнює нулю,
що легко бачити,
виходячи з
формули (5). Отже,
з (22) при
дорівнює нулю,
що легко бачити,
виходячи з
формули (5). Отже,
з (22) при
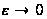 одержимо
одержимо
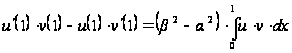 ,
,
тобто
 , (23)
, (23)
звідки
видно, що якщо
 і
і
 є різними нулями
функції
є різними нулями
функції
 ,
те
,
те
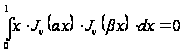 . (23`)
. (23`)
Цим доведено,
що при
 система функцій
система функцій
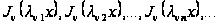
на інтервалі
 є ортогональної
щодо ваги
є ортогональної
щодо ваги
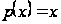 .
.
Переходячи
до межі при
 в співвідношенні
в співвідношенні
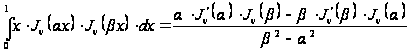
і використовуючи
правило Лопиталя,
одержимо при
всякому
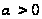
 ,
(24)
,
(24)
отже, якщо
 є нулем функції
є нулем функції
 ,
те
,
те
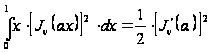 . (24`)
. (24`)
Таким
чином, при кожному
 всякій безперервній
функції
всякій безперервній
функції
 на
на
 ,
що задовольняє
вимозі
,
що задовольняє
вимозі
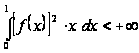 ,
,
поставлений у відповідність ряд Фур'є-Беселя
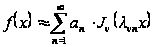 , (25)
, (25)
коефіцієнти якого визначаються формулами
 . (25`)
. (25`)
Можна
довести, що
система функцій
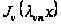 на
на
 ,
ортогональна
щодо ваги
,
ортогональна
щодо ваги
 ,
замкнута. Зокрема,
якщо ряд Фур'є-Беселя
(25) рівномірно
сходиться до
його безперервної
функції, що
,
замкнута. Зокрема,
якщо ряд Фур'є-Беселя
(25) рівномірно
сходиться до
його безперервної
функції, що
 породжує.
породжує.
Можна
показати, що
якщо
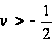 й
й
 безперервна
на
безперервна
на

