Беселеві функції
функції" width="32" height="24" align="BOTTOM" border="0" /> й функція, то ряд Фур'є-Беселя цієї функції сходиться до неї при .
.6. Асимптотичне подання Беселевих функцій із цілим індексом для більших значень аргументу
Нехай
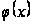 – позитивна
функція й
– позитивна
функція й
 – яка-небудь
функція для
досить більших
значень
– яка-небудь
функція для
досить більших
значень
 .
Запис
.
Запис
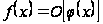 при
при
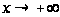
означає,
що найдуться
такі числа
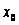 й M, що при
й M, що при
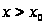 маємо
маємо
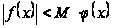 .
.
Подібний
запис уживається
й в інших аналогічних
випадках. Наприклад,
якщо
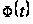 – позитивна
функція й
– позитивна
функція й
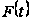 – яка-небудь
функція, визначені
для досить
малих позитивних
значень
– яка-небудь
функція, визначені
для досить
малих позитивних
значень
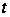 ,
то запис
,
то запис
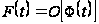 при
при
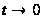
означає,
що найдуться
такі числа
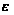 й
й
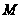 ,
що
,
що
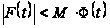 на
на
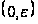 .
.
Допоміжна лема
Якщо
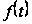 двічі безупинно
диференцюєма
на
двічі безупинно
диференцюєма
на
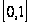 ,
то для функції
,
то для функції
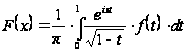
має місце асимптотичне подання
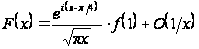 при
при
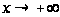 .
.
Доведемо
цю лему. Заміняючи
на
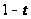 ,
одержимо:
,
одержимо:
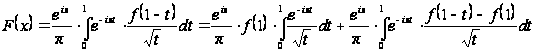 .(26)
.(26)
Розглянемо
інтеграл, що
фігурує в правої
частини формули
(20). Заміняючи
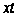 на
на
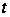 ,
знайдемо:
,
знайдемо:
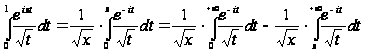 ,
,
але, замінивши
на
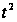 ,
одержимо:
,
одержимо:
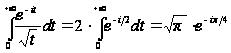 .
.
Якщо
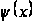 позитивно,
убуває й прагнути
до нуля при
позитивно,
убуває й прагнути
до нуля при
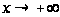 ,
то
,
то
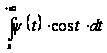 й
й
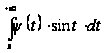 ,
а отже, і
,
а отже, і
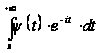 є
є
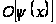 при
при
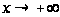 ,
тому
,
тому
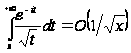 при
при
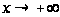 ,
,
звідки
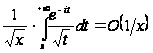 при
при
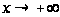 .
.
Отже, одержуємо асимптотичне подання:
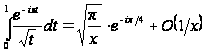 при
при
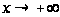 . (27)
. (27)
Розглянемо тепер інтеграл, що фігурує в другому складати^ся правої частини формули (20). Маємо:
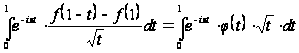 ,
,
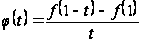 .
.
Очевидно,
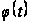 двічі безупинно
на
двічі безупинно
на
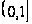 ,
але існують
,
але існують
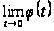 і
і
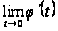 ,
тому
,
тому
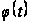 стає безупинно
диференцуєма
на
стає безупинно
диференцуєма
на
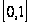 .
Інтегрування
вроздріб дає:
.
Інтегрування
вроздріб дає:
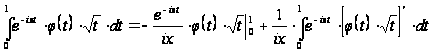 ,
,
де перший
доданок правої
частини
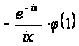 є
є
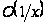 при
при
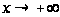 ,
а інтеграл у
другому мажорирується
інтегралом,
що складається
при нижній межі
,
а інтеграл у
другому мажорирується
інтегралом,
що складається
при нижній межі
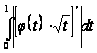 ,
,
який сходиться, тому що
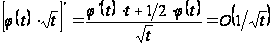 при
при
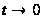 ;
;
отже,
другий доданок
є теж
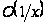 при
при
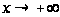 .
.
Отже, маємо:
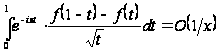 при
при
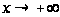 . (28)
. (28)
З (26), (27), (28) одержуємо шукане асимптотичне подання:
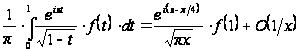 при
при
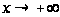 . (29)
. (29)
Із цієї формули, переходячи до сполучених величин, знайдемо ще:
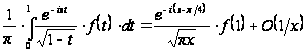 при
при
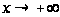 . (29')
. (29')
Формули
(29) і (29`) вірні й для
функцій
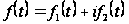 .
.
Висновок асимптотичної формули для Jn(x)
Заміняючи
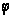 на
на
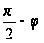 ,
одержимо:
,
одержимо:
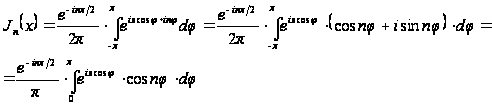
(з огляду
на, що
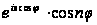 є парна функція
від
є парна функція
від
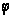 ,
а
,
а
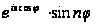 є непарна функція
від
є непарна функція
від
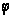 ).
Підстановка
).
Підстановка
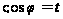 дає:
дає:
 ,
,
де
 є, мабуть, поліном
n-й ступеня (поліном
Чебишева), тому
що з формули
Муавра видно,
що
є, мабуть, поліном
n-й ступеня (поліном
Чебишева), тому
що з формули
Муавра видно,
що
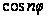 є поліном n-й
ступеня відносно
є поліном n-й
ступеня відносно
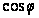 .
Але
.
Але
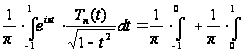
і, заміняючи
в першому із
цих інтегралів
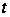 на
на
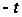 ,
одержимо:
,
одержимо:
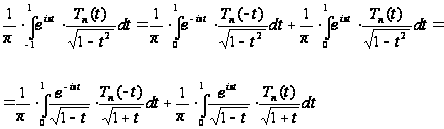
Тому що
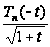 й
й
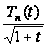 на
на
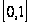 мають похідні
всіх порядків,
то до двох останніх
інтегралів
застосовні
формули (29) і (29`),
і ми одержуємо:
мають похідні
всіх порядків,
то до двох останніх
інтегралів
застосовні
формули (29) і (29`),
і ми одержуємо:
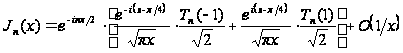 ;
;
але
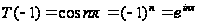 ;
;
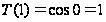 ,
отже,
,
отже,
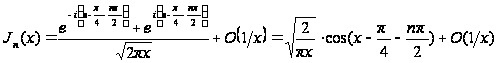 .
.
Отже, маємо шукане асимптотичне подання беселевої функції першого роду із цілим індексом для більших значень аргументу:
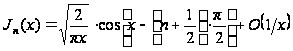 при
при
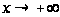 . (30)
. (30)
Ця формула
показує, що
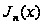 з точністю
складається
до порядку, що,
з точністю
складається
до порядку, що,
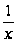 є загасаючою
гармонікою
із хвилею постійної
довжини й амплітудою,
що убуває обернено
пропорційно
квадратному
кореню з абсциси.
є загасаючою
гармонікою
із хвилею постійної
довжини й амплітудою,
що убуває обернено
пропорційно
квадратному
кореню з абсциси.
Зокрема,
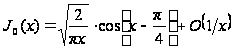 при
при
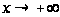 ; (30`)
; (30`)
 при
при
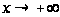 . (30'')
. (30'')
Графіки цих функцій зображені ні малюнках 1 і 2.
Розглянемо кілька прикладів рішення рівняння Беселя.
1. Знайти
рішення рівняння
Беселя при
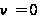
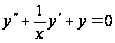 ,
,
задовольняючим
початковим
умовам при
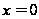 ,
,
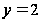 і
і
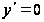 .
.
Рішення.
На підставі формули (5') знаходимо одне приватне рішення:
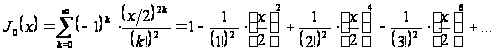 .
.
2. Знайти одне з рішень рівняння:
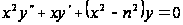 ,
,
 .
.
Рішення.
Зробимо заміну
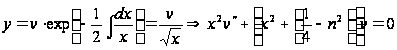 .
.
При
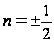 одержимо:
одержимо:
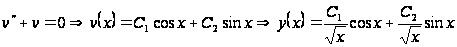 .
.
При
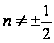 будемо шукати
рішення у вигляді
узагальненого
статечного
ряду:
будемо шукати
рішення у вигляді
узагальненого
статечного
ряду:
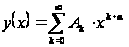 .
.
Рівняння
на
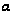 має вигляд
має вигляд
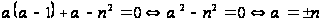 ;
;
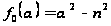 ,
,
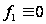 ,
,
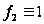 ,
,
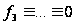 ,
тому
,
тому
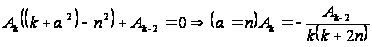 ,
,
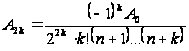 ,
,
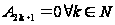 .
.
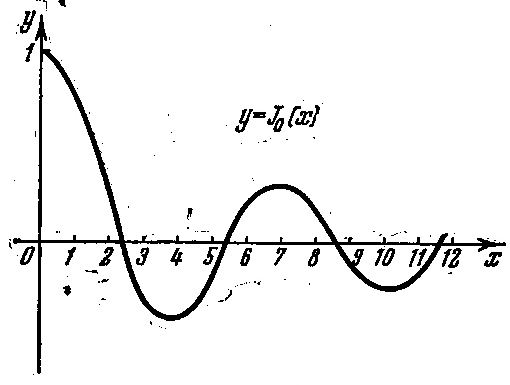
Рисунок 1 – Графік функції y=J0 (x)
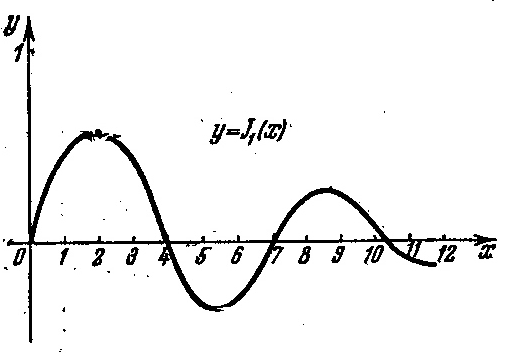
Рисунок 2 – Графік функції y=J1 (x)
Висновок
Розглянуті усі рішення рівнянь, які можуть бути представлені у вигляді добутку трьох функцій. Складені графіки функцій.
Список літератури
1. Пискунов Н.С. Диференціальне й інтегральне вирахування, навчальний посібник для вузів. – К., 2003
2. Романовський П. І. «Ряди Фур'є. Теорія поля. Аналітичні й спеціальні функції. Перетворення Лапласа», навчальний посібник для вузів. – К., 2004
3. Самарський А.А., Гулін А.В. Чисельні методи. – К., 2003
4. Синіцин О.К., Навроцкий А.А. Алгоритми обчислювальної математики. – К., 2003
