Функция многих переменных

align="BOTTOM" border="0" />

Решение. Сначала отделим переменные

,

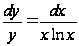а затем проинтегрируем

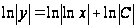, , у=Сlnx.

3. Функция 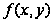называется однородной функцией п-го измерения относительно переменных х и у, если для произвольного числа выполняется тождество

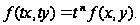
Пример 7.5.

1) =,

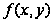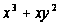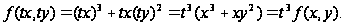
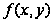- однородная функция третьего измерения.

2) 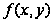=- однородная функция нулевого измерения.

Уравнение y’=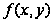называется однородным дифференциальным уравнением первого порядка, если функция 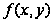является однородной функцией нулевого измерения, то есть, если

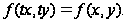(7.2)

Очевидно, уравнение вида

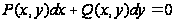
будет однородным тогда и только тогда, когда функции Р(х,у) и Q(х,у), будут однородными функциями одного и того же измерения. Например, уравнение

однородное. Считая, в соотношении (7.2) 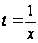, получим

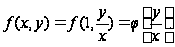
Поэтому можно дать ещё одно определение однородного уравнения: однородным дифференциальным уравнением называется уравнение вида

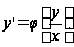(7.3)

Применим в уравнении (7.3) подстановку

, ,

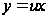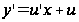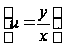
Тогда получим уравнение с разделяющимися переменными

,

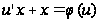которое всегда интегрируется в квадратурах:

,

.

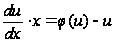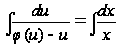После интегрирования надо сделать обратную замену, то есть вместо и нужно подставить

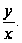
Вывод. Однородные дифференциальные уравнения первого порядка всегда сводятся к уравнениям с разделяющимися переменными подстановкой ,.

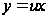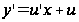Пример 7.6. Найти общее решение уравнения

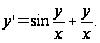
Решение. Применим подстановку 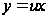,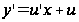. Тогда получим

,

, ,

, , .

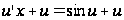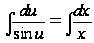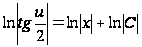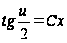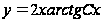Пример 7.7. Решить задачу Коши

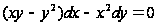, у(1)=2.

Решение. Поскольку обе функции

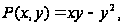
однородные измерения два, то данное уравнение однородное. Запишем его в виде

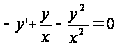
и применим подстановку 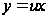,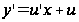. Тогда получим

,

, , .

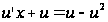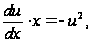
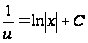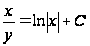Из начального условия найдём постоянную интегрирования:

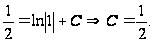
Подставив найденное значение С в общее решение, получим решение задачи Коши:

Лекция 16. Тема – Уравнения Бернулли. Комплексные числа. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

План.

1.Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли.

2. Комплексные числа.

3. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

1. Линейным дифференциальным уравнением первого порядка называется уравнение вида

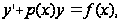(7.4)

где 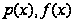- известные функции переменной х.

Термин «линейное уравнение» поясняется тем, что неизвестная функция у и её производная у’ входят в уравнение в первой степени, то есть линейно.

Линейное дифференциальное уравнение первого порядка всегда интегрируемо в квадратурах, поскольку его можно всегда свести к двум уравнениям с разделяющимися переменными таким образом (методом Бернулли).

Будем искать решение уравнения (7.4) в виде произведения

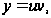(7.5)

где 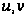- неизвестные функции х. Находя производную

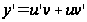
и подставляя значение у и у’ в уравнение (7.5), получим

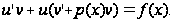(7.6)

Выберем функцию так, чтобы выражение в скобках равнялось нулю. Для этого надо решить уравнение с разделяющимися переменными.

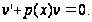
Решая его, находим

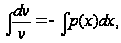
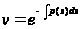. (7.7)

Постоянную интегрирования в выражении (7.7) не пишем, поскольку нам достаточно найти только какую-нибудь одну функцию , которая преобразовывает в ноль выражение в скобках в уравнении (7.6).

Подставляя (7.7) в (7.6), получим

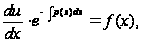
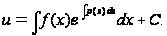(7.8)

Подставляя (7.7) и (7.8) в (7.5), найдём общее решение уравнения (7.4):

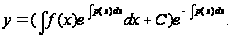(7.9)

Замечание. На практике помнить формулу (7.9) не обязательно: достаточно лишь помнить, что линейные дифференциальные уравнения первого порядка, а также уравнения Бернулли, решаются методом Бернулли с помощью подстановки .

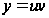Уравнением Бернулли называется уравнение вида

где 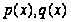- известные функции х, .

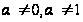2. Комплексным числом называется выражение

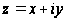, (7.10)

где х, у – действительные числа, а символ i – мнимая единица, которая определяется условием 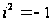. При этом число х называется действительной частью комплексного числа z и обозначается , а у – мнимой частью z и обозначается (от французских слов: reel – действительный, imaginare – мнимый). Выражение (7.10) называется алгебраической формой комплексного числа.

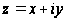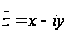Два комплексных числа и , которые отличаются только знаком мнимой части, называются сопряжёнными.

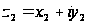Два комплексных числа и считаются равными тогда и только тогда, когда равны их действительные и мнимые части:

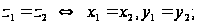
Комплексные числа можно изображать на плоскости. Так число (7.10) изображается в прямоугольной системе координат точкой М(х;у). Такая плоскость называется комплексной плоскостью переменной z, ось Ох называется действительной, у

а ось Оу – мнимой.

При у=0 комплексное число 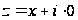является одновременно

у М(х;у)

действительным числом. Поэтому действительные числа являются

отдельным случаем комплексных, они изображаются на оси Ох.

Комплексные числа , в которых х=0, называются чисто

мнимыми; такие числа изображаются на оси Оу.

0 х х

Полярные координаты точки М(х;у) на комплексной плоскости называются модулем и аргументом комплексного числа и обозначаются

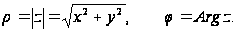
Поскольку 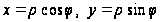, то по формуле (7.10) имеем

.

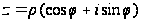Это выражение называется тригонометрической формой комплексного числа z.

Модуль комплексного числа определяется однозначно, а аргумент – с точностью до 2:

.

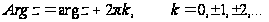Здесь 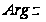- общее значение аргумента, а - главное значение аргумента, которое находится на промежутке [0;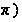 и отсчитывается от оси Ох против часовой стрелки.

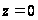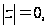Если , то считают, что а - неопределён.

Арифметические действия над комплексными числами, заданными в алгебраической форме, выполняются по обычным правилам действий над двучленами с учётом того, что