Нильпотентная длина конечных групп с известными добавлениями к максимальным подгруппам
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
Учреждение образования
"Гомельский государственный университет имени Франциска Скорины"
Математический факультет
Кафедра алгебры и геометрии
Допущена к защите
Зав. кафедрой Шеметков Л.А.
" " 2005г.
Дипломная работа
«Нильпотентная длина конечных групп с известными добавлениями к максимальным подгруппам»
Исполнитель
студентка группы М-51
Рубан Е.М.
Руководитель
Д. ф-м н., профессор Монахов В.С.
Гомель 2005
СОДЕРЖАНИЕ
Введение
1. Подгруппа Фиттинга и её свойства
2.
 -длина
-длина
 -разрешимой
группы
-разрешимой
группы
3. Группа с нильпотентными добавлениями к подгруппам
4. Используемые результаты
Заключение
Список использованных источников
ПЕРЕЧЕНЬ УСЛОВНЫХ ОБОЗНАЧЕНИЙ
Рассматриваются только конечные группы. Используются следующие обозначения.
 - простые
числа.
- простые
числа.
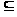 - знак
включения
множеств;
- знак
включения
множеств;
 - знак
строгого включения;
- знак
строгого включения;
 и
и
 - соответственно
знаки пересечения
и объединения
множеств;
- соответственно
знаки пересечения
и объединения
множеств;
 - пустое
множество;
- пустое
множество;
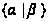 - множество
всех
- множество
всех
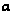 для которых
выполняется
условие
для которых
выполняется
условие
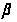 ;
;
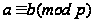 - число
- число
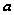 сравнимо с
числом
сравнимо с
числом
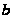 по модулю
по модулю
 .
.
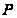 - множество
всех простых
чисел;
- множество
всех простых
чисел;
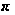 - некоторое
множество
простых чисел,
т.е.
- некоторое
множество
простых чисел,
т.е.
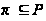 ;
;
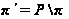 - дополнение
к
- дополнение
к
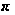 во множестве
всех простых
чисел; в частности,
во множестве
всех простых
чисел; в частности,
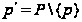 ;
;
примарное
число - любое
число вида
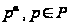 ,
,
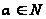 ;
;
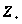 - множество
всех целых
положительных
чисел.
- множество
всех целых
положительных
чисел.
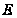 - единичная
группа;
- единичная
группа;
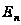 - единичная
матрица размерности
- единичная
матрица размерности
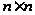 ;
;
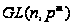 - полная
линейная группа
степени
- полная
линейная группа
степени
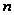 над полем из
над полем из
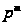 элементов, т.е.
группа всех
невырожденных
линейных
преобразований
элементов, т.е.
группа всех
невырожденных
линейных
преобразований
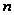 -мерного
линейного
пространства
над полем из
-мерного
линейного
пространства
над полем из
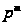 элементов;
элементов;
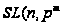 )
- специальная
линейная группа
степени
)
- специальная
линейная группа
степени
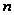 над полем из
над полем из
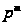 элементов.
элементов.
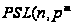 )
- проективная
специальная
линейная группа
степени
)
- проективная
специальная
линейная группа
степени
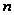 над полем из
над полем из
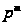 элементов, т.е.
факторгруппа
специальной
линейной группы
по ее центру
элементов, т.е.
факторгруппа
специальной
линейной группы
по ее центру
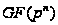 - конечное
поле порядка
- конечное
поле порядка
 .
.
Пусть
 - группа. Тогда:
- группа. Тогда:
 - порядок
группы
- порядок
группы
 ;
;
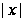 - порядок
элемента
- порядок
элемента
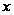 группы
группы
 ;
;
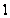 - единичный
элемент и единичная
подгруппа
группы
- единичный
элемент и единичная
подгруппа
группы
 ;
;
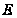 - также
единичная
подгруппа
группы
- также
единичная
подгруппа
группы
 ;
;
 - множество
всех простых
делителей
порядка группы
- множество
всех простых
делителей
порядка группы
 ;
;
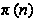 - множество
всех различных
простых делителей
натурального
числа
- множество
всех различных
простых делителей
натурального
числа
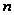 ;
;
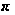 -группа
- группа
-группа
- группа
 ,
для которой
,
для которой
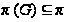 ;
;
 -группа
- группа
-группа
- группа
 ,
для которой
,
для которой
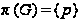 ;
;
Группа
 называется:
называется:
примарной,
если
 ;
;
бипримарной,
если
 .
.
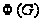 - подгруппа
Фраттини группы
- подгруппа
Фраттини группы
 ,
т.е. пересечение
всех максимальных
подгрупп группы
,
т.е. пересечение
всех максимальных
подгрупп группы
 ;
;
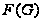 - подгруппа
Фиттинга группы
- подгруппа
Фиттинга группы
 ,
т.е. произведение
всех нормальных
нильпотентных
подгрупп группы
,
т.е. произведение
всех нормальных
нильпотентных
подгрупп группы
 ;
;
 - коммутант
группы
- коммутант
группы
 ,
т.е. подгруппа,
порожденная
коммутаторами
всех элементов
группы
,
т.е. подгруппа,
порожденная
коммутаторами
всех элементов
группы
 ;
;
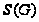 - наибольшая
нормальная
разрешимая
подгруппа
группы
- наибольшая
нормальная
разрешимая
подгруппа
группы
 ;
;
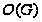 - наибольшая
нормальная
подгруппа
нечетного
порядка группы
- наибольшая
нормальная
подгруппа
нечетного
порядка группы
 ;
;
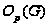 - наибольшая
нормальная
- наибольшая
нормальная
 -подгруппа
группы
-подгруппа
группы
 ;
;
 -
-
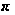 -холловская
подгруппа
группы
-холловская
подгруппа
группы
 ;
;
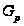 - силовская
- силовская
 -подгруппа
группы
-подгруппа
группы
 ;
;
 - дополнение
к силовской
- дополнение
к силовской
 -подгруппе
в группе
-подгруппе
в группе
 ,
т.е.
,
т.е.
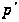 -холловская
подгруппа
группы
-холловская
подгруппа
группы
 ;
;
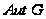 - группа
всех автоморфизмов
группы
- группа
всех автоморфизмов
группы
 ;
;
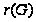 - главный
ранг группы
- главный
ранг группы
 ;
;
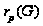 -
-
 -главный
ранг группы
-главный
ранг группы
 ;
;
 -
-
 является максимальной
подгруппой
группы
является максимальной
подгруппой
группы
 ;
;
Пусть
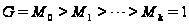 - максимальная
цепь подгрупп,
т.е.
- максимальная
цепь подгрупп,
т.е.
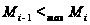 для всех
для всех
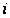 .
Если
.
Если
 разрешима, то
все индексы
максимальной
цепи примарны,
т.е.
разрешима, то
все индексы
максимальной
цепи примарны,
т.е.
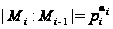 .
Тогда:
.
Тогда:
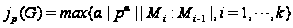
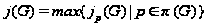 .
.
При
введении обозначений
 и
и
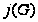 рассматриваются
все максимальные
цепи.
рассматриваются
все максимальные
цепи.
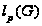 -
-
 -длина
группы
-длина
группы
 ;
;
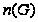 - нильпотентная
длина группы
- нильпотентная
длина группы
 ;
;
