Нильпотентная длина конечных групп с известными добавлениями к максимальным подгруппам
height="29" align="BOTTOM" border="0" />. Поэтому группа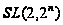 в случае, когда
в случае, когда
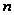 и
и
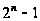 - простые числа,
удовлетворяет
условию теоремы.
- простые числа,
удовлетворяет
условию теоремы.
Проверим,
что группа
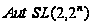 не удовлетворяют
условию теоремы.
Пусть
не удовлетворяют
условию теоремы.
Пусть
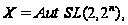
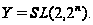
Известно,
что
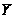 - нормальная
в
- нормальная
в
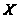 подгруппа, а
подгруппа, а
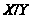 - циклическая
группа порядка
- циклическая
группа порядка
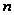 .
Для силовской
.
Для силовской
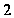 -подгруппы
-подгруппы
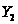 из
из
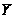 имеем
имеем
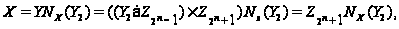
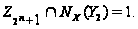
Теперь
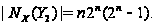
Поскольку
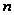 и
и
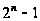 - простые числа,
то в
- простые числа,
то в
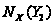 существует
подгруппа
существует
подгруппа
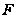 порядка
порядка
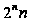 .
Для
.
Для
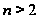 подгруппа
подгруппа
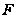
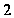 -замкнута,
и внешний автоморфизм
-замкнута,
и внешний автоморфизм
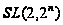 не централизует
силовскую
не централизует
силовскую
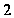 -подгруппу,
поэтому
-подгруппу,
поэтому
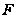 несверхразрешима.
Так как в
несверхразрешима.
Так как в
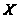 нет нильпотентной
подгруппы
порядка
нет нильпотентной
подгруппы
порядка
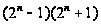 ,
то
,
то
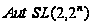 не удовлетворяет
условию теоремы
при
не удовлетворяет
условию теоремы
при
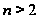 .
Если
.
Если
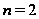 ,
то в
,
то в
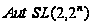 для подгруппы
Шмидта, изоморфной
знакопеременной
группе
для подгруппы
Шмидта, изоморфной
знакопеременной
группе
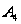 степени
степени
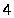 ,
должна найтись
нильпотентная
подгруппа
,
должна найтись
нильпотентная
подгруппа
 порядка, делящегося
на
порядка, делящегося
на
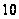 .
Но такой нильпотентной
подгруппы в
.
Но такой нильпотентной
подгруппы в
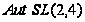 нет.
нет.
Итак,
если
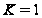 ,
то
,
то
 изоморфна
изоморфна
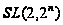 ,
где
,
где
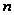 и
и
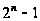 - простые числа.
- простые числа.
Пусть
теперь
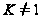 .
Предположим,
что
.
Предположим,
что
 не является
минимальной
нормальной
в
не является
минимальной
нормальной
в
 подгруппой,
и пусть
подгруппой,
и пусть
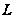 - минимальная
нормальная
в
- минимальная
нормальная
в
 подгруппа,
содержащаяся
в
подгруппа,
содержащаяся
в
 .
По индукции,
.
По индукции,
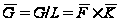 ,
где
,
где
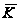 - нильпотентна,
а
- нильпотентна,
а
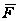 изоморфна
изоморфна
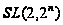 или
или
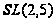 .
Так как
.
Так как
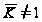 ,
то
,
то
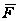 - собственная
в
- собственная
в
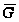 подгруппа, и
для её прообраза
подгруппа, и
для её прообраза
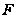 в группе
в группе
 по индукции
получаем, что
по индукции
получаем, что
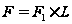 ,
где
,
где
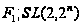 или
или
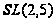 .
Подгруппа
.
Подгруппа
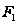 характеристична
в
характеристична
в
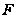 ,
а
,
а
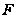 нормальна в
нормальна в
 ,
поэтому
,
поэтому
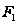 нормальна в
нормальна в
 .
Так как
.
Так как
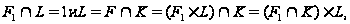 то
то
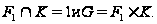
Поскольку
для несверхразрешимой
подгруппы
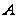 из
из
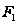 существует
нильпотентная
подгруппа
существует
нильпотентная
подгруппа
 такая, что
такая, что
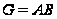 ,
то
,
то
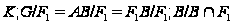
будет нильпотентной подгруппой.
Теперь
рассмотрим
случай, когда
 - минимальная
нормальная
в
- минимальная
нормальная
в
 подгруппа.
Предположим,
что коммутант
подгруппа.
Предположим,
что коммутант
 - собственная
в
- собственная
в
 подгруппа. Так
как
подгруппа. Так
как
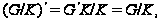 то
то
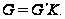
Из
минимальности
 получаем, что
получаем, что
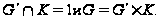 Так
как
Так
как
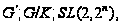
где
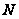 и
и
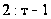 - простые числа,
то в этом случае
теорема доказана.
- простые числа,
то в этом случае
теорема доказана.
Итак,
пусть
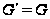 .
Если
.
Если
 - собственная
подгруппа в
своём централизаторе,
то из простоты
- собственная
подгруппа в
своём централизаторе,
то из простоты
 следует, что
следует, что
 содержится
в центре
содержится
в центре
 .
Теперь группа
.
Теперь группа
 изоморфна
изоморфна
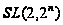 или
или
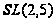 по теореме
VI.25.7 [14].
по теореме
VI.25.7 [14].
Пусть
 самоцентрализуема.
Поскольку
самоцентрализуема.
Поскольку
 разрешима, то
разрешима, то
 -
-
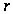 -группа
для некоторого
простого
-группа
для некоторого
простого
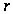 .
Допусти, что
существует
простое
.
Допусти, что
существует
простое
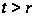 ,
делящее порядок
,
делящее порядок
 ,
и пусть
,
и пусть
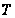 - силовская
- силовская
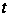 -подгруппа
из
-подгруппа
из
 .
Если подгруппа
.
Если подгруппа
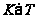 сверхразрешима,
то
сверхразрешима,
то
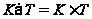 нильпотентна
и
нильпотентна
и
 не самоцентрализуема.
Если
не самоцентрализуема.
Если
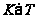 не сверхразрешима,
то по условию
теоремы существует
нильпотентная
подгруппа
не сверхразрешима,
то по условию
теоремы существует
нильпотентная
подгруппа
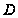 такая, что
такая, что
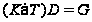 .
Но теперь
.
Но теперь
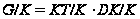
будет
разрешимой
как произведение
двух нильпотентных
подгрупп,
противоречие.
Итак,
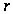 - наибольшее
простое число,
делящее порядок
- наибольшее
простое число,
делящее порядок
 .
.
Допустим,
что
 не содержится
в
не содержится
в

