Нильпотентная длина конечных групп с известными добавлениями к максимальным подгруппам
длина конечных групп с известными добавлениями к максимальным подгруппам" width="17" height="18" align="BOTTOM" border="0" />. Тогда - собственная
в
- собственная
в
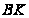 подгруппа и
подгруппа и
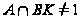 .
Так как
.
Так как
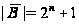 ,
,
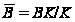 и
и
 -
-
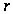 -группа,
то
-группа,
то
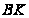 - группа нечётного
порядка. Подгруппа
- группа нечётного
порядка. Подгруппа
 имеет порядок
имеет порядок
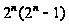 и
и
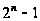 - простое число.
Поэтому
- простое число.
Поэтому
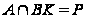 и теперь
и теперь
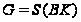 ,
а фактор-группа
,
а фактор-группа
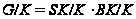
будет разрешимой как произведение двух нильпотентных подгрупп. Противоречие.
Следовательно,
 содержится
в
содержится
в
 и из самоцентрализуемости
и из самоцентрализуемости
 и нильпотентности
и нильпотентности
 получаем, что
получаем, что
 -
-
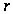 -группа
для наибольшего
простого
-группа
для наибольшего
простого
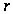 ,
делящего порядок
,
делящего порядок
 .
Из теоремы 2.1
[15] получаем, что
.
Из теоремы 2.1
[15] получаем, что
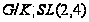 ,
а
,
а
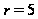 .
Но теперь
.
Но теперь
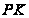 - подгруппа
непримарного
индекса. Поэтому
она сверхразрешима,
а так как её
порядок равен
- подгруппа
непримарного
индекса. Поэтому
она сверхразрешима,
а так как её
порядок равен
 ,
то
,
то
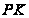 нильпотентна,
и опять
нильпотентна,
и опять
 не самоцентрализуема.
Противоречие.
не самоцентрализуема.
Противоречие.
Теорема доказана полностью.
Рассмотрим доказательство следствия.
Proof. Пусть
 - конечная
неразрешимая
группа, в которой
все подгруппы
непримарного
индекса сверхразрешимы.
Если
- конечная
неразрешимая
группа, в которой
все подгруппы
непримарного
индекса сверхразрешимы.
Если
 - несверхразрешимая
в
- несверхразрешимая
в
 подгруппа, то
подгруппа, то
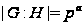 ,
где
,
где
 - простое число.
Теперь
- простое число.
Теперь
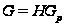 для силовской
для силовской
 -подгруппы
-подгруппы
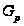 из
из
 ,
т. е. группа
,
т. е. группа
 удовлетворяет
условию теоремы.
Поэтому
удовлетворяет
условию теоремы.
Поэтому
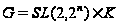 или
или
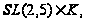
где
 - нильпотентная
группа. Если
- нильпотентная
группа. Если
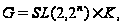
то в
 имеется несверхразрешимая
подгруппа
имеется несверхразрешимая
подгруппа
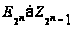 индекса
индекса
 .
Так как этот
индекс должен
быть примарен,
то
.
Так как этот
индекс должен
быть примарен,
то
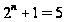 или
или
 ,
поэтому
,
поэтому
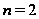 или
или
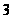 ,
а
,
а
 - либо
- либо
 -группа,
либо
-группа,
либо
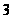 -группа.
Если
-группа.
Если
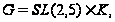
то в
 имеется несверхразрешимая
подгруппа
Шмидта порядка
имеется несверхразрешимая
подгруппа
Шмидта порядка
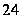 ,
а её индекс
равен
,
а её индекс
равен
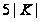 и должен быть
примарен, т. е.
и должен быть
примарен, т. е.
 должна быть
должна быть
 -группой.
Следствие
доказано.
-группой.
Следствие
доказано.
4 ИСПОЛЬЗУЕМЫЕ РЕЗУЛЬТАТЫ
Лемма
4.1. Пусть
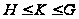 .
Тогда:
.
Тогда:
(1) если
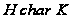 ,
,
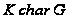 ,
то
,
то
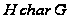 ;
;
(2) если
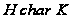 ,
,
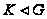 ,
то
,
то
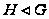 .
.
Следствие
4.2. Если
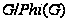 нильпотентна,
то
нильпотентна,
то
 нильпотентна.
нильпотентна.
Теорема
4.3. Пусть
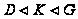 ,
,
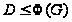 и
и
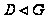 .
Если
.
Если
 нильпотентна,
то
нильпотентна,
то
 нильпотентна.
нильпотентна.
Теорема
4.4. (1) Центр
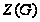 неединичной
нильпотентной
группы
неединичной
нильпотентной
группы
 отличен от
единицы и
отличен от
единицы и
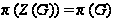 .
.
(2) В нильпотентной группе каждая собственная подгруппа отлична от своего нормализатора.
(3) В
нильпотентной
группе
 пересечение
неединичной
нормальной
подгруппы
пересечение
неединичной
нормальной
подгруппы
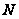 с центром группы
отлично от
единицы и
с центром группы
отлично от
единицы и
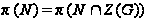 .
.
Лемма
4.5. Пусть
 - нормальная
подгруппа
группы
- нормальная
подгруппа
группы
 .
Тогда:
.
Тогда:
(1) если
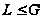 ,
то
,
то и
и
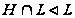 ;
;
(2) если
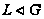 ,
то
,
то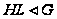 и
и
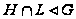 ;
;
(3)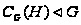 ;
;
(4)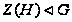 .
.
Теорема 4.6. Группа нильпотентна тогда и только тогда, когда её коммутант содержится в подгруппе Фраттини.
Теорема
4.7. Пусть
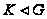 .
Тогда:
.
Тогда:
(1)
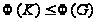 ;
;
(2)
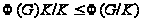 ;
;
(3) если
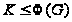 ,
то
,
то
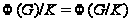 ;
;
(4) если
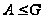 и
и
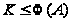 ,
то
,
то
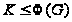 .
.
Лемма
4.8. Тогда и только
тогда подгруппа
 является добавлением
к нормальной
подгруппе
является добавлением
к нормальной
подгруппе
 в группе
в группе
 ,
когда
,
когда
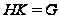 и
и
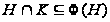 .
.
Следствие
4.9. (1) Если
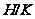 - главный фактор
конечной группы
- главный фактор
конечной группы
 ,
то
,
то
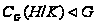 и
и

(2) Если
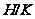 - главный фактор
порядка
- главный фактор
порядка
 конечной группы
конечной группы
 ,
то
,
то
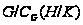 - циклическая
группа порядка,
делящего
- циклическая
группа порядка,
делящего
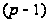 .
.
Теорема
4.10. (1) Если существует
натуральное
число
 такое, что
такое, что
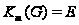 ,
то группа
,
то группа

