Нильпотентная длина конечных групп с известными добавлениями к максимальным подгруппам

групп с известными добавлениями к максимальным подгруппам" width="42" height="22" align="BOTTOM" border="0" />.

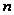Определение. Нильпотентной длиной разрешимой группы называют наименьшее , для которого 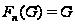. Нильпотентную длину разрешимой группы обозначают через .

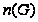На основе подгруппы Фиттинга вводится следующая

Теорема А. Подгруппа Фиттинга совпадает с пересечением централизаторов главных факторов группы.

Также рассматривается доказательство теоремы К. Дёрка.

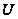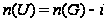Теорема B. Если - максимальная подгруппа разрешимой группы , то , где .

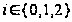Доказана теорема Монахова В.С.

Определение. Подгруппа группы называется максимальной подгруппой, если не содержится ни в какой другой подгруппе, отличной от .

Определение. Подгруппой Фраттини группы называется пересечение всех ее максимальных подгрупп. Подгруппа Фраттини группы обозначается через .

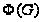Теорема C. (1) В разрешимой неединичной группе подгруппа Фраттини совпадает с пересечением максимальных подгрупп, не содержащих подгруппу Фиттинга.

(2) В разрешимой ненильпотентной группе пересечение максимальных подгрупп, содержащих подгруппу Фиттинга, метанильпотентно.

Во второй главе "-длина -разрешимой группы" даны следующие определения.

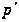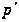Определение. Пусть - простое число. Назовем группу -группой, если ее порядок не делится на и, как обычно, -группой, если её порядок равен степени числа . Конечную группу будем называть -разрешимой, если каждый из её композиционных факторов является либо -группой, либо -группой. Таким образом, группа разрешима в обычном смысле тогда и только тогда, когда она -разрешима для всех простых . Ясно, что группа -разрешима тогда и только тогда, когда она обладает нормальным рядом

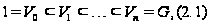
в котором каждая факторгруппа 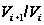является либо -группой, либо 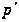-группой.

Определение. Наименьшее целое число , для которого 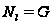, мы назовем -длинной группы и обозначим его , или, если необходимо, .

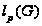-длину -разрешимой группы можно также определить как наименьшее число -факторов, встречающихся в каком либо ряде вида (2.1), поскольку минимум достигается для верхнего -ряда

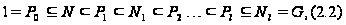
Доказывается

Теорема D. Если - -разрешимая группа, где - нечетное простое число, то

(i)

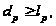
(ii) если не является простым числом Ферма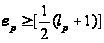, и , если - простое число Ферма. Кроме того, эти оценки нельзя улучшить.

В главе "Группа с нильпотентными добавлениями к подгруппам" доказана важная теорема.

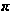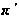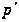Определение. Группа называется -сверхразрешимой, если ее главные факторы либо -группы, либо имеют простые порядки. -Сверхразрешимой называют группу, у которой факторы главного ряда либо имеют порядок , либо являются -группами. Группа, у которой все факторы главного ряда имеют простые порядки, называется сверхразрешимой.

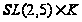Теорема E. Конечная неразрешимая группа с нильпотентными добавлениями к несверхразрешимым подгруппам изоморфна или , где - нильпотентная группа, а 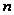и 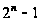- простые числа.

Также доказано следствие из этой теоремы.

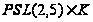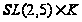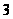Следствие. Конечная неразрешимая группа, в которой все подгруппы непримарного индекса сверхразрешимы, изоморфна или , где - -группа, либо , где - -группа.

1 ПОДГРУППА ФИТТИНГА И ЕЁ СВОЙСТВА

Произведение всех нормальных нильпотентных подгрупп группы называют подгруппой Фиттинга группы и обозначают через 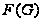. Множество простых делителей порядка группы обозначается через 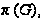а наибольшую нормальную -подгруппу группы - через .

Лемма 1.1. (1) 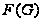- наибольшая нормальная нильпотентная подгруппа группы ;

(2) ;

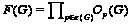(3) .

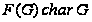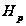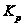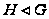Proof. (1) Пусть и - нильпотентные нормальные подгруппы группы и пусть и - силовские -подгруппы из и . Так как , а , то 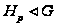по лемме 4.1, с. 35. Аналогично, 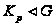, поэтому . Ясно, - -группа. Покажем, что она силовская в 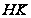. Для этого вычислим ее индекс:

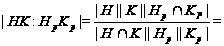
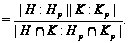
Так как числитель не делится на , то - силовская -подгруппа группы 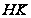. Итак, произведение двух нормальных нильпотентных подгрупп есть нормальная нильпотентная подгруппа. Поэтому 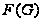- наибольшая нормальная нильпотентная подгруппа группы .

(2) Ясно, что 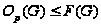для