Нильпотентная длина конечных групп с известными добавлениями к максимальным подгруппам
всех ,
поэтому
,
поэтому
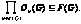
Обратно,
если
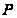 - силовская
- силовская
 -подгруппа
группы
-подгруппа
группы
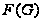 ,
то
,
то
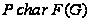 и
и
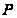 нормальна в
нормальна в
 ,
поэтому
,
поэтому
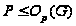 и
и
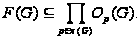
(3) Если
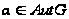 ,
то
,
то
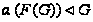 и
и
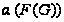 нильпотентна,
поэтому
нильпотентна,
поэтому
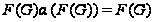 по (1) и
по (1) и
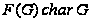 .
.
Лемма
1.2. (1)
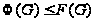 ;
если
;
если
 разрешима и
разрешима и
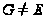 ,
то
,
то
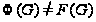 ;
;
(2)
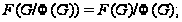
(3) если
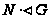 ,
то
,
то
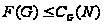 ;
если, кроме
того,
;
если, кроме
того,
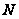 абелева, то
абелева, то
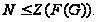
Proof. (1) Поскольку
подгруппа
Фраттини
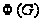 - нильпотентная
нормальная
подгруппа
группы
- нильпотентная
нормальная
подгруппа
группы
 ,
то
,
то
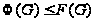 .
Пусть
.
Пусть
 - разрешимая
неединичная
группа. Тогда
- разрешимая
неединичная
группа. Тогда
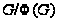 разрешима и
неединична.
Пусть
разрешима и
неединична.
Пусть
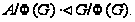
Так
как
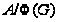 -
-
 -группа
для некоторого
простого
-группа
для некоторого
простого
 ,
то по следствию
4.2, с. 35, подгруппа
,
то по следствию
4.2, с. 35, подгруппа
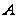 нильпотентна
и
нильпотентна
и
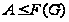 .
Следовательно,
.
Следовательно,
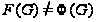 .
.
(2) Если
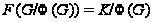 ,
то
,
то
 - нильпотентная
нормальная
в
- нильпотентная
нормальная
в
 подгруппа по
теореме 4.3, с. 35,
поэтому
подгруппа по
теореме 4.3, с. 35,
поэтому
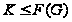 и
и
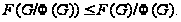
Обратное включение следует из определения подгруппы Фиттинга.
(3) Для
минимальной
нормальной
подгруппы
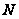 либо
либо
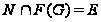 ,
либо
,
либо
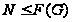 .
Если
.
Если
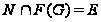 ,
то
,
то
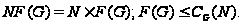
Если
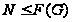 ,
то
,
то
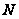 - элементарная
абелева
- элементарная
абелева
 -группа
для некоторого
простого
-группа
для некоторого
простого
 .
Так как
.
Так как
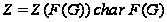 ,
то
,
то
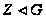 .
С другой стороны,
.
С другой стороны,
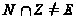 по теореме 4.4,
с. 35, поэтому
по теореме 4.4,
с. 35, поэтому
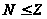 .
.
Теорема
1.3.
 для любого
для любого
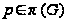 .
В частности,
если
.
В частности,
если
 разрешима, то
разрешима, то
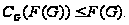
Proof. Пусть
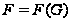 ,
,
 .
Так как
.
Так как
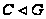 по лемме 4.5, с. 35,
то
по лемме 4.5, с. 35,
то
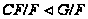 .
Предположим,
что
.
Предположим,
что
 для некоторого
для некоторого
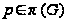 и пусть
и пусть
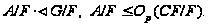
Ясно,
что
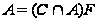 и
и
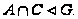 Пусть
Пусть
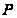 - силовская
- силовская
 -подгруппа
группы
-подгруппа
группы
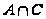 .
Так как
.
Так как
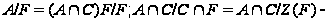
 -группа,
то
-группа,
то
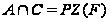 ,
а поскольку
,
а поскольку
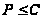 ,
то
,
то
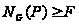 и
и
 .
Теперь,
.
Теперь,
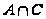 - нильпотентная
нормальная
подгруппа
группы
- нильпотентная
нормальная
подгруппа
группы
 и
и
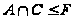 .
Таким образом,
.
Таким образом,
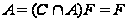 и первое утверждение
доказано. Если
и первое утверждение
доказано. Если
 разрешима, то
разрешима, то
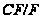 разрешима,
поэтому
разрешима,
поэтому
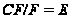 и
и
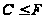 .
.
Говорят,
что подгруппа
 группы
группы
 дополняема
в
дополняема
в
 ,
если существует
такая подгруппа
,
если существует
такая подгруппа
 ,
что
,
что
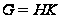 и
и
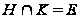 .
В этом случае
подгруппу
.
В этом случае
подгруппу
 называют дополнением
к подгруппе
называют дополнением
к подгруппе
 в группе
в группе
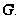
Теорема
1.4. Если
 - нильпотентная
нормальная
подгруппа
группы
- нильпотентная
нормальная
подгруппа
группы
 и
и
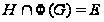 ,
то
,
то
 дополняема
в
дополняема
в
 .
.
Proof. По
условию
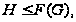 а по теореме
4.6, с. 35, коммутант
а по теореме
4.6, с. 35, коммутант
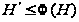 .
По теореме 4.7,
с. 35, подгруппа
Фраттини
.
По теореме 4.7,
с. 35, подгруппа
Фраттини
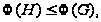 а по условию
а по условию
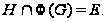 Поэтому
Поэтому
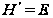 и
и
 абелева. Пусть
абелева. Пусть
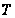 - добавление
к
- добавление
к
 в
в
 .
По лемме 4.8, с. 35,
.
По лемме 4.8, с. 35,
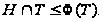 Поскольку
Поскольку
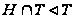 и
и
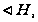 то
то
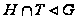 и по теореме
4.7, с. 35,
и по теореме
4.7, с. 35,
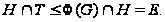
Следовательно,
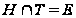 и
и
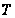 - дополнение
к
- дополнение
к

