Нильпотентная длина конечных групп с известными добавлениями к максимальным подгруппам
длина конечных групп с известными добавлениями к максимальным подгруппам" width="58" height="22" align="BOTTOM" border="0" /> нильпотентна, то по теореме 4.3, с. 35, подгруппа нильпотентна
и
нильпотентна
и
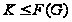 .
Но теперь
.
Но теперь

противоречие.
Поэтому допущение
неверно и
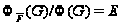 ,
т.е.
,
т.е.
 .
.
(2) Пусть
 - разрешимая
ненильпотентная
группа. Ясно,
что
- разрешимая
ненильпотентная
группа. Ясно,
что
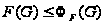
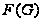 и
и
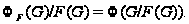
Поэтому
подгруппа
 метанильпотентна.
метанильпотентна.
Пример
1.16. В неразрешимой
группе
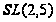 центр, подгруппа
Фраттини и
подгруппа
Фиттинга совпадают
и имеют порядок
центр, подгруппа
Фраттини и
подгруппа
Фиттинга совпадают
и имеют порядок
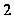 .
Поэтому в группе
.
Поэтому в группе
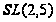 нет максимальных
подгрупп, не
содержащих
подгруппу
Фиттинга.
нет максимальных
подгрупп, не
содержащих
подгруппу
Фиттинга.
Следовательно, утверждение (1) теоремы 1.15 в неразрешимых группах нарушается.
2
 -ДЛИНА
-ДЛИНА
 -РАЗРЕШИМОЙ
ГРУППЫ
-РАЗРЕШИМОЙ
ГРУППЫ
Пусть
 - простое число.
Назовем группу
- простое число.
Назовем группу
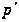 -группой,
если ее порядок
не делится на
-группой,
если ее порядок
не делится на
 и, как обычно,
и, как обычно,
 -группой,
если её порядок
равен степени
числа
-группой,
если её порядок
равен степени
числа
 .
Конечную группу
.
Конечную группу
 будем называть
будем называть
 -разрешимой,
если каждый
из её композиционных
факторов является
либо
-разрешимой,
если каждый
из её композиционных
факторов является
либо
 -группой,
либо
-группой,
либо
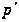 -группой.
Таким образом,
группа
-группой.
Таким образом,
группа
 разрешима в
обычном смысле
тогда и только
тогда, когда
она
разрешима в
обычном смысле
тогда и только
тогда, когда
она
 -разрешима
для всех простых
-разрешима
для всех простых
 .
Ясно, что группа
.
Ясно, что группа

 -разрешима
тогда и только
тогда, когда
она обладает
нормальным
рядом
-разрешима
тогда и только
тогда, когда
она обладает
нормальным
рядом
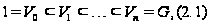
в котором
каждая факторгруппа
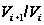 является либо
является либо
 -группой,
либо
-группой,
либо
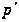 -группой.
Поэтому для
такой группы
мы можем индуктивно
определить
верхний
-группой.
Поэтому для
такой группы
мы можем индуктивно
определить
верхний
 -ряд.
-ряд.
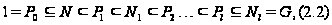
потребовав,
чтобы
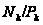 была наибольшей
нормальной
была наибольшей
нормальной
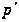 -подгруппой
в
-подгруппой
в
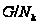 ,
а
,
а
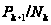 - наибольшей
нормальной
- наибольшей
нормальной
 -подгруппой
в
-подгруппой
в
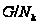 .
.
Наименьшее
целое число
 ,
для которого
,
для которого
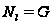 ,
мы назовем
,
мы назовем
 -длинной
группы
-длинной
группы
 и обозначим
его
и обозначим
его
 ,
или, если необходимо,
,
или, если необходимо,
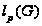 .
.
 -длину
-длину
 -разрешимой
группы можно
также определить
как наименьшее
число
-разрешимой
группы можно
также определить
как наименьшее
число
 -факторов,
встречающихся
в каком либо
ряде вида (2.1),
поскольку
минимум достигается
для верхнего
-факторов,
встречающихся
в каком либо
ряде вида (2.1),
поскольку
минимум достигается
для верхнего
 -ряда
(2.2). Подгруппы
-ряда
(2.2). Подгруппы
 и
и
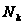 ,
очевидно,
характеристичны
в
,
очевидно,
характеристичны
в
 ,
и
,
и
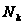 содержит все
нормальные
подгруппы
группы
содержит все
нормальные
подгруппы
группы
 с
с
 -длинной,
не превосходящей
числа
-длинной,
не превосходящей
числа
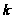 .
Заметим также,
что
.
Заметим также,
что
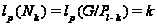
для
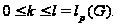
Подгруппы
и факторгруппы
 -разрешимой
группы
-разрешимой
группы
 также
также
 -разрешимы,
и их длина не
превышает
-разрешимы,
и их длина не
превышает
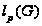 .
Если группы
.
Если группы
 и
и
 обе
обе
 -разрешимы,
то таково же
их прямое
произведение
-разрешимы,
то таково же
их прямое
произведение
 и
и
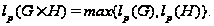
Пусть
 -
-
 -разрешимая
группа и
-разрешимая
группа и
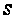 -
ее силовская
-
ее силовская
 -подгруппа.
Разумно предположить,
что чем больше
-подгруппа.
Разумно предположить,
что чем больше
 -длинна
-длинна
 группы
группы
 ,
тем большей
должна быть
сложность
силовской
подгруппы
,
тем большей
должна быть
сложность
силовской
подгруппы
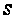 .
Придадим точный
смысл этому
утверждению
и докажем его
несколькими
способами,
избирая различные
критерии сложности
.
Придадим точный
смысл этому
утверждению
и докажем его
несколькими
способами,
избирая различные
критерии сложности
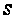 .
Наиболее естественные
из этих критериев,
силовские
.
Наиболее естественные
из этих критериев,
силовские
 -инварианты
группы
-инварианты
группы
 ,
таковы:
,
таковы:
(i)
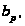 где
где
 - порядок
- порядок
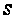 ,
,
(ii)
 - класс нильпотентности
- класс нильпотентности
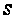 ,
т.е. длина (верхнего
или) нижнего
центрального
ряда
,
т.е. длина (верхнего
или) нижнего
центрального
ряда
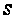 ,
,
(iii)
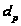 - длина ряда
коммутантов
- длина ряда
коммутантов
 ,
,
(iv)
 где
где
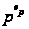 - экспонента
- экспонента
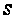 ,
т.е.
,
т.е.
наибольший
из порядков
элементов
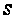 .
Экспонента
самой группы
.
Экспонента
самой группы
 ,
т.е. наименьшее
общее кратное
порядков ее
элементов,
равна поэтому
,
т.е. наименьшее
общее кратное
порядков ее
элементов,
равна поэтому
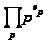 .
Очевидно, равенство
нулю любого
из инвариантов
.
Очевидно, равенство
нулю любого
из инвариантов
 или
или
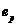 равносильно
тому, что
равносильно
тому, что
 является
является
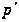 -группой.
-группой.
В основных
теоремах ограничимся
случаем нечетных
простых чисел
 ,
и даже тогда
результаты
будут несколько
различнми, в
зависимости
от того, является
ли
,
и даже тогда
результаты
будут несколько
различнми, в
зависимости
от того, является
ли
 простым числом
Ферма вида
простым числом
Ферма вида
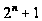 или нет.
или нет.
Справедлива следующая теорема.
Теорема
2.1. Если
 -
-
 -разрешимая
группа, где
-разрешимая
группа, где
 - нечетное простое
число, то
- нечетное простое
число, то
(i)
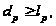
(ii)
 если
если
 не является
простым числом
Ферма, и
не является
простым числом
Ферма, и
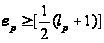 ,
если
,
если
 - простое число
Ферма. Кроме
того, эти оценки
нельзя улучшить.
- простое число
Ферма. Кроме
того, эти оценки
нельзя улучшить.
Мы
установим также
неравенства,
связывающие
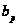 c
c

