Нильпотентная длина конечных групп с известными добавлениями к максимальным подгруппам
максимальным подгруппам" width="17" height="26" align="BOTTOM" border="0" /> и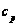 с
с
 ,
но здесь наши
результаты
будут неулучшаемы
только для
простых чисел,
не являющихся
простыми числами
Ферма. Все эти
результаты
тривиальны
для
,
но здесь наши
результаты
будут неулучшаемы
только для
простых чисел,
не являющихся
простыми числами
Ферма. Все эти
результаты
тривиальны
для
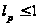 ,
и мы докажем
их индукцией
по
,
и мы докажем
их индукцией
по
 .
Предположим,
что
.
Предположим,
что
 и что
и что
 ,
как всегда
обладает верхним
,
как всегда
обладает верхним
 -рядом
(2.2). Пусть
-рядом
(2.2). Пусть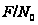 подгруппа
Фраттини
подгруппа
Фраттини
 -группы
-группы
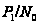 .
Всякий элемент
группы
.
Всякий элемент
группы
 индуцирует
внутренний
автоморфизм
группы
индуцирует
внутренний
автоморфизм
группы
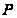 и, следовательно,
группы
и, следовательно,
группы
 .
Но, как извесно,
.
Но, как извесно,
 является элементарной
абелевой
является элементарной
абелевой
 -группой;
поэтому ее
можно отождествить
с аддитивной
группой векторного
пространства
над простым
полем характеристики
-группой;
поэтому ее
можно отождествить
с аддитивной
группой векторного
пространства
над простым
полем характеристики
 ,
а ее автоморфизм
- с линейными
преобразованиями
этого пространства.
Автоморфизмы
группы
,
а ее автоморфизм
- с линейными
преобразованиями
этого пространства.
Автоморфизмы
группы
 ,
индуцированные
элементами
,
индуцированные
элементами
 ,
образуют поэтому
линейную группу
над полем
характеристики
,
образуют поэтому
линейную группу
над полем
характеристики
 .
Эта группа,
очевидно, является
гомоморфным
образом группы
.
Эта группа,
очевидно, является
гомоморфным
образом группы
 ,
и мы покажем,
что в действительности
она изоморфна
группе
,
и мы покажем,
что в действительности
она изоморфна
группе
 ,
и поэтому является
,
и поэтому является
 -разрешимой
группой, не
содержащей
нормальной
подгруппы,
отличной от
единицы.
-разрешимой
группой, не
содержащей
нормальной
подгруппы,
отличной от
единицы.
Теорема
2.2. Пусть
 - разрешимая
линейная группа
над полем
характеристики
- разрешимая
линейная группа
над полем
характеристики
 ,
не содержащая
неединичную
нормальную
,
не содержащая
неединичную
нормальную
 -подгруппу.
Пусть
-подгруппу.
Пусть
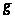 - элемент порядка
- элемент порядка
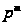 в
в
 .
Тогда минимальное
уравнение для
.
Тогда минимальное
уравнение для
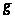 имеет вид
имеет вид
 .
.
Число
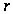 удовлетворяет
следующему
условию. Пусть
удовлетворяет
следующему
условию. Пусть
 наименьшее
целое число
(если оно существует),
для которого
наименьшее
целое число
(если оно существует),
для которого
 является степенью
простого числа
является степенью
простого числа
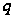 со свойством
со свойством
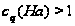 .
Если
.
Если
 не существует,
то
не существует,
то
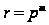 ;
в противном
случае
;
в противном
случае

Этот
результат,
дополненный
более детальными
сведениями
об элементах
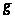 ,
для которых
,
для которых
 ,
будет ключом
к доказательству
теоремы А. Надо
заметить, что
неравенство
,
будет ключом
к доказательству
теоремы А. Надо
заметить, что
неравенство
 может выполняться
только тогда,
когда
может выполняться
только тогда,
когда
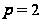 или когда
или когда
 - простое число
Ферма. Теорема
В и подобные
ей теоремы
доказываются
в основном
прямым определением
наименьшей
группы, удовлетворяющей
этим условиям,
и прямым вычислением.
При этом играет
важную роль
следующая
теорема, интересная
сама по себе.
- простое число
Ферма. Теорема
В и подобные
ей теоремы
доказываются
в основном
прямым определением
наименьшей
группы, удовлетворяющей
этим условиям,
и прямым вычислением.
При этом играет
важную роль
следующая
теорема, интересная
сама по себе.
Теорема
2.3. Пусть
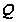 - некоторая
- некоторая
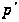 -группа,
на которую
действует
-группа,
на которую
действует
 -группа
-группа
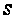 ,
причем некоторый
элемент
,
причем некоторый
элемент
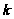 группы
группы
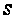 действует
нетривиально
на
действует
нетривиально
на
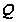 ,
но тривиально
на каждую истинную
,
но тривиально
на каждую истинную
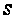 -инвариантную
подгруппу
группы
-инвариантную
подгруппу
группы
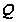 .
Тогда существует
такое простое
число
.
Тогда существует
такое простое
число
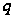 ,
что
,
что
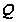 является либо
элементарной
абелевой
является либо
элементарной
абелевой
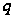 -группой,
либо
-группой,
либо
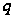 -группой
класса нильпотентности
2, у которой центр
и коммутант
совпадают,
факторгруппа
по коммутанту
-группой
класса нильпотентности
2, у которой центр
и коммутант
совпадают,
факторгруппа
по коммутанту
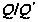 - элементарная
абелева группа
и представление
- элементарная
абелева группа
и представление
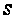 на
на
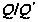 неприводимо.
неприводимо.
Следует
отметить, что
если
 - разрешимая
группа, то
ограничитель
- разрешимая
группа, то
ограничитель
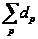 влечет ограниченность
длины ряда
коммутантов
влечет ограниченность
длины ряда
коммутантов
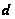 группы
группы
 .
.
Пусть
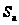 означает следующее
утверждение:
означает следующее
утверждение:
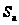 :
для каждого
положительного
целого числа
:
для каждого
положительного
целого числа
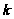 существует
такое целое
число
существует
такое целое
число
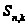 ,
что всякая
разрешимая
группа экспоненты
,
что всякая
разрешимая
группа экспоненты
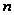 ,
порождаемая
,
порождаемая
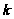 элементами,
имеет порядок
не больше
элементами,
имеет порядок
не больше
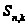 .
.
Теорема
2.4.
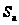 истинно, если
истинно, если
 истинно для
всех степеней
простых чисел
истинно для
всех степеней
простых чисел
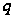 ,
делящих
,
делящих
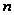 .
.
В частности,
так как известно,
что
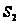 ,
,
 и
и
 истинны, то
истинны
истинны, то
истинны
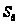 и
и
 .
В этих случаях,
как и всегда,
когда
.
В этих случаях,
как и всегда,
когда
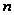 делится только
на два простых
числа, мы можем
слово "разрешимая"
заменить в
формулировке
делится только
на два простых
числа, мы можем
слово "разрешимая"
заменить в
формулировке
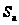 словом "конечная".
Если
словом "конечная".
Если
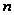 - число, свободное
от квадратов,
мы даже можем
вычислить
- число, свободное
от квадратов,
мы даже можем
вычислить
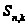 ,
когда
,
когда
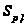 извесны для
всех простых
извесны для
всех простых
 ,
делящих
,
делящих
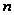 ,
и всех
,
и всех
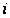 .
Так, порядок
наибольшей
конечной
.
Так, порядок
наибольшей
конечной
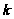 -порожденной
группы экспоненты
6 дается формулой
-порожденной
группы экспоненты
6 дается формулой
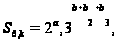 где
где
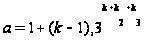 и
и

Пусть
требуется
доказать индукцией
по порядку
группы
 неравенство
неравенство

Здесь
 и
и
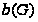 - числовые
инварианты,
определеннные
для некоторого
класса конечных
групп, который
мы предпологаем
замкнутым. Мы
предпологаем,
что (2.3) выполняется
для достаточно
малых
- числовые
инварианты,
определеннные
для некоторого
класса конечных
групп, который
мы предпологаем
замкнутым. Мы
предпологаем,
что (2.3) выполняется
для достаточно
малых
 ,
следовательно
и для
,
следовательно
и для
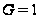 ,
и, кроме того,
что:
,
и, кроме того,
что:
(I) если
 - подгруппа
- подгруппа
 ,
то
,
то
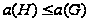 ;
;
(II)
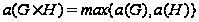 ;
;
(III) если
 - факторгруппа
- факторгруппа
 ,
то
,
то
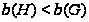 .
.
Тогда справедлива
Лемма
2.5. В доказательстве
неравенства
(2.3) индукцией
по порядку
группы
 можно предположить,
что
можно предположить,
что
 обладает только
одной минимальной
нормальной
подгруппой.
обладает только
одной минимальной
нормальной
подгруппой.
В самом
деле, если
 обладает двумя
минимальными
нормальными
подгруппами
обладает двумя
минимальными
нормальными
подгруппами
 и
и
 ,
мы получим,
,
мы получим,
