Метод векторів та його застосування
що й операція додавання чисел. Тому часто при перетворенні сум векторів діємо так само, як і при перетворенні числових виразів: ( +
+ )+
)+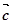 =
= +(
+( +
+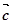 )=(
)=( +
+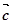 )+
)+ =
= (
(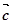 +
+ ).
).
Сума
більшої кількості векторів знаходиться за правилом многокутника.
Щоб знайти суму n векторів 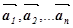 (мал. 9), потрібно з
довільної точки O відкласти вектор
(мал. 9), потрібно з
довільної точки O відкласти вектор 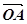 =
=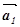 , з його кінця – вектор
, з його кінця – вектор 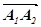 =
=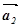 ,…,
,…,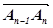 =
=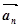 (початок кожного
наступного вектора-доданка є кінцем попереднього). Вектор
(початок кожного
наступного вектора-доданка є кінцем попереднього). Вектор 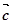 =
=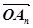 буде сумою даних векторів.
буде сумою даних векторів.
Віднімання векторів
Операція віднімання векторів вводиться як протилежна до додавання.
Означення. Різницею векторів  і
і  називається такий вектор
називається такий вектор 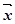 , який в сумі з вектором
, який в сумі з вектором  дає вектор
дає вектор  :
:  -
- =
=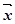 якщо
якщо  +
+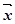 =
= . /1/
. /1/
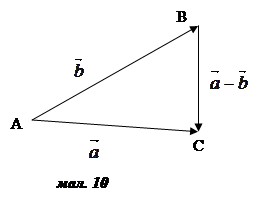
Доведемо, що вектор 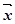 існує і притому
єдиний. Припустимо, що вектор
існує і притому
єдиний. Припустимо, що вектор 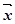 існує. Тоді, додавши до обох
частин рівності вектор (-
існує. Тоді, додавши до обох
частин рівності вектор (- ) і користуючись властивостями
суми векторів, маємо: (-
) і користуючись властивостями
суми векторів, маємо: (- )+
)+ +
+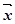 =(-
=(- )+
)+ . /2/
. /2/
Отже,
якщо вектор 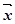 існує, то він визначається попередньою рівністю /2/, а тому єдиний. Дійсно,
підставивши /2/ в /1/, одержимо правильну
рівність:
існує, то він визначається попередньою рівністю /2/, а тому єдиний. Дійсно,
підставивши /2/ в /1/, одержимо правильну
рівність:  +
+ +(-
+(- )=
)= .
.
Отже,
вектор, який визначається формулою /2/, є різницею векторів  і
і  :
:  -
- =
= +(-
+(- )=
)=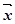 . За правилом трикутника
. За правилом трикутника 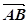 +
+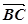 =
=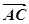 . Звідси
. Звідси
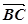 =
=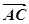 -
-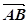 (мал. 10).
(мал. 10).
Отже,
для побудови різниці векторів  і
і  досить відкласти
ці вектори від спільного початку (
досить відкласти
ці вектори від спільного початку (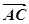 =
= ,
,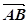 =
= ) і провести вектор
) і провести вектор 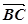 від кінця B
вектора-від’ємника до кінця C вектора-зменшуваного;
цей вектор і є шуканою різницею
від кінця B
вектора-від’ємника до кінця C вектора-зменшуваного;
цей вектор і є шуканою різницею  -
- :
: 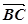 =
= -
- .
.
Множення вектора на число
Означення.
Добутком вектора  на дійсне число α називається
вектор
на дійсне число α називається
вектор 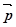 , який задовольняє такі умови:
, який задовольняє такі умови:
1) 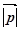 =
=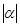 *
*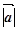 ;
;
2) 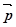

 , якщо α
>0, і
, якщо α
>0, і 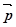
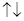
 , якщо α <0.
, якщо α <0.
Такий
вектор позначається 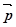 = α
= α  .
.
Операція добутку вектора на число має такі властивості.
Властивість
1.
α*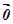 =0*
=0* =
=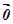 для будь-якого дійсного
числа α і будь-якого вектора
для будь-якого дійсного
числа α і будь-якого вектора  . Ця властивість випливає
з умови 1) означення.
. Ця властивість випливає
з умови 1) означення.
Властивість
2.
Для будь-якого вектора  1*
1* =
= ; -1*
; -1* =-
=- . Ця властивість
випливає безпосередньо з означення.
. Ця властивість
випливає безпосередньо з означення.
Властивість
3.
Для будь-якого вектора  і будь-яких дійсних чисел α і β:
α(β
і будь-яких дійсних чисел α і β:
α(β )=(αβ)
)=(αβ)  .
.
Доведення. Нехай
α(β )=
)=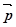 , (αβ)
, (αβ)  =
=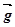 . Доведемо, що
. Доведемо, що 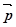 =
=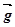 . Маємо:
. Маємо:
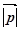 =
=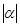 *
*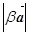 =
=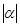 *
*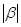 *
*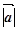 ,
,
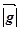 =
=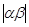 *
*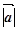 =
=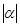 *
*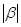 *
*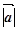 .
.
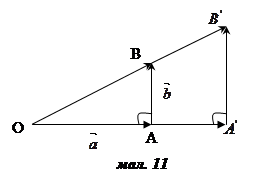
Отже,
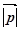 =
=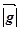 . Покажемо, що
. Покажемо, що 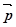

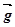 .
Якщо α і β одного знаку, то вектор
.
Якщо α і β одного знаку, то вектор 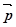 однаково
напрямлений з
однаково
напрямлений з  і
і 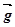 однаково напрямлений з
однаково напрямлений з  .Отже,
.Отже, 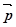

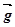 .
У випадку коли числа α і β протилежних знаків,
.
У випадку коли числа α і β протилежних знаків, 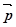
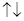
 ,
, 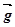
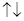
 . Отже, також
. Отже, також 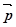

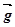 ,
що й треба було довести.
,
що й треба було довести.
Властивість
4.
Операція множення вектора на число дистрибутивна відносно додавання векторів,
тобто α( +
+ )=α
)=α +α
+α , для
, для 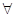
 ,
, і α
і α  R.
R.
Доведення. Нехай α > 0. Відкладемо
вектори 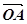 =
= ,
, 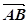 =
= ,
, 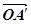 =α
=α ,
, 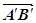 =α
=α  (мал. 11). Тоді
(мал. 11). Тоді  +
+ =
=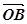 , α
, α +α
+α =
=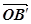 . Покажемо, що
. Покажемо, що 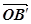 =α
=α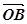 . Оскільки вектори
. Оскільки вектори  і α
і α  ,
,  і α
і α відповідно однаково напрямлені, то відповідні кути
A і
відповідно однаково напрямлені, то відповідні кути
A і 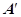 у трикутників OAB і
у трикутників OAB і 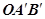 рівні (як кути утворені при перетині двох паралельних
прямих третьою). Крім того, сторони цих трикутників, що прилягають до рівних
кутів, пропорційні:
рівні (як кути утворені при перетині двох паралельних
прямих третьою). Крім того, сторони цих трикутників, що прилягають до рівних
кутів, пропорційні: 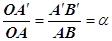 . Тому
. Тому  OAB ~
OAB ~ 
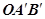 . Звідси випливає, що OAB=
. Звідси випливає, що OAB=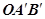 , а це означає, що промені OB і
, а це означає, що промені OB і 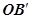 збігаються, тобто
збігаються, тобто 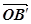

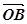 . Крім того
. Крім того 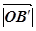 =α*
=α*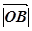 =
=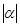 *
*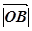 . Тому
. Тому 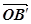 =α*
=α*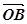 .
.
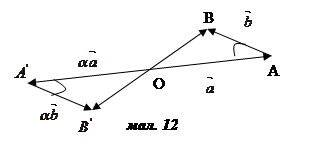
Аналогічно розглядається випадок, коли α <0 (мал. 12).
Випадок
α = 0 тривіальний. Отже, α ( +
+ ) = α
) = α +α
+α .
.
Властивість
5.
Операція множення вектора на число дистрибутивна відносно додавання чисел,
тобто (α+β) =α
=α +β
+β ,
, 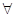
 і α, β
і α, β  R.
R.
Доведення. Розглянемо два можливих випадки: αβ >0 і αβ <0 (випадок αβ=0 не викликає труднощів).
1.
Нехай αβ >0, тобто числа α і β одного знаку. Тоді вектори
(α+β) і α
і α +β
+β однаково
напрямлені. Крім того,
однаково
напрямлені. Крім того,
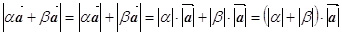 ;
;
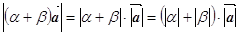 .
.
Отже,
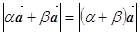 і вектори (α+β)
і вектори (α+β) та α
та α +β
+β рівні.
рівні.
2.
Нехай αβ <0, тобто числа α і β різних знаків. Якщо α = -β,
то (α+β) =(-β+β)
=(-β+β) =0
=0 =0; α
=0; α +β
+β = -β
= -β + β
+ β =0, отже, властивість
справджується.
=0, отже, властивість
справджується.
Якщо
α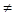 -β, тоді –α, α+β або
–β, α+β одного знаку. Нехай, наприклад, -α, α+β
одного знаку. Тоді за доведеним (-α)
-β, тоді –α, α+β або
–β, α+β одного знаку. Нехай, наприклад, -α, α+β
одного знаку. Тоді за доведеним (-α) + (α+β)
+ (α+β) =(-α+α+β)
=(-α+α+β) =β
=β
 (α+β)
(α+β) = α
= α +β
+β , що і треба було довести.
, що і треба було довести.
2. Колінеарність векторів
Означення. Два ненульових вектори  і
і  називається колінеарними,
якщо відповідні їм напрямлені відрізки паралельні або лежать на одній
прямій.
називається колінеарними,
якщо відповідні їм напрямлені відрізки паралельні або лежать на одній
прямій.
Позначення:  ||
|| (мал. 13).
(мал. 13).
Очевидно, колінеарні вектори або однаково напрямлені (мал. 13а), або протилежно напрямлені (мал. 12b). Нульовий вектор вважається колінеарним будь-якому вектору. Тому, якщо відомо, що деякі два вектори неколінеарні, то жоден з них не є нульовим вектором.
Теорема. (перша ознака
колінеарності двох векторів). Два ненульових вектори  і
і  колінеарні тоді і тільки
тоді, коли існує деяке число α таке, що
колінеарні тоді і тільки
тоді, коли існує деяке число α таке, що  =α
=α . /1/
. /1/
Доведення.
1.
Необхідність. Нехай  ||
|| . Тоді або
. Тоді або 

 , або
, або 
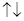
 . Якщо
. Якщо 

 , то
, то  =
=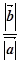
 , оскільки ці
вектори однаково напрямлені, то вони мають однакові модулі:
, оскільки ці
вектори однаково напрямлені, то вони мають однакові модулі: 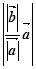 =
=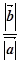
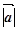 =
=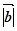 . Позначивши α =
. Позначивши α =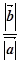 , дістанемо
, дістанемо  =α
=α . Якщо
. Якщо 
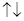
 , то аналогічно
доводиться, що
, то аналогічно
доводиться, що  = -
= -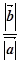
 . Нехай α =
-
. Нехай α =
-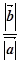 , тоді також
, тоді також  =
α
=
α .
.
2.
Достатність. Нехай виконується рівність /1/, тоді  і
і  або однаково, або протилежно напрямлені, а отже,
вони колінеарні. Теорему доведено.
або однаково, або протилежно напрямлені, а отже,
вони колінеарні. Теорему доведено.
Зауваження
1. Якщо  = 0,
= 0, 
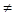 0, то теорема також справджується. У цьому
випадку α =0.
0, то теорема також справджується. У цьому
випадку α =0.
Зауваження
2. Оскільки для колінеарних векторів  і
і  завжди існує тільки одне число α таке, що
завжди існує тільки одне число α таке, що  = α
= α  , то звідси
формально можна написати: α =
, то звідси
формально можна написати: α =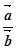 , тобто можна розглядати відношення
двох колінеарних векторів.
, тобто можна розглядати відношення
двох колінеарних векторів.
Відношення
 :
:  двох колінеарних
векторів розуміють як число, на яке треба помножити вектор
двох колінеарних
векторів розуміють як число, на яке треба помножити вектор  , щоб дістати вектор
, щоб дістати вектор  . Отже, відношенням
двох колінеарних векторів є число, яке дорівнює відношенню їх модулів, взяте зі
знаком «плюс», якщо
. Отже, відношенням
двох колінеарних векторів є число, яке дорівнює відношенню їх модулів, взяте зі
знаком «плюс», якщо
