Метод векторів та його застосування
розмірності. Введемо означення цих понять.Означення: базисом векторного простору називається система векторів, яка задана в певному порядку і задовольняє умови:
1) ця система векторів лінійно незалежна;
2) будь-який інший вектор із даного векторного простору є лінійною комбінацією даної системи векторів.
Інакше кажучи, базисом векторного простору називається максимальна система лінійно незалежних векторів даного векторного простору.
Означення: розмірністю векторного простору називається число векторів базису, тобто максимальна кількість лінійно незалежних векторів.
З попередніх теорем випливає, що базисом побудованого нами векторного простору є будь-яка система трьох не компланарних векторів, взятих у певному порядку. Справді, система будь-яких трьох некомланарних векторів лінійно незалежна, а за теоремою про розклад вектора за трьома не компланарними векторами будь-який вектор із даного векторного простору є лінійною комбінацією даної системи векторів.
Тому розмірність
даного простору 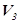 дорівнює трьом. У зв’язку з цим побудований
нами векторний простір називається тривимірним векторним простором.
дорівнює трьом. У зв’язку з цим побудований
нами векторний простір називається тривимірним векторним простором.
Означення:
нехай
L – непорожня
множина векторів із векторного простору 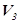 . Множина L називається
векторним підпростором простору
. Множина L називається
векторним підпростором простору 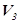 , якщо виконуються такі
умови:
, якщо виконуються такі
умови:
1)
якщо 
 L,
L, 
 L, то
L, то  +
+ 
 L;
L;
2)
якщо 
 L, то і α
L, то і α
 L
L 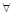 α
α  R.
R.
Тобто
підмножина L простору  буде векторним
підпростором простору
буде векторним
підпростором простору  , якщо вона сама є
векторним простором.
, якщо вона сама є
векторним простором.
6. Скалярний добуток векторів
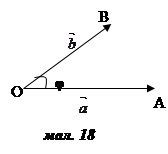
Нехай
 ,
,  − ненульові
вектори. Відкладемо від деякої точки O вектори
− ненульові
вектори. Відкладемо від деякої точки O вектори  =
= ,
, 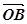 =
= . Кутом між векторами
. Кутом між векторами  і
і  називається кут між
променями OA і OB (мал. 18).
Позначають: (
називається кут між
променями OA і OB (мал. 18).
Позначають: ( ,
, ) = φ. Для будь-яких
векторів
) = φ. Для будь-яких
векторів  і
і  маємо 0 ≤ (
маємо 0 ≤ ( ,
, ) ≤ π.
) ≤ π.
Означення:
скалярним добутком двох векторів називається число, яке дорівнює
добутку їх довжин на косинус кута між ними: 
 =
=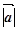
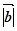 cos(
cos( ,
, ).
).
Теорема:
скалярний
добуток векторів  (
( ,
, 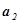 ,
, 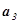 ),
),  (
(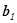 ,
, 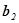 ,
, 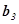 ), заданих в
ортонормованому базисі, обчислюються за формулою:
), заданих в
ортонормованому базисі, обчислюються за формулою:

 =
= 
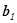 +
+ 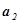
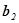 +
+
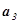
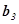 . /6/
. /6/
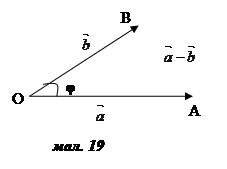
Доведення. Якщо один із
векторів або обидва нульові, то формула очевидна. Припустимо, що 
 ,
, 
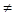
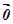 і розглянемо два випадки.
і розглянемо два випадки.
1.
Вектори  і
і  не колінеарні.
Відкладемо вектори
не колінеарні.
Відкладемо вектори 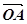 =
=  ,
, 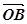 =
=  (мал. 19). Нехай (
(мал. 19). Нехай ( ,
,  ) = φ.
) = φ.
З  OAB за теоремою
косинусів
OAB за теоремою
косинусів 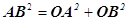 – 2 OAOBcosφ, або
– 2 OAOBcosφ, або 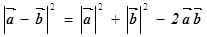 ,
,
звідки

=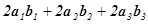 . Отже,
. Отже, 
 =
=

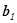 +
+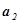
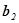 +
+ 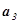
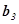 .
.
2.
Вектори  і
і  колінеарні. Тоді
колінеарні. Тоді  = λ
= λ ,
,  =
λ
=
λ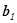 ,
, 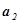 = λ
= λ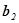 ,
, 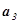 = λ
= λ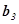 ;
;

 = λ
= λ
 =
= 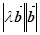 cos(λ
cos(λ ,
,  ) = λ
) = λ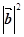 = λ(
= λ(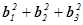 ) = λ
) = λ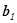
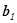 + λ
+ λ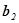
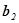 + λ
+ λ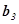
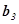 =
= 
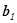 +
+ 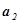
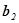 +
+
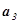
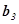
Теорему доведено.
З теореми і означення випливають такі властивості скалярного добутку векторів:
1. 
 = 0 тоді і тільки тоді, коли
= 0 тоді і тільки тоді, коли 
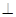
 , якщо
, якщо 
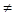
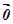 ,
, 
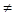
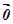 .
.
2. 
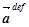 =
= 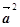 =
=

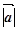 =
= 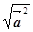 .
.
3. 
 =
= 
 .
.
4.
(α  )
)  = α(
= α(
 ),
),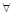 α
α  R;
R;
5. ( +
+  )
)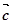 =
= 
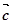 +
+ 
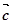 .
.
Формула,
аналогічна до формули /6/, має місце і в просторі 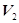 . Справді, нехай в
ортонормованому базисі простору
. Справді, нехай в
ортонормованому базисі простору 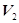 задано вектори
задано вектори  (
( ,
, 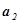 ),
),  (
(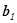 ,
, 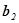 ). Тоді, користуючись
властивостями 1–5, дістанемо:
). Тоді, користуючись
властивостями 1–5, дістанемо: 
 = (
= (
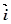 +
+ 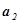
 )(
)(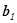
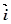 +
+
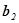
 )=
)= 
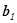
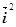 + (
+ (
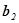 +
+ 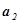
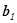 )
)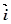
 +
+ 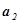
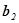
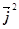 =
= 
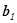 +
+ 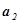
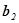 . Отже,
. Отже, 
 =
= 
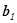 +
+
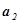
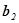 /7/
/7/
З означення скалярного добутку і /6/, /7/ випливають такі формули для обчислення косинуса кута між векторами:
– у
просторі 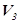 :
:
cos( ,
,  ) =
) = 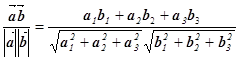 ;
;
– в просторі 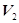 :
:
cos( ,
,  ) =
) = 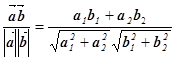 .
.
Векторна алгебра може ефективно використовуватися для розв’язування задач елементарної геометрії.
Практична частина
Задача
1.
Довести, що коли точка D ділить відрізок AB у відношеннях m: n, а C – довільна точка
площини, то 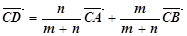 /*/.
/*/.
Доведення: Введемо позначення:
AD: DB = m: n; 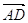 =
=  ;
; 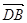 =
= 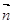 .
.
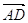 ||
|| 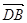

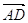 =
= 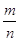
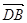 , але
, але 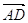 =
= 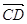 –
–  ,
,
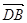 =
= 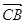 –
– 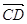 , тому
, тому 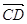 –
–  =
= 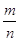
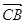 –
– 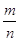
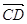 .
.
Звідси
(1 + 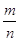 )
)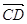 =
=  +
+ 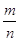
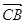 , і остаточно
, і остаточно 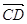 =
= 
 +
+ 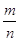
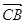 , що і треба було
довести.
, що і треба було
довести.
Задача
2.
Якщо точки M і N належать відрізкам AB і CD, та AM: MB = CN: ND = m: n, то виконується
рівність 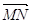 =
= 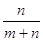
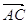 +
+

 .
.
Доведення:
за умовою та за формулою, що була доведена в задачі 1, маємо: 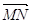 =
=
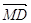 +
+
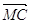 =
= (
(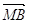 +
+ )+
)+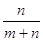 (
(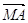 +
+ )=
)=
 +
+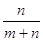
 +
+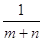 (m
(m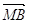 +
+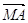 n). Вираз m
n). Вираз m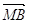 +n
+n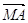 =
= 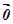 , отже ми довели,
що і треба було довести.
, отже ми довели,
що і треба було довести.
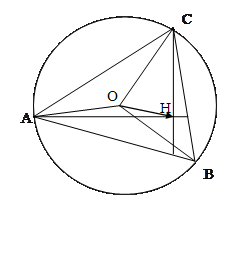 Задача 3. У трикутнику ABC точка O – центр
описаного кола, H – точка перетину його висот. Довести, що
Задача 3. У трикутнику ABC точка O – центр
описаного кола, H – точка перетину його висот. Довести, що 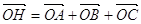 .
.
Доведення: за умовою 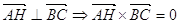 (за означенням скалярного добутку). Проте,
(за означенням скалярного добутку). Проте, 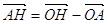 ,
, 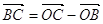 , тому (
, тому (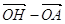 )(
)(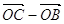 )=0 /1/. Крім того,
)=0 /1/. Крім того, 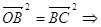 (
(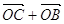 )(
)(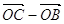 )=0 /2/ (як радіуси
описаного кола). Віднімаючи /2/ від /1/, матимемо (
)=0 /2/ (як радіуси
описаного кола). Віднімаючи /2/ від /1/, матимемо (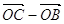 )(
)(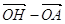 –
– 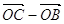 ) = 0. Аналогічно з умов
) = 0. Аналогічно з умов 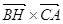 = 0 і
= 0 і 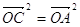 , маємо (
, маємо (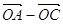 )(
)(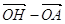 –
– 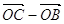 )
= 0. Оскільки
)
= 0. Оскільки 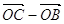
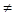
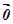 і
і 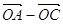
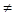
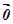 , то вектор,
перпендикулярний до кожного з них, може бути тільки нульовим, тобто
, то вектор,
перпендикулярний до кожного з них, може бути тільки нульовим, тобто 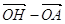 –
– 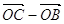 = 0. Звідси
= 0. Звідси 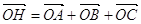 , що і треба було довести.
, що і треба було довести.
Задача 4. В коло вписано чотирикутник ABCD, перетинаються в точці M. Через середину S сторони CD проведено пряму SM так, що
