Метод векторів та його застосування
(AB) (SM) = K. Довести, що AK: KB =
(SM) = K. Довести, що AK: KB = 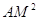 :
: 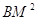 .
.
Доведення: позначимо AK: KB = x. Тоді за
формулою /*/ (див. задачу 1) 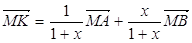 . Оскільки вектори
. Оскільки вектори 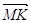 і
і
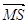 колінеарні, а точка S є серединою відрізка CD, то
колінеарні, а точка S є серединою відрізка CD, то 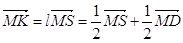 . Використавши рівність MA
. Використавши рівність MA 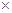 MC = MB
MC = MB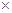 MD = k дістанемо
MD = k дістанемо  . Отже,
. Отже, 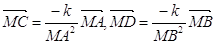 , а
, а
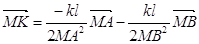 . За теоремою про єдність розкладу вектора за
двома не колінеарними векторами маємо
. За теоремою про єдність розкладу вектора за
двома не колінеарними векторами маємо

Звідси
x = 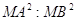 .
.
Задача
5.
Дано три точки A, B, C і деяка точка O. Довести, що рівність  /#/
при A
/#/
при A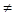 B є необхідною і достатньою умовою
належності точок A, B, C одній прямій.
B є необхідною і достатньою умовою
належності точок A, B, C одній прямій.
Доведення: Необхідність.
Нехай точки A, B, C належать одній прямій, тоді 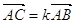 . Ця
рівність рівносильна такій
. Ця
рівність рівносильна такій 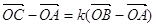 .Звідси
.Звідси  .
.
Достатність. Нехай  . Тоді
. Тоді 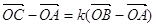 або
або 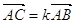 , тому
, тому  і
і 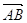 колінеарні, і, отже, A, B, C належать одній
прямій.
колінеарні, і, отже, A, B, C належать одній
прямій.
 Задача 6. Точка D належить стороні BC трикутника ABC. Довести, що
Задача 6. Точка D належить стороні BC трикутника ABC. Довести, що 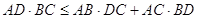 .
.
Доведення: за формулою /#/ маємо 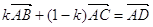 . Оскільки
. Оскільки 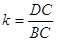
 . Отже,
. Отже,  , що і
треба було довести.
, що і
треба було довести.
Задача
7.
Довести, що косинус кута між медіанами катетів рівнобедреного трикутника
дорівнює  .
.
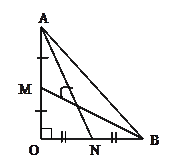 Доведення: нехай задано
рівнобедрений прямокутний трикутник OAB (OA = OB = a), точки M і N – відповідно
середини OA і OB. Розмістимо цей трикутник в прямокутну систему координат
так, щоб точка O збігалася з початком координат, а катети OA і OB лежали на
відповідних осях координат x і y. Тоді в цій системі координат матимемо A (a; 0), B (0; a), M(
Доведення: нехай задано
рівнобедрений прямокутний трикутник OAB (OA = OB = a), точки M і N – відповідно
середини OA і OB. Розмістимо цей трикутник в прямокутну систему координат
так, щоб точка O збігалася з початком координат, а катети OA і OB лежали на
відповідних осях координат x і y. Тоді в цій системі координат матимемо A (a; 0), B (0; a), M(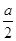 ; 0), N (0;
; 0), N (0;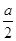 ). Вектори, які збігаються з медіанами,
матимуть координати
). Вектори, які збігаються з медіанами,
матимуть координати 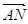 (-a;
(-a; 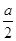 ) і
) і 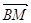 (
(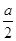 ;
a). Кут між
медіанами – це кут між векторами
;
a). Кут між
медіанами – це кут між векторами 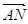 і
і 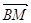 ,
який знайдемо за формулою: cos(
,
який знайдемо за формулою: cos(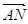 ,
,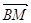 )
)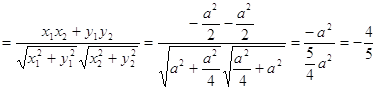 , що й треба було
довести.
, що й треба було
довести.
Задача 8. Довести, що медіани трикутника перетинаються в одній точці і діляться нею у відношенні 2: 1, рухаючи від вершин.
Доведення: нехай 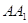 ,
, 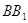 ,
, 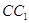 –
медіани трикутника ABC;
–
медіани трикутника ABC; 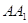 і
і 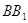 перетинаються
в точці O. Тоді
перетинаються
в точці O. Тоді 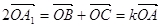 (бo
(бo 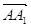 ||
|| 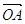 ) і
) і 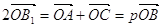 (бо
(бо 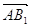 ||
||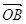 ). Звідси
). Звідси 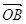 -
-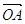 =
= 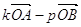 . Враховуючи єдність розкладу вектора за
двома неколінеарними векторами
. Враховуючи єдність розкладу вектора за
двома неколінеарними векторами 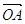 і
і 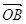 , знаходимо, що k = -1, – p = 1. Отже,
, знаходимо, що k = -1, – p = 1. Отже,  , то
, то  . За умовою
. За умовою 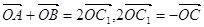 , тому
, тому 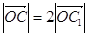 , або OC:
, або OC: 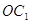 = 2: 1 і, отже, точки C, O,
= 2: 1 і, отже, точки C, O, 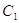 належать одній
прямій. З цього випливає, що медіана
належать одній
прямій. З цього випливає, що медіана 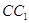 також проходить через
точку О і ділиться нею у відношенні 2: 1, рахуючи від вершини, що й треба було
довести.
також проходить через
точку О і ділиться нею у відношенні 2: 1, рахуючи від вершини, що й треба було
довести.
Задача
9. Дано правильну чотирикутну піраміду SABCD. Чи є лінійно
залежними вектори: а) 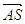 і
і  ; б)
; б) 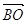 і
і 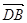 ; в)
; в) 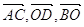 ; г)
; г) 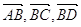 ; д)
; д) 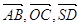 ; е)
; е)  ?
?
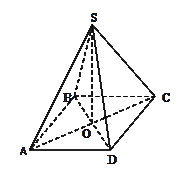 Розв’язання: вектори
Розв’язання: вектори 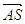 і
і  неколінеарні, тому за
теоремою про колінеарні вектори вони не є лінійно залежними.
неколінеарні, тому за
теоремою про колінеарні вектори вони не є лінійно залежними.
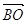 і
і 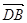 колінеарні, а тому
лінійно залежні.
колінеарні, а тому
лінійно залежні.
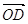 і
і 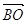 колінеарні, отже, лінійно
залежні; за властивістю три вектори
колінеарні, отже, лінійно
залежні; за властивістю три вектори 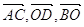 також лінійно залежні.
також лінійно залежні.
Вектори
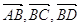 компланарні, тому за теоремою вони лінійно
залежні.
компланарні, тому за теоремою вони лінійно
залежні.
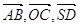 не є компланарними, за теоремою вони не є
лінійно залежними.
не є компланарними, за теоремою вони не є
лінійно залежними.
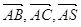 – три некомпланарні вектори. За теоремою про
розклад вектора за трьома не компланарними векторами, вектор
– три некомпланарні вектори. За теоремою про
розклад вектора за трьома не компланарними векторами, вектор 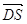 є лінійною комбінацією цих векторів. За
властивістю
є лінійною комбінацією цих векторів. За
властивістю  лінійно залежні.
лінійно залежні.
Задача
10. Обчислити кут між векторами 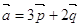 і
і 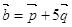 , де
, де  і
і 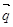 – одиничні взаємно перпендикулярні вектори.
– одиничні взаємно перпендикулярні вектори.
Розв’язання: формула косинуса
кута: cos( ,
,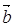 )=
)=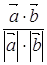 . Обчислимо
. Обчислимо 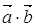 ,
, ,
,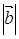 .
.
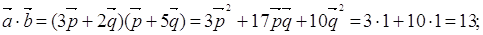
 ;
;
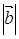
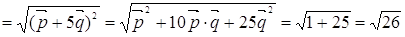 .
.
Тоді cos( ,
,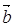 ) =
) = 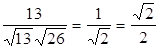 ; cos(
; cos( ,
,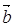 ) =
) = 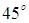 .
.
Відповідь:
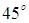 .
.
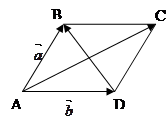 Задача 11. Довести, що сума
квадратів діагоналей паралелограма дорівнює сумі квадратів всіх його сторін.
Задача 11. Довести, що сума
квадратів діагоналей паралелограма дорівнює сумі квадратів всіх його сторін.
Розв’язання: Нехай ABCD – даний паралелограм.
Покладемо  ,
, 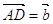 (
(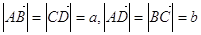 ).
За означенням суми і різниці векторів
).
За означенням суми і різниці векторів  .
Використовуючи властивості скалярного квадрату, отримаємо:
.
Використовуючи властивості скалярного квадрату, отримаємо: 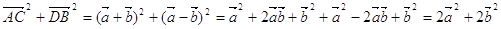 тобто
тобто  .
.
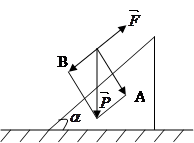 Задача 12. З якою силою F треба утримувати
вантаж вагою P на похилій площині, щоб він не скочувався вниз?
Задача 12. З якою силою F треба утримувати
вантаж вагою P на похилій площині, щоб він не скочувався вниз?
Розв’язання: нехай O – центр маси
вантажу, до якого прикладено силу P. Розкладемо вектор 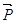 за двома взаємно
перпендикулярними напрямами, як показано на малюнку. Сила
за двома взаємно
перпендикулярними напрямами, як показано на малюнку. Сила 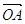 перпендикулярна до похилої площини і не викликає
переміщення вантажу. Сила F, яка утримує вантаж, має дорівнювати за
величиною і бути протилежною за напрямом силі OB. Тому F = P sinα.
перпендикулярна до похилої площини і не викликає
переміщення вантажу. Сила F, яка утримує вантаж, має дорівнювати за
величиною і бути протилежною за напрямом силі OB. Тому F = P sinα.
Висновок
Таким чином в своїй курсовій роботі на тему «Метод векторів та його застосування» я подала короткі теоретичні відомості про поняття вектора, рівносильність векторів, додавання, віднімання та множення вектора на число, колінеарність, компланарність, лінійну залежність векторів, координати вектора, скалярний добуток векторів а також про векторний простір та його підпростори. А в практичній частині, на прикладах показала доцільність його застосування. Метод векторів широко застосовується в різних галузях науки (математиці, фізиці). Часто його застосування значно полегшує розв’язування деяких задач, а інших випадках задачу взагалі неможливо розв’язати іншим способом.
Література
1. Базылев В.Т., Дуничев К.И., Иваницкая В.П. Геометрия, Ч.І. – М: Просвещение, 1974. – 351 с.
2. Атанасян Л.С., Базылев В.Т. Геометрия, Ч.І – М: Просвещение, 1986. – 336 с.
3. Атанасян Л.С. Геометрия, Ч.І – М: Просвещение, 1967. – 300 с.
4. Атанасян Л.С., Атанасян В.А. Сборник задач по геометри, Ч.І. – М: Просвещение, 1973. – 256 с.
5. Яковець, Боровик, Коваленко. Аналітична геометрія: навч. пос. – Суми: Університецька книга, 2004. – 295 с.
6. Цубербиллер О.Н. Задачи и упражнения по аналитической геометрии, М: Наука, 1970. – 335 с.
7. Клетенник Д.В. Сборник задач по аналитической геометри, М: Наука, 1972. – 240 с.
8. Панішева О.В. Векторний метод: Інтегрований урок геометрії та фізики, Математика. – 2000. – №14. – с. 4 – 5.
9. Єгорова Г.О. Векторний і координатний методи розв’язування задач, Математика. – 2001. – №5. – с. 5 – 11.
