Способы решения систем линейных уравнений

= 5; А₃₂ = 1 3 = –10;

–1 1 –3 1

А₃₃ = 1 2 = 5.

–3 –1

Составим присоединённую матрицу для матрицы А:

0 5 5

–1 –7 –10 .

–1 3 5

Отсюда находим обратную матрицу:

0 5 5

А^-1 = – –1 –7 –10 .

–1 3 5

-14-

Пример 2. Найти неизвестную матрицу Х из уравнения АХ = В, если:

А = 2 3 ; В = 3 4 .

1 2 -1 1

Р е ш е н и е. Умножив обе части данного матричного уравнения слева на матрицу А^-1, получим:

А^-1АХ = А^-1В; Х = А^-1В.

Найдем А^-1: ∆_А = 1, А₁₁ = 2, А₁₂ = -1, А₂₁ = -3, А₂₂ = 1, следовательно,

А^-1 = 2 -3 .

-1 1

Найдем матрицу Х:

Х = А^-1В = 2 -3 3 4 = 9 5 .

-1 1 -1 1 -4 -3

-15-

1.4. Ранг матрицы.

Рассмотрим произвольную прямоугольную матрицу

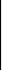
а₁₁ … а_1n

A = …………… (8)

a_m1 … a_mn

Выделим некоторое число k строк этой матрицы и такое же число столбцов. Элементы матрицы (8), стоящие на пересечение выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Если не все числа а_ij матрицы А равны нулю, то всегда можно указать число r такое, что у матрицы А имеется минор,

имеющий порядок r + 1 и выше, равен нулю.

Число r, представляющее собой наибольший из порядков отличных от нуля миноров матрицы А, называется рангом матрицы и обозначается rangA. Если все элементы а_ij равны нулю, то ранг матрицы принимается равным нулю. Отличный от нуля минор r-го порядка матрицы A (таких миноров у матрицы А может быть несколько, но все они имеют один и тот же порядок r) называется базисным минором матрицы А. Строки и столбцы, из которых построен базисный минор, называют базисными. Понятие ранга матрицы широко применяется в различных приложениях теории матриц.

Выделим в матрице А произвольно k строк. Пусть это будут строки

a₁, а₂, …, а_k:

а_α11, а_α12, …, а_α1n;

а_α21, а_α22, …, а_α2n;

……………………

а_αk1, а_αk2, …, а_αkn.

-16-

Если существуют такие числа λ₁, λ₂, …, λ_k, не все равные нулю, что для элементов некоторой другой, отличной от выделенной, строки i выполняются следующие соотношения:

(9)

то говорят, что i-я строка линейно выражается через строки

α₁, α₂, …, α_k. В случае, если равенства (9) выполняются тогда и только тогда, когда все числа λ₁, λ₂, …, λ_k – нули, то говорят, что i-я строка линейно зависима от строк α₁, α₂, …, α_k. Аналогичным образом можно ввести понятие линейной зависимости и линейной независимости между столбцами матрицы.

Теорема 1.2.(о базисном миноре) Любая строка матрицы А является линейной комбинацией её базисных строк.

Д о к а з а т е л ь с т в о. Предположим, что базисный минор матрицы (8) расположен в её верхнем левом углу, т.е. в первых r строках и первых r столбцах. Такое предположение не уменьшает общности рассуждения. Пусть k – номер любой строки матрицы А (k может принимать значения от 1 до m), а l – номер любого её столбца (l может принимать значения от 1 до n).

Рассмотрим следующий минор матрицы (8):

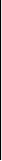
a₁₁ a₁₂ … a_1r a_1l

a₂₁ a₂₂ … a₁₁ a_1l

∆ = ……………………… (10)

a_r1 a_r2 … a_rr a_rl

………………………

a_k1 a_k2 … a_kr a_kl

Если k < r, то ∆ = 0, так как в нем имеется две одинаковые строки. Аналогично ∆ = 0 и при l < r.

Разложив определитель ∆ по элементам последнего столбца, получим

a_1lA_1l + a_2lA_2l + … + a_rlA_rl + a_klA_kl = 0,

-17-

Придавая l значения, получаем: