Цифровая схемотехника

прямой и инверсный выходы.

Мы рассмотрели практически все широко используемые при построении цифровых устройств логические элементы. Анализируя изложенный материал, можно придти к следующим выводам:

Существует возможность однозначного перехода от аналитического описания ЛЭ к его условному графическому обозначению либо к функциональной эквивалентной его схеме.

Существует возможность однозначного перехода от УГО элемента либо от его функциональной схемы к аналитическому его описанию. При этом функционирование элемента описывается алгебраическими выражениями логических функций, реализуемых элементом.

3. Функциональные схемы сложных ЛЭ можно построить на различных более простых (менее сложных) логических элементах, причём существует неоднозначность (многовариантность) построения функциональных эквивалентных схем для одного и того же ЛЭ.

Поскольку логические устройства по существу представляют собой совокупность взаимосвязанных логических элементов, то сформулированные выводы можно с успехом распространить и на устройства.

Вместе с тем возникает проблема, - каким образом можно построить устройствос минимальным количеством ЛЭ и на элементах минимальной номенклатуры. Другими словами, как построить устройство с минимальными аппаратурными затратами.

Решение этой проблемы основывается на знании функционально полных наборов логических элементов и выборе по определённым критериям соответствующего набора.

1.3.15. Функционально полные наборы логических элементов

Функционально полным называется такой набор ЛЭ, на которых (из которых) можно построить любое логическое устройство сколь сложно оно ни было бы. Функциональная полнота некоторого набора логических элементов, в свою очередь, определяется полнотой некоторой системы логических функций, которые являются логико-математическими моделями выбранного набора ЛЭ.

В булевой алгебре существует теорема Поста-Яблонского, согласно которой устанавливаются критерии полноты некоторой системы логических функций. Сущность этой теоремы сводится к следующему.

Некоторая система логических функций будет полной, если она содержит:

а) функцию, не сохраняющую логическую константу 0,

f (x1, x2, јxn) = f (0, 0, ј0) № 0;

б) функцию, не сохраняющую логическую константу 1,

f (x1, x2, јxn) = f (1, 1, ј1) № 1;

в) функцию, не являющуюся самодвойственной,

№ ;

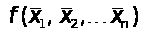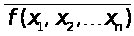г) функцию, не являющуюся линейной,

f (x1, x2, јxn) № х1 Е х2 Е јЕ хn Ех1 х2 Е ј Е х1 х2јxn;

д) функцию, не являющуюся монотонной.

Если Х1 есть некоторый фиксированный набор значений аргументов функции f (x1,x2,x3,x4), например Х1 = <x1, x2, x3, x4> = <1,1,0,1>, а Х2 = <x1, x2, x3, x4> = <0,0,0,1> - другой набор этих аргументов, то можно считать, что Х1 > Х2, т.е. набор Х2 меньше набора Х1.