Уравнение и функция Бесселя
/>) каждого ненулевого решения уравнения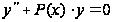 имеем
имеем
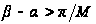 (это легко видеть,
если положить
(это легко видеть,
если положить
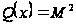 ,
взять
,
взять
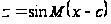 и заметить, что
нулями
и заметить, что
нулями
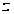 будут только
числа вида
будут только
числа вида
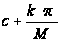 ,
,
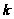 целое). Если
целое). Если
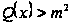 на
на
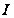 (где
(где
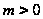 ),
то для всяких
двух соседних
нулей каждого
ненулевого
решения уравнения
),
то для всяких
двух соседних
нулей каждого
ненулевого
решения уравнения
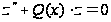 имеем
имеем
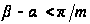 (это легко видеть,
если положить
(это легко видеть,
если положить
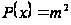 и взять
и взять
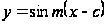 ).
Из сказанного
следует, что
если
).
Из сказанного
следует, что
если
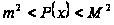 на
на
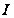 ,
то для всяких
двух соседних
нулей
,
то для всяких
двух соседних
нулей
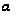 и
и
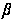 (
(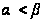 )
каждого ненулевого
решения уравнения
)
каждого ненулевого
решения уравнения
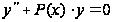 имеем
имеем
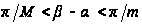 .
.
Изложенное
показывает,
что если
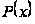 непрерывна
на
непрерывна
на
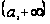 и превышает
некоторое
положительное
число вблизи
+∞, то каждое
ненулевое
решение
и превышает
некоторое
положительное
число вблизи
+∞, то каждое
ненулевое
решение
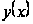 уравнения
уравнения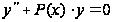 имеет на
имеет на
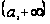 бесконечно
много нулей.
Если еще
бесконечно
много нулей.
Если еще
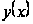 вблизи
вблизи
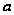 не обращается
в нуль, то эти
нули образуют
бесконечную
возрастающую
последовательность
не обращается
в нуль, то эти
нули образуют
бесконечную
возрастающую
последовательность
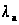 ,
имеющую пределом
+∞, а если, кроме
того,
,
имеющую пределом
+∞, а если, кроме
того,
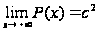 ,
где
,
где
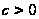 ,
то
,
то
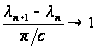 .
.
Рассмотрим уравнение Бесселя
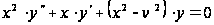
на интервале
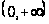 .
Подстановка
.
Подстановка
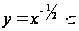 приводит к
уравнению
приводит к
уравнению
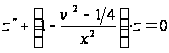 .
.
Очевидно,
 и
и
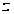 имеют одни и
те же нули. Так
как
имеют одни и
те же нули. Так
как
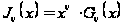 ,
где
,
где
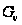 – целая функция,
то
– целая функция,
то
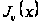 не имеет нулей
на
не имеет нулей
на
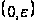 при достаточно
малом
при достаточно
малом
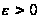 ,
и так как
,
и так как
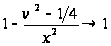 при
при
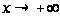 ,
то при каждом
,
то при каждом
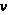 нули
нули
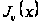 на
на
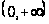 образуют бесконечную
возрастающую
последовательность
образуют бесконечную
возрастающую
последовательность
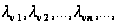
причем
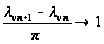 .
.
Если
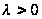 ,
то
,
то
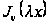 удовлетворит
уравнению
удовлетворит
уравнению
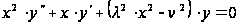
на интервале
(0, +∞). Подстановка
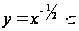 приводит к
уравнению
приводит к
уравнению
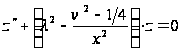
и, следовательно,
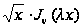 удовлетворяет
этому уравнению.
Таким образом,
при любых
положительных
удовлетворяет
этому уравнению.
Таким образом,
при любых
положительных
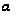 и
и
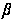 имеем
имеем
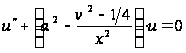 ,
где
,
где
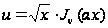 ,
,
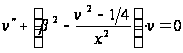 ,
где
,
где
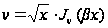 ,
,
откуда
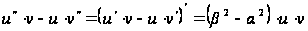 ,
,
следовательно,
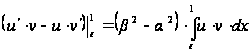 ,
где
,
где
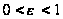 . (22)
. (22)
Пусть теперь
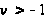 .
Разложение
.
Разложение
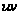 по степеням
по степеням
 начинается
с члена, содержащего
начинается
с члена, содержащего
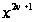 ,
разложение
,
разложение
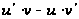 по степеням
по степеням
 начинается
с члена, содержащего
начинается
с члена, содержащего
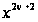 ,
так как коэффициент
при
,
так как коэффициент
при
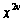 равен нулю, что
легко видеть,
исходя из формулы
(5). Следовательно,
из (22) при
равен нулю, что
легко видеть,
исходя из формулы
(5). Следовательно,
из (22) при
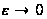 получим
получим
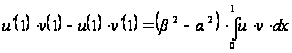 ,
,
то есть
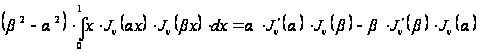 , (23)
, (23)
откуда видно,
что если
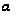 и
и
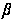 являются разными
нулями функции
являются разными
нулями функции
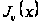 ,
то
,
то
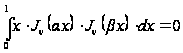 . (23`)
. (23`)
Этим доказано,
что при
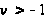 система функций
система функций
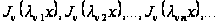
на интервале
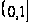 является
ортогональной
относительно
веса
является
ортогональной
относительно
веса
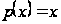 .
.
Переходя
к пределу при
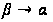 в соотношении
в соотношении
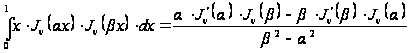
и используя
правило Лопиталя,
получим при
всяком
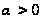
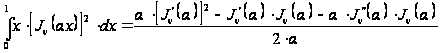 ,
(24)
,
(24)
следовательно,
если
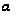 является нулем
функции
является нулем
функции
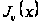 ,
то
,
то
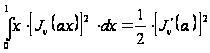 . (24`)
. (24`)
Таким образом,
при каждом
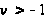 всякой непрерывной
функции
всякой непрерывной
функции
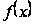 на
на
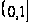 ,
удовлетворяющей
требованию
,
удовлетворяющей
требованию
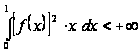 ,
,
поставлен в соответствие ряд Фурье-Бесселя
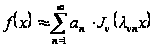 , (25)
, (25)
коэффициенты которого определяются формулами
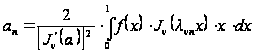 . (25`)
. (25`)
Можно доказать,
что система
функций
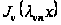 на
на
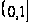 ,
ортогональная
относительно
веса
,
ортогональная
относительно
веса
 ,
замкнутая. В
частности, если
ряд Фурье-Бесселя
(25) равномерно
сходится к
порождающей
его непрерывной
функции
,
замкнутая. В
частности, если
ряд Фурье-Бесселя
(25) равномерно
сходится к
порождающей
его непрерывной
функции
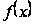 .
.
Можно показать,
что если
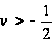 и
и
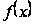 непрерывная
на
непрерывная
на
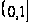 и кусочно-гладкая
на
и кусочно-гладкая
на
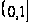 функция, то ряд
Фурье-Бесселя
этой функции
сходится к ней
при
функция, то ряд
Фурье-Бесселя
этой функции
сходится к ней
при
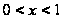 .
.
6. Асимптотическое представление бесселевых функций с целым индексом для больших значений аргумента
Пусть
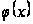 - положительная
функция и
- положительная
функция и
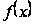 - какая-нибудь
(вообще комплекснозначная)
функция, определенные
для достаточно
больших значений
- какая-нибудь
(вообще комплекснозначная)
функция, определенные
для достаточно
больших значений
 .
Запись
.
Запись
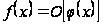 при
при
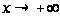
означает,
что найдутся
такие числа
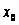 и M, что при
и M, что при
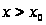 имеем
имеем
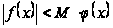 .
.
Подобная
запись употребляется
и в других
аналогичных
случаях. Например,
если
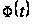 - положительная
функция и
- положительная
функция и
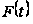 - какая-нибудь
функция, определенные
для достаточно
малых положительных
значений
- какая-нибудь
функция, определенные
для достаточно
малых положительных
значений
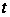 ,
то запись
,
то запись
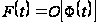 при
при
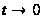
означает,
что найдутся
такие числа
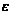 и
и
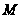 ,
что
,
что
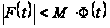 на
на
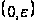 .
.
Вспомогательная лемма
Если
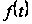 дважды непрерывно
дифференцируема
на
дважды непрерывно
дифференцируема
на
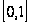 ,
то для функции
,
то для функции
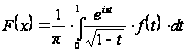
имеет место асимптотическое представление
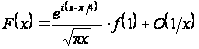 при
при
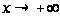 .
.
Докажем эту
лемму. Заменяя
на
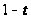 ,
получим:
,
получим:
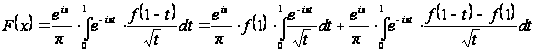 . (26)
. (26)
Рассмотрим
интеграл,
фигурирующий
в первом слагаемом
правой части
формулы (20). Заменяя
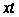 на
на
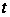 ,
найдем:
,
найдем:
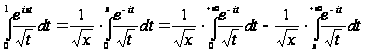 ,
,
но, заменив
на
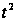 ,
получим:
,
получим:
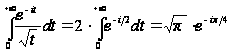 .
.
Если
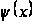 положительна,
убывает и стремиться
к нулю при
положительна,
убывает и стремиться
к нулю при
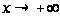 ,
то
,
то
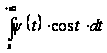 и
и
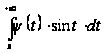 ,
а следовательно,
и
,
а следовательно,
и
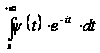 есть
есть
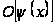 при
при
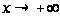 ,
поэтому
,
поэтому
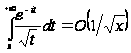 при
при
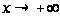 ,
,
откуда
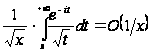 при
при
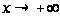 .
.
Итак, получаем асимптотическое представление:
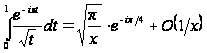 при
при
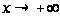 . (27)
. (27)
Рассмотрим теперь интеграл, фигурирующий во втором слагаемом правой части формулы (20). Имеем:
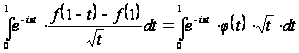 ,
,
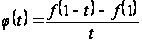 .
.
Очевидно,
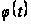 дважды непрерывно
дифференцируема
на
дважды непрерывно
дифференцируема
на
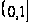 ,
но существуют
,
но существуют
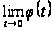 и
и
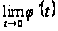 ,
поэтому
,
поэтому
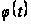 становится
непрерывно
дифференцируема
на
становится
непрерывно
дифференцируема
на
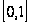 .
Интегрирование
по частям дает:
.
Интегрирование
по частям дает:
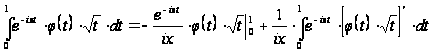 ,
,
где первое
слагаемое
правой части
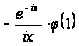 есть
есть
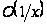 при
при
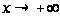 ,
а интеграл во
втором слагаемом
несобственный
при нижнем
пределе мажорируется
интегралом
,
а интеграл во
втором слагаемом
несобственный
при нижнем
пределе мажорируется
интегралом
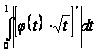 ,
,
который сходится, так как
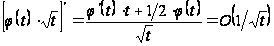 при
при
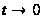 ;
;
следовательно,
второе слагаемое
есть тоже
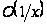 при
при
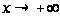 .
.
Итак, имеем:
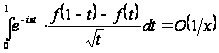 при
при
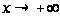 . (28)
. (28)
Из (26), (27),
