Методы интегрирования
alt="Методы интегрирования" width="53" height="26" align="BOTTOM" border="0" />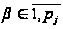 ).
После этого
равенства
приводятся
к общему знаменателю
и у получившихся
в числителе
многочленов
приравниваются
коэффициенты.
При этом, если
степень многочлена
).
После этого
равенства
приводятся
к общему знаменателю
и у получившихся
в числителе
многочленов
приравниваются
коэффициенты.
При этом, если
степень многочлена
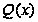 равна
равна
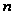 ,
то, вообще говоря,
в числителе
правой части
равенства (**)
после приведения
к общему знаменателю
получается
многочлен
степени
,
то, вообще говоря,
в числителе
правой части
равенства (**)
после приведения
к общему знаменателю
получается
многочлен
степени
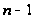 ,
т.е. многочлен
с
,
т.е. многочлен
с
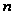 коэффициентами;
число же неизвестных
коэффициентами;
число же неизвестных
 так же равняется
так же равняется
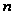 :
:
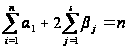 .
Таким образом,
мы получаем
систему
.
Таким образом,
мы получаем
систему
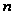 уравнений с
уравнений с
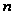 неизвестными.
неизвестными.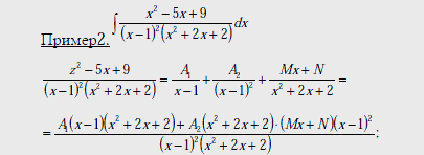
раскроем
скобки, располагаем
степени
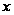 по убывающей,
получаем:
по убывающей,
получаем:
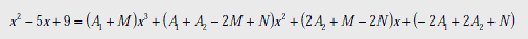
Сравниваем
коэффициенты
при одинаковых
степенях
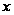 :
:

Решаем полученную систему, находим неизвестные коэффициенты:
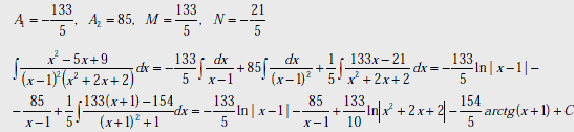
Варианты
Вычислить интегралы:
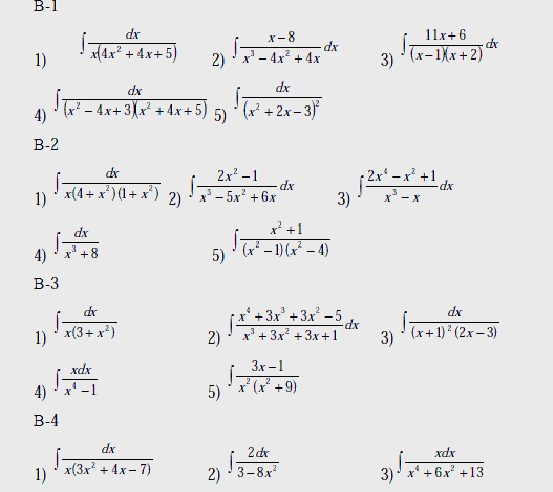
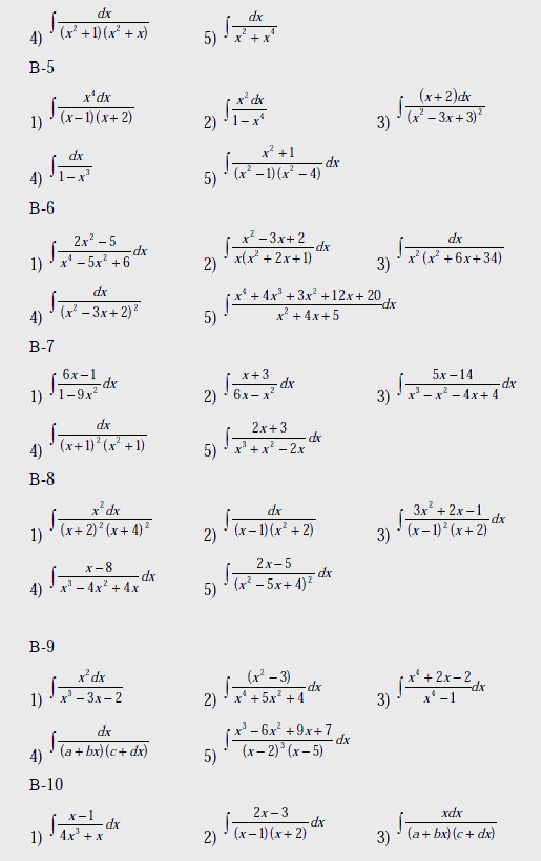
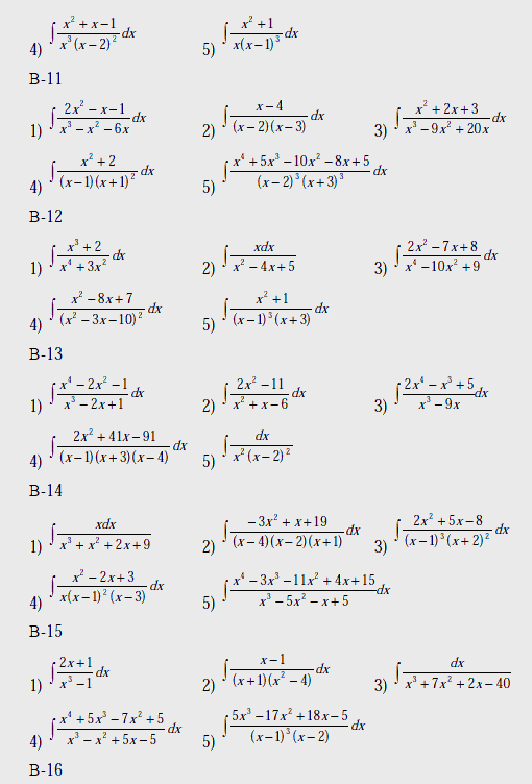

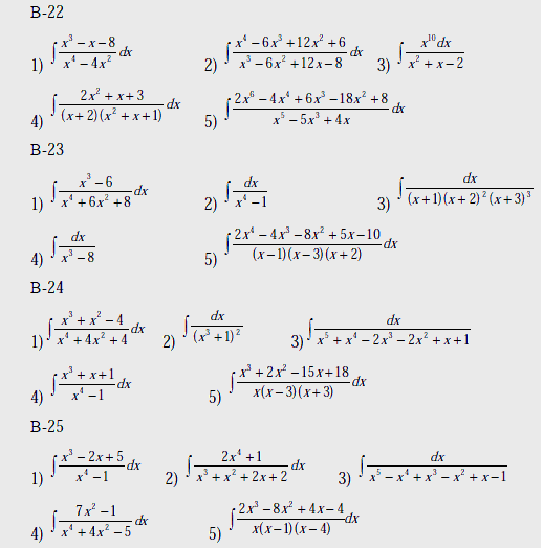
Вопросы к лабораторной работе №3
Приведите примеры интегралов, не выражающихся в конечном виде через элементарные функции.
В чем заключается характерная особенность класса рациональных функций?
Перечислить четыре типа простых дробей.
Покажите,
как вычисляется
интеграл вида
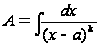
Покажите
подробно, как
вычисляется
интеграл вида
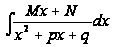 и какую при
этом выгодно
применить
подстановку.
и какую при
этом выгодно
применить
подстановку.
Покажите
подробно, как
вычисляется
интеграл вида
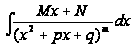 и какие подстановки
следует при
этом применять.
и какие подстановки
следует при
этом применять.
В чем состоит применение метода неопределенных коэффициентов к разложению правильной дроби в сумму простых?
8) С помощью каких функций выражается в конечном виде интеграл
от любой рациональной функции?
ЛАБОРАТОРНАЯ РАБОТА № 4
Интегрирование рациональных дробей. Метод Остроградского
Метод Остроградского позволяет чисто алгебраическим путем выделить рациональную часть интеграла.
Пусть имеем
правильную
дробь
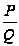 ,
которую будем
предполагать
несократимой,
и пусть знаменатель
ее Q
разложен на
простые множители
,
которую будем
предполагать
несократимой,
и пусть знаменатель
ее Q
разложен на
простые множители
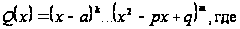
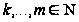 (*)
(*)
Тогда интеграл от этой дроби представится в виде суммы интегралов от дробей вида:
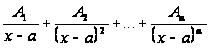 (1)
(1)
или
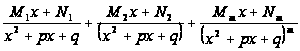 (2)
(2)
Если
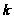 (или
(или
 )
больше единицы,
то интегралы
всех дробей
группы (1) или
(2) , кроме первой,
преобразуются
по формуле
)
больше единицы,
то интегралы
всех дробей
группы (1) или
(2) , кроме первой,
преобразуются
по формуле
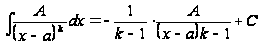
или
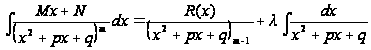
Объединяя все результаты, окончательно придем к формуле вида
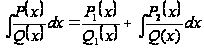 (3)
(3)
Рациональная
часть интеграла
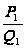 ,
получена от
сложения выделенных
выше рациональных
частей; следовательно,
прежде всего
она является
правильной
дробью, а ее
знаменатель
имеет разложение
,
получена от
сложения выделенных
выше рациональных
частей; следовательно,
прежде всего
она является
правильной
дробью, а ее
знаменатель
имеет разложение
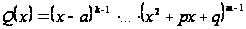
Что касается
дроби
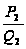 ,
оставшейся
под знаком
интеграла, то
она получилась
от сложение
дробей вида
I и
II
(Л. Р.№2), так что
она тоже правильная
и
,
оставшейся
под знаком
интеграла, то
она получилась
от сложение
дробей вида
I и
II
(Л. Р.№2), так что
она тоже правильная
и
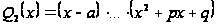 .
Очевидно , Q=
.
Очевидно , Q=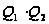 (см.(*)).
(см.(*)).
(3)называется
формулой
Остроградского.
Дифференцируя,
можно представить
ее в равносильной
форме

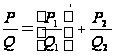 (4)
(4)
Так как
производная
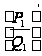 содержит
все простые
множители, на
которые разлагается,
то
содержит
все простые
множители, на
которые разлагается,
то
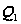 является наибольшим
общим делителем
является наибольшим
общим делителем
 и
и
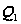 ,
так что
,
так что
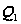 может быть
определено
по этим многочленам
(последовательным
делением). Тогда
может быть
определено
по этим многочленам
(последовательным
делением). Тогда
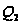 определяется
простым делением
определяется
простым делением
 на
на
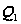 .
Обратимся к
определению
числителей
.
Обратимся к
определению
числителей
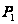 и
и
 в формуле (4).
в формуле (4).
Для этого используем метод неопределенных коэффициентов.
Перепишем (4) в виде:

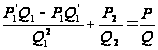 (5)
(5)
Покажем
теперь, что
первую дробь
всегда можно
привести к
знаменателю
 ,
сохранив целым
числитель.
Именно,
,
сохранив целым
числитель.
Именно,
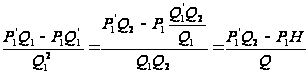 ,
(6)
,
(6)
где
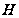 означает частное
означает частное
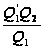 .
Освобождаясь
от общего знаменателя
.
Освобождаясь
от общего знаменателя
 ,
придем к тождеству
двух многочленов
(сравни (5) и (6)).
,
придем к тождеству
двух многочленов
(сравни (5) и (6)).
Пример.
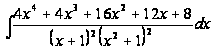
Имеем

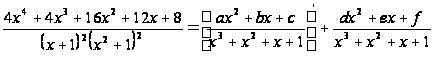 .
.
Откуда
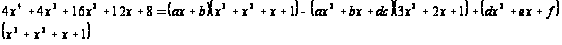
Приравнивая коэффициенты при одинаковых степенях в обеих частях , получим:
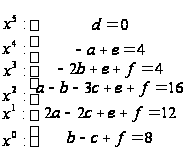
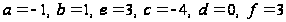
Таким образом,
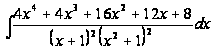 =-
=-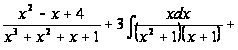

Варианты
Вычислить интегралы:
В-1
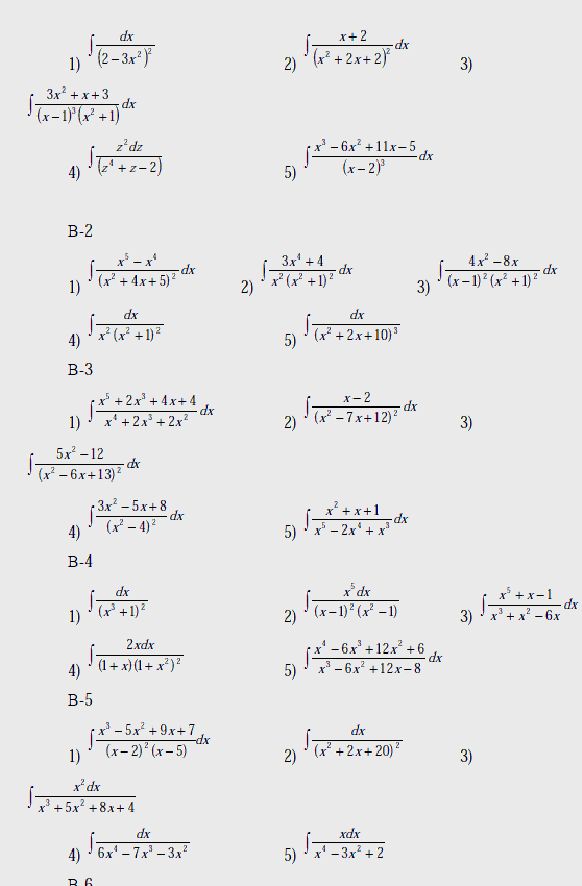
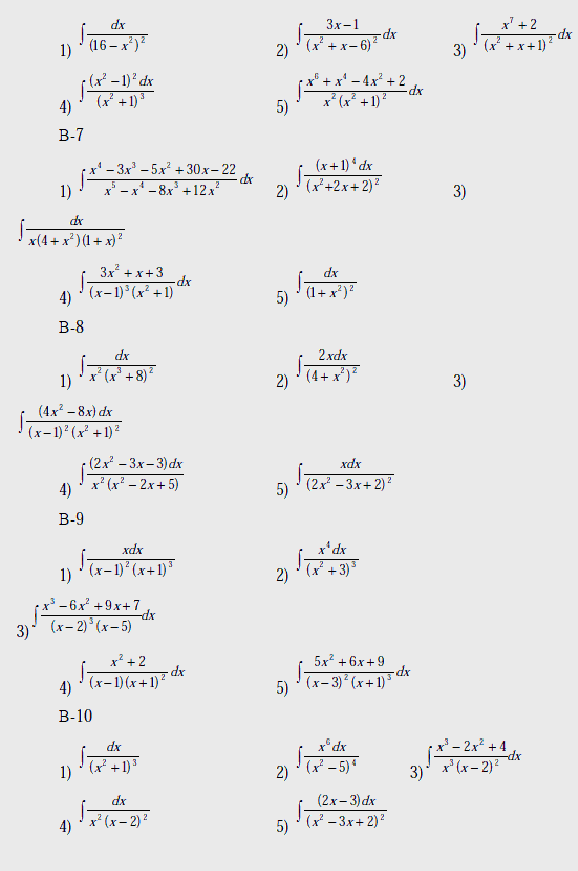
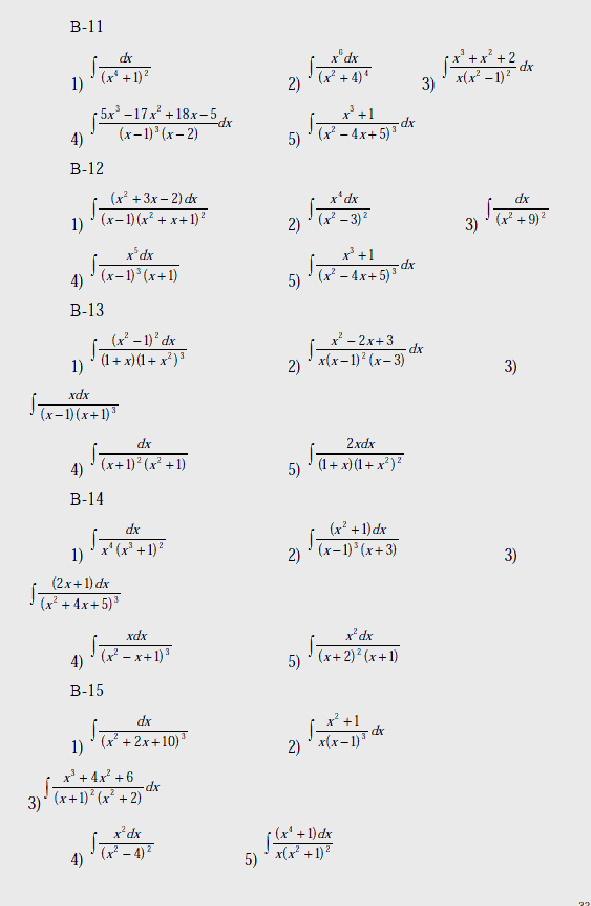
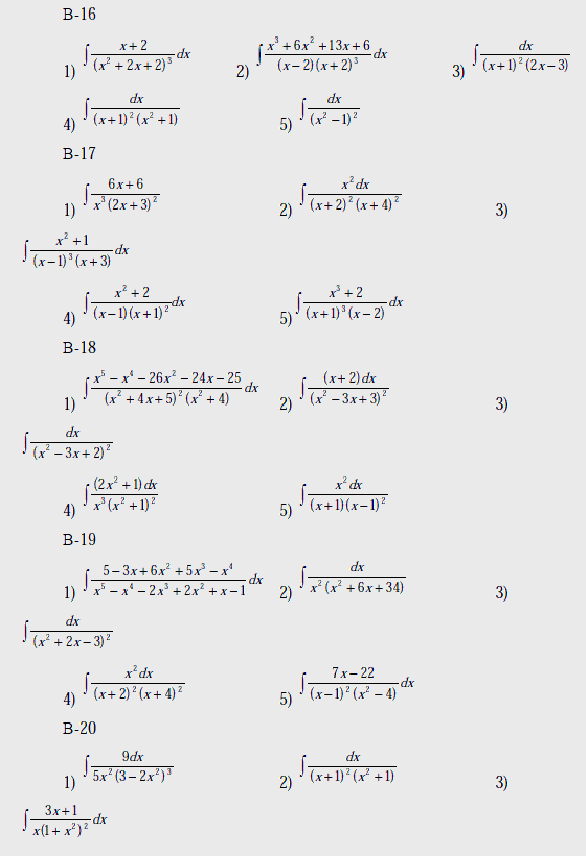

Вопрос к лабораторной работе №4
1. В чем заключается метод Остроградского и когда им пользуются?
ЛАБОРАТОРНАЯ РАБОТА №5
Интегрирование тригонометрических функций
Дифференциалы вида
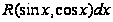 ,
(I)
,
(I)
где
 -
рациональная
функция от двух
переменных,
могут быть
приведены к
более простому
виду с помощью
подстановки
-
рациональная
функция от двух
переменных,
могут быть
приведены к
более простому
виду с помощью
подстановки
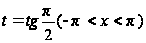 . (*)
. (*)
При этом используется формулы из тригонометрии:
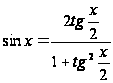 ;
;
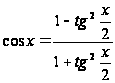 ;
;
Тогда:
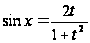 ;
;
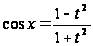 ;
;
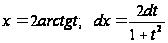 (**)
(**)
Подстановка (*) называется универсальной тригонометрической подстановкой.
Пример1.
Вычислить
интеграл
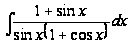
Решение:
Сделаем подстановку
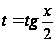 ,
пользуясь (**),
получим
,
пользуясь (**),
получим
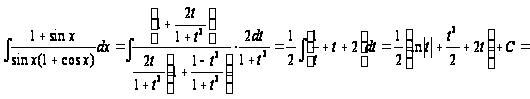
=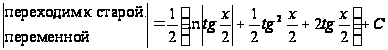
В некоторых случаях можно использовать более простые подстановки. Рассмотрим эти случаи.
Замечание
1: Если целая
или дробная
рациональная
функция
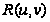 не меняет своего
значения при
изменении знака
у одного из
аргументов,
например, т. е.
не меняет своего
значения при
изменении знака
у одного из
аргументов,
например, т. е.
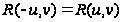 ,
то она может
быть приведена
к виду
,
то она может
быть приведена
к виду
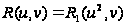 ,
содержащему
лишь четные
степени
,
содержащему
лишь четные
степени
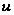 .
.
Если же, наоборот,
при изменении
знака
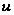 функция
функция
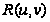 так же меняет
знак, т.е.
так же меняет
знак, т.е.
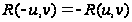 ,
то она проводится
к виду
,
то она проводится
к виду
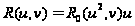 .
.
Рассмотрим три случая:
1. Пусть теперь
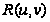 меняет знак
при изменении
знака
меняет знак
при изменении
знака
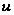 ,
тогда
,
тогда
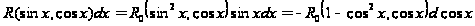
и рационализация
достигается
подстановкой
 .
.
2. Аналогично,
если
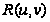 меняет знак
при изменении
знака
меняет знак
при изменении
знака
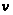 ,
то
,
то
 ,
,
так что здесь
целесообразна
подстановка
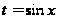 .
.
3. Предположим,
наконец, что
функция
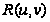 не меняет своего
значения при
одновременном
изменении
знаков
не меняет своего
значения при
одновременном
изменении
знаков
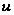 и
и
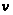 :
:
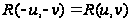 .
В этом случае,
заменяя
.
В этом случае,
заменяя
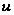 на
на
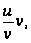 будем иметь:
будем иметь:
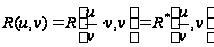 .
По свойству
функции R
, если изменить
знаки
.
По свойству
функции R
, если изменить
знаки
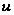 и
и
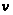 (отношение
(отношение
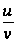 при этом изменяется):
при этом изменяется):
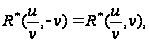 а тогда, как
мы знаем
а тогда, как
мы знаем
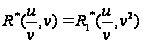 .
.
Поэтому
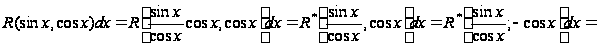
=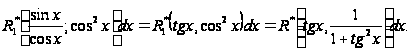
Поэтому здесь
используется
подстановка
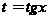 .
.
Замечание
2. Каково бы ни
было рациональное
выражение
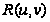 ,
его можно представить
в виде суммы
трех выражений
рассмотренных
типов:
,
его можно представить
в виде суммы
трех выражений
рассмотренных
типов:
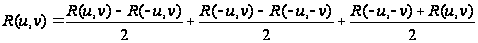
Первое из
этих выражений
меняет знак
при изменении
знака
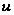 ,
второе меняет
знак при изменении
,
второе меняет
знак при изменении
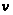 ,
а третье сохраняет
значение при
одновременном
изменении
знаков
,
а третье сохраняет
значение при
одновременном
изменении
знаков
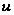 и
и
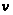 .
Разбив
.
Разбив
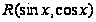 на соответствующие
слагаемые,
можно к первому
из них применить
подстановку
на соответствующие
слагаемые,
можно к первому
из них применить
подстановку
 ,
ко второму -
подстановку
,
ко второму -
подстановку
 и, наконец, к
третьему -
подстановку
и, наконец, к
третьему -
подстановку
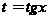 .
Таким образом,
для вычисления
.
Таким образом,
для вычисления
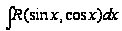 достаточно
этих трех
подстановок.
достаточно
этих трех
подстановок.
Пример
2. Вычислить
интеграл:
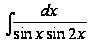
Решение:
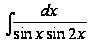 =
=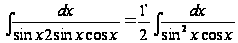
Если в
выражение
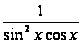 подставим
подставим
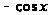 в место
в место
 ,
то дробь изменит
знак на противоположный,
поэтому здесь
выгодна подстановка
,
то дробь изменит
знак на противоположный,
поэтому здесь
выгодна подстановка
 .
.
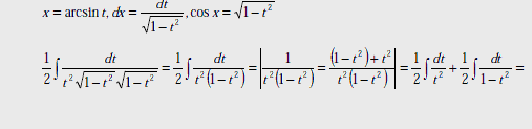
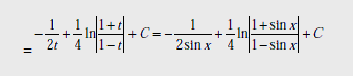
Пример
3. Вычислить
интеграл
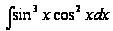
Решение:
в этом случае
можно сделать
замену
 .
.
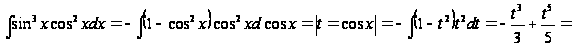
=
Интегралы
от квадратов
и других четных
степеней
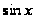 и
и
 находят, применяя
формулы понижение
степени:
находят, применяя
формулы понижение
степени:
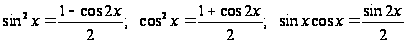 .
.
Задача. Интегрируя по частям, вывести формулы понижения степени:
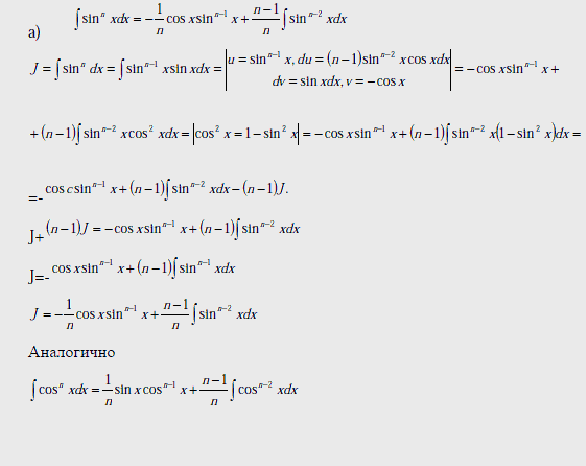
Варианты
Вычислить интегралы:
В-1




Вопросы к лабораторной работе №5
1) Назовите
универсальную
подстановку,
с помощью которой
всегда достигается
рационализация
дифференциала
вида (1)
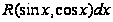 ,
и покажите, как
ею пользоваться.
,
и покажите, как
ею пользоваться.
2) В каких
условиях
рационализация
дифференциала
(1) достигается
подстановкой
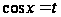 ?
Приведите
доказательство.
?
Приведите
доказательство.
3) В каких
случаях рационализация
дифференциала
(1) достигается
подстановкой
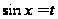 ?
Приведите
доказательство.
?
Приведите
доказательство.
4) В каких случаях рационализация дифференциала (1) достигается подстановкой
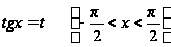 ?
?
5) Что такое «интегральный логарифм», «интегральный синус» и «интегральный косинус»?
6) Выведите
рекуррентные
формулы для
вычисления
интегралов
вида
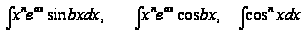 .
.
ЛАБОРАТОРНАЯ РАБОТА №6
Интегрирование некоторых выражений, содержащих радикалы
Интегрирование выражений вида
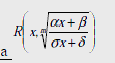
Рассмотрим интеграл вида
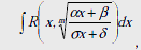 ,
(1)
,
(1)
где
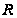 означает рациональную
функцию от двух
аргументов,
означает рациональную
функцию от двух
аргументов,
 -
натуральное
число,
-
натуральное
число,
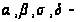 постоянные,
причем
постоянные,
причем
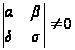 .
Полагаем
.
Полагаем
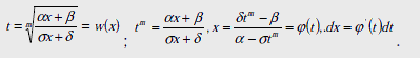 ;.
;.
Интеграл
(I)
примет вид:
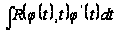 здесь дифференциал
имеет уже
рациональный
вид, так как
здесь дифференциал
имеет уже
рациональный
вид, так как
 - рациональные
функции.
- рациональные
функции.
Вычислив
этот интеграл
как интеграл
от рациональной
функции, вернемся
к старой переменной,
подставив
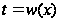 .
.
К интегралу вида (I) сводятся и более общие интегралы
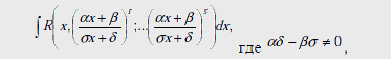
где все
показатели
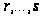 – рациональны;
стоит лишь
привести эти
показатели
к общему знаменателю
– рациональны;
стоит лишь
привести эти
показатели
к общему знаменателю
 ,
чтобы под знаком
интеграла
получить рациональную
функцию от
,
чтобы под знаком
интеграла
получить рациональную
функцию от
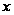 и от радикала
и от радикала
 .
.
Пример 1.
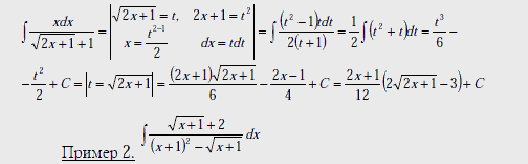
Здесь
дробно-линейная
функция
 сводится к
линейной функции:
сводится к
линейной функции:

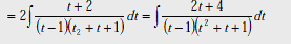
Разложим данную дробь на простейшие
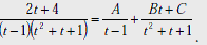
Приведем к общему знаменателю правую часть равенства и приравняем числители, получим:

Приравняв
коэффициенты
при одинаковых
степенях
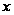 в правой и левой
частях, получим
систему уравнений:
в правой и левой
частях, получим
систему уравнений:
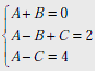 .
Решив систему,
получим
.
Решив систему,
получим
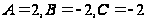 .
.
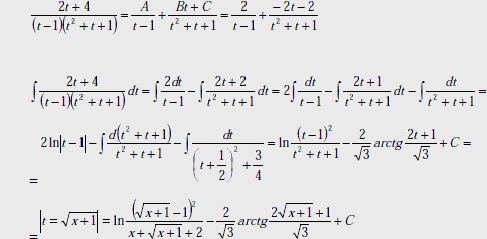
Интегрирование биноминальных дифференциалов
Биноминальными называются дифференциалы вида
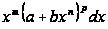 ,
(2)
,
(2)
где
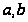 –любые постоянные,
а показатели
–любые постоянные,
а показатели
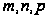 -
рациональные
числа.
-
рациональные
числа.
Если
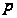 -
число целое,
то мы получим
выражение,
изученное в
I.
Именно, если
через
-
число целое,
то мы получим
выражение,
изученное в
I.
Именно, если
через
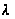 обозначить
наименьшее
общее кратное
знаменателей
обозначить
наименьшее
общее кратное
знаменателей
 ,
то будем иметь
выражение вида
,
то будем иметь
выражение вида
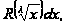 для рационализации
которого достаточна
подстановка
для рационализации
которого достаточна
подстановка
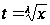 .
.
Пусть
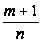 -
целое. Преобразуем
теперь данное
выражение
подстановкой
-
целое. Преобразуем
теперь данное
выражение
подстановкой
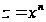 .
Тогда
.
Тогда
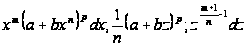 и положив для
краткости
и положив для
краткости
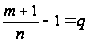 будем иметь
будем иметь
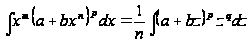 (3)
(3)
Если
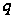 – целое число,
то снова приходим
к выражению
изученного
типа (2). Если
обозначить
через
– целое число,
то снова приходим
к выражению
изученного
типа (2). Если
обозначить
через
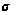 знаменатель
дроби
знаменатель
дроби