Оптимальність у системах керування
1. Умови оптимальності у неавтономних системах керування
У
загальному
випадку неавтономної
системи права
частина закону
руху й підінтегральна
функція цільового
функціонала
залежать явно
від часу
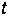 ,
тобто закон
руху має вигляд:
,
тобто закон
руху має вигляд:
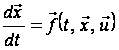 ,
(1)
,
(1)
а цільовий функціонал дорівнює
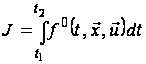 .
(2)
.
(2)
Тут
функції
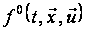 і
і
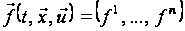 – неперервні
по сукупності
змінних і неперервно
диференційовані
по змінних
– неперервні
по сукупності
змінних і неперервно
диференційовані
по змінних
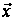 ,
,
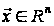 ,
,
 .
.
Також
вважатимемо,
що момент часу
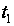 ,
який відповідає
початковому
стану
,
який відповідає
початковому
стану
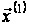 ,
відомий, а момент
часу
,
відомий, а момент
часу
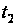 проходження
через кінцеву
точку
проходження
через кінцеву
точку
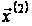 не заданий і
повинен бути
знайдений,
тобто сформульована
задача – це
задача з вільним
часом.
не заданий і
повинен бути
знайдений,
тобто сформульована
задача – це
задача з вільним
часом.
Поставлена
задача може
бути зведена
до автономної
задачі введенням
додаткової
змінної
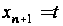 .
До закону руху
при цьому додається
рівняння
.
До закону руху
при цьому додається
рівняння
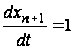 ,
,
а
до початкових
умов – співвідношення
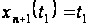 .
.
Тепер систему (2) можна переписати у вигляді:
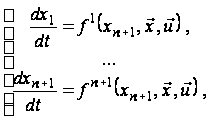 (3)
(3)
а
функціонал
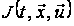 дорівнюватиме
дорівнюватиме
 ,
(4)
,
(4)
де
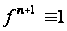 (відповідно
до доданого
у початкову
систему рівняння).
(відповідно
до доданого
у початкову
систему рівняння).
Отже,
неавтономну
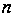 -вимірну
задачу було
зведено до
автономної
задачі з розширеним
фазовим простором.
У новій задачі
потрібно знайти
оптимальну
траєкторію,
що поєднує
точку
-вимірну
задачу було
зведено до
автономної
задачі з розширеним
фазовим простором.
У новій задачі
потрібно знайти
оптимальну
траєкторію,
що поєднує
точку
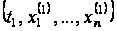 розширеного
фазового простору
з деякою точкою
розширеного
фазового простору
з деякою точкою
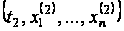 на прямій, яка
проходить через
точку
на прямій, яка
проходить через
точку
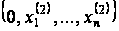 паралельно
осі
паралельно
осі
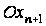 .
Оскільки кінцеве
значення
.
Оскільки кінцеве
значення
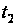 змінної
змінної
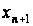 невідоме, то
нова задача
– це задача з
фіксованим
лівим і рухомим
правим кінцями.
невідоме, то
нова задача
– це задача з
фіксованим
лівим і рухомим
правим кінцями.
Якщо
в задачі оптимального
керування (3) –
(4) відомі і початковий
момент часу
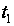 й кінцевий
момент часу
й кінцевий
момент часу
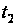 ,
то задача називається
задачею з фіксованим
часом. Перетворення
цієї задачі
введенням
додаткового
змінного приводить
до задачі з
фіксованими
кінцями в такому
формулюванні.
Потрібно знайти
керування
,
то задача називається
задачею з фіксованим
часом. Перетворення
цієї задачі
введенням
додаткового
змінного приводить
до задачі з
фіксованими
кінцями в такому
формулюванні.
Потрібно знайти
керування
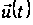 ,
що переводить
фазову точку
системи (2) зі
стану
,
що переводить
фазову точку
системи (2) зі
стану
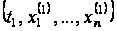 в момент часу
в момент часу
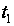 у стан
у стан
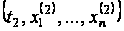 в момент часу
в момент часу
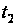 ,
причому функціонал
(4) набуває найменшого
значення. Зауважимо,
що момент часу
,
причому функціонал
(4) набуває найменшого
значення. Зауважимо,
що момент часу
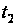 попадання в
точку
попадання в
точку
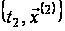 можна не вважати
фіксованим,
оскільки в силу
тотожності
можна не вважати
фіксованим,
оскільки в силу
тотожності
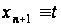 попадання в
точку
попадання в
точку
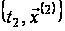 може відбутися
тільки в цей
момент часу.
Таким чином,
до даної задачі
можна застосувати
теорему, відповідно
до якої для
одержання
необхідних
умов екстремуму
функціонала
необхідно
максимізувати
функцію Понтрягіна
може відбутися
тільки в цей
момент часу.
Таким чином,
до даної задачі
можна застосувати
теорему, відповідно
до якої для
одержання
необхідних
умов екстремуму
функціонала
необхідно
максимізувати
функцію Понтрягіна
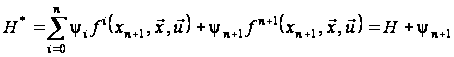 ,
(5)
,
(5)
де
 – загальний
вигляд функції
Понтрягіна
з теореми 1, у
якій не врахована
додаткова,
(
– загальний
вигляд функції
Понтрягіна
з теореми 1, у
якій не врахована
додаткова,
(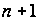 )-ша
змінна. Спряжена
система для
цієї задачі
за умов
)-ша
змінна. Спряжена
система для
цієї задачі
за умов
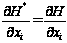 набуває вигляду:
набуває вигляду:
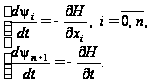 (6)
(6)
Має місце така теорема.
Припустимо,
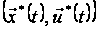 ,
,
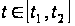 – оптимальний
процес для
задачі з фіксованим
часом. Тоді
існує ненульова
вектор-функція
– оптимальний
процес для
задачі з фіксованим
часом. Тоді
існує ненульова
вектор-функція
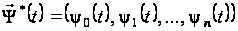 ,
що відповідає
цьому процесу,
така що:
,
що відповідає
цьому процесу,
така що:
1.
Для будь-якого
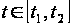 функція
функція
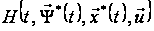 змінної
змінної
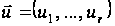 набуває максимального
значення в
точці
набуває максимального
значення в
точці
 ,
тобто:
,
тобто:
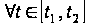 :
:
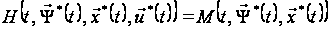 .
.
2.
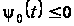 ,
,
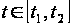 .
.
Оскільки,
як і раніше,
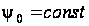 ,
то умову 2 цієї
теореми достатньо
перевірити
в якій-небудь
одній точці
відрізка
,
то умову 2 цієї
теореми достатньо
перевірити
в якій-небудь
одній точці
відрізка
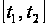 .
.
Розглянемо
випадок, коли
при фіксованому
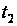 правий кінець
вільний. Ця
задача полягає
в тому, щоб із
заданого стану
правий кінець
вільний. Ця
задача полягає
в тому, щоб із
заданого стану
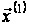 за заданий час
за заданий час
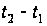 пройти по траєкторії
з довільним
кінцевим станом
за умови мінімізації
цільового
функціонала.
Умови трансверсальності
для цієї задачі
набувають
вигляду:
пройти по траєкторії
з довільним
кінцевим станом
за умови мінімізації
цільового
функціонала.
Умови трансверсальності
для цієї задачі
набувають
вигляду:
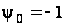 ,
,
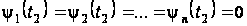 .
(7)
.
(7)
Для
цього випадку
необхідна умова
оптимальності
полягає в тому,
щоб функція
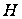 досягала
максимального
значення для
кожного
досягала
максимального
значення для
кожного
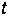 на оптимальному
керуванні
на оптимальному
керуванні
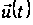 і мала місце
умова (7).
і мала місце
умова (7).
2 Поняття особливого керування
На
практиці часто
зустрічаються
задачі оптимального
керування, у
яких функція
Понтрягіна
лінійно залежить
від всіх керувань
або від частини
з них (наприклад,
в лінійних
задачах оптимальної
швидкодії).
Однак у нелінійних
задачах оптимального
керування (якщо
функція Понтрягіна
є нелінійною
по одній або
декількох
фазових змінних)
можлива ситуація,
коли на оптимальній
траєкторії
коефіцієнт
при одній з
компонент
вектора керування
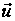 обертається
на нуль всюди
на деякому
інтервалі часу,
і тоді умова
максимуму
функції
обертається
на нуль всюди
на деякому
інтервалі часу,
і тоді умова
максимуму
функції
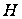 за
за
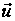 не дозволяє
однозначно
визначити
оптимальне
керування. Ця
ситуація називається
особливим
режимом керування.
Дослідимо її
детальніше.
не дозволяє
однозначно
визначити
оптимальне
керування. Ця
ситуація називається
особливим
режимом керування.
Дослідимо її
детальніше.
Розглянемо автономну задачу оптимального керування
 ,
,
Де
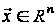 ;
;
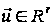 ,
,
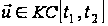 ,
,
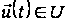 ,
,
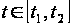 ,
,
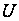 – довільна
множина з
– довільна
множина з
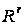 ;
;
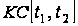 – лінійний
простір кусково-неперервних
на
– лінійний
простір кусково-неперервних
на
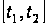 функцій.
функцій.
Крайові умови задачі мають вигляд:
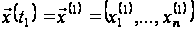 ,
,
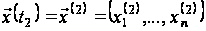 .
.
Потрібно
знайти таке
припустиме
керування
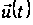 ,
що переводить
систему зі
стану
,
що переводить
систему зі
стану
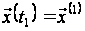 у стан
у стан
 ,
причому відповідний
припустимий
процес
,
причому відповідний
припустимий
процес
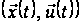 доставляє
мінімальне
значення функціоналу
доставляє
мінімальне
значення функціоналу
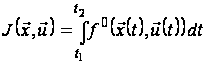 ,
,
де
функції
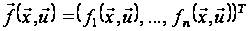 ,
,
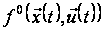 неперервні
по сукупності
всіх змінних
і неперервно-диференційовані
по змінних
неперервні
по сукупності
всіх змінних
і неперервно-диференційовані
по змінних
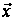 .
.
Вважатимемо,
що функція
Понтрягіна
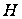 для цієї задачі
є лінійною за
частиною компонент
вектора
для цієї задачі
є лінійною за
частиною компонент
вектора
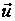 .
Виділимо із
цих компонент
групу з
.
Виділимо із
цих компонент
групу з
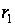 керувань (з
тих, за якими
функція
керувань (з
тих, за якими
функція
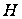 лінійна) і позначимо
їх через
лінійна) і позначимо
їх через
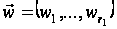 ,
а інші
,
а інші
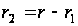 керувань зберемо
у вектор
керувань зберемо
у вектор
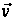 (він також може
включати компоненти,
за якими функція
(він також може
включати компоненти,
за якими функція
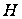 лінійна). За
таких умов
закон руху
набуває вигляду:
лінійна). За
таких умов
закон руху
набуває вигляду:
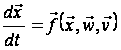 ,
,
де
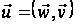 .
.
Складемо функцію Понтрягіна для даної задачі:
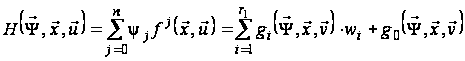 .
.
Очевидно, що
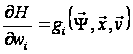 ,
,
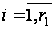 .
(8)
.
(8)
Припустимо,
що процес
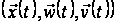 разом з розв’язком
разом з розв’язком
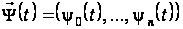 спряженої
системи
спряженої
системи
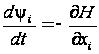 ,
,
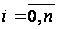 ,
(9)
,
(9)
задовольняє
принципу максимуму
і, крім того,
припустимо,
що у всіх точках
деякого інтервалу
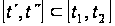 має місце рівність
має місце рівність
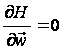 ,
(10)
,
(10)
або, враховуючи (10),
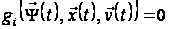 ,
,
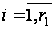 ,
,
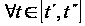 .
(11)
.
(11)
Ця
ситуація означає,
що коефіцієнти
при
 на деякому
часовому відрізку
дорівнюють
0, і оптимальне
керування
визначити
неможливо. У
цьому випадку
вектор керувань
на деякому
часовому відрізку
дорівнюють
0, і оптимальне
керування
визначити
неможливо. У
цьому випадку
вектор керувань
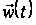 називається
особливим
керуванням
на відрізку
називається
особливим
керуванням
на відрізку
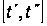 ,
процес
,
процес
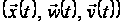 – особливим
режимом, траєкторія
– особливим
режимом, траєкторія
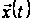 – траєкторією
особливого
режиму, а відрізок
часу
– траєкторією
особливого
режиму, а відрізок
часу
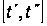 – ділянкою
особливого
керування.
– ділянкою
особливого
керування.
З
формули (11) випливає,
що на ділянці
особливого
режиму функція
Понтрягіна
не залежить
від
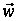 .
Дійсно,
.
Дійсно,
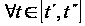 :
:
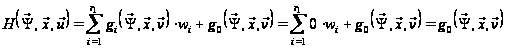 .
.
Тому
в даній ситуації
умова максимуму
по
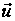 не дає жодної
інформації
про конкретні
значення керувань
не дає жодної
інформації
про конкретні
значення керувань
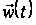 .
.
Оскільки на ділянці особливого режиму має місце співвідношення (11), то очевидно, що
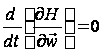 ,
,
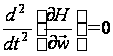
і т.д. Останні співвідношення разом з умовою (10) дозволяють визначити всі особливі режими.
3. Лінійна задача оптимальної швидкодії
Розглянемо лінійну задачу оптимальної швидкодії:
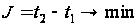 ,
,
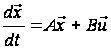 ,
(12)
,
(12)
де
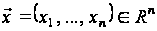 ,
,
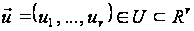 ,
,
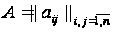 ,
,
 – числові матриці
розмірності
– числові матриці
розмірності
 та
та
 відповідно.
відповідно.
Область
керування
задачі
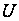 – замкнутий
обмежений
багатогранник
в
– замкнутий
обмежений
багатогранник
в
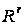 :
:
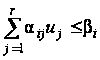 ,
,
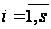 ,
(13)
,
(13)
Якщо
для будь-якого
вектора
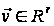 ,
паралельного
будь-якому
ребру багатогранника
,
паралельного
будь-якому
ребру багатогранника
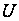 ,
система векторів
,
система векторів
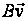 ,
,
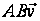 ,
…,
,
…,
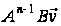 (14) є лінійно
незалежною,
то багатогранник
(14) є лінійно
незалежною,
то багатогранник
 задовольняє
умові спільності
положення
відносно системи
(14).
задовольняє
умові спільності
положення
відносно системи
(14).
Для перевірки лінійної незалежності векторів (13) достатньо перевірити, чи матриця, стовпцями якої є стовпці (12), є невиродженою, тобто
 .
.
Перепишемо формулу (10):
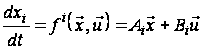 ,
,
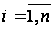 ,
,
де
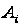 ,
,
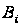 –
–
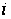 -і
рядки матриць
-і
рядки матриць
 і
і
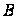 .
.
Функція Понтрягіна лінійної задачі оптимальної швидкодії має вигляд:
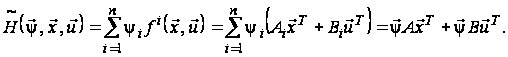 (15)
(15)
Оскільки
перший доданок
у формулі (15) не
залежить від
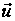 ,
то функція
,
то функція
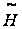 досягає максимуму
за змінною
досягає максимуму
за змінною
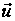 одночасно з
функцією
одночасно з
функцією
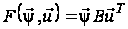 .
.
Спряжена система у цьому випадку може бути записана у вигляді:
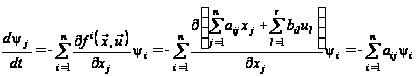 ,
,
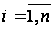 ,
,
або у векторній формі
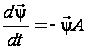 .
(16)
.
(16)
Позначимо
через
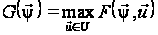 .
З теореми 2
.
З теореми 2
