Лекции по Математическому анализу
/>Произведение бесконечно больших на ф-ию, имеющую отличный от нуля предел - бесконечно большая.
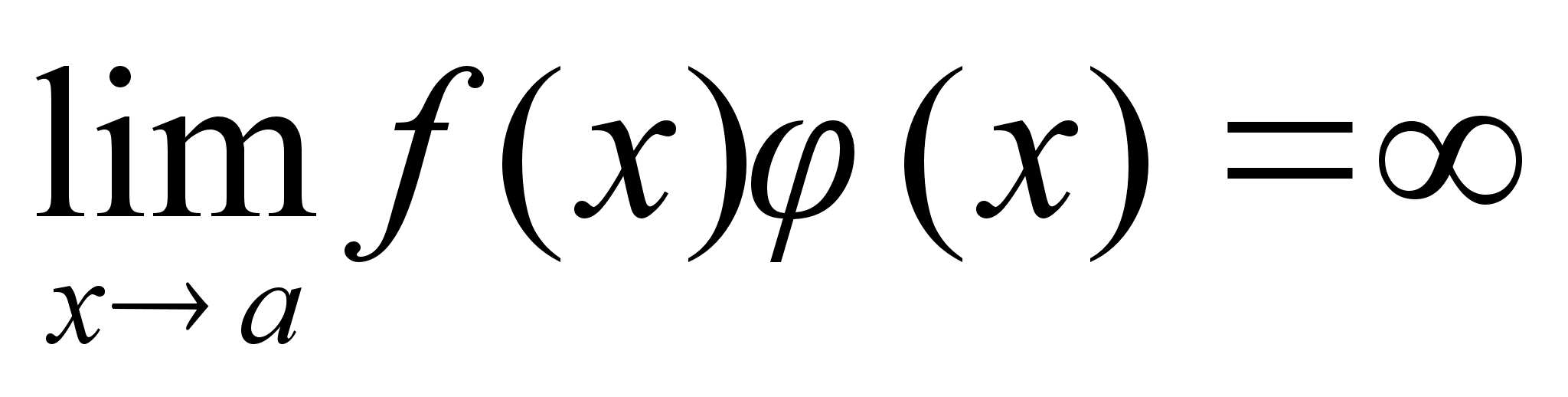
Ф-ия, обратная величине бесконечно большой – есть бесконечно малая, и наоборот.
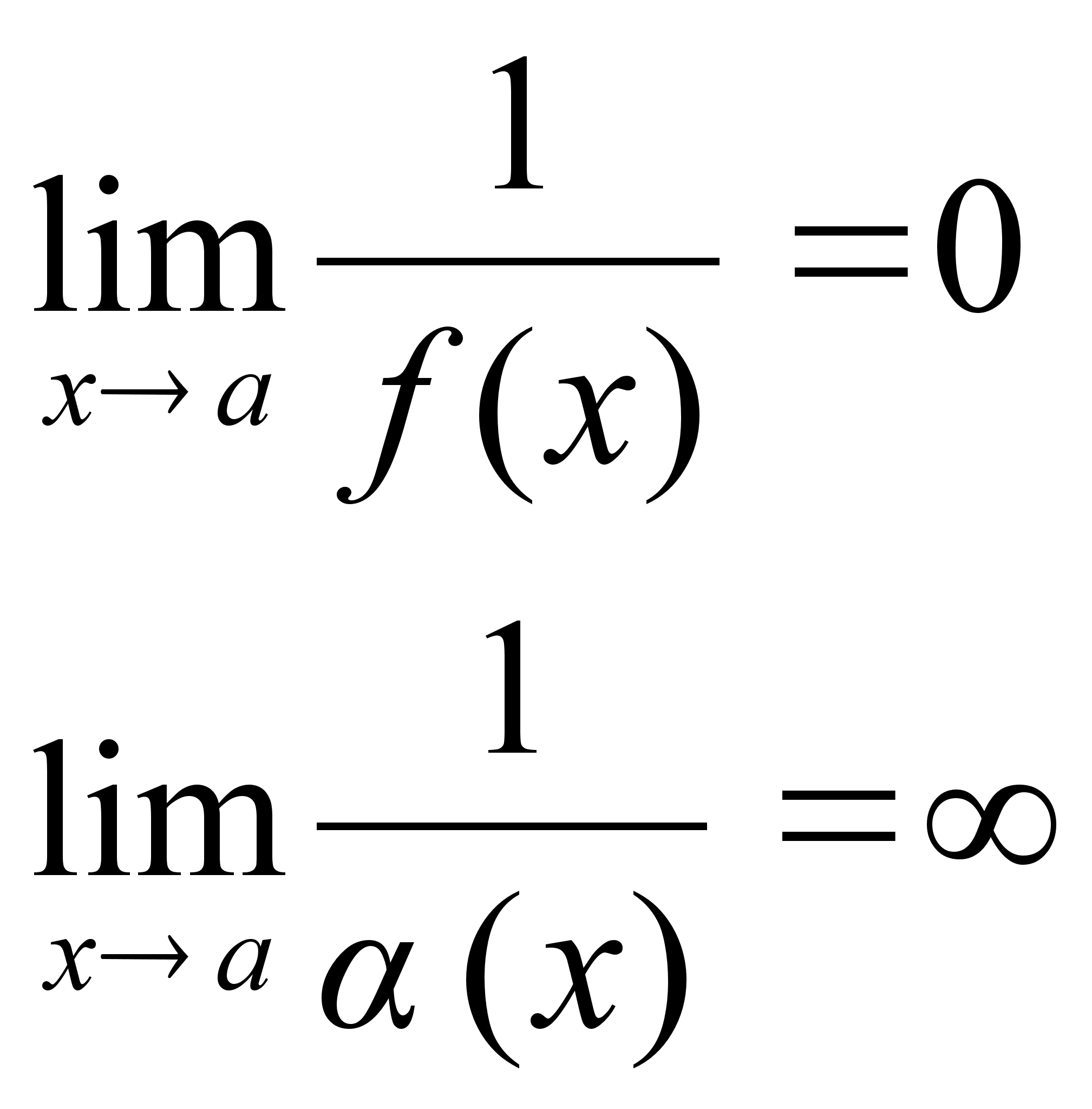
Доказательство 2):
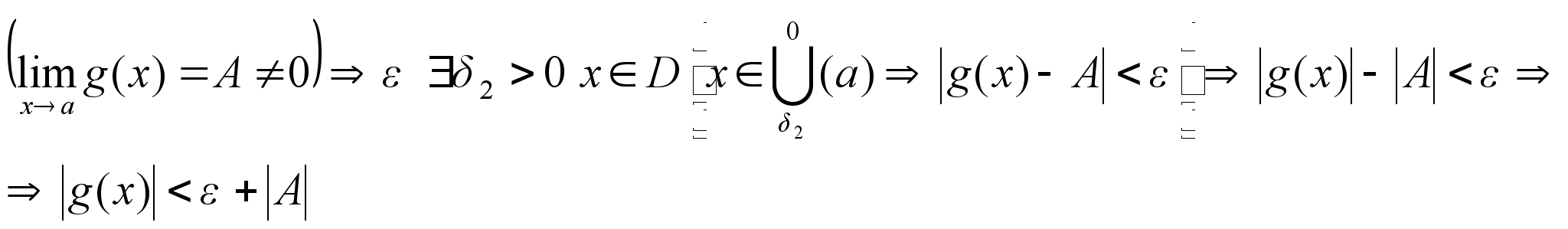
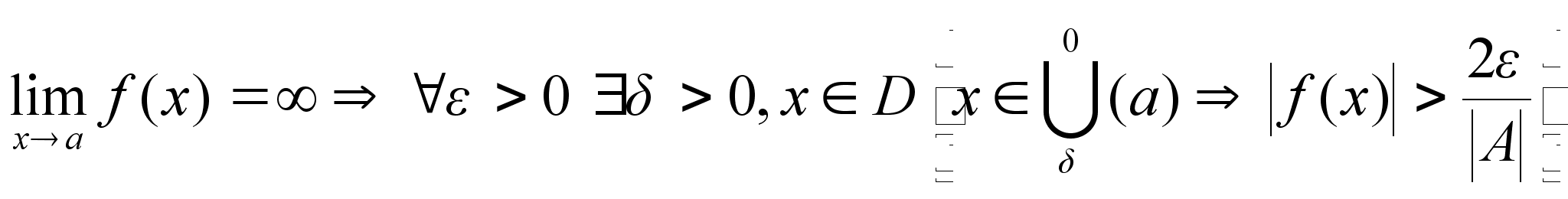
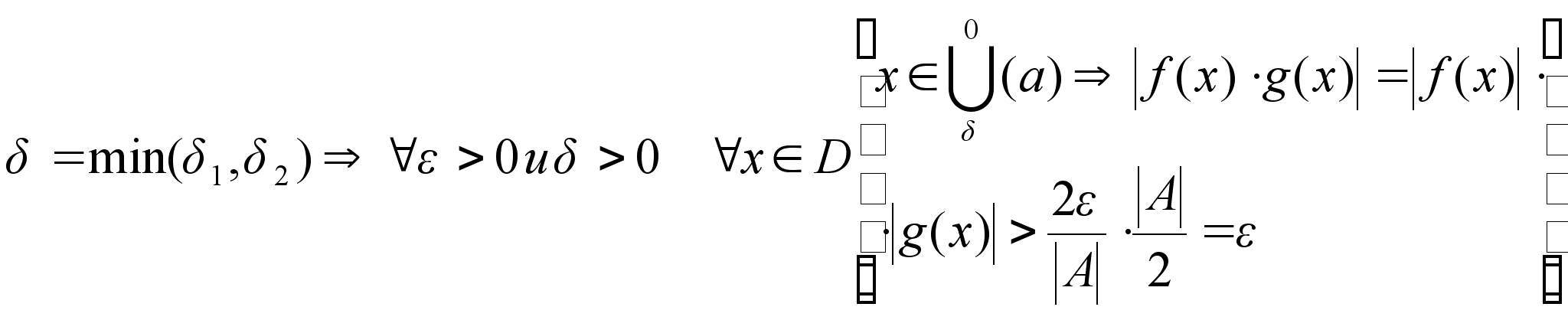

Доказательство 3):
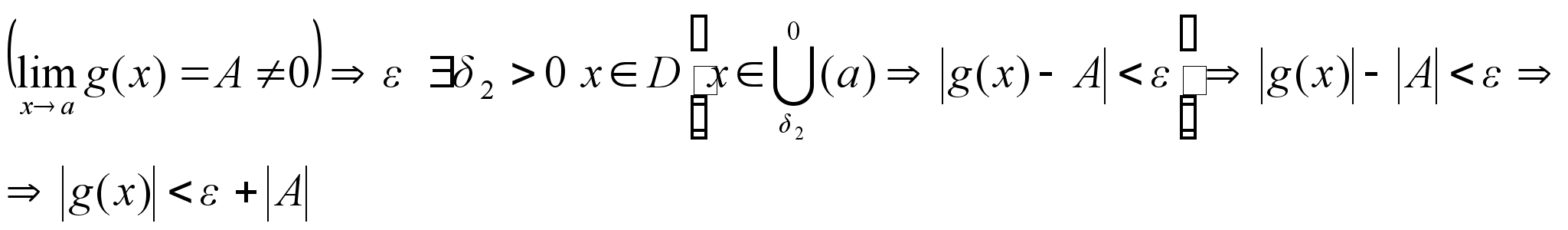
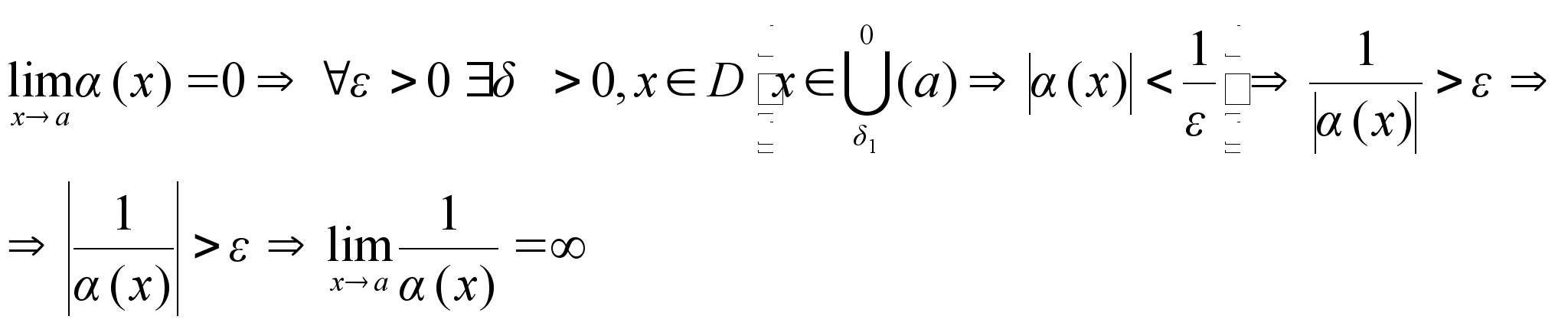
Односторонние пределы в конечной точке и их связь с пределом в этой точке.
В определении предела окрестности точки а – симметричный интервал с центром в этой точке, т.е. требуется существование значений ф-ий как справа от точки а , так и слева от нее.
Когда а – граничная точка D(f)- такая ситуация невозможна. В этом, случае вводится понятие одностороннего предела, в определении которого фигурирует левые и правые полуокрестности точки а
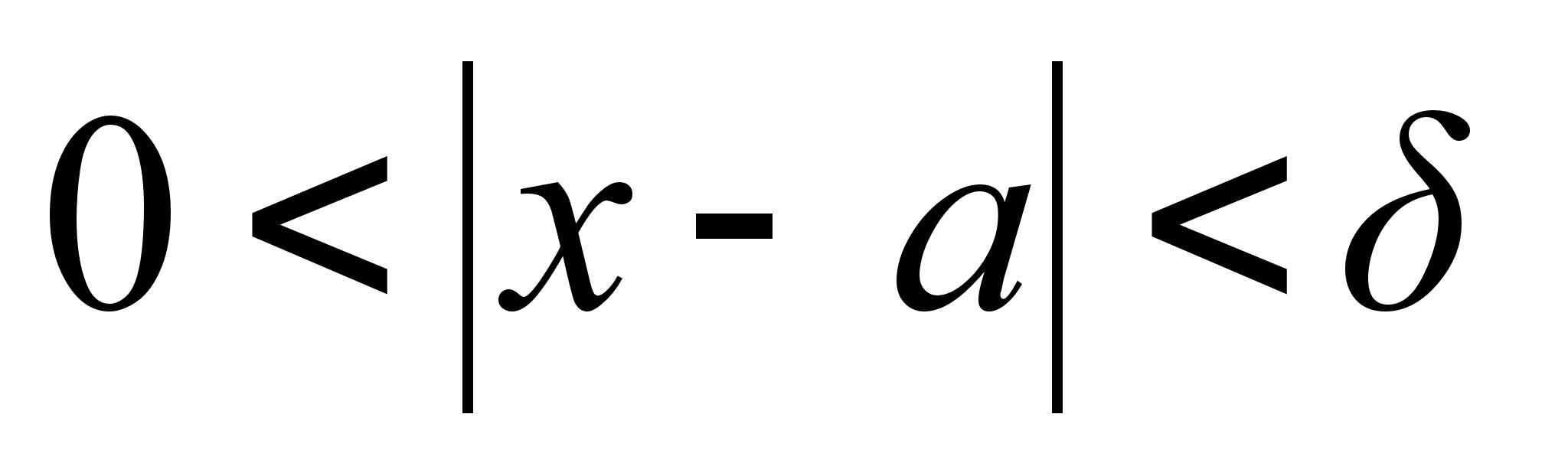
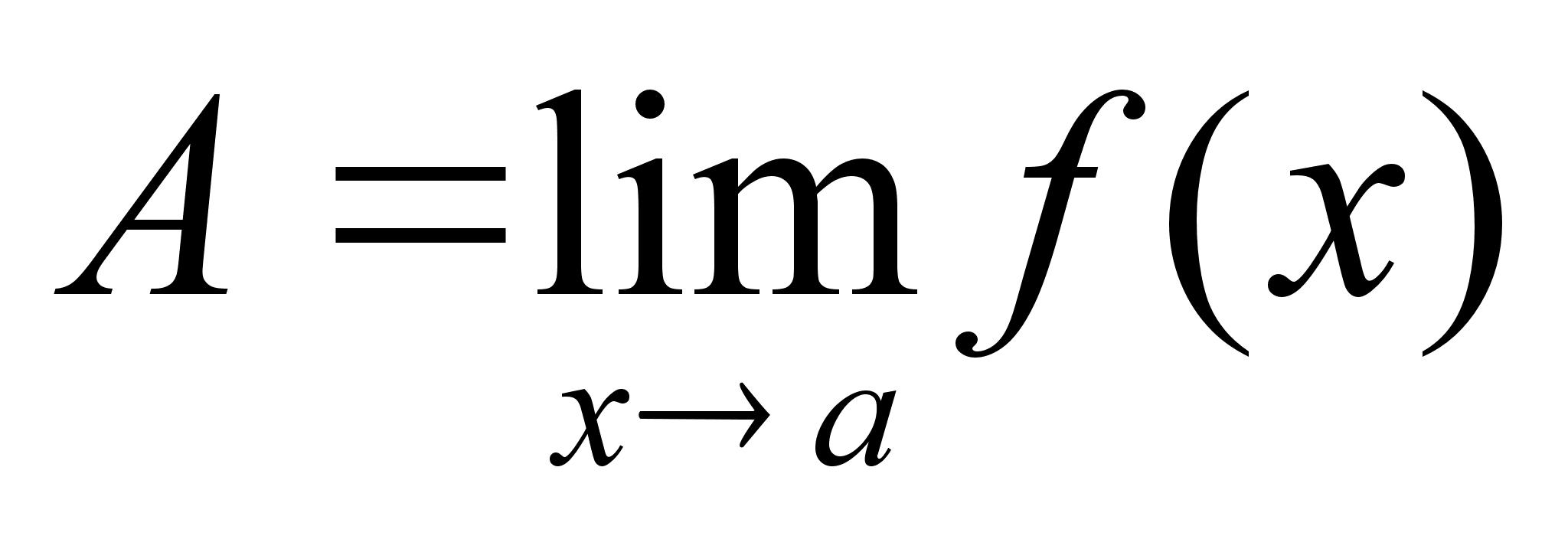 -
левосторонний
предел, если
-
левосторонний
предел, если
 в
левой
полуокружности
точки А,
значения ф-ии
лежат в -окрестности
точки А
в
левой
полуокружности
точки А,
значения ф-ии
лежат в -окрестности
точки А
Аналогично дается определение правостороннего предела.
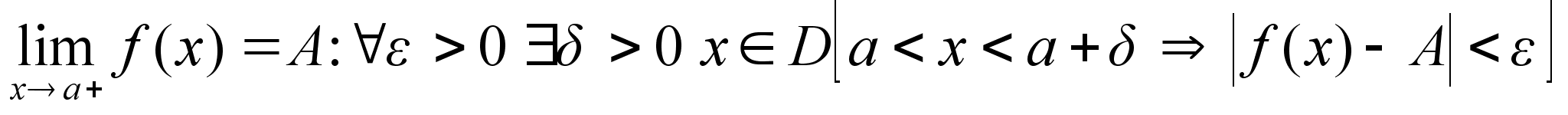
Теорема: Для того, чтобы в точке а существовал предел ф-ии, необходимо и достаточно существования и равенства левостороннего и правостороннего пределов
Доказательство:
Необходимость:
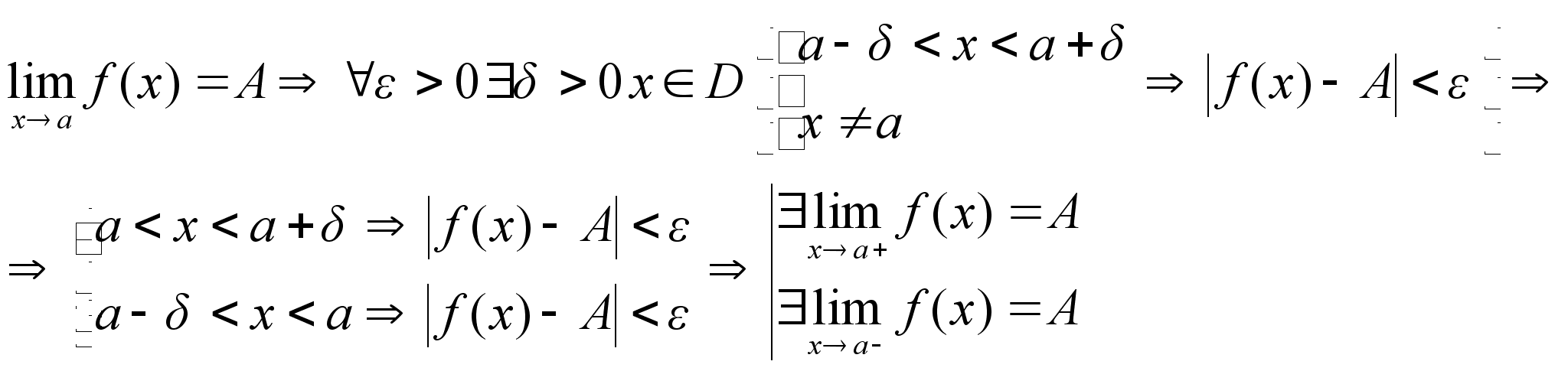
Достаточность:
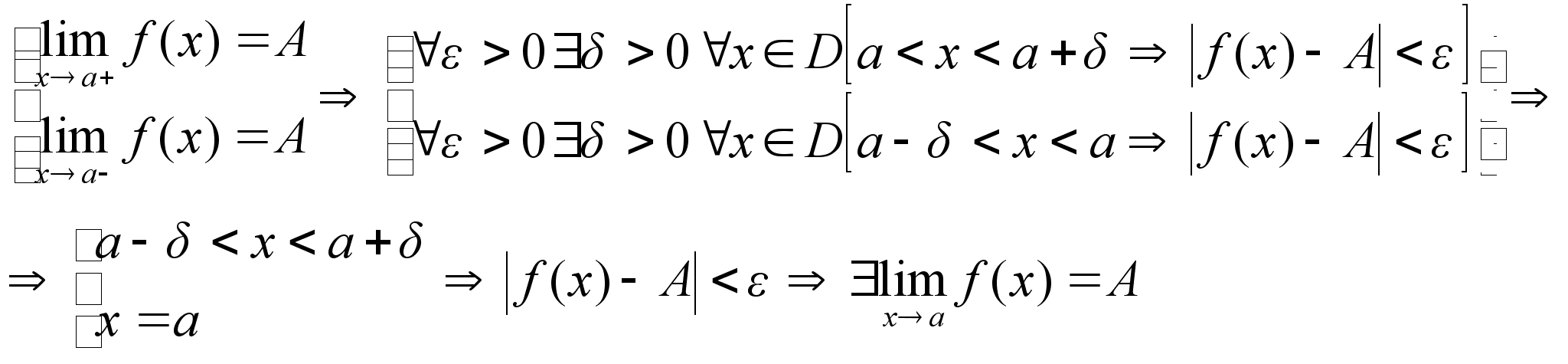
Числовые последовательности
Задача, по которой каждому N числу, ставится в соответствие единственное вещественное число – называется числовой последовательностью.
Числовая последовательность – ф-ия натурального аргумента.
Обозначается:
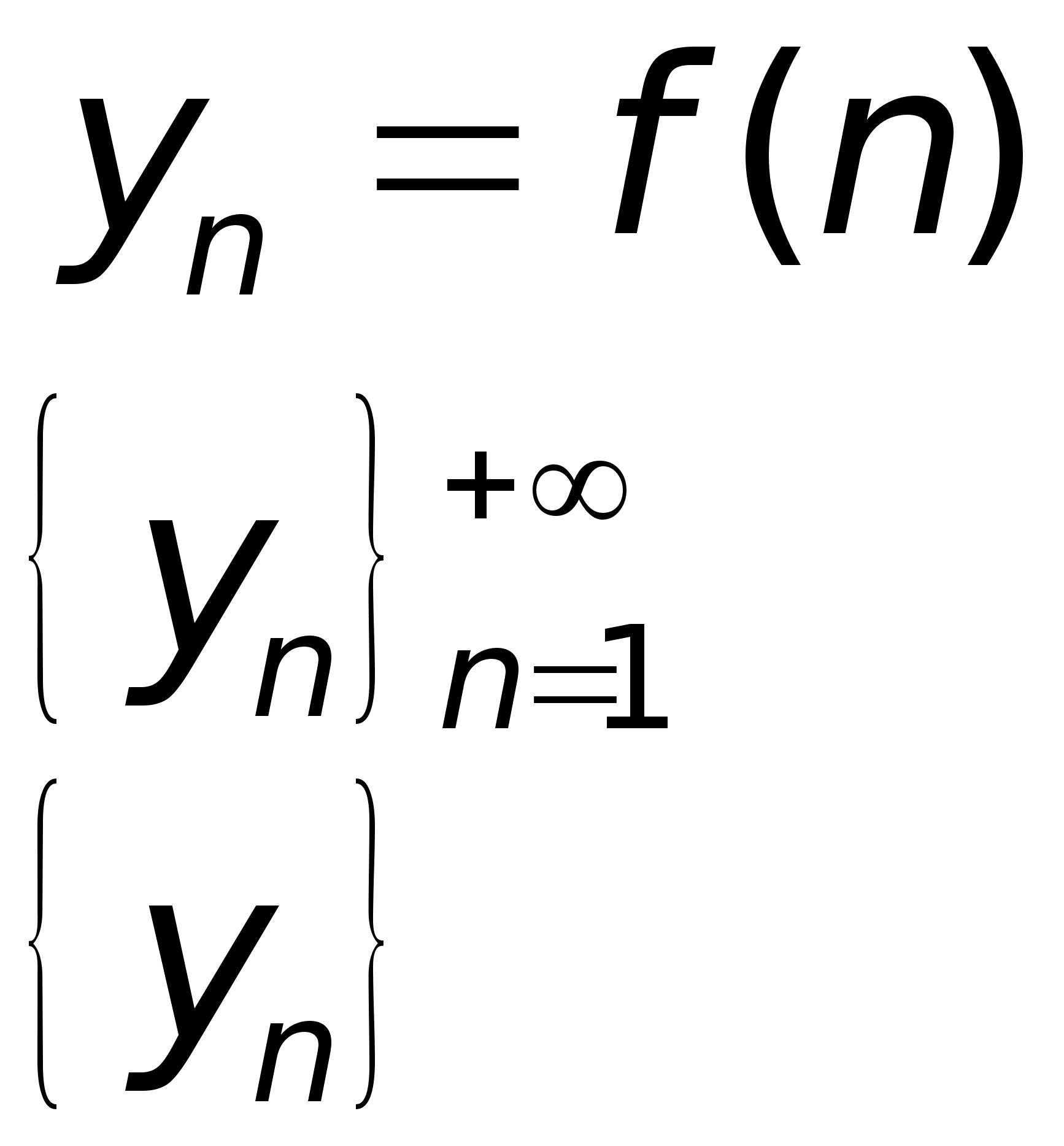
Последовательность, множество значений которой состоит из одного числа – стационарная.
Так как числовая последовательность – не симметричное множество, то для него не существует понятия четности, нечетности, периодичности. Зато сохраняются свойства, связанные с упорядоченностью.
Свойства:
Ограниченность.
последовательность
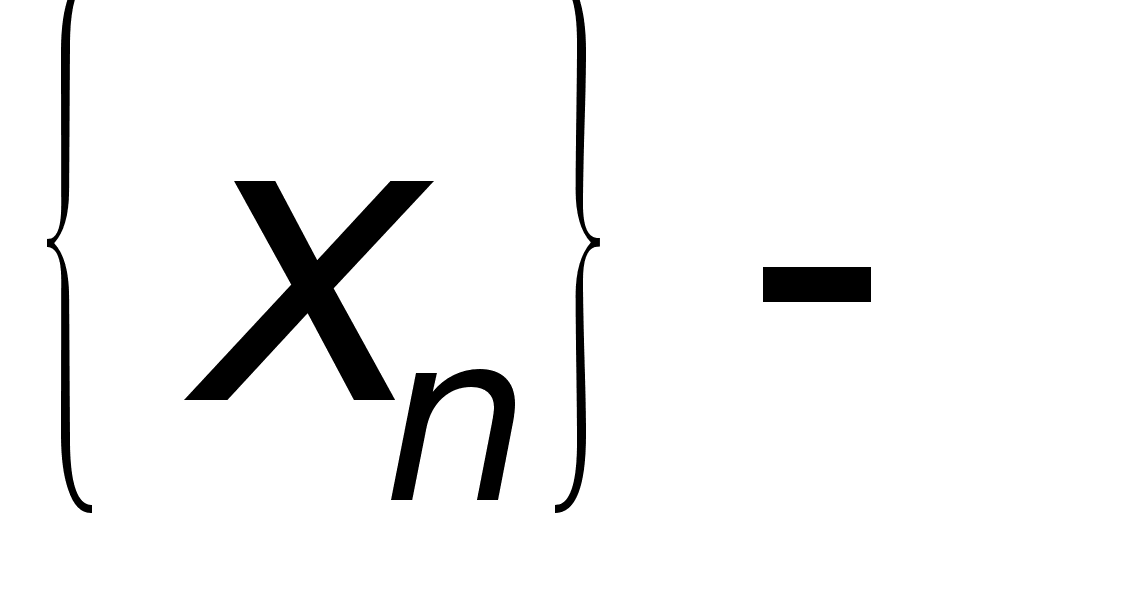 ограничена
сверху, если
ограничена
сверху, если
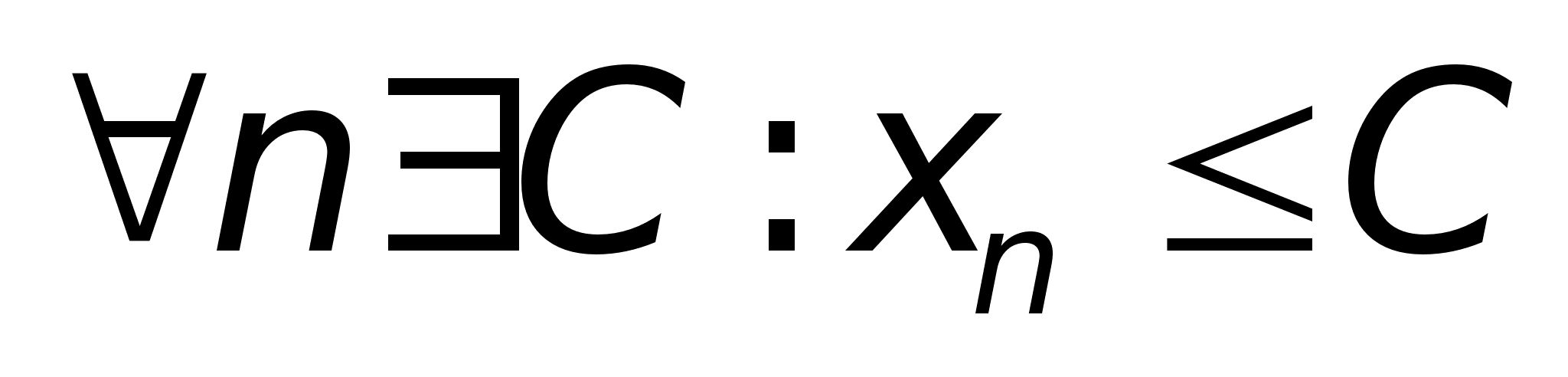
последовательность
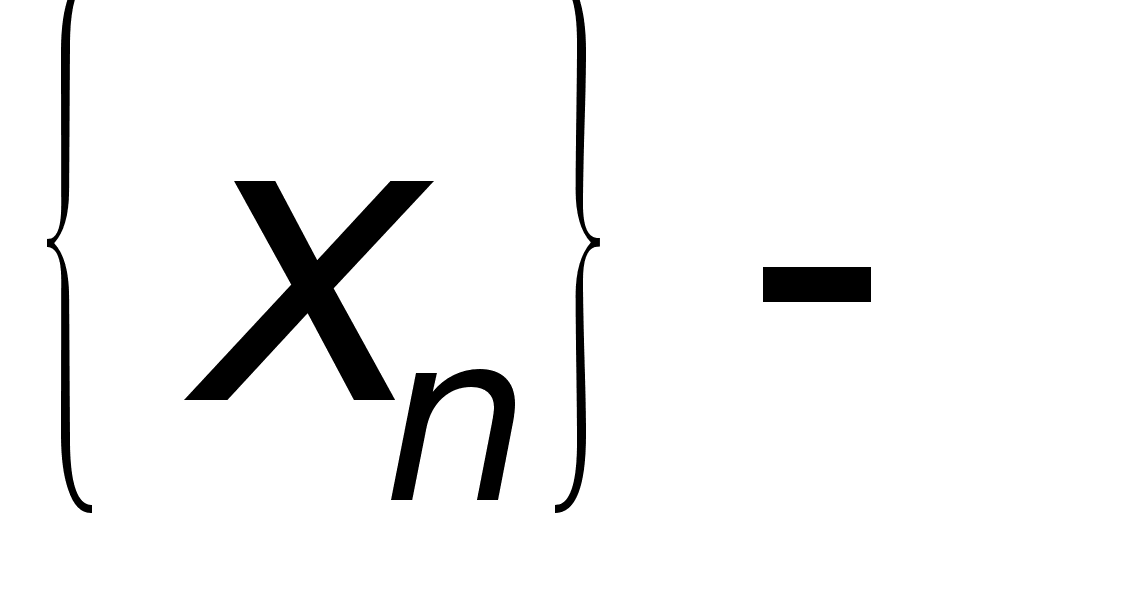 ограничена
снизу, если
ограничена
снизу, если
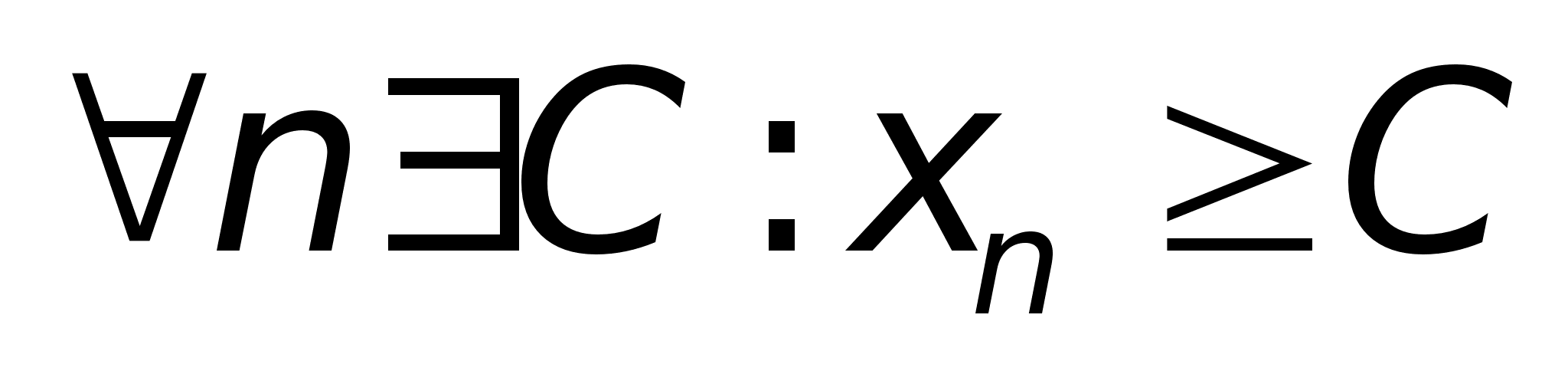
последовательность
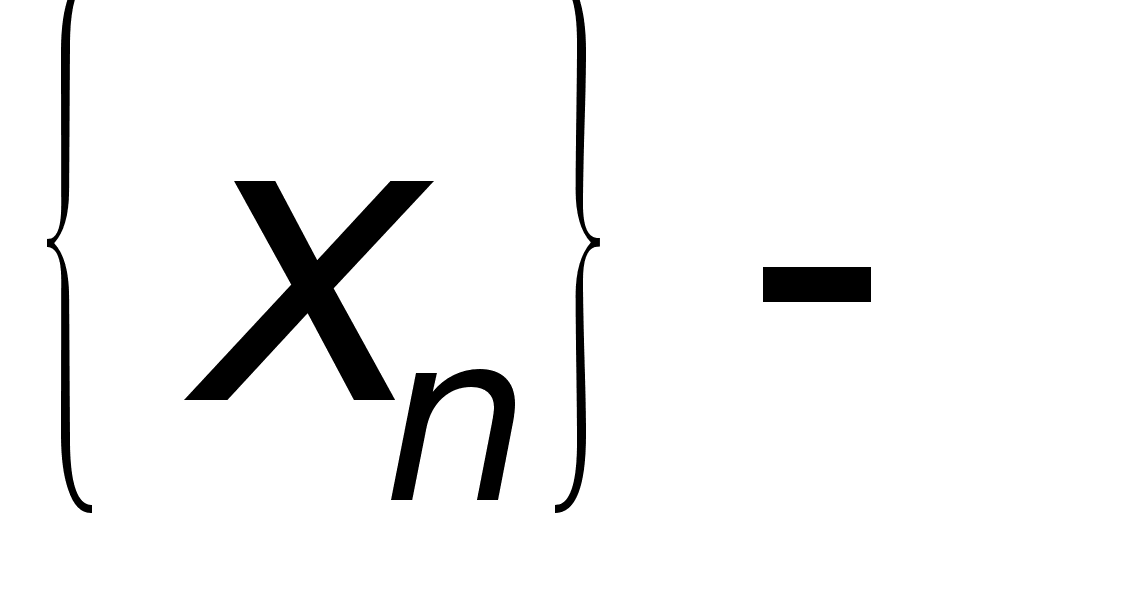 ограничена,
если
ограничена,
если

Монотонность.
последовательность
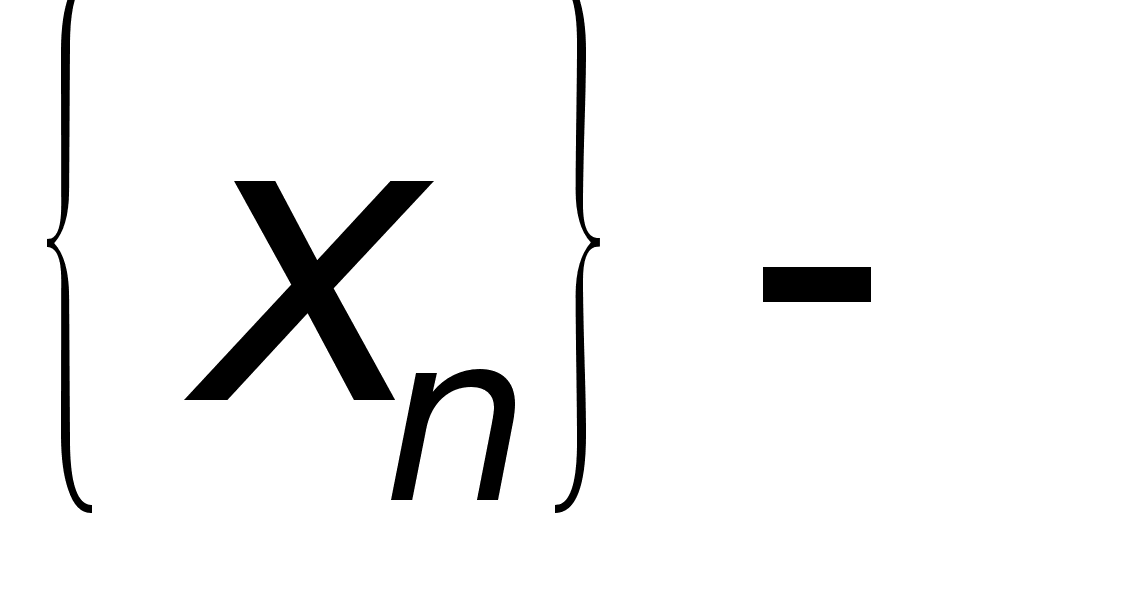 возрастает,
если
возрастает,
если
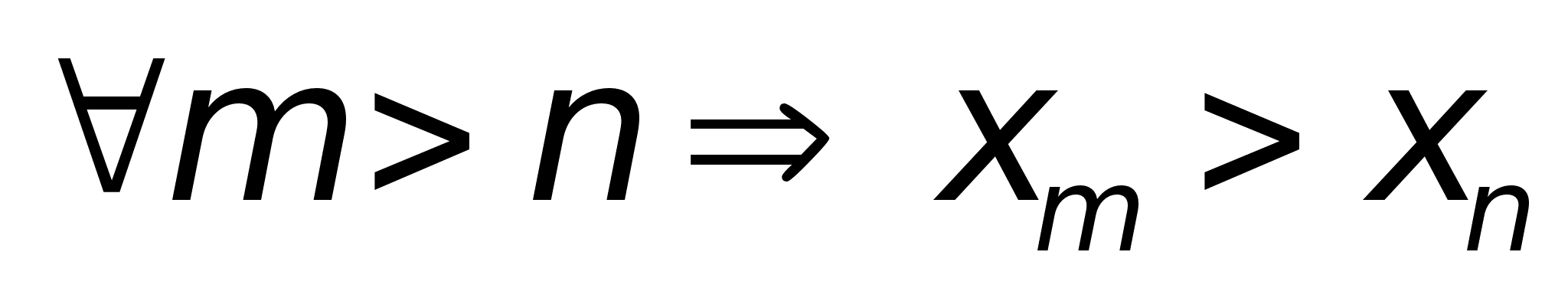
последовательность
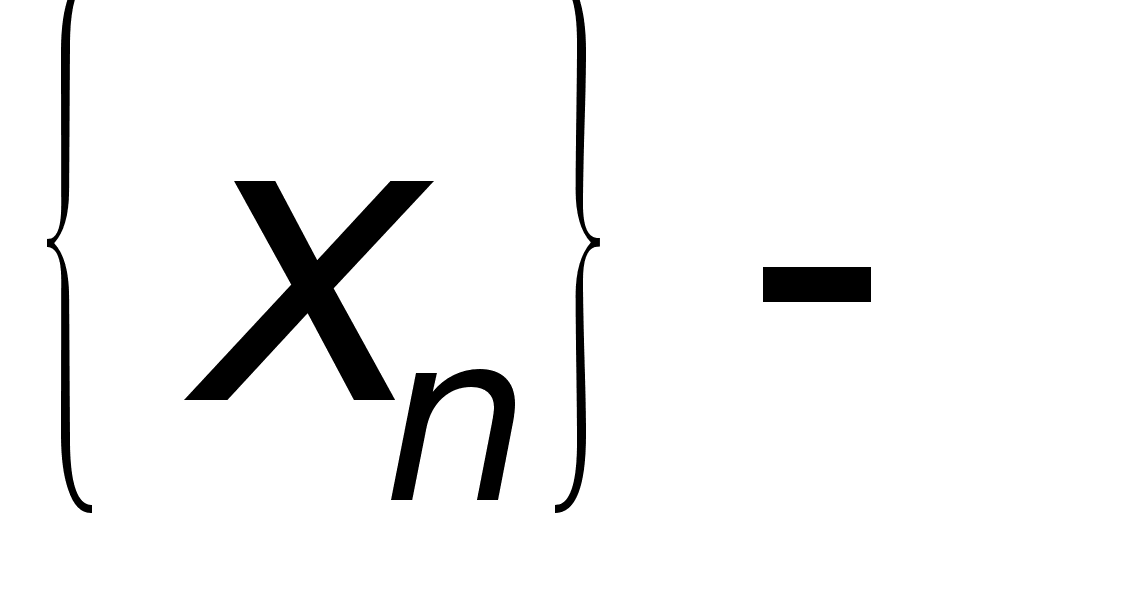 убывает,
если
убывает,
если

последовательность
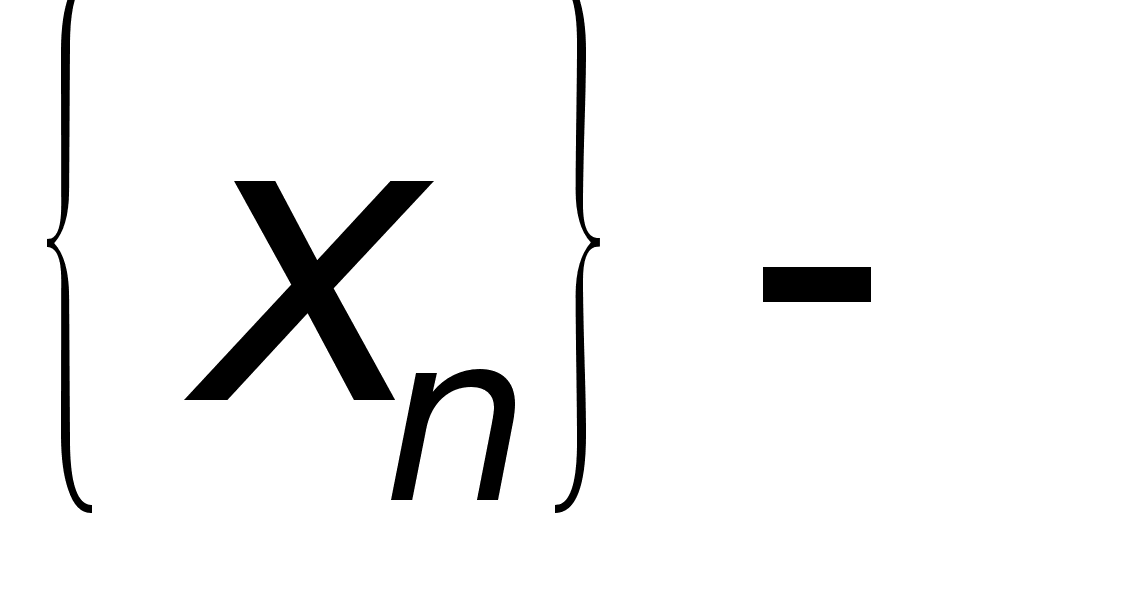 не
убывает, если
не
убывает, если

последовательность
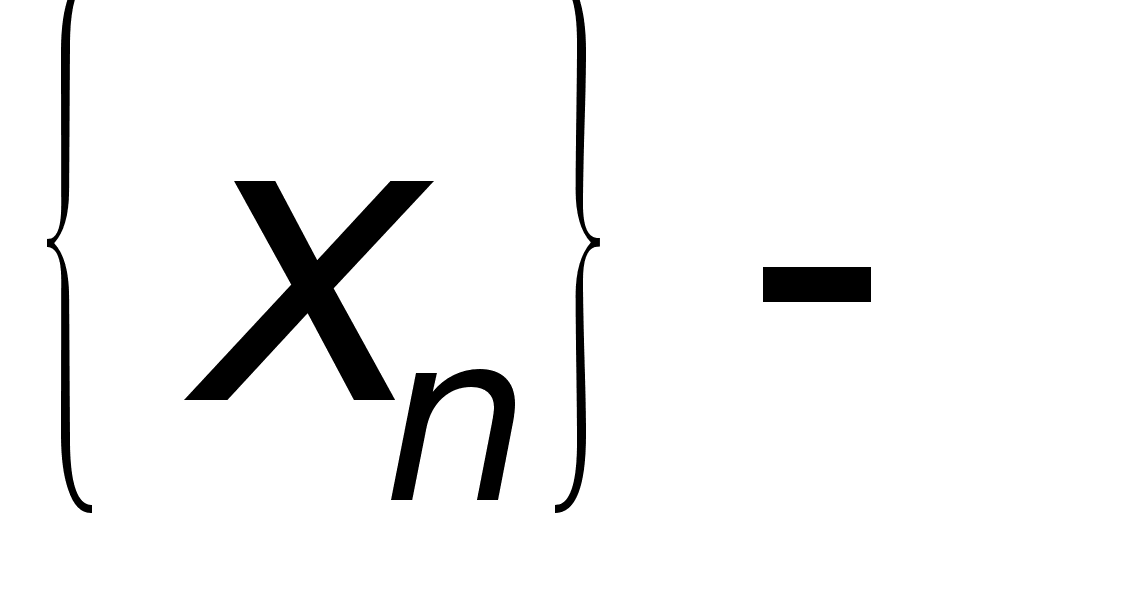 не
возрастает,
если
не
возрастает,
если
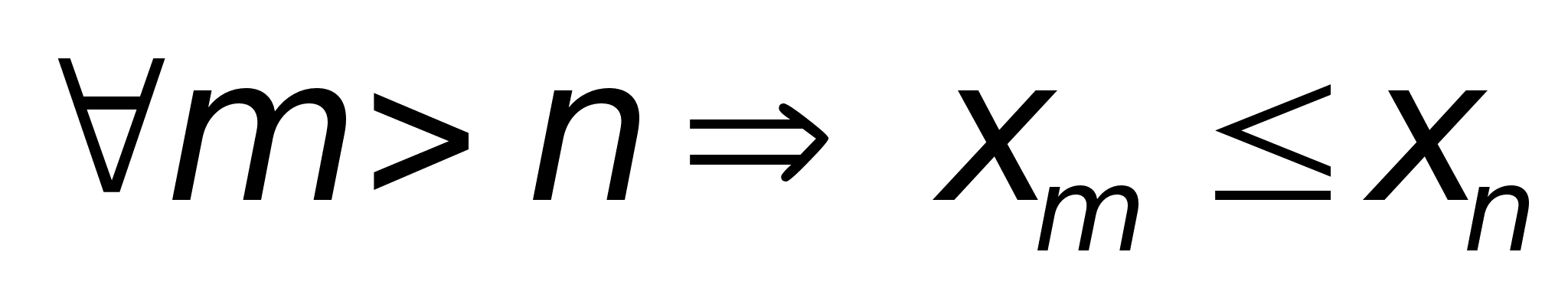
Предел последовательности
Т.к.
N числа
имеет 1 т. бесконечности,
то для числовой
последовательности
существует
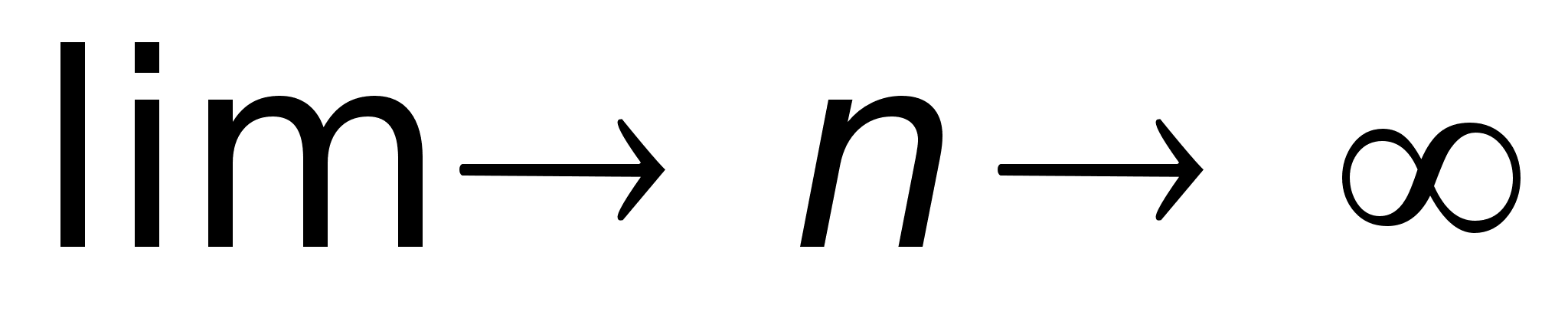

Замечания:
А может быть конечным или бесконечным
Если последовательность имеет конечный предел, то она называется сходящейся, а если нет – расходящейся.
Общие свойства сходящихся последовательностей аналогичны свойствам ф-ий, имеющих конечный предел.
Арифметические свойства сходящихся последовательностей аналогичны свойствам ф-ий, имеют конечный предел
Переход к пределам в неравенствах, для сходящихся последовательностей аналогичен ф-ям, имеющим конечный предел.
Определение бесконечно малых и бесконечно больших последовательностей и их свойства аналогичны соответствующим определениям и свойствам ф-ии непрерывного аргумента.
Критерии существования предела последовательности
1. Критерии Коши (произведения последовательностей)
Для
существования
предела последовательностей
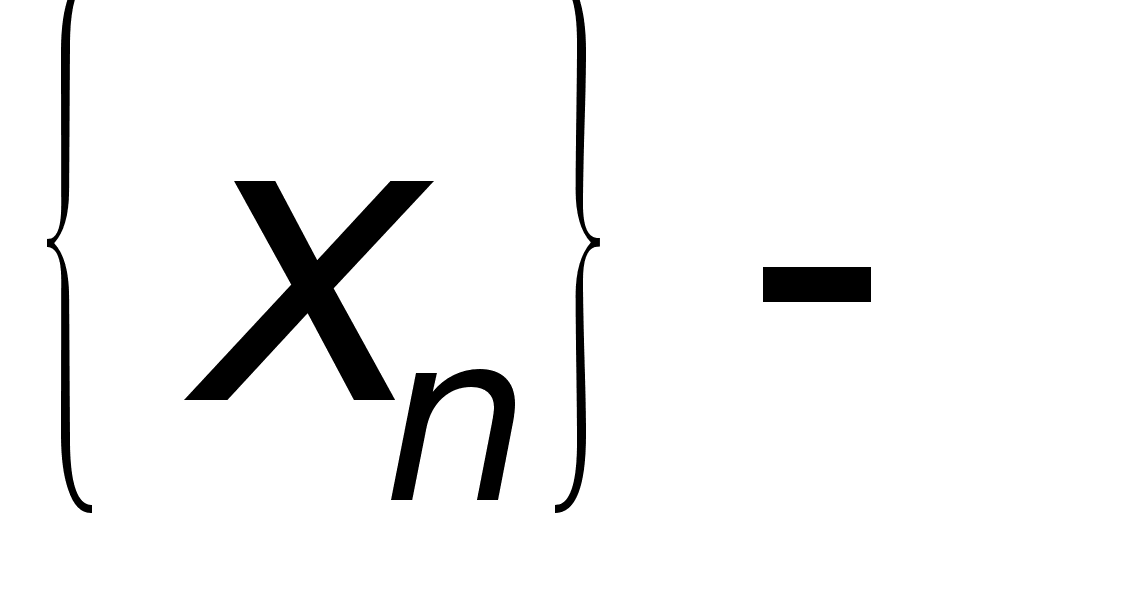 необходимо
и достаточно,
чтобы для
любой..............
необходимо
и достаточно,
чтобы для
любой..............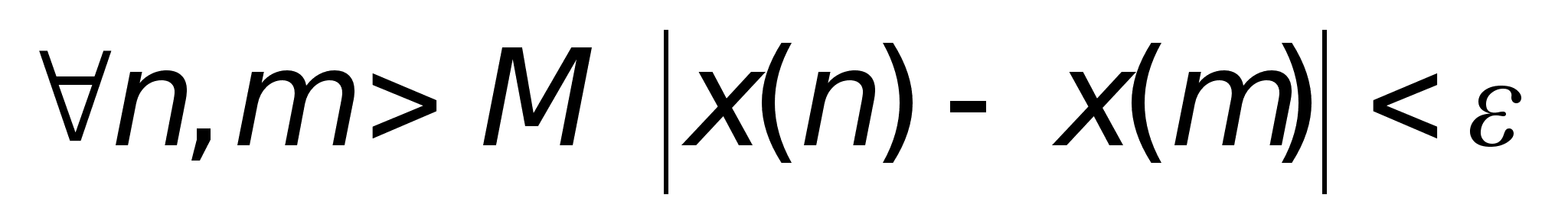
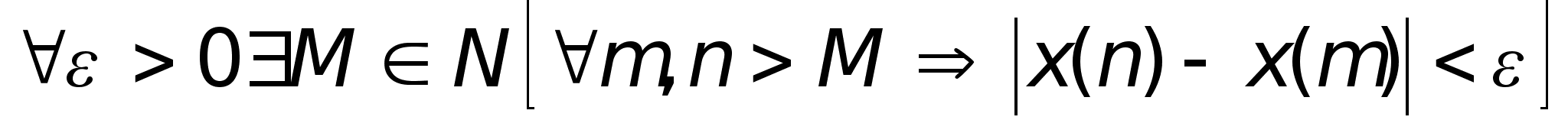
Последовательность, для которой выполняется признак Коши – фундаменталная
2. Критерий Вейерштрасса (монотонность последовательности)
а) неубывающие последовательности, ограниченные сверху, имеют предел.
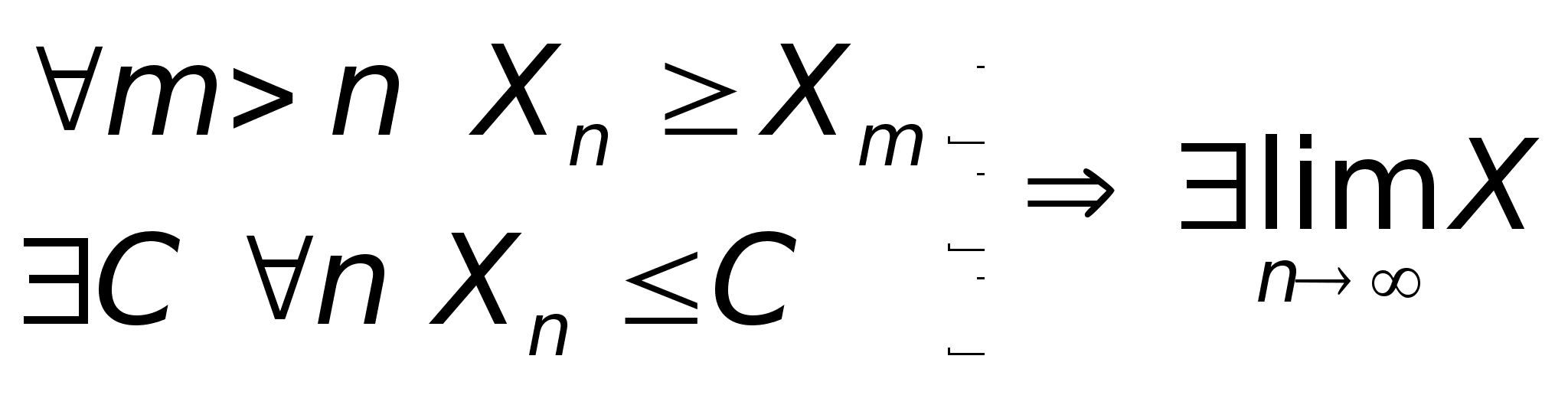
б) не возрастающие последовательности, ограниченные снизу, имеют предел.
Доказательство(а):
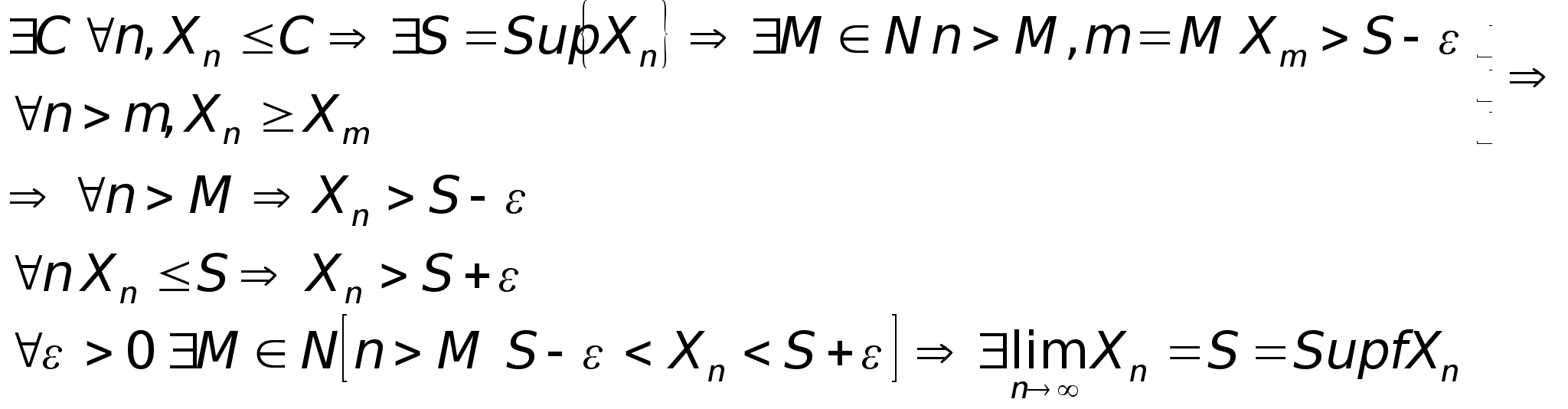
Переход к пределу в неравенстве
Теорема: Пусть f(х) и (х) имеют конечные пределы в т. y=a, тогда справедливо:
Доказательство:
Пусть
 ,
тогда по общему
свойству №6
,
тогда по общему
свойству №6
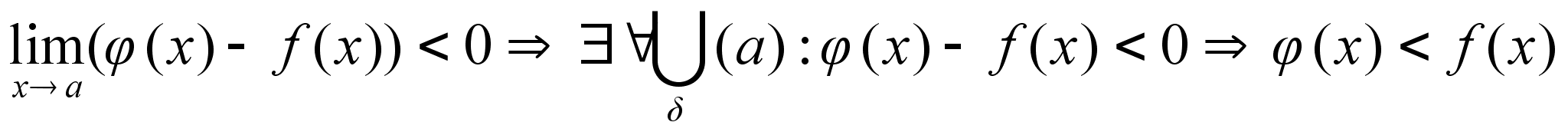 ,
,
а это противоречит 1
Замечание:
Из утверждения №3 следует, что предел неотрицательной ф-ии является неотрицательным.
При пределов к противоположным можно обе части умножать на (-1).
Теорема
2(о двух миллиционерах
) Пусть в некоторой
области Д выполняется
система неравенств
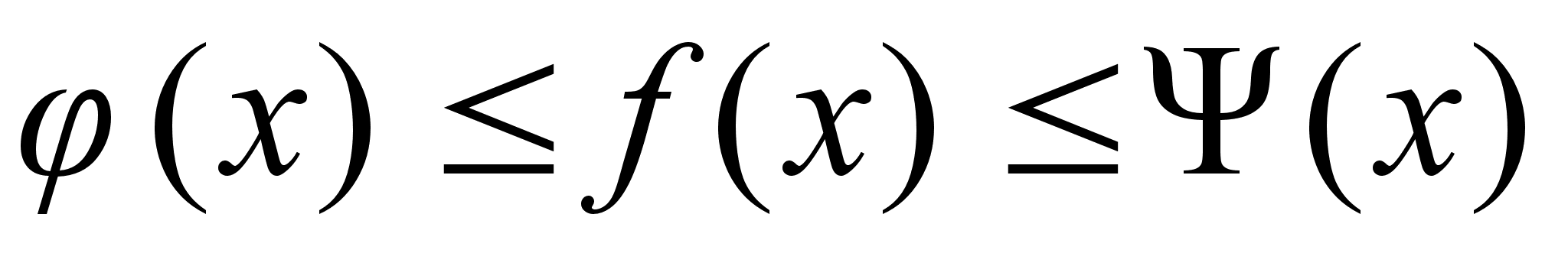 и а – предел
точки.
и а – предел
точки.
Пусть
существуют
равные пределы
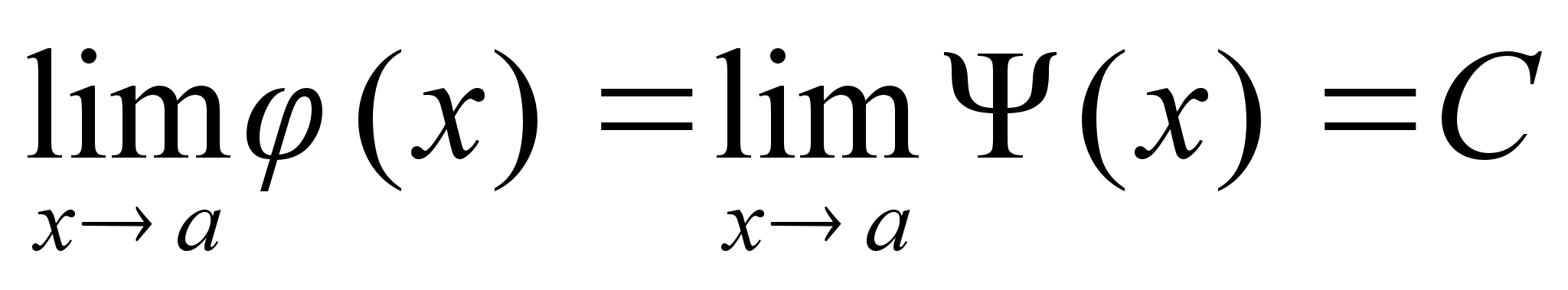 ,
,
тогда
существует
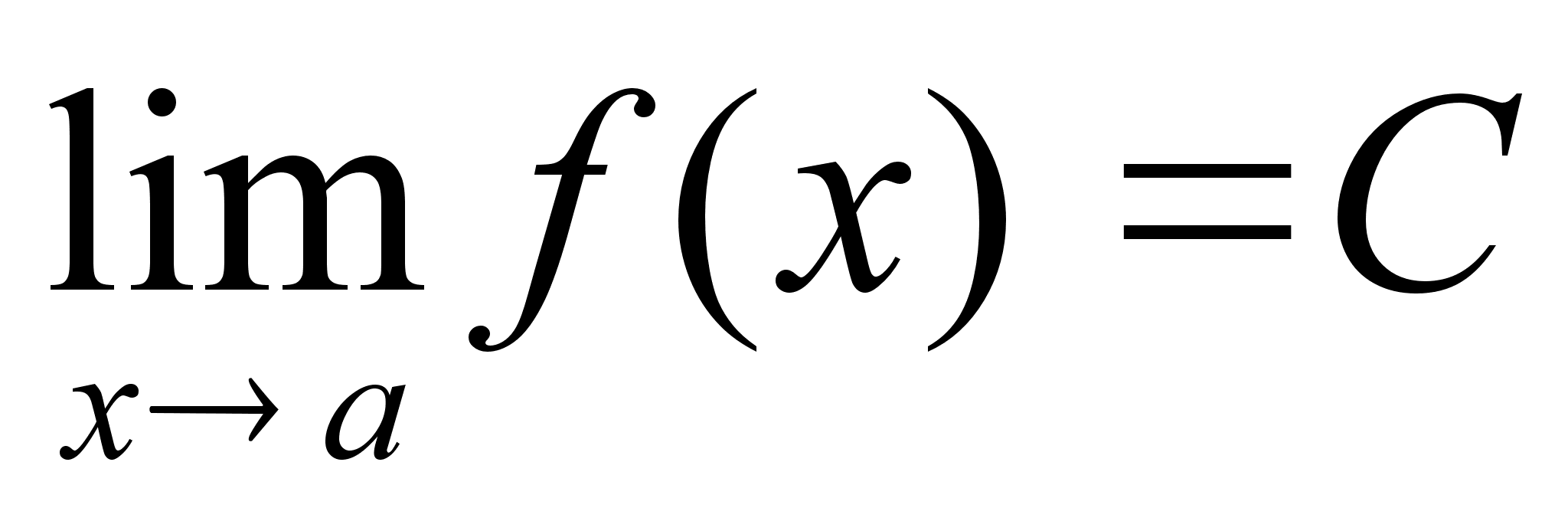 .
.
Доказательство:
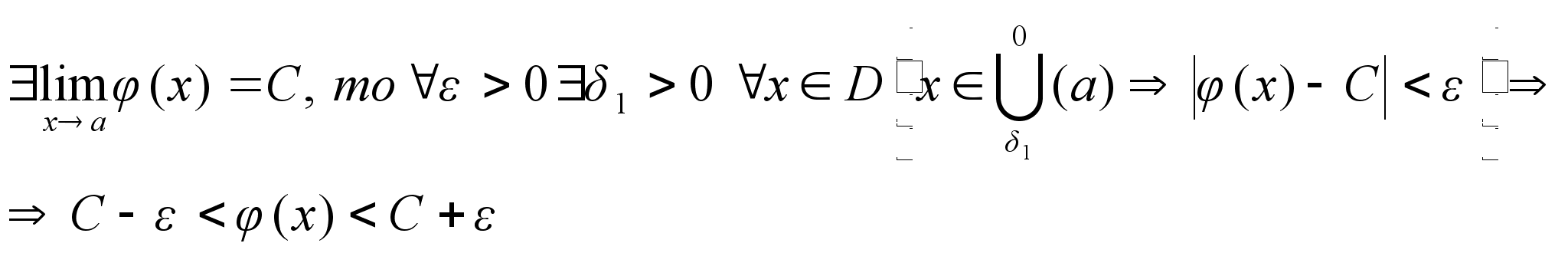

Первый замечательный предел
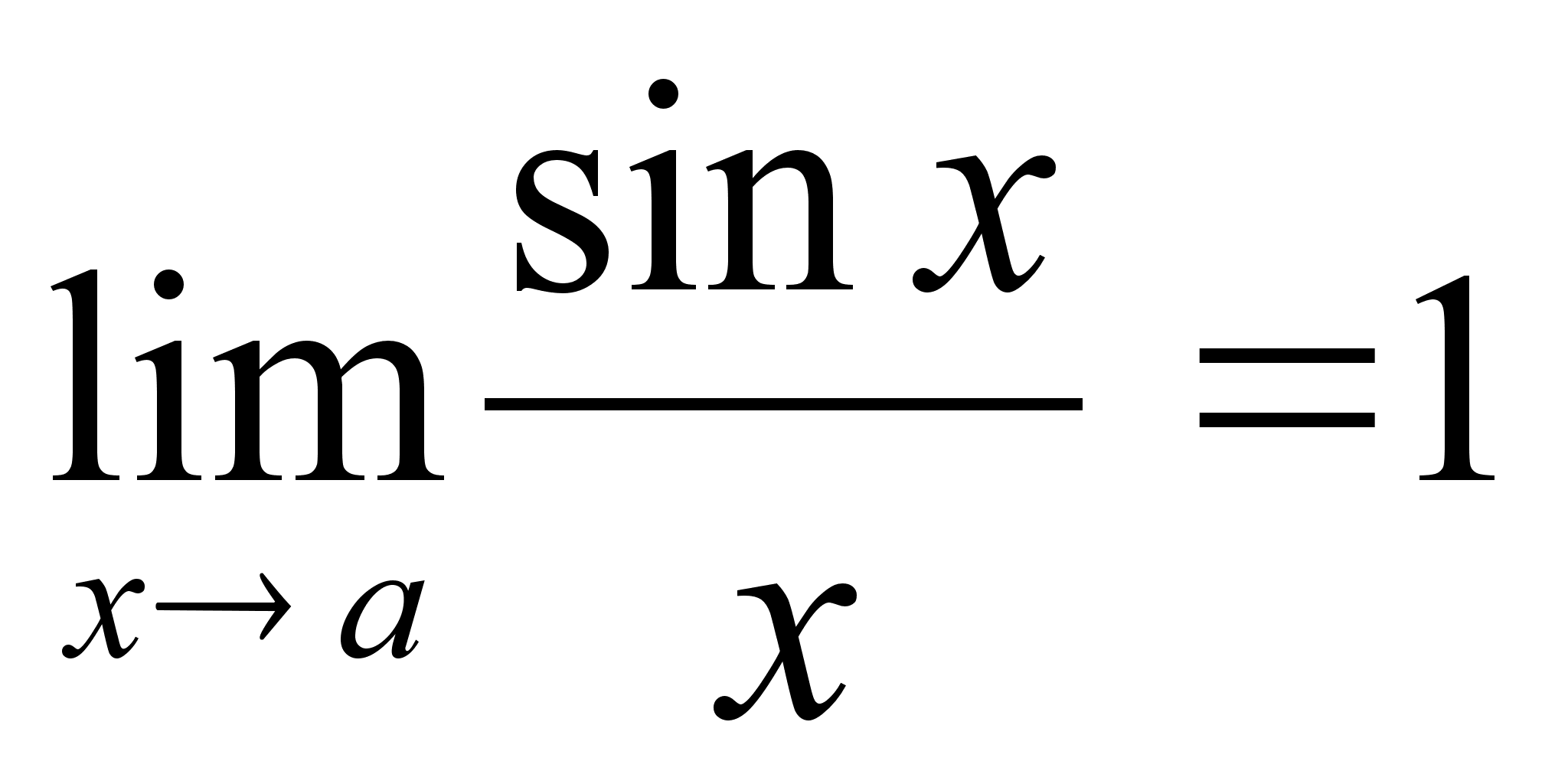
Д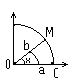 оказательство:
докажем для
оказательство:
докажем для
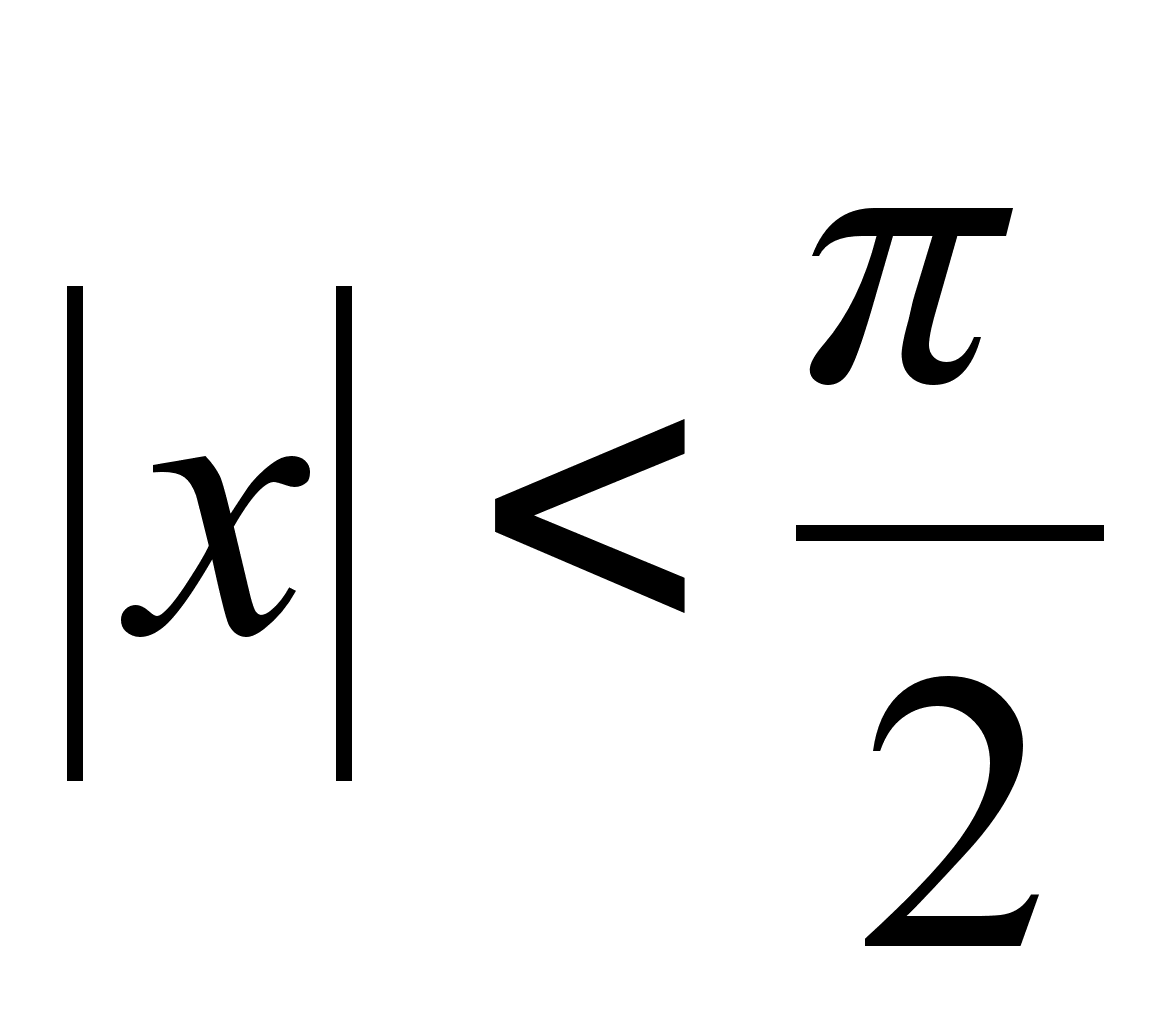 справедливость
неравенства
справедливость
неравенства

В силу
четности входящих
в неравенство
ф-ий, докажем
это неравенство
на промежутке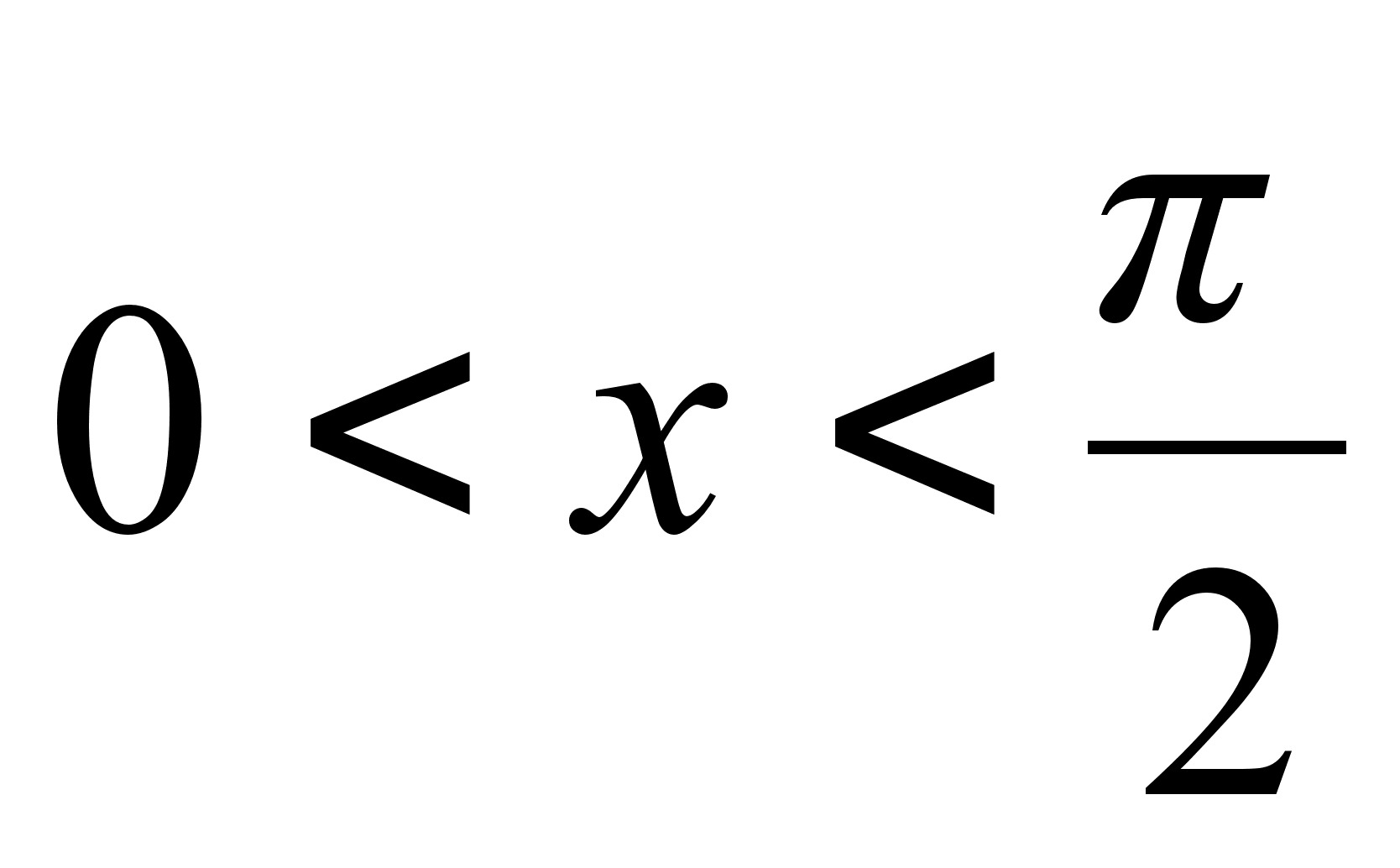
Из рисунка видно, что площадь кругового сектора
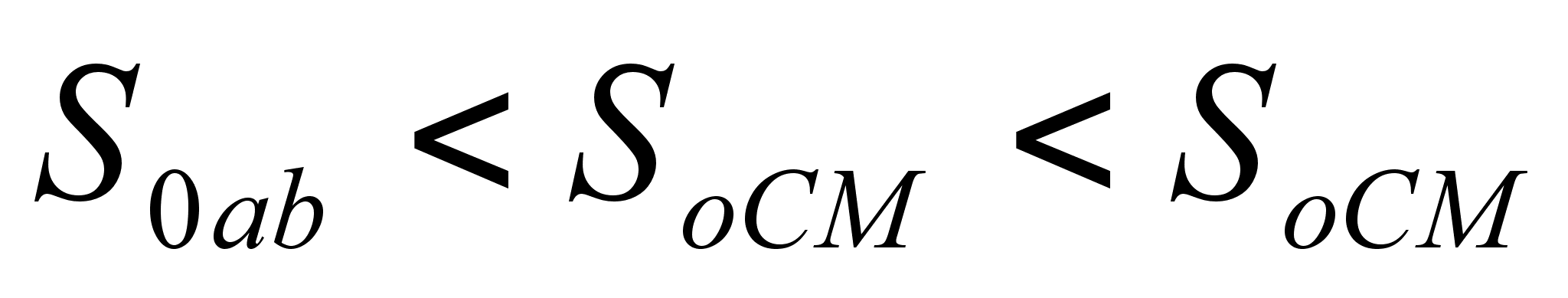
 ,
так как х>0, то
,
так как х>0, то
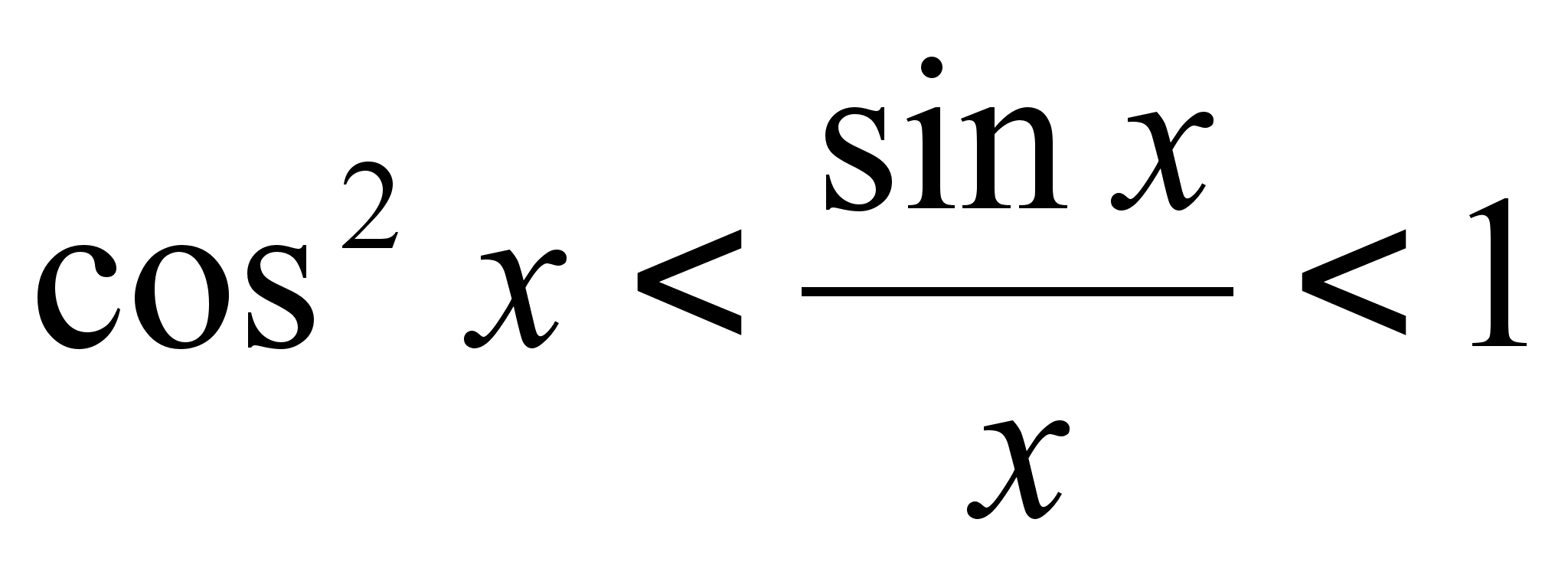 ,
,
2. следовательно,
что


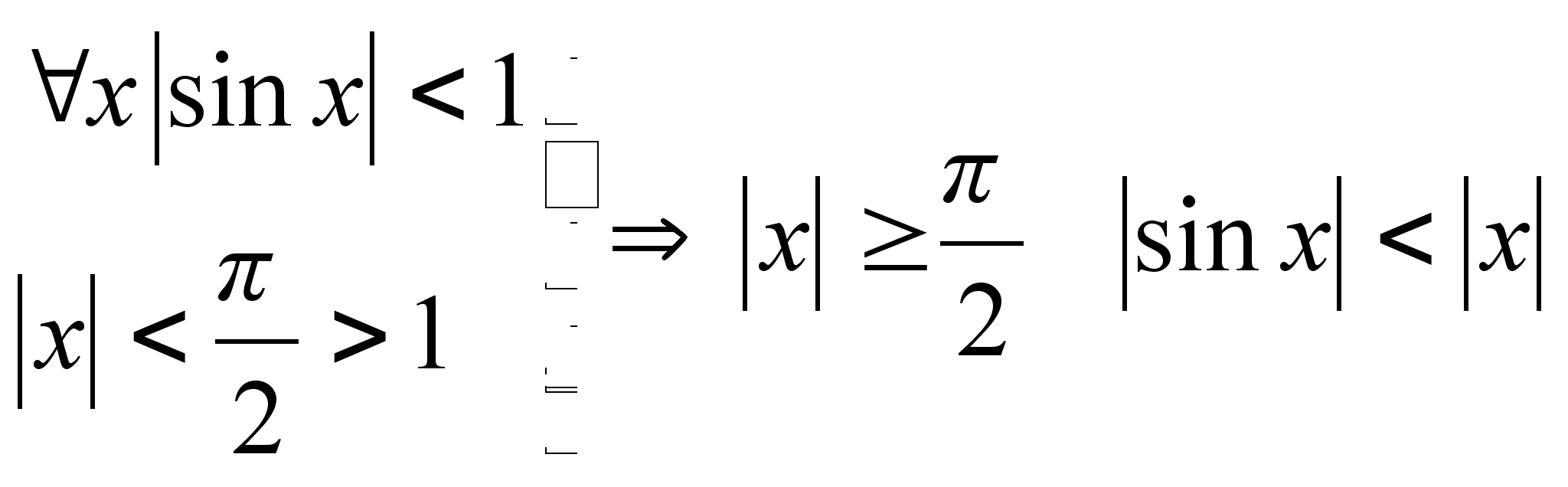
Покажем, что
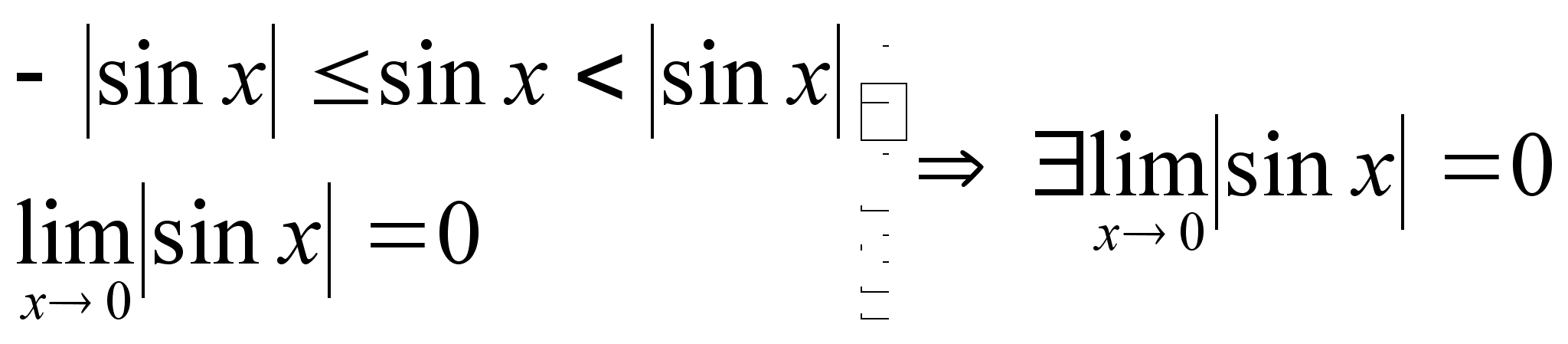
Докажем, что
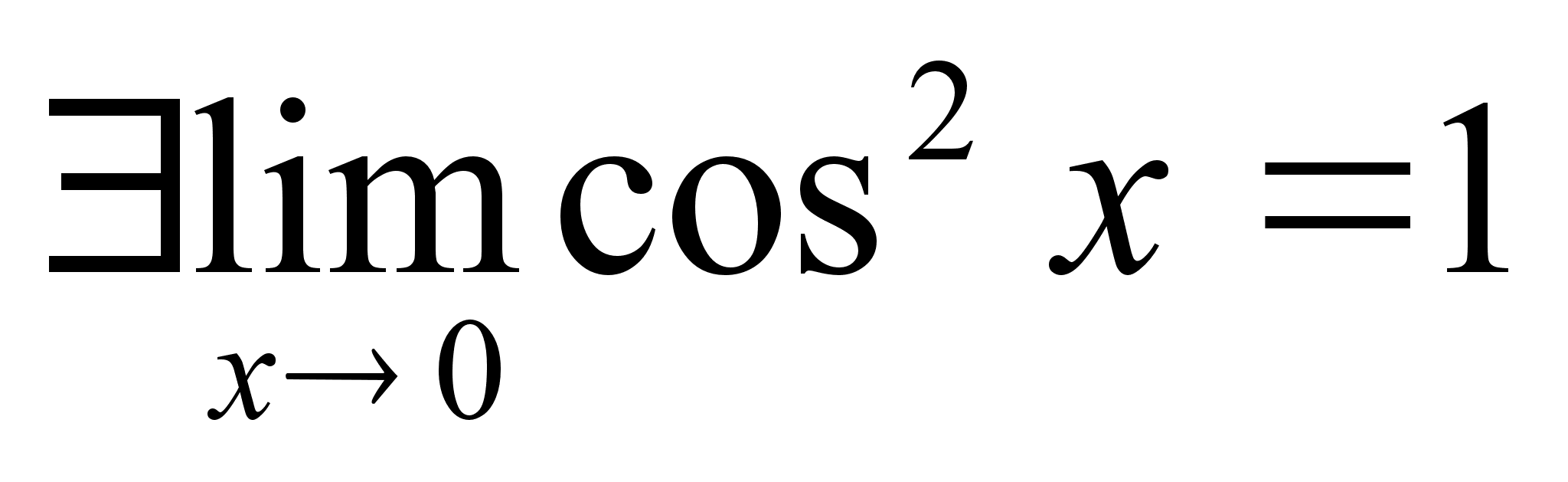
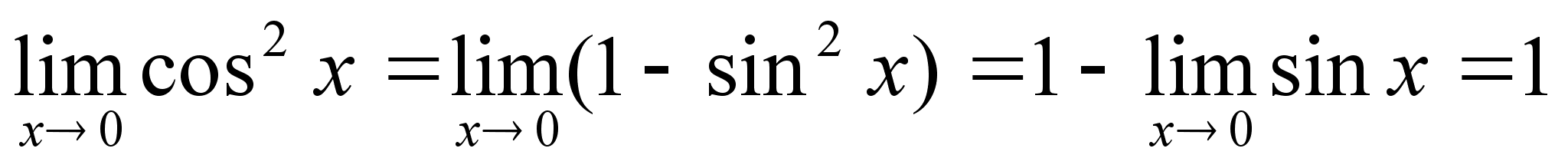
Последнее утверждение:

Второй замечательный предел
Понятие касательной к прямой.
П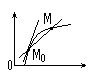 рямая,
проходящая
через две точки
кривой – секущая.
рямая,
проходящая
через две точки
кривой – секущая.
Предельное положение секущей, которое она занимает при стремлении т. М к т. М0 называется касательной к кривой в т. М0
Бесконечные пределы ф-ии.
Если в общем определении предела через окрестности положить в качестве А бесконечно удаленную точку, то получим определение бесконечного предела.
Так как различают три вида бесконечно удаленных точек, то существуют три определения:
1.
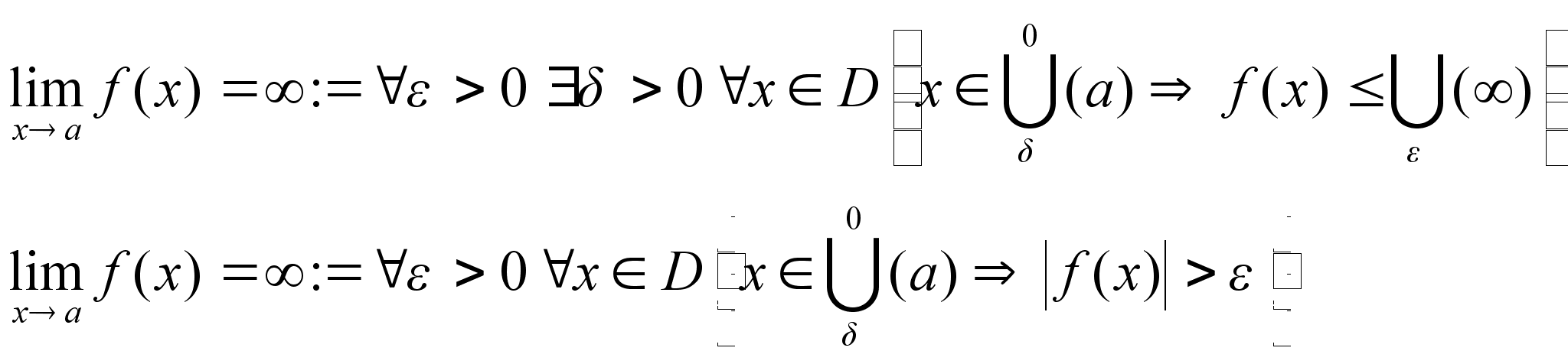
2.

3.
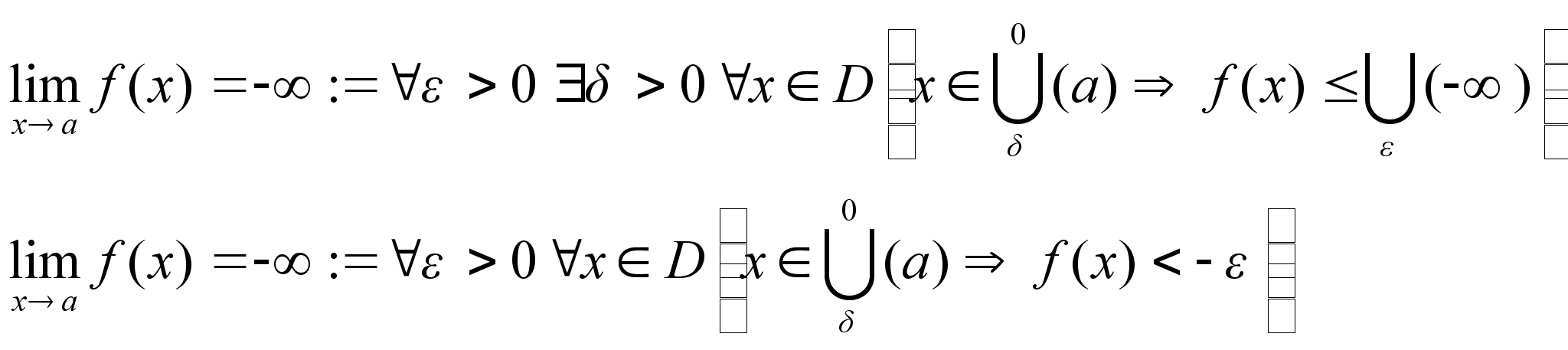
Понятие непрерывности ф-ии.
Непрерывность – такое свойство ф-ии, как отсутствие точек разрыва у графиков этой ф-ии. Т.е. строится единственной непрерывной линией.
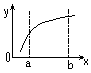
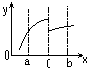
График непрерывной ф-ии ; График ф-ии, разрывной в т. С;
1.Ф-ия
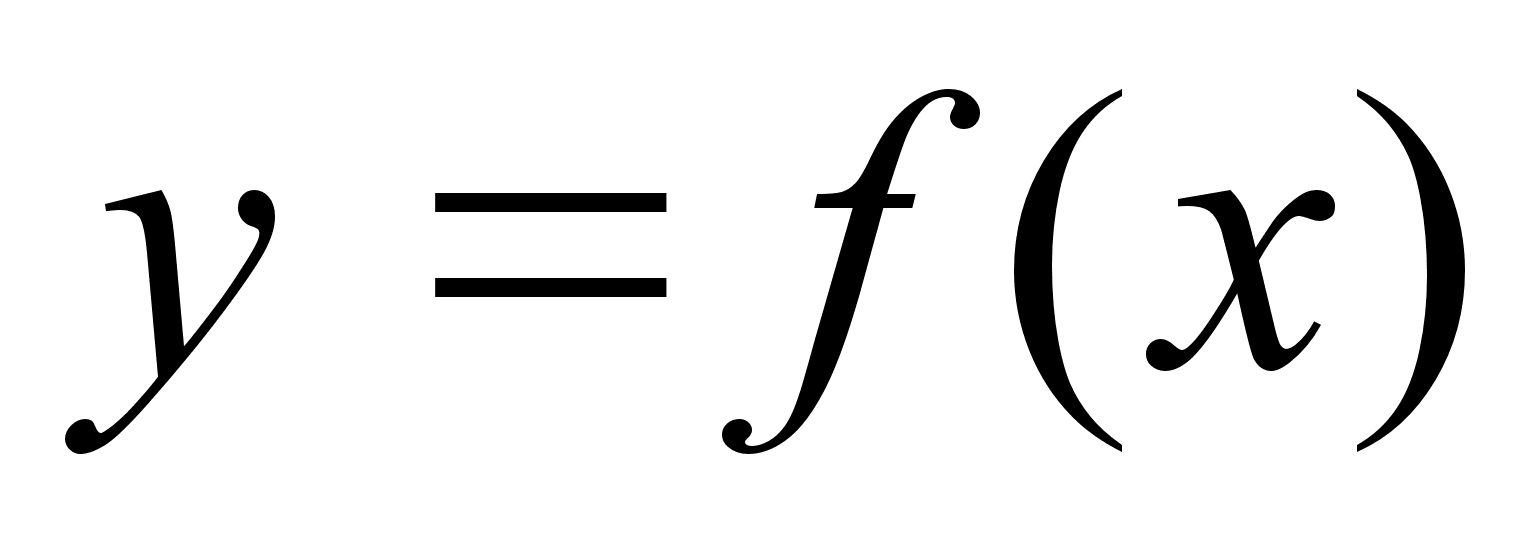 называется
непрерывной
в точке х0
, если предел
называется
непрерывной
в точке х0
, если предел
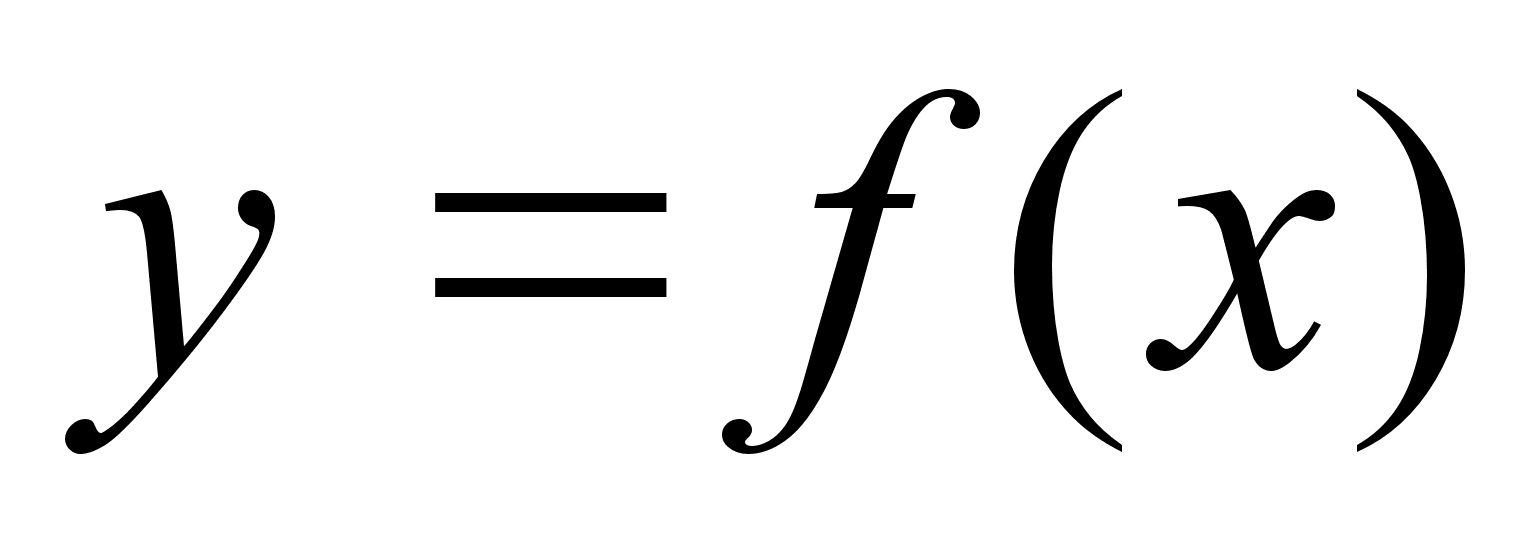 в
данной точке
совпадает со
значением ф-ии
в этой же точке
в
данной точке
совпадает со
значением ф-ии
в этой же точке

2.
3. Разность
 -приращение
аргумента в
точке х0
-приращение
аргумента в
точке х0
4. Разность
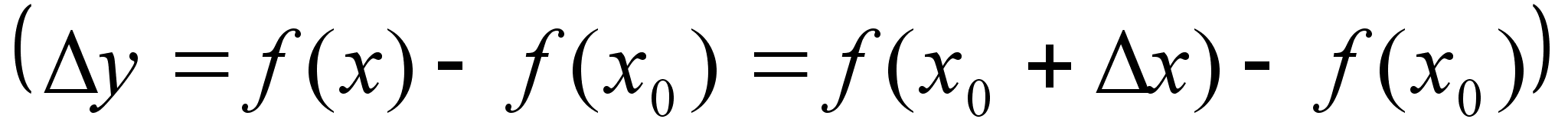 -
приращение
ф-ии в точке х0
вызывает приращение
аргумента
-
приращение
ф-ии в точке х0
вызывает приращение
аргумента
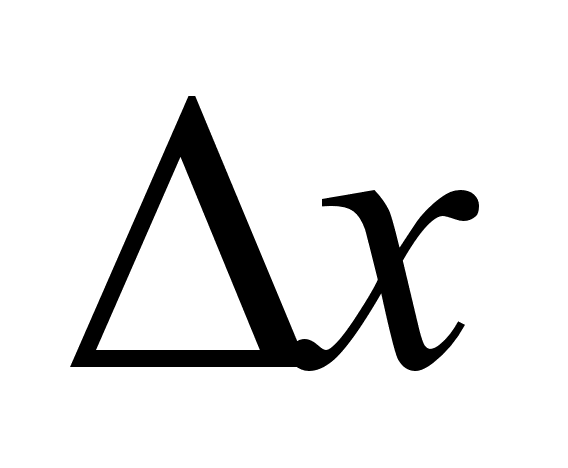
5. Ф-ия
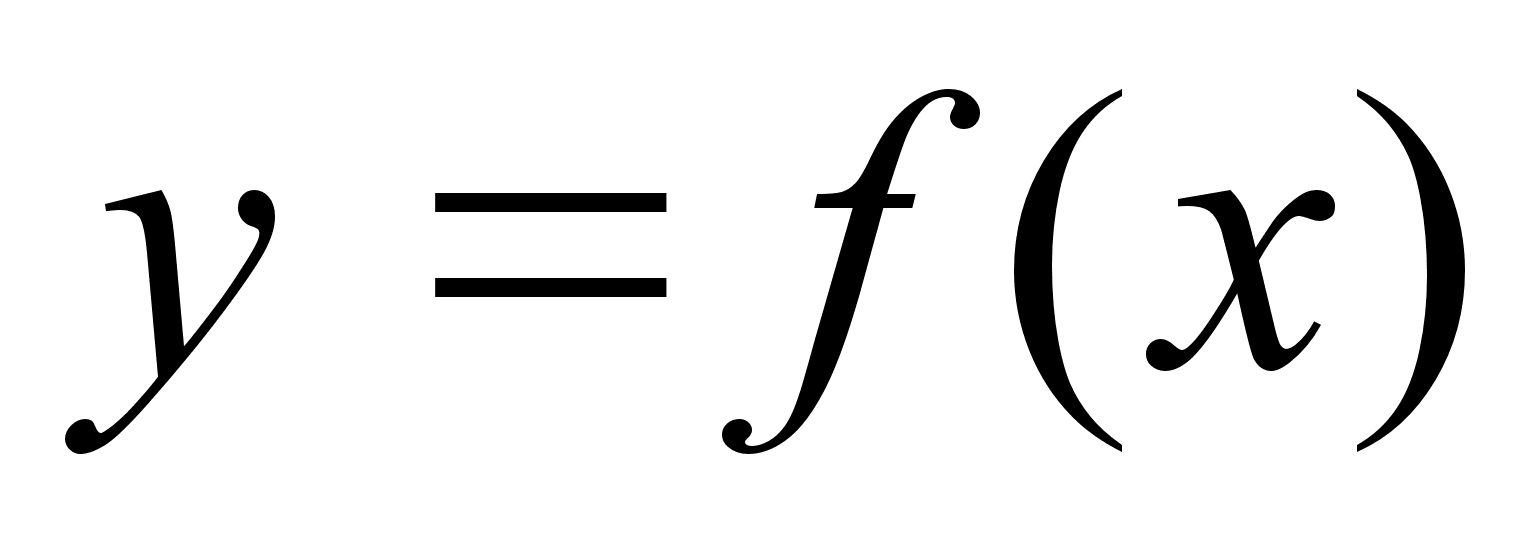 называется
непрерывной
в точке х0
, если бесконечно
малому аргументу
соответствует
бесконечно
малое значение
ф-ии в точке х0
.
называется
непрерывной
в точке х0
, если бесконечно
малому аргументу
соответствует
бесконечно
малое значение
ф-ии в точке х0
.
Общие свойства ф-ии, непрерывной в точке.
Представим ф-ию с помощью бесконечно малых
1.
2.Пусть
ф-ия
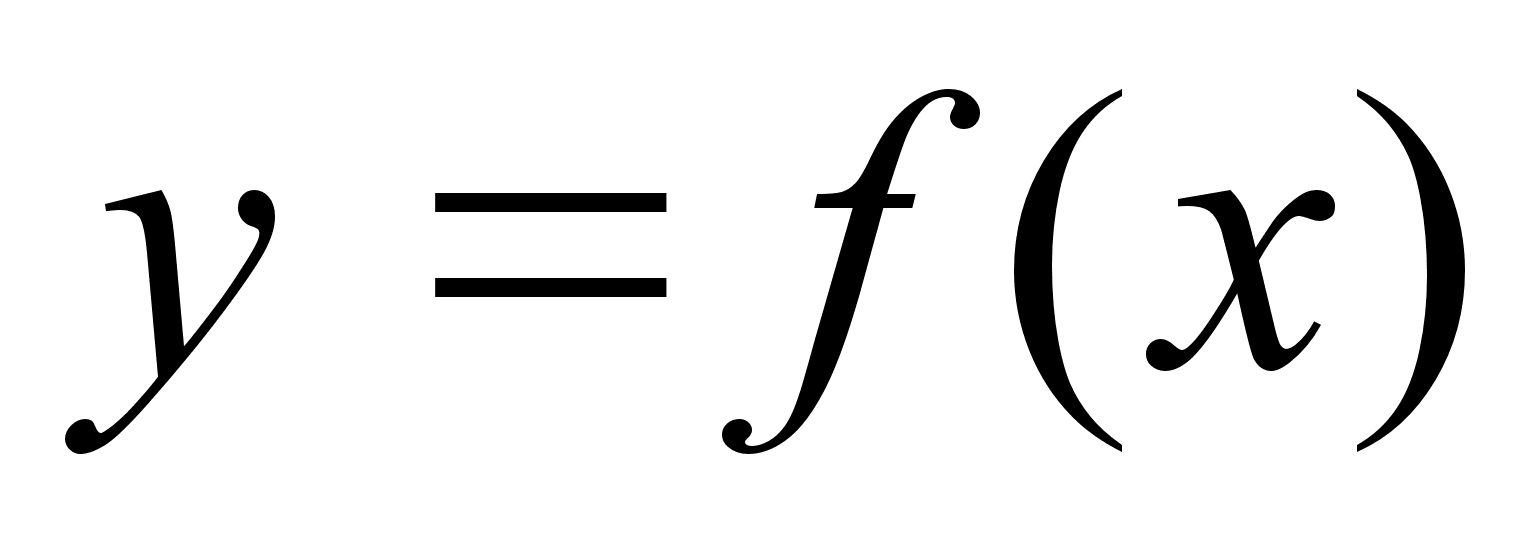 непрерывна
в точке х0
и ее значение
в этой точке
отлично от
нуля, то существует
целая окрестность
х0 , в которой
ф-ия не равна
нулю и сохраняет
знак f(x0)
непрерывна
в точке х0
и ее значение
в этой точке
отлично от
нуля, то существует
целая окрестность
х0 , в которой
ф-ия не равна
нулю и сохраняет
знак f(x0)

sign(х)(сигнум)
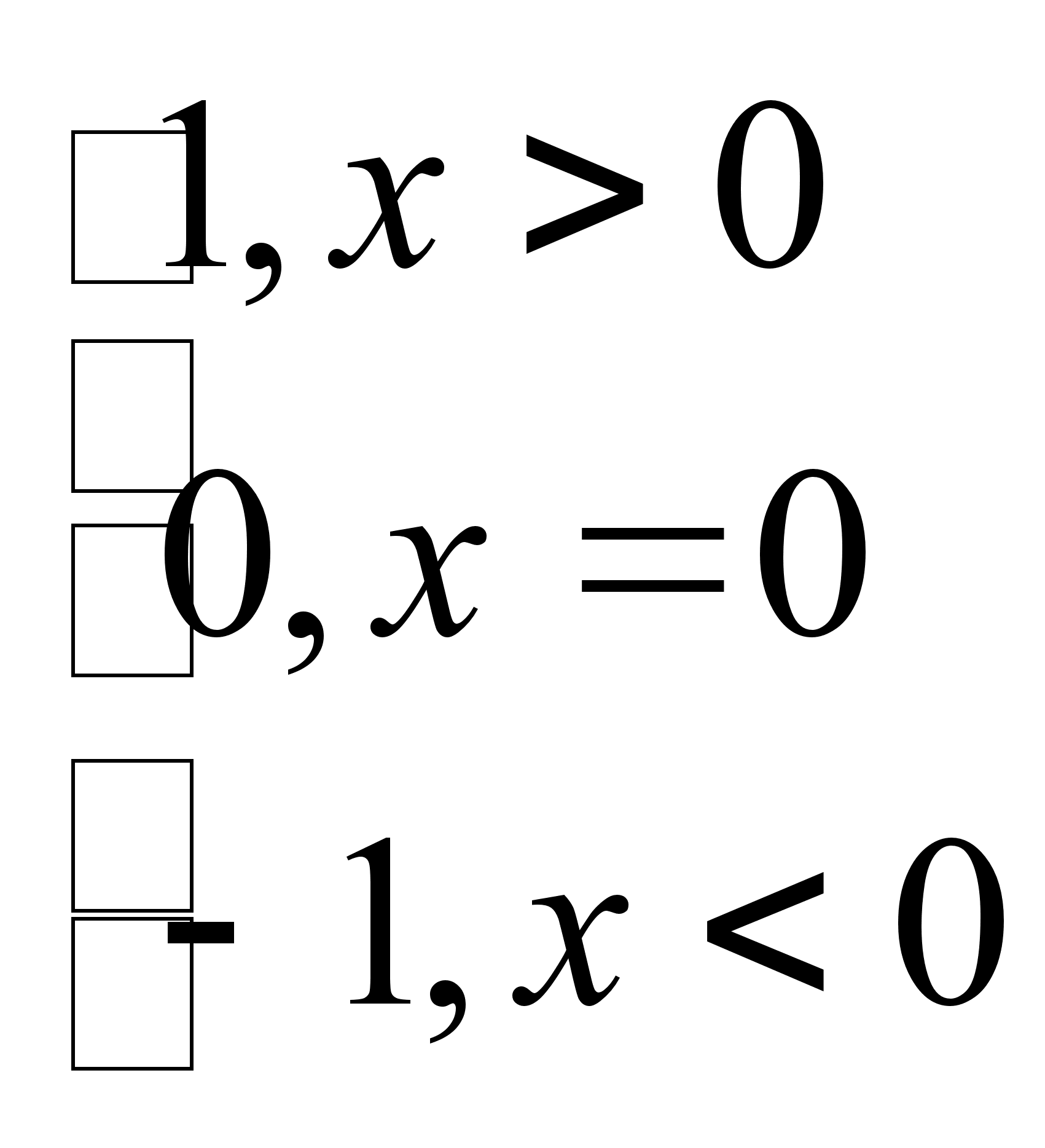
Доказательство:
а)

б)

Из а) и б) следует:

Непрерывность и арифметические операции
Пусть
 и
и
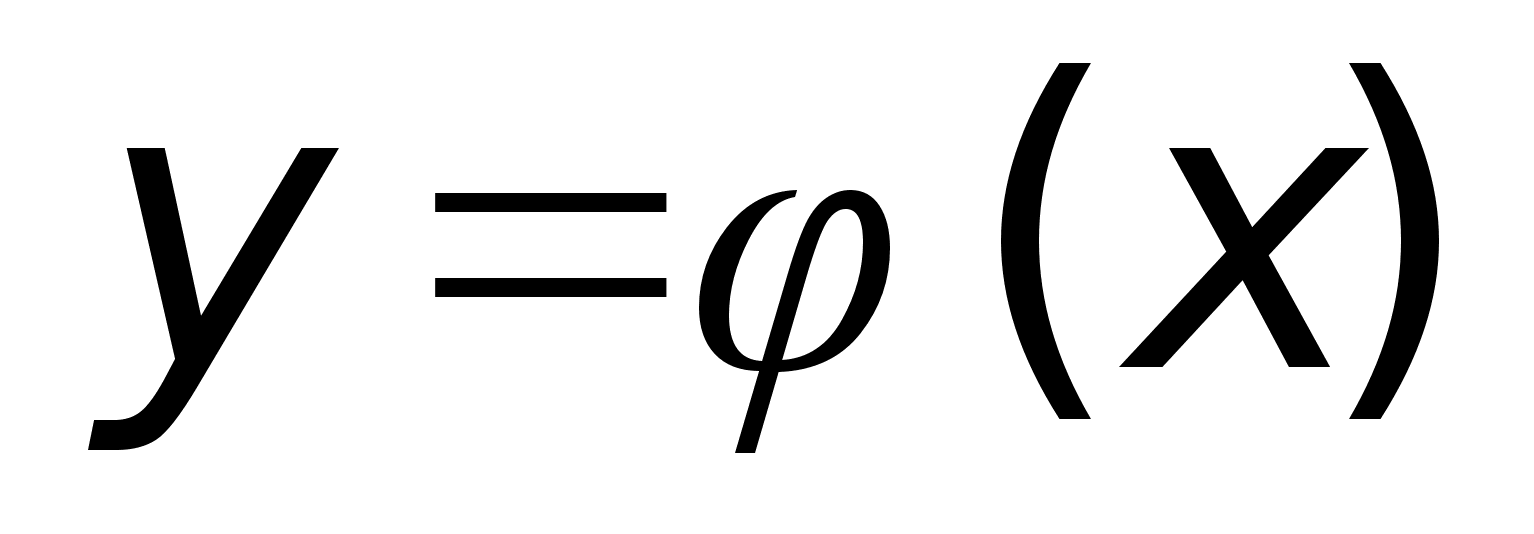 непрерывна
в т. х0
, тогда справедливо:
непрерывна
в т. х0
, тогда справедливо:
Сумма этих ф-ий непрерывна в т. х0 ;
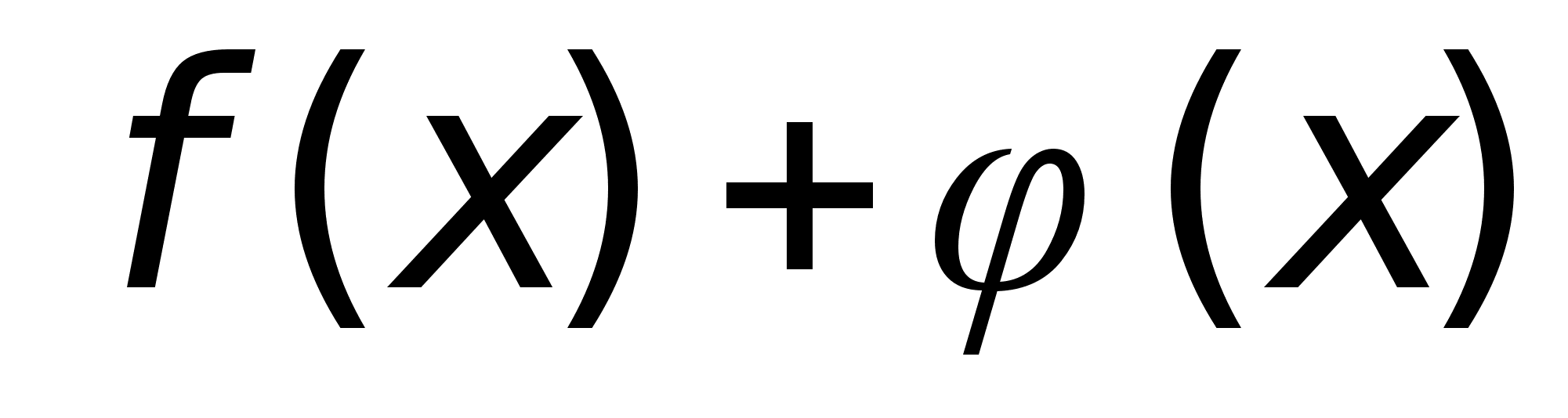 -
непрерывна
в точке х0
-
непрерывна
в точке х0
2. Произведение этих ф-ий непрерывно в т. х0
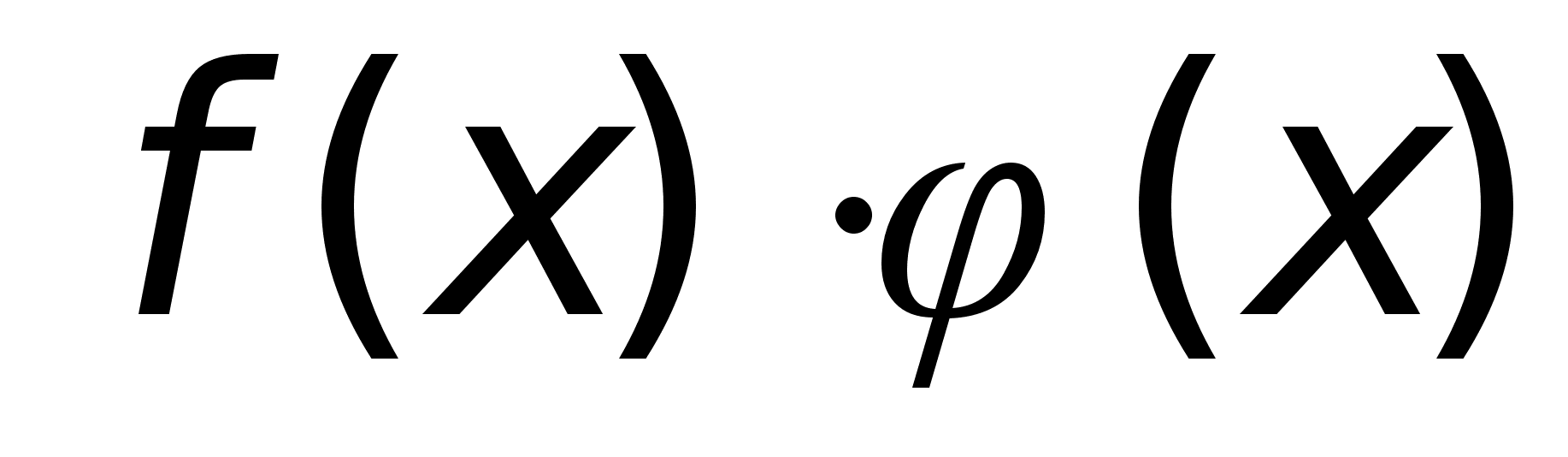 -
непрерывна
в точке х0
-
непрерывна
в точке х0
3. Отношение этих функций непрерывно в тех точках, в которых знаменатель отличен от нуля, т.е. если знаменатель 0.
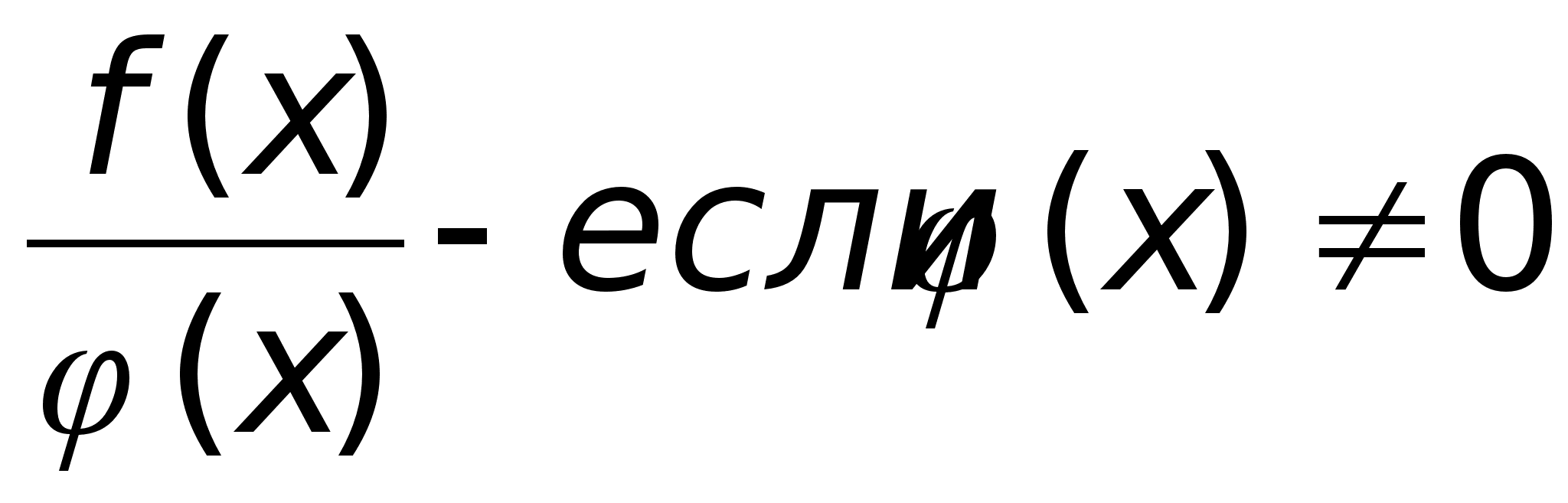
Доказательство:
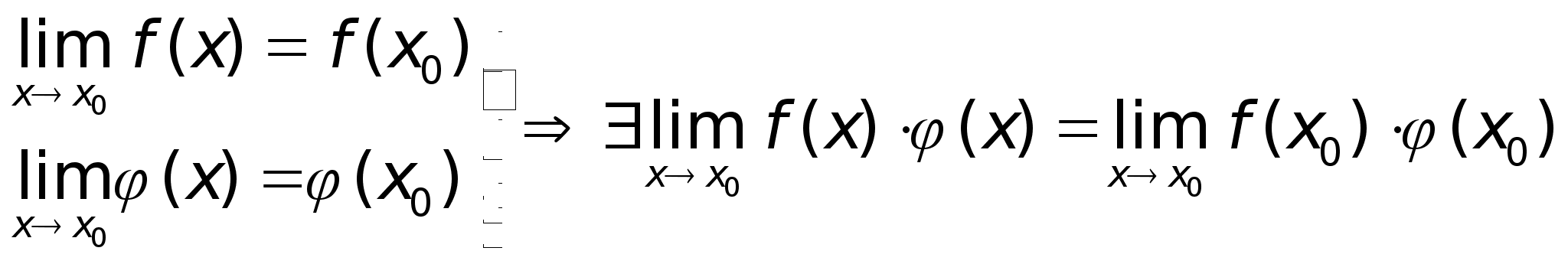
Непрерывность сложной ф-ии.
Пусть:
|
тогда
сложная ф-ия
|
Доказательство:
А).
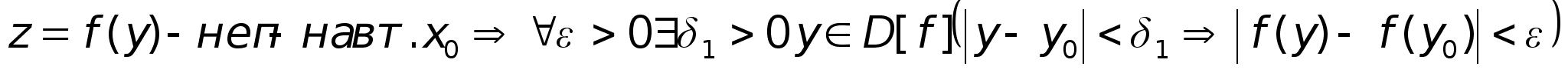
Б).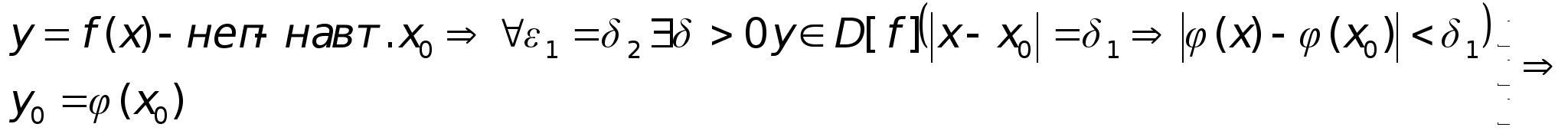
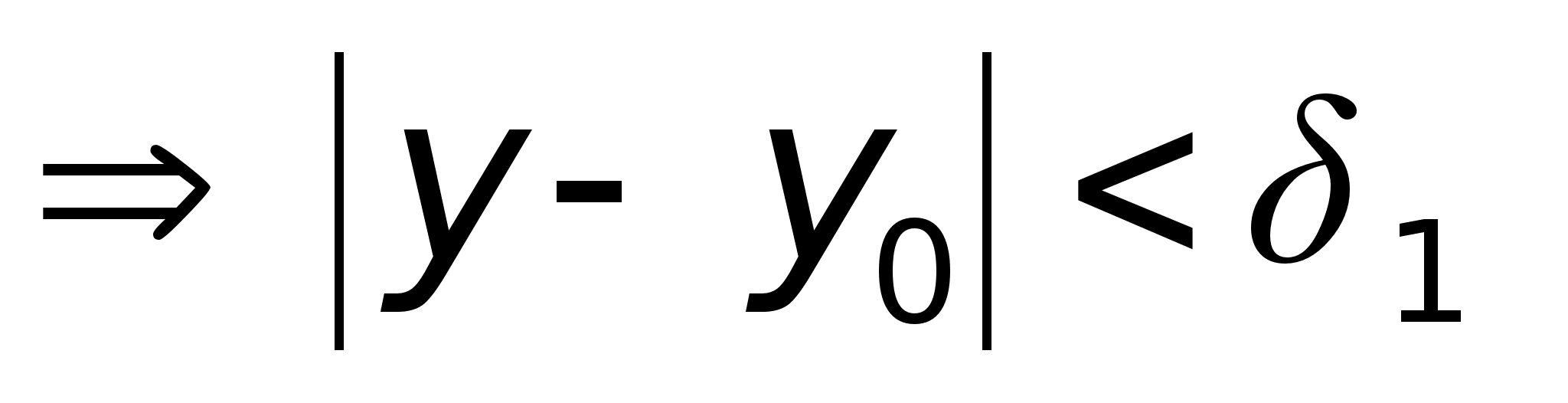
из А) и Б) следует:

Sl.
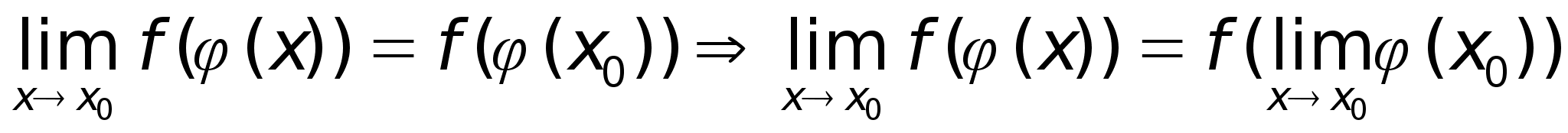
Непрерывность ф-ии на множестве.
Df. Ф-ия непрерывна на множестве Х , если она непрервна в каждой точке этого меожества.
Непрерывность обратной ф-ии:
Пусть
 -
непрерывна
и строго монотонна
на промежуте
Х , тогда
справедливо:
-
непрерывна
и строго монотонна
на промежуте
Х , тогда
справедливо:
*****
На промежутке Y существует непрерыная обратная ф-ия
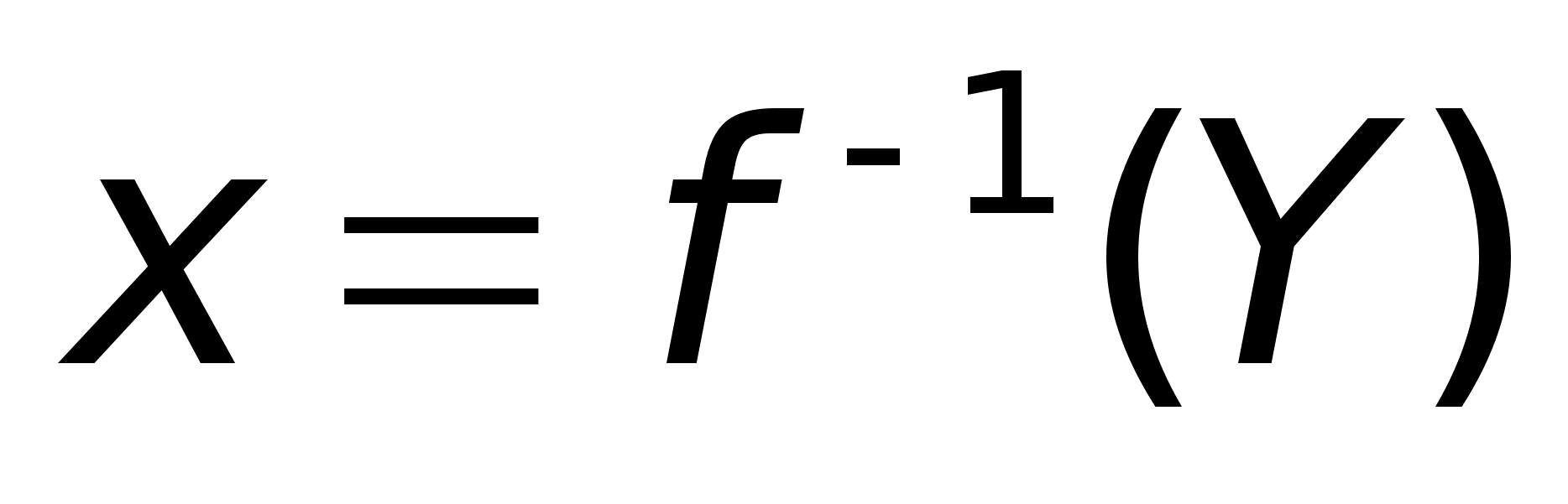 .
.Характер монотонности обратной ф-ии такой же как и прямой.
Непрерывность элементарной ф-ии:
**********
Доказательство непрерывности основной элементарной ф-ии tg и ctg , следует из свойств непрерыности элементарных ф-ий.
Непрерывность log, arcsin, arccos, arstg следует из определения непрерывности обратной ф-ии.
Df Элементарные ф-ии, полученные из основных элементарных ф-ий с помощью арифметических операций, взятых в конечном числе,********
Характеристика точек разрыва ф-ии.
1. Точка устранимого разрыва.
D(f)
т. х0
называется
точкой устранимого
разрыва ф-ии
 ,
если она не
определена
в этой точке,
но имеет конечный
предел.
,
если она не
определена
в этой точке,
но имеет конечный
предел.
Ф-ию можно сделать непрерывной в этой точке, доопределив ей значение в этой точке равным пределом.

2. Точка разрыва первого рода.
D(f) х0 – точка разрыва первого рода, если существует конечный левосторонний и правосторонний предел не равные между собой.
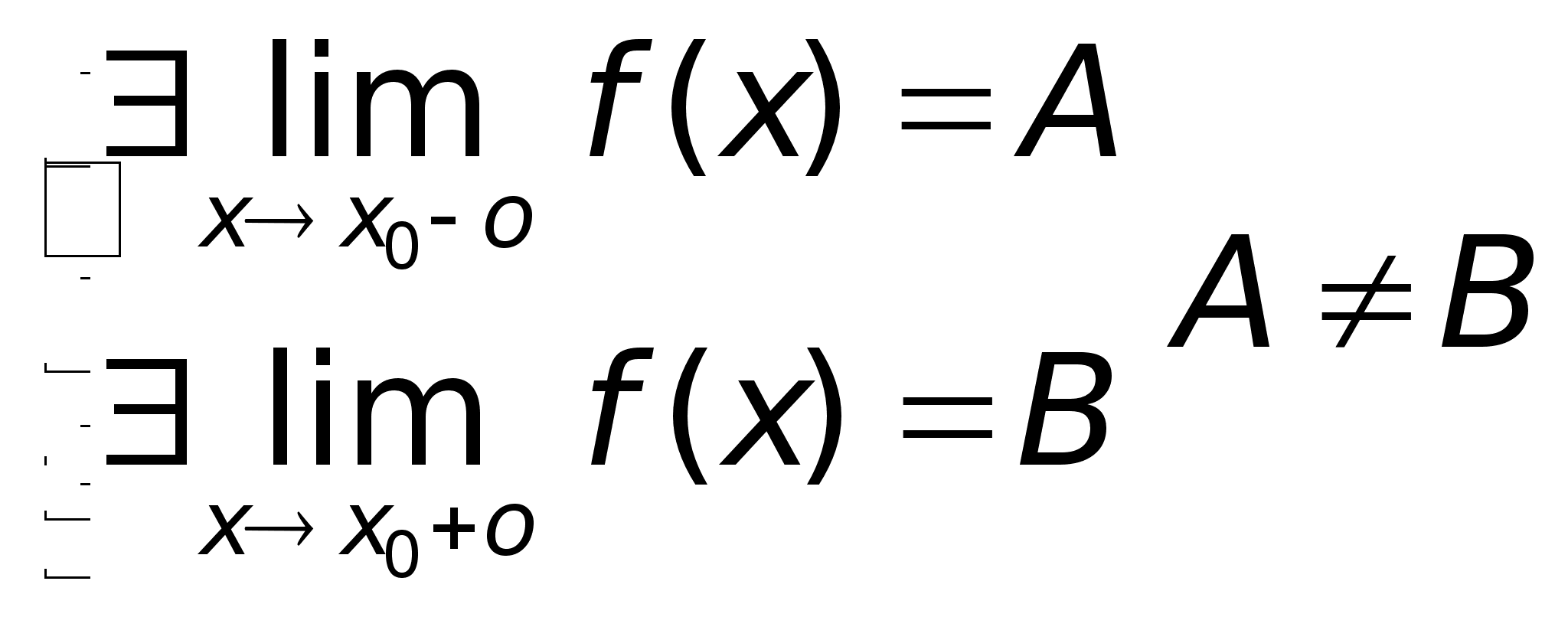
Разницу (b-a)называют скачком ф-ии в т. х0
3. Точка разрыва второго рода.
*********************************
Односторонняя непрерывность ф-ии.
Если в D(f)1 непрерывности предел заменить односторонним пределом, то получим определение односторонней непрерывности ф-ии.
Ф-ия называется непрерывной в точке х0 справа, если правосторонний предел совпадает со значением ф-ии.
Ф-ия называется непрерывной в точке х0 слева, есди левосторонний предел совпадает со значением ф-ии.
Например:
 -
исследуем
предел ф-ии
справа и слева:
-
исследуем
предел ф-ии
справа и слева:
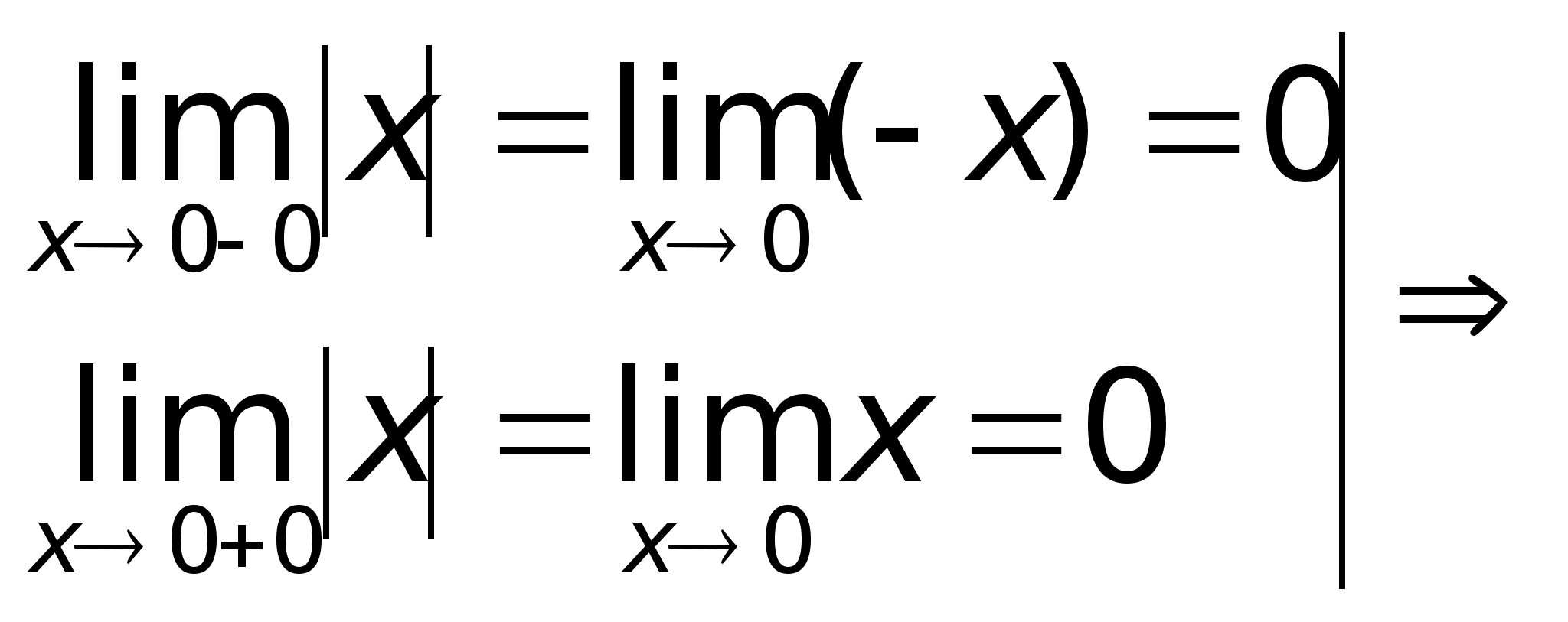 ф-ия
непрепывна
в точке х=0.
ф-ия
непрепывна
в точке х=0.
Для непрерывности в точке х0 необходимо и достаточно, чтобы она была непрерывна слева и справа в этой точке.
Свойства ф-й, непрерывных на отрезке
Ф-ия называется непрерывной на отрезке [a,b], если она непрерывна на интервале(a,b) и в т. а непрерывна справа а в т. b – слева.
Т1:
Ф-ия
 ,
непрерывная
на [a,b],
ограничена
на этом отрезке.
,
непрерывная
на [a,b],
ограничена
на этом отрезке.
 -
непрерывная
на [a,b]
-
непрерывная
на [a,b]

D(f)
: число М
называется
наибольшим
значением ф-ии
на отрезке
[a,b],
если существует
такое число
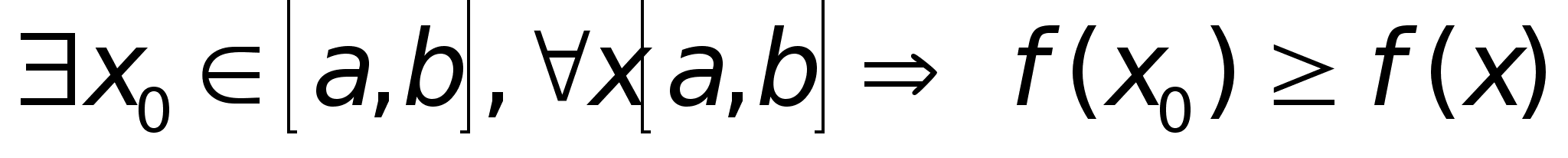 .
.
D(f)
:точка называется
наименьшим
значекнием
ф-ии на [a,b],
если

Т2
: ф-ия
 ,
непрерывная
на [a,b],имеет
на [a,b]
наибольшее
и наименьшее
значения.
,
непрерывная
на [a,b],имеет
на [a,b]
наибольшее
и наименьшее
значения.
Т3 : *************
Sl1 : (f) ф-ии, непрерывной на отрезке, является отрезок
Sl2 (Т3): ф-ия, непрерывная на отрезке [a,b], имеющая различные по знаку значения, на его границах обязательно обращается в ноль, хотя-бы в одной точке этого отрезка.
*******************************************
Дифференциальное счисление.
Ф-ия одной переменной.
1. Задачи, приводящие к понятию производной.
3.1. Задача о вычислении скорости точки, движущейся вдоль прямой.
Пусть точка движется вдоль прямой х.
****************************************** - l-единичный вектор, задающий направление вдоль прямой.
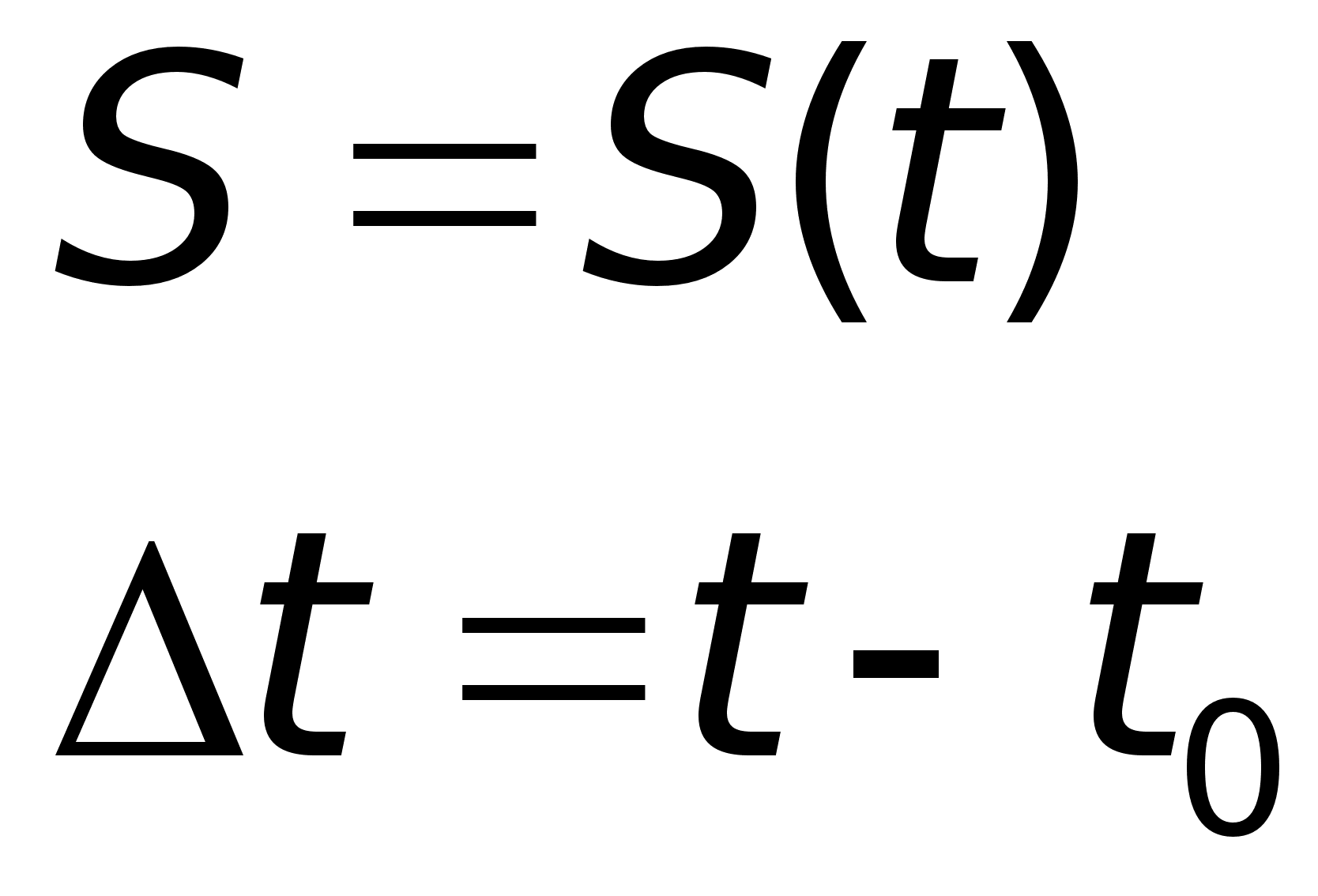

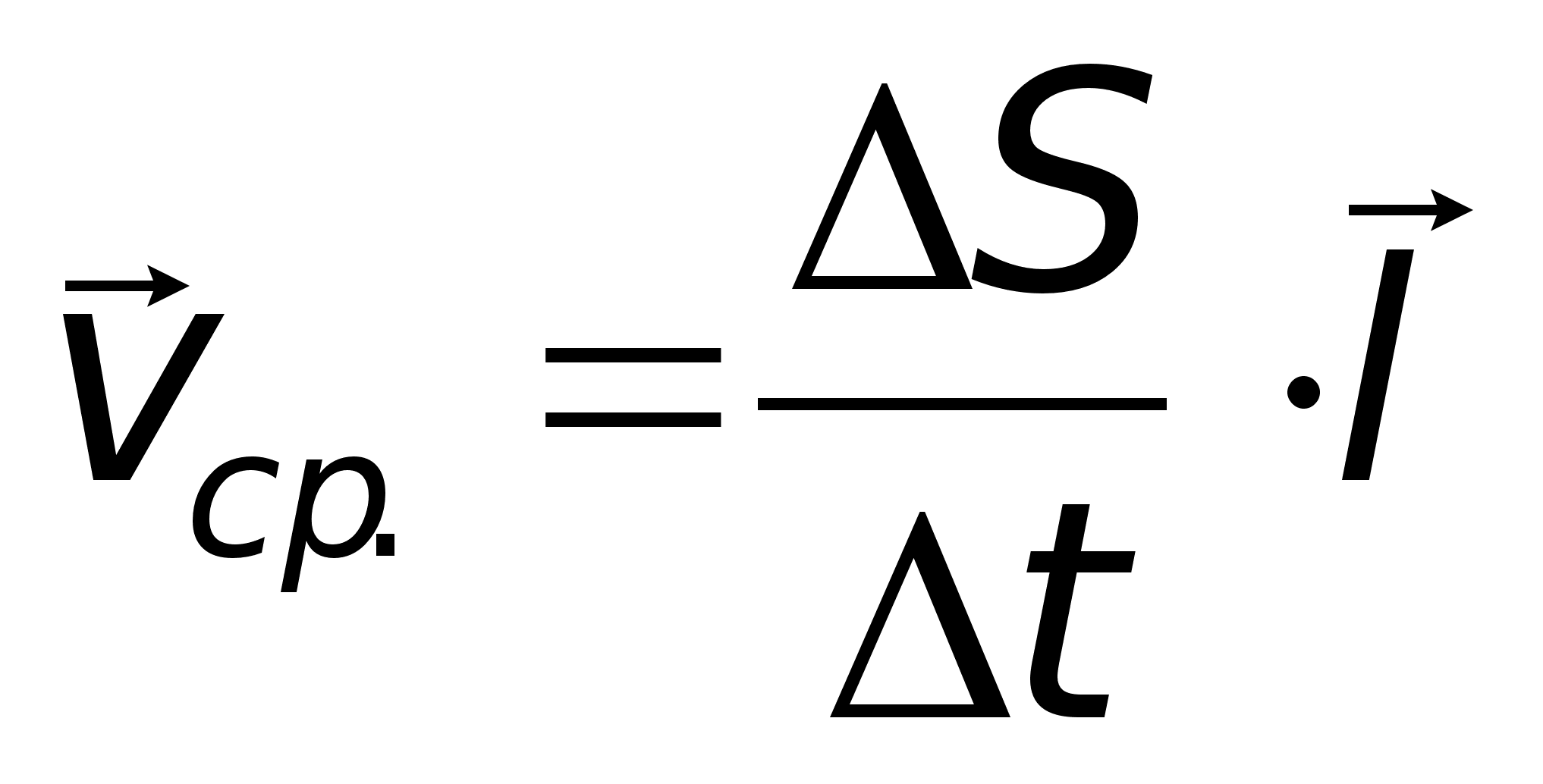

3.2 Построение
касательной
к кривой с уравнением
 в т. х0
.
в т. х0
.
********************
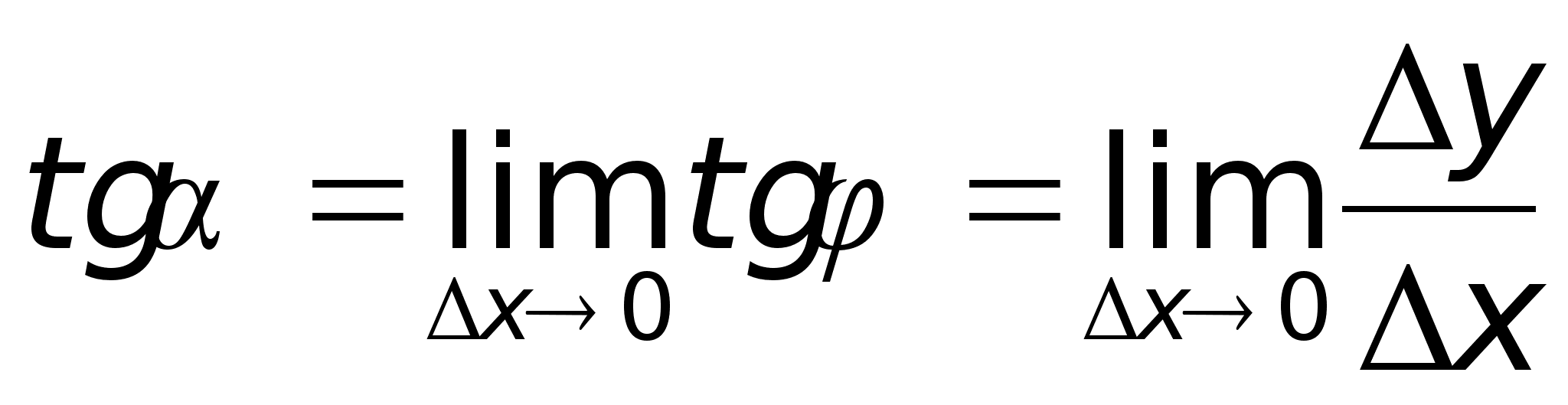
Задачи, различные по смыслу, из разных областей науки, свелись к вычислению одного и того же предела. В таких случаях в математике абстрагируются от крнкретных задач и изучают отдельно предел ф-й.
Определение призводной ф-ии в точке.
Обозначение:
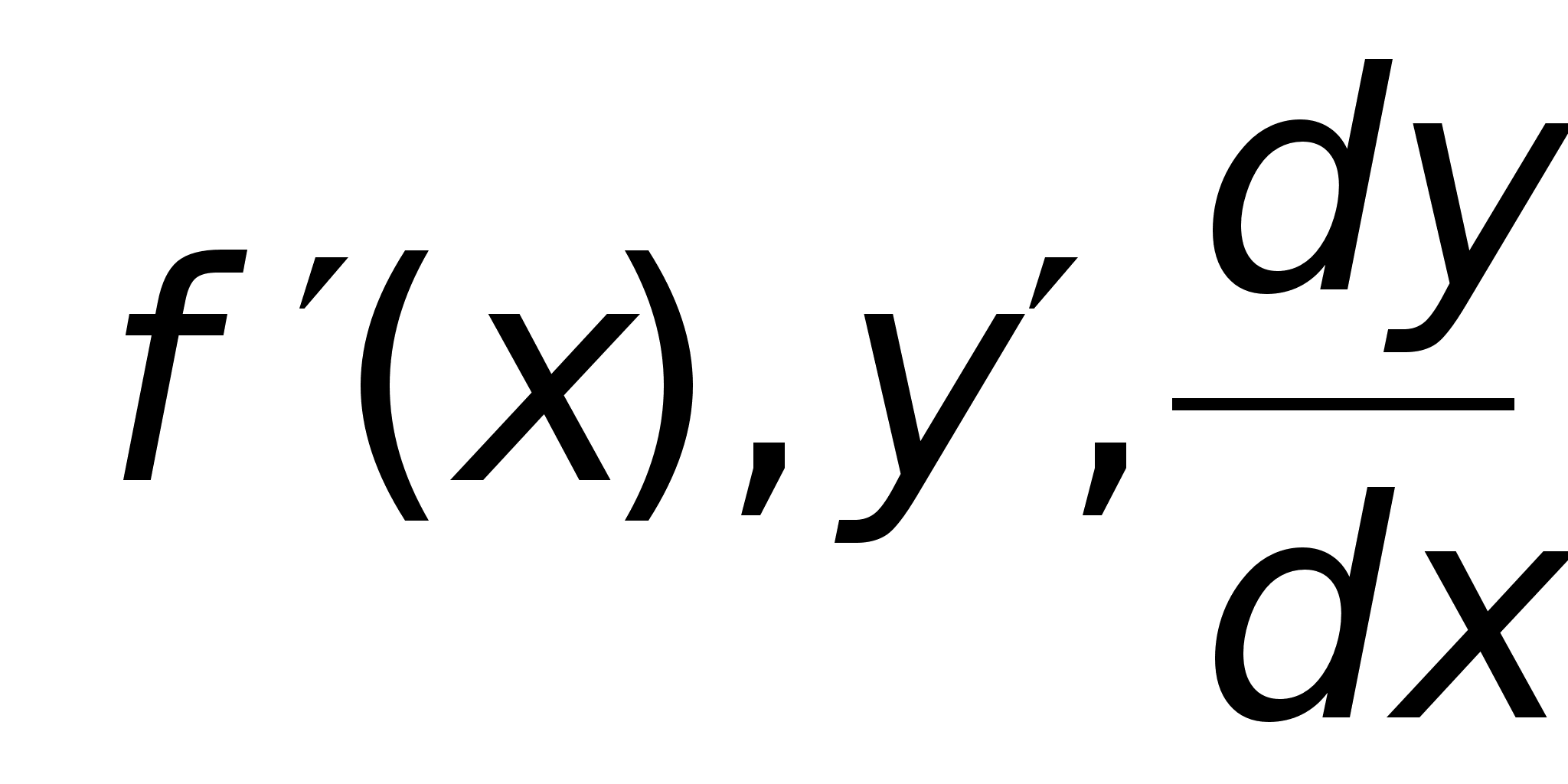
Df1
Производной
ф-ии
 в
т. х
называют предел
отношения
приращения
ф-ии в этой т.
к приращению
аргумента, при
стремлении
последнего
к нулю.
в
т. х
называют предел
отношения
приращения
ф-ии в этой т.
к приращению
аргумента, при
стремлении
последнего
к нулю.

Пример:
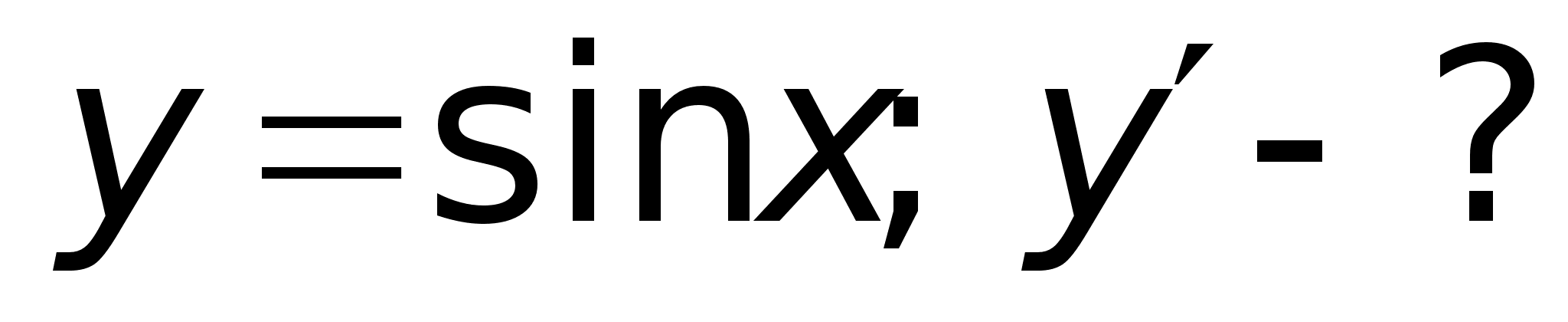
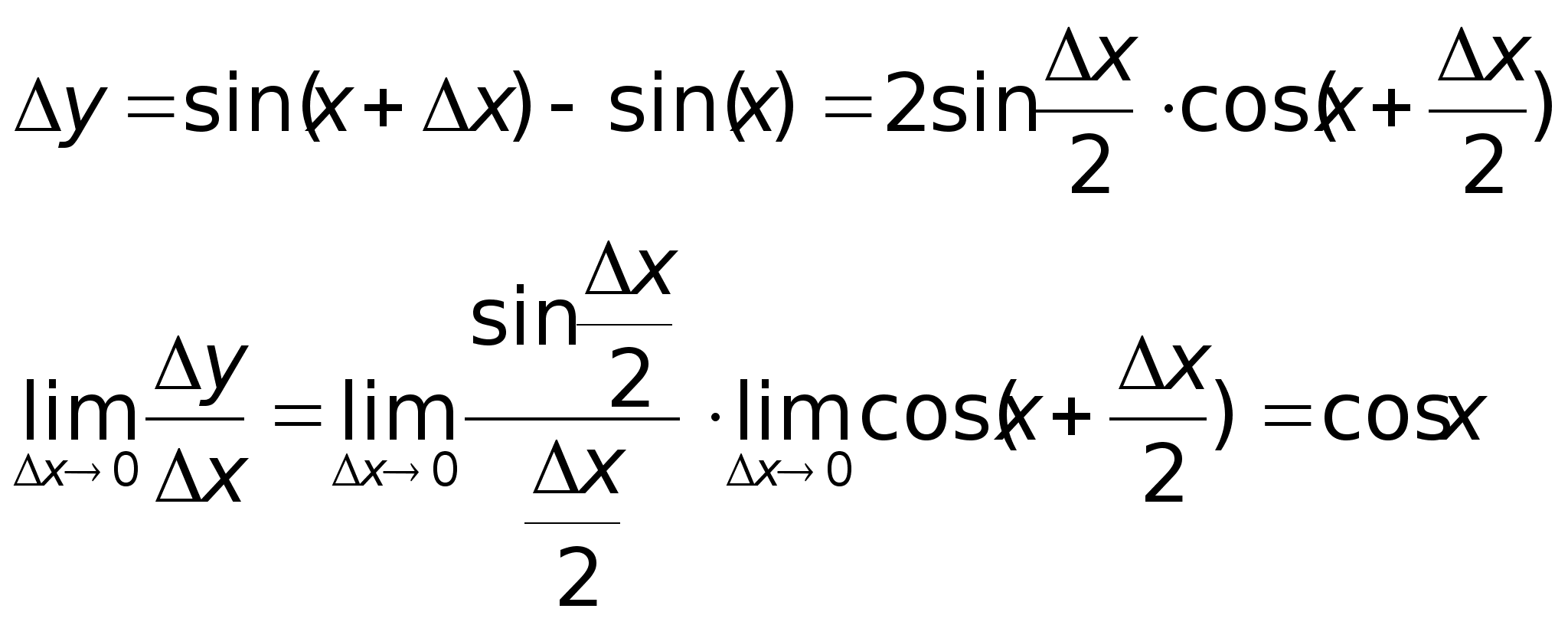
 -
непрерывная.
-
непрерывная.

Степень ф-ии с вещественным показателем.
Справка:
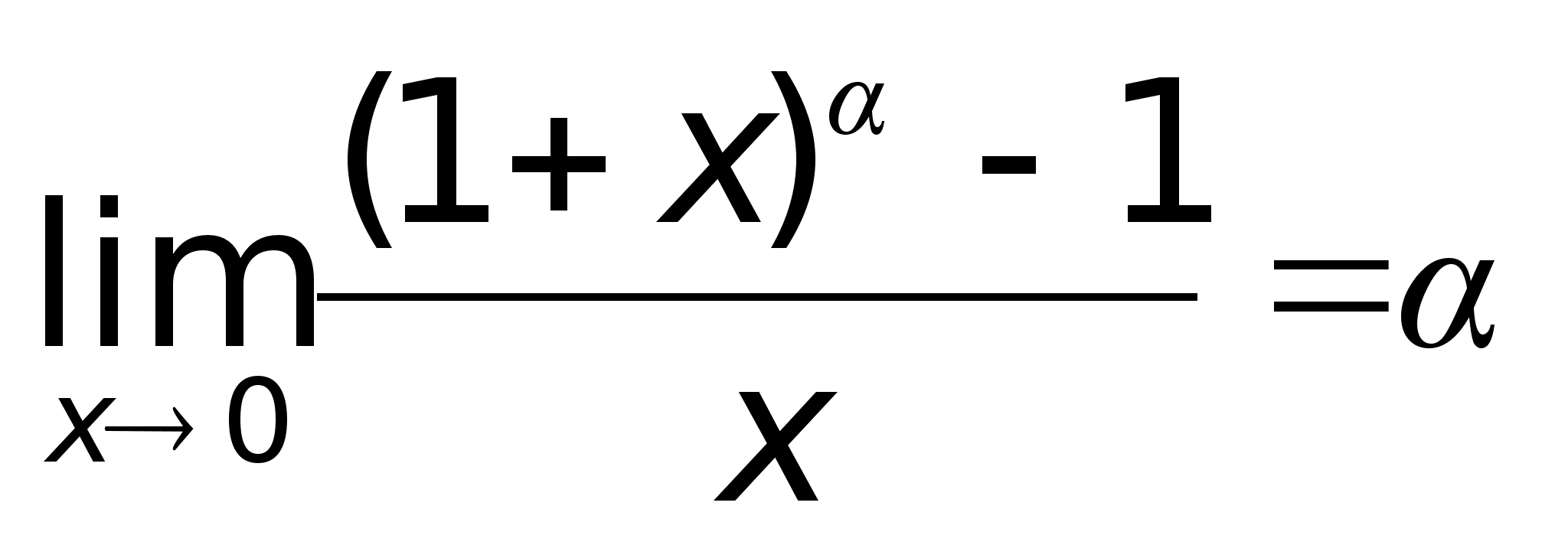 .
.

Геометрический смысл производной.
Из второй
задачи следует,
что поизводная
ф-ии
 в т. х0
=тангенсу угла
наклона касательной,
проведенной
к графику ф-ии
в этой точке.
в т. х0
=тангенсу угла
наклона касательной,
проведенной
к графику ф-ии
в этой точке.
Sl1
: Уравнение
касательной
к кривой. Его
можно написать,
зная точку,
через которую
она проходит,
и угловой коэффициент
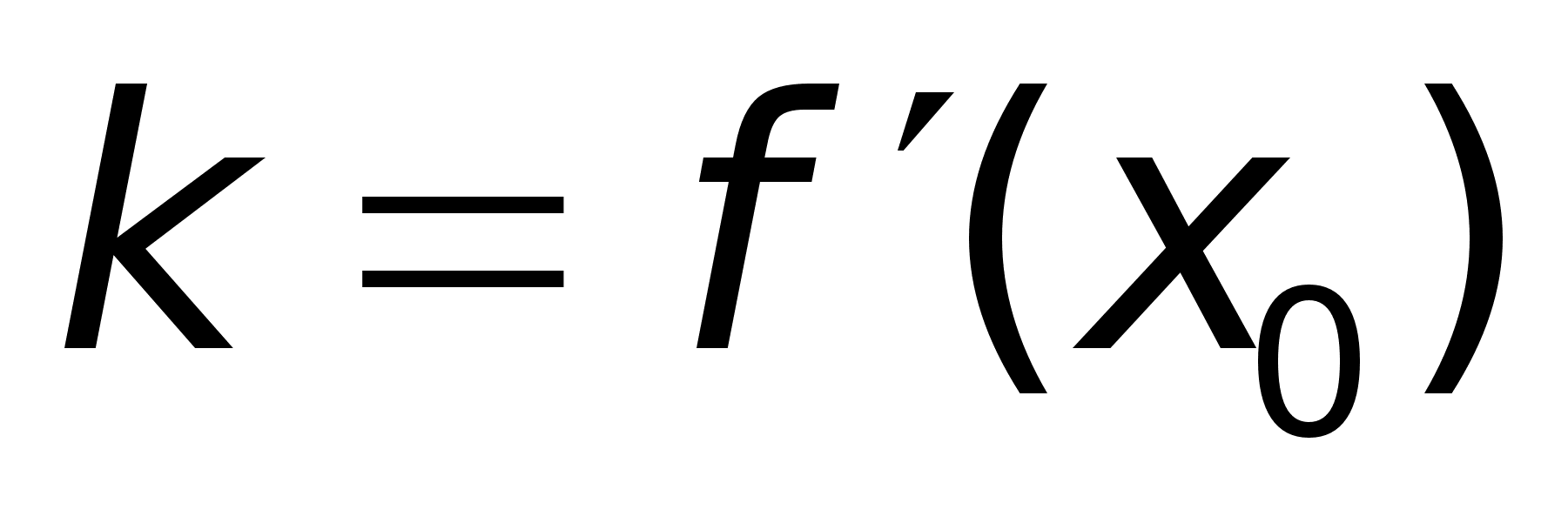
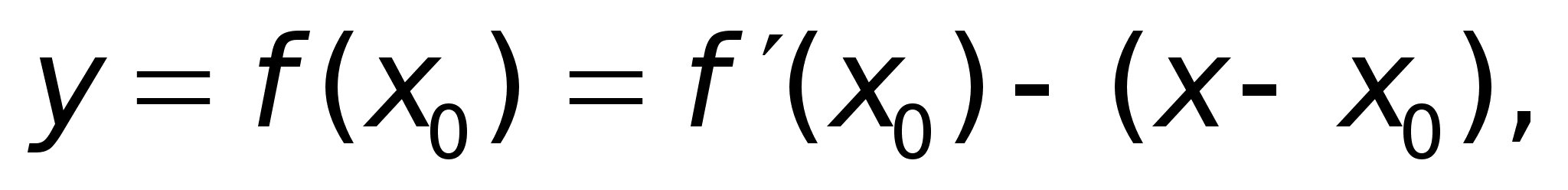 где
x и
y
– координаты
т. на касательной.
где
x и
y
– координаты
т. на касательной.
Sl2
: Уравнение
нормали. Его
можно написать,
зная точку,
через которую
она проходит
и угловой коэффициент

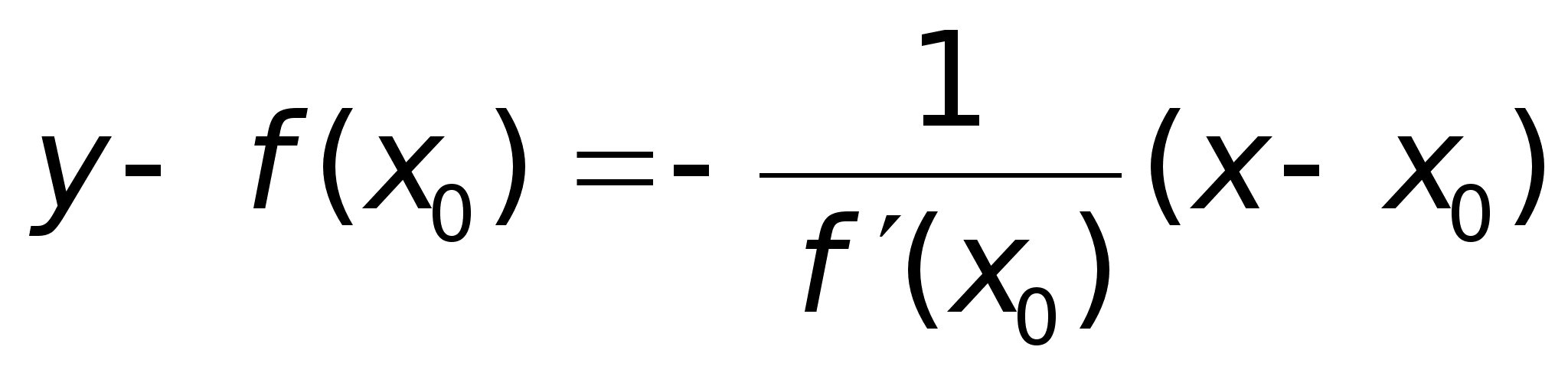 ,
x и
y
– точки на нормали.
,
x и
y
– точки на нормали.
Механический смысл производной.
************
Дифференцируемость ф-ии.
Df
: Ф-ия
 дифференцируема
в точке х0
, если приращение
ф-ии в точке
сможет быть
представлено
в виде:
дифференцируема
в точке х0
, если приращение
ф-ии в точке
сможет быть
представлено
в виде:
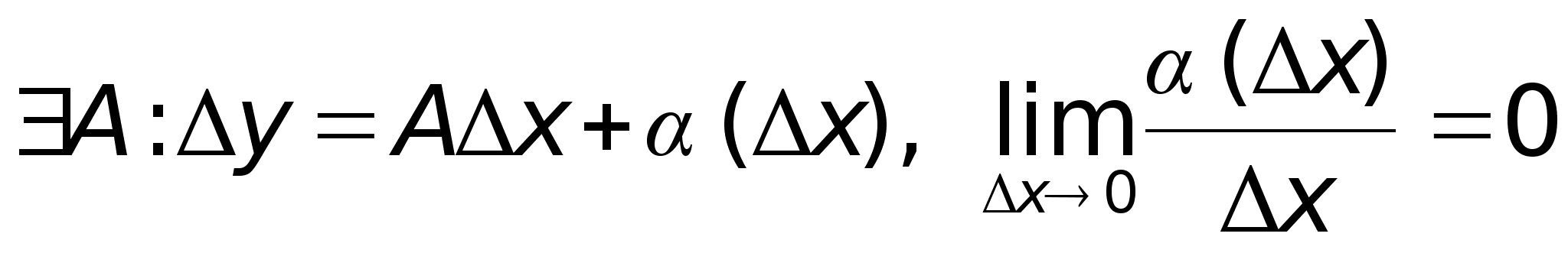 ,
А – const.
,
А – const.
Dh: Для дифференцирования ф-ии в т. х0 , необходимо и достаточно, чтобы в этой точке существовала производная.
Доказательство: (необходимость)

(достаточность):
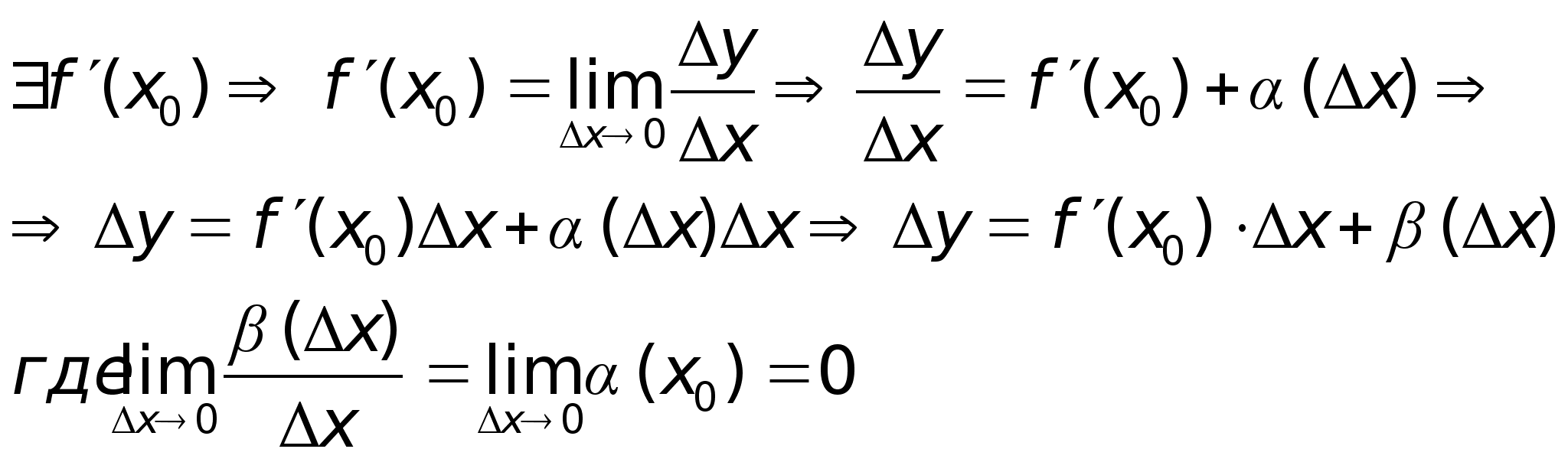
Производная суммы, произведения, частного.
Dh:Пусть
ф-ия
 и
и
 дифференцируемы
в точке х0
, тогда в этой
точке дифференцируемы
их сумма, произведение
и частное, причем
выполняются
формулы:
дифференцируемы
в точке х0
, тогда в этой
точке дифференцируемы
их сумма, произведение
и частное, причем
выполняются
формулы:
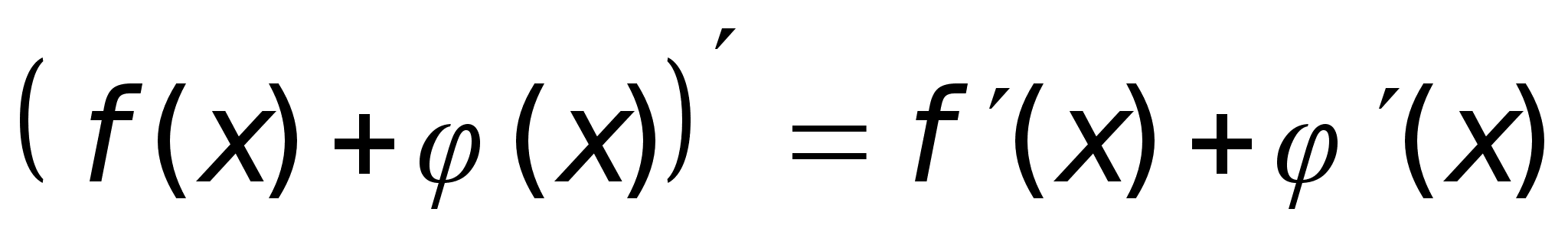
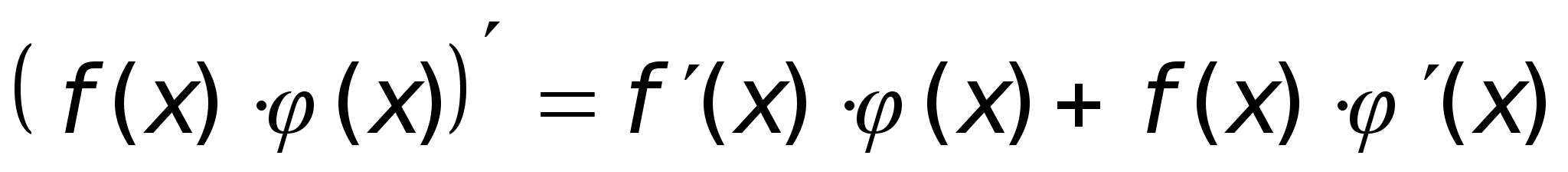
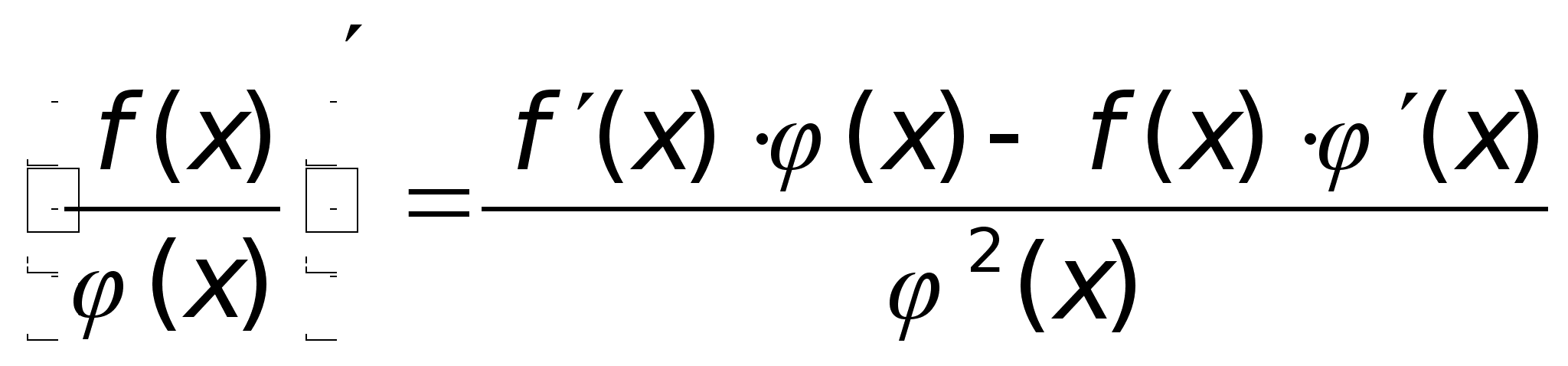 ,
если
,
если
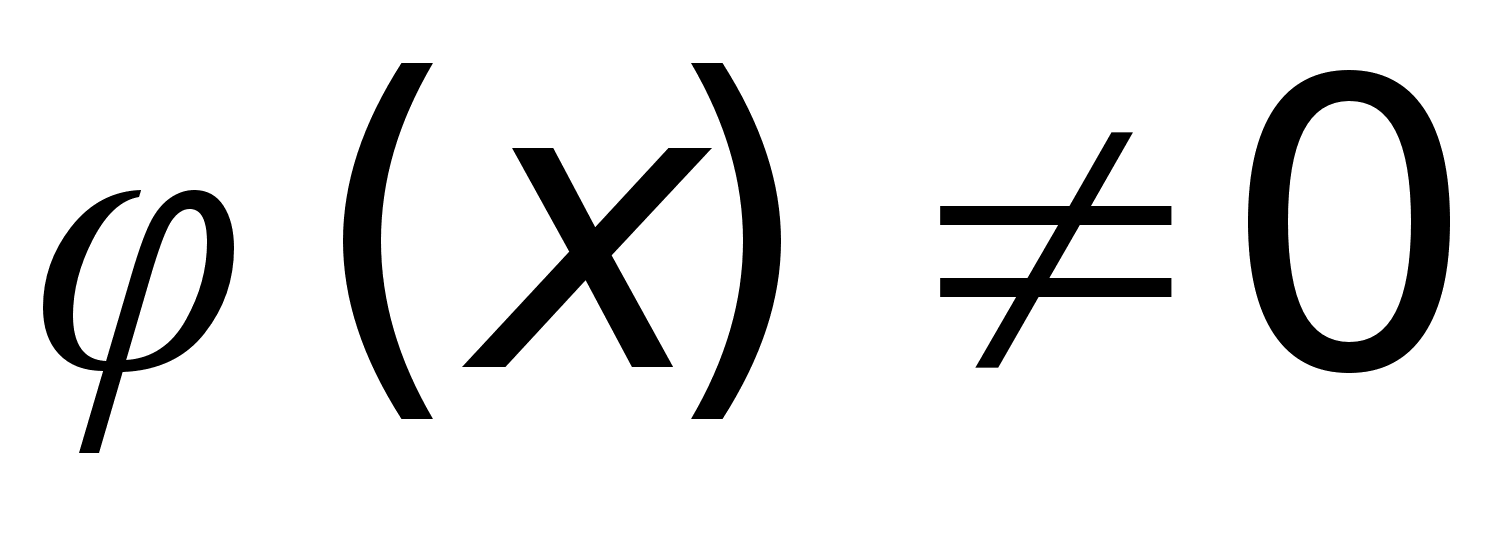
Лемма: Ф-ия, дифференцируема в точке х0 , непрерывнна в этой точке.
 -
дифф. в т. х0
-
дифф. в т. х0
обратное утверждение неверно!!!
Производная от const ф-ии =0.
Если
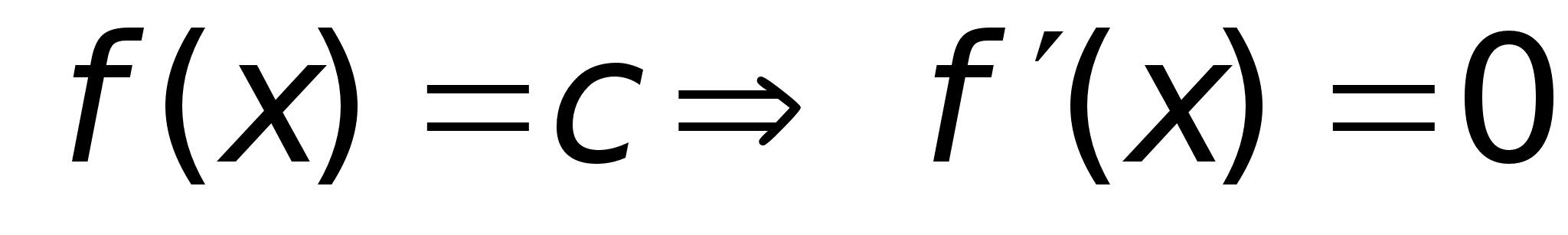
Доказательство:
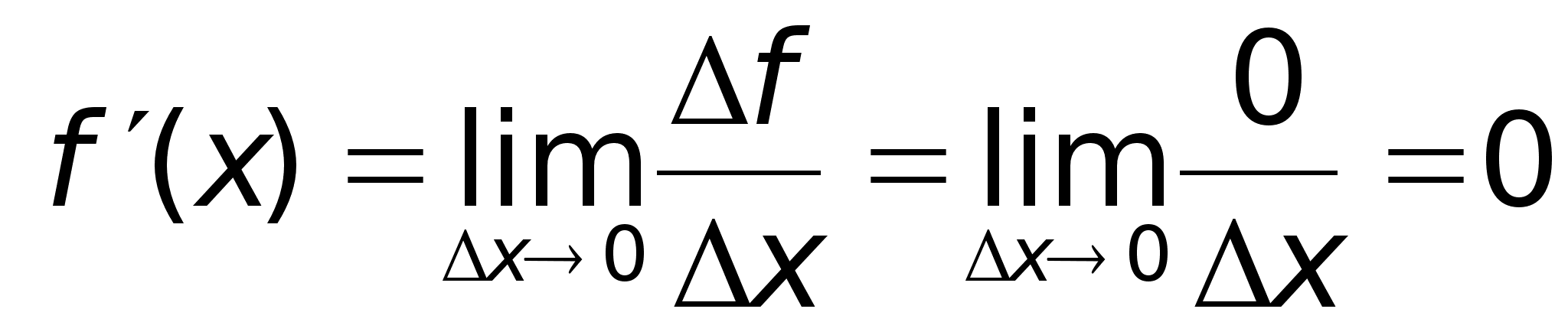
Zm1: При вычислении производной, константу можно выносить за знак производной.
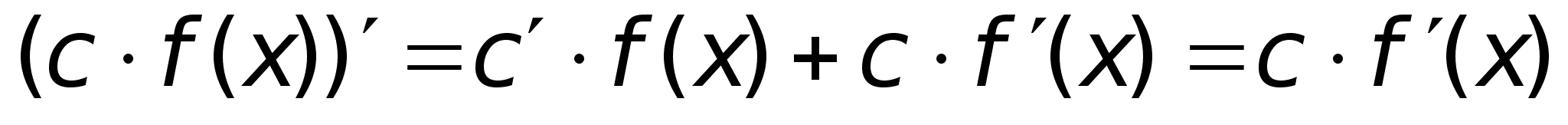
Zm2: Данные формулы можно рассматривать на большее число слагаемых и сомножителей.
Df:
Линейным колебанем
системы из т.
ф-ий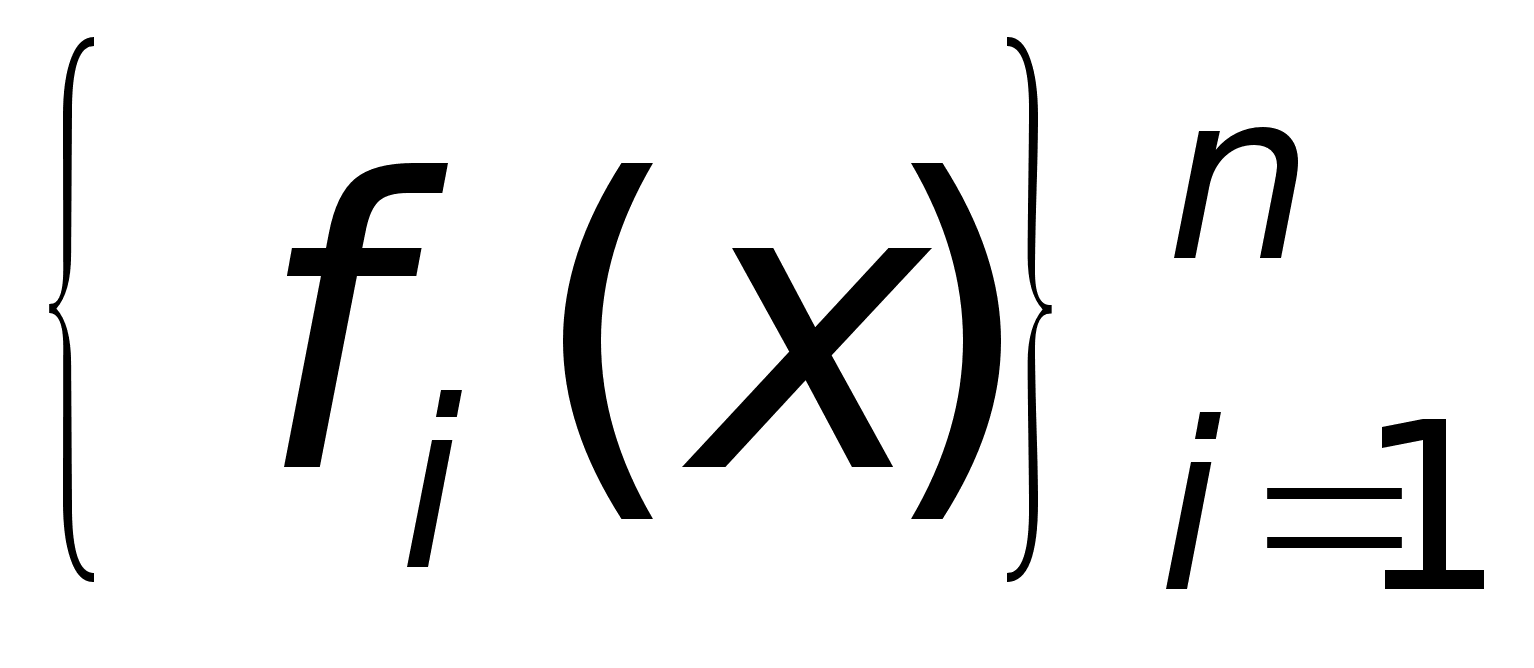 называется
сумма призведения
этих ф-ий на
производную
и постоянную.
называется
сумма призведения
этих ф-ий на
производную
и постоянную.
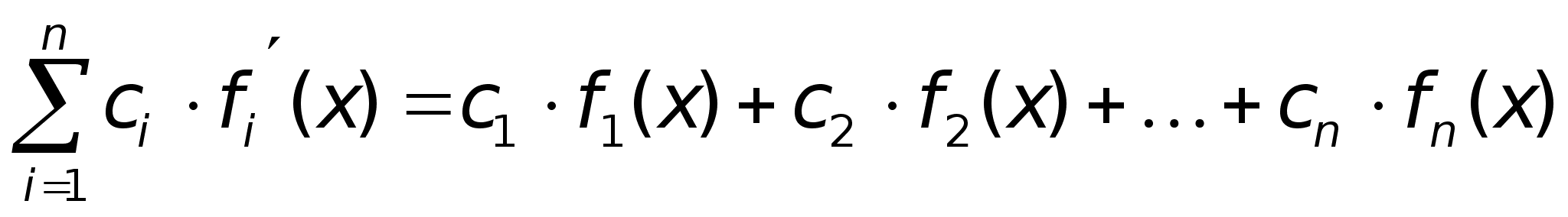
Zm: Свойство линейности производной.
Из доказанных свойств, следует, что производная от линейных колебаний ф-й = линейные комбинации призводных.
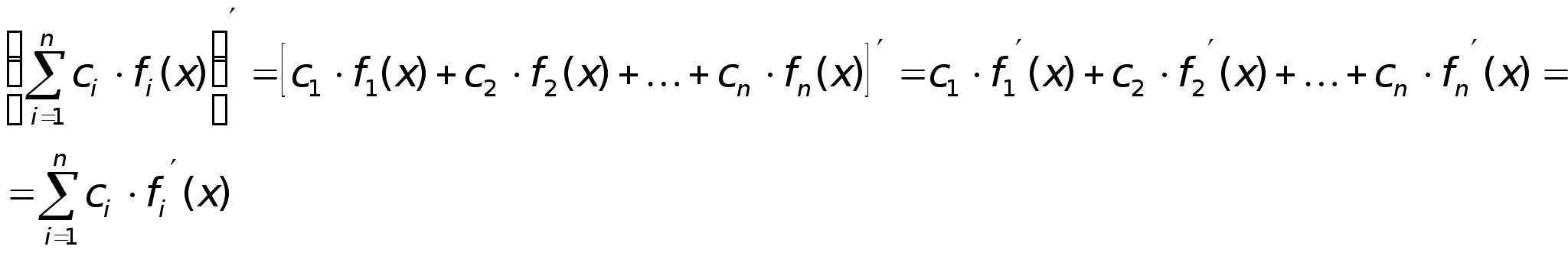
Производная от обратной ф-ии.
Dh:
Пусть
 в точке х0
имеет:
в точке х0
имеет:
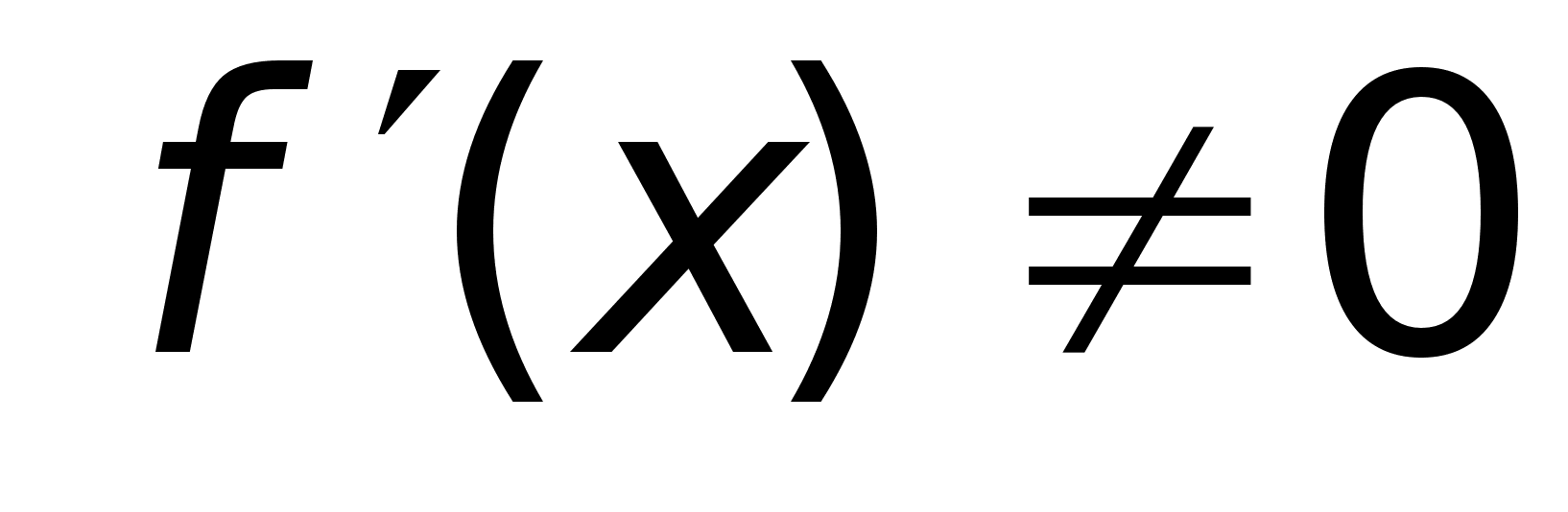
на промежутке, содержащем х0 , обратную ф-ию

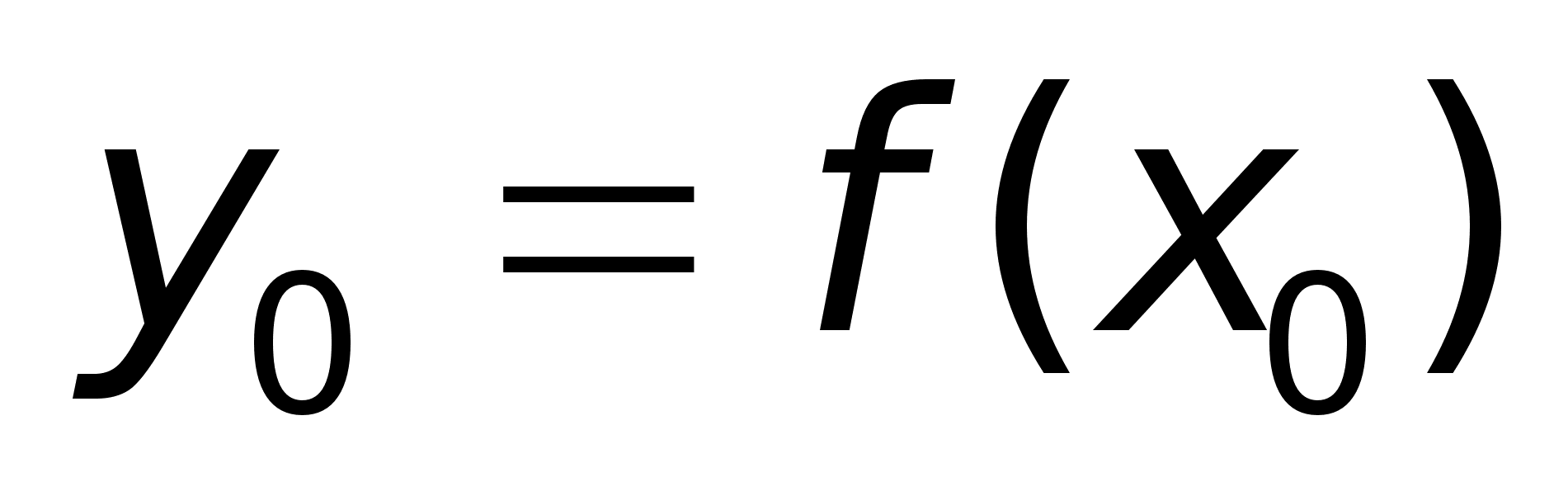
тогда в точке
х0
существует
 ,
равная
,
равная

Производная от обратной ф-ии.
Dh: Пусть
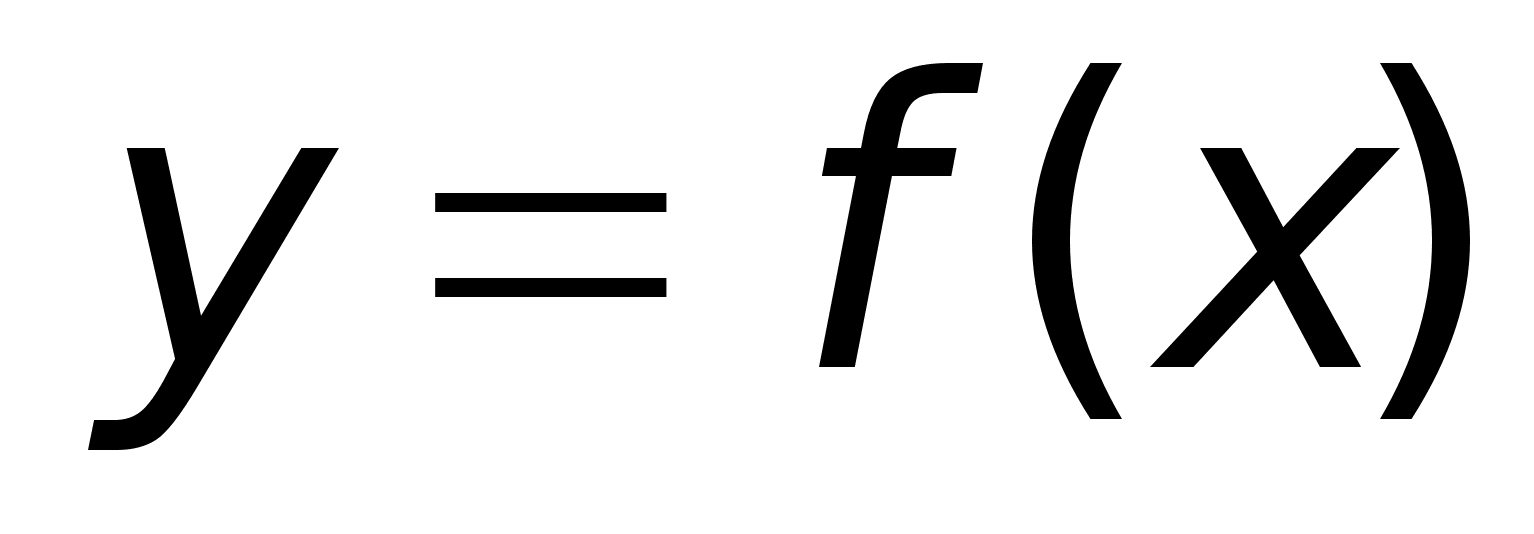 в точке х0
имеет:
в точке х0
имеет:

на промежутке, содержащем х0 , обратную ф-ию
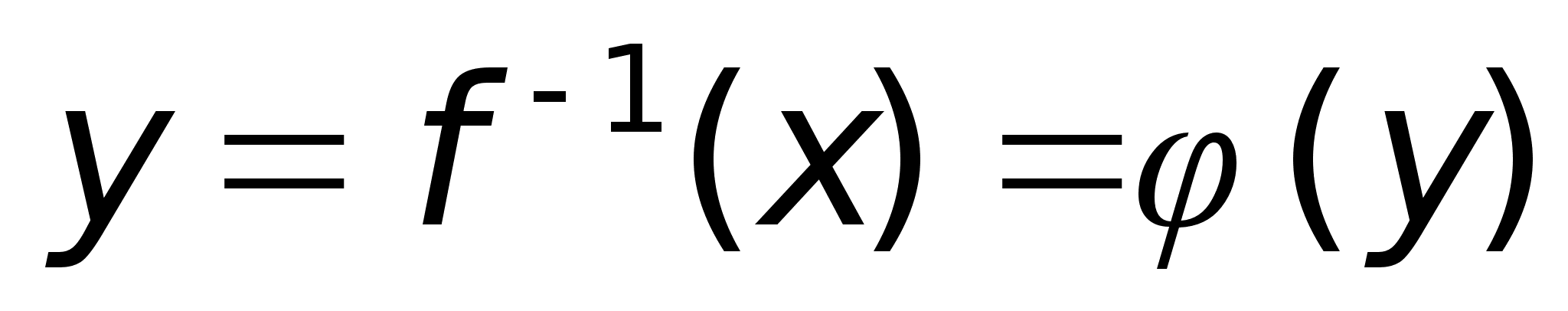
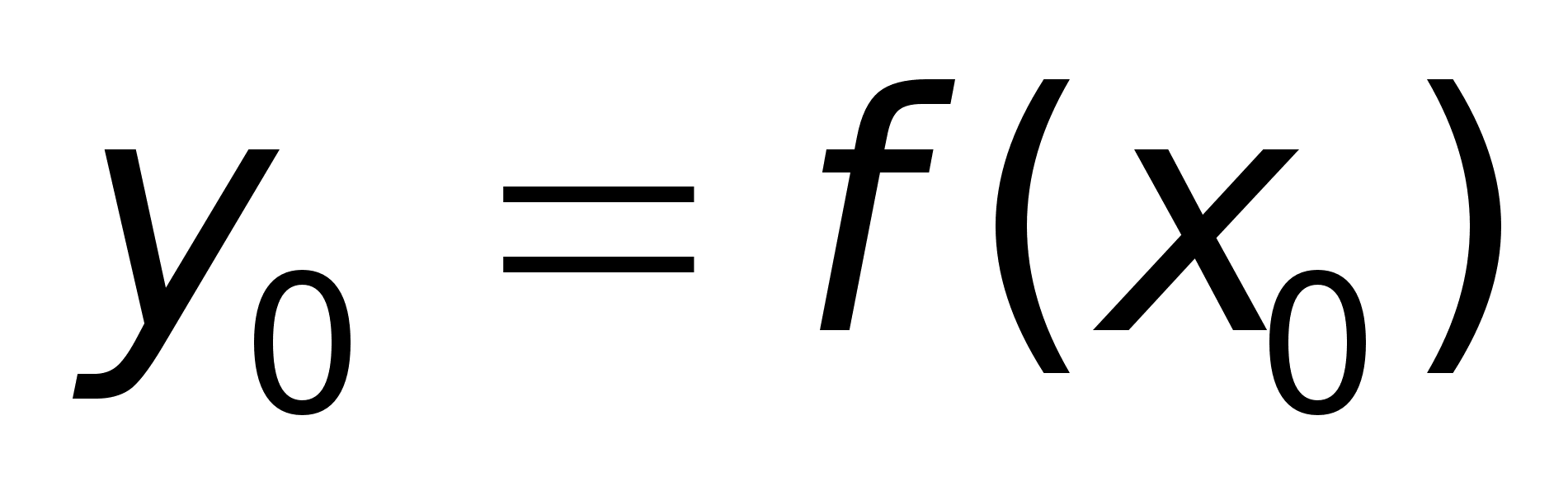
тогда в точке
х0
существует
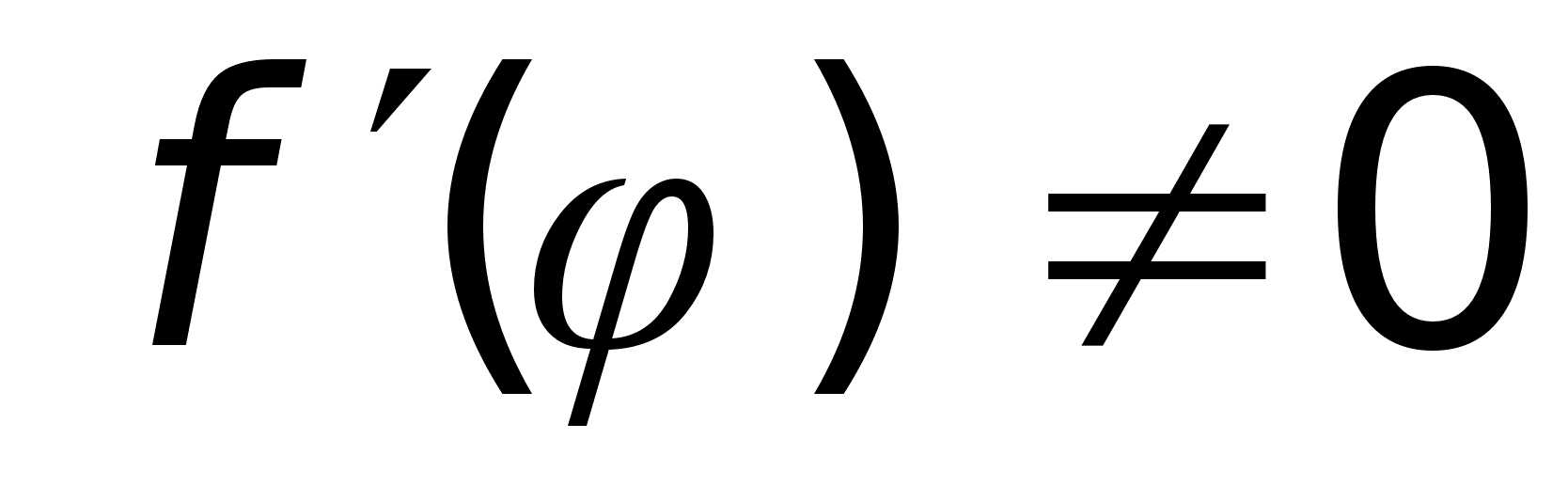 ,
равная
,
равная

Доказательство:
1. Пусть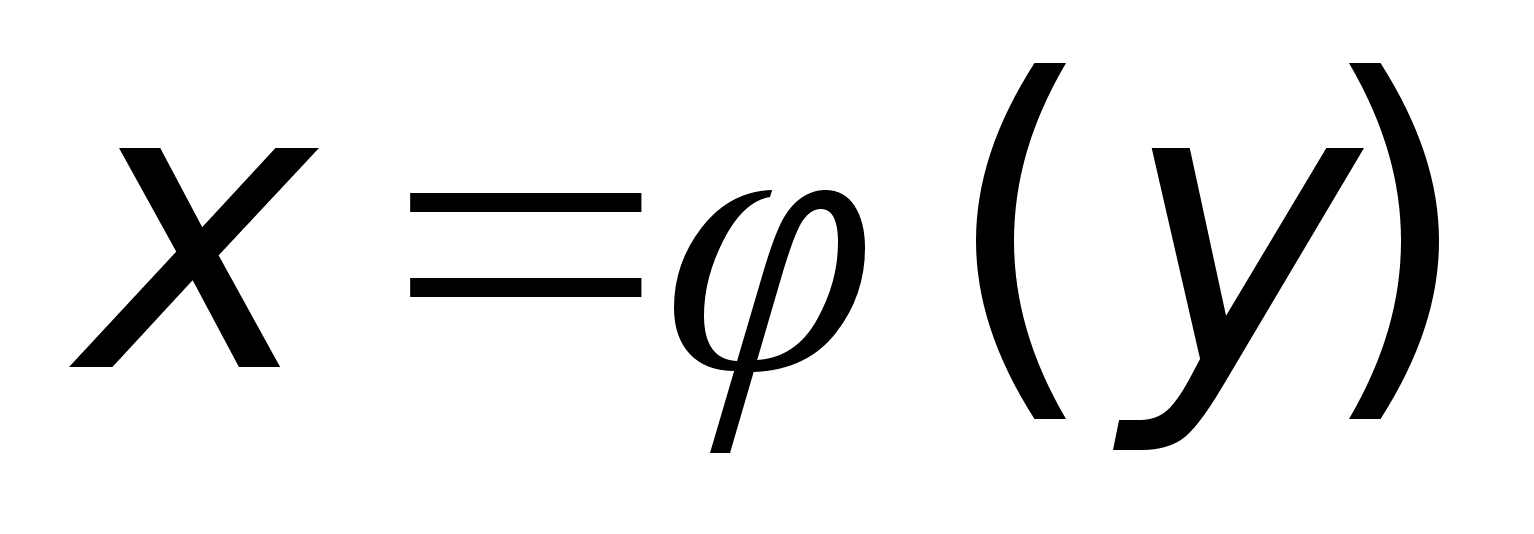 и
двум различным
значениям х
соответствует
е различных
значений y
.
и
двум различным
значениям х
соответствует
е различных
значений y
.
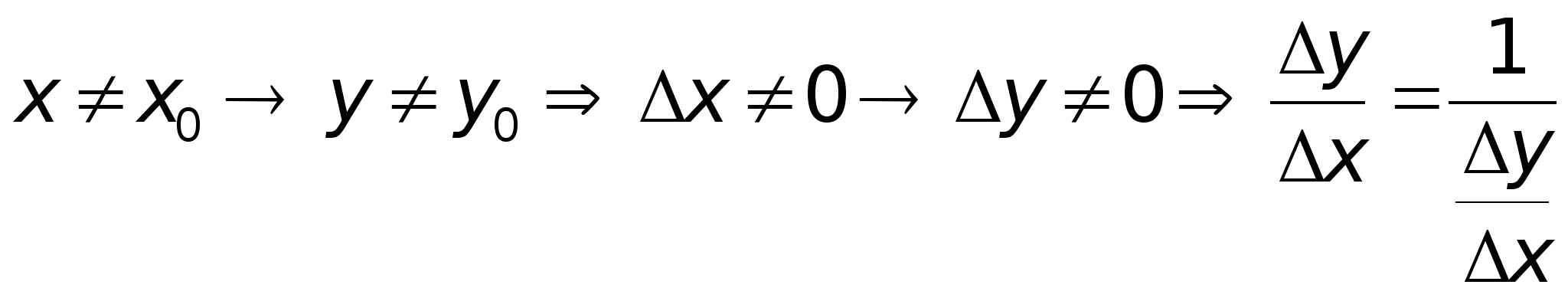
2. Пусть
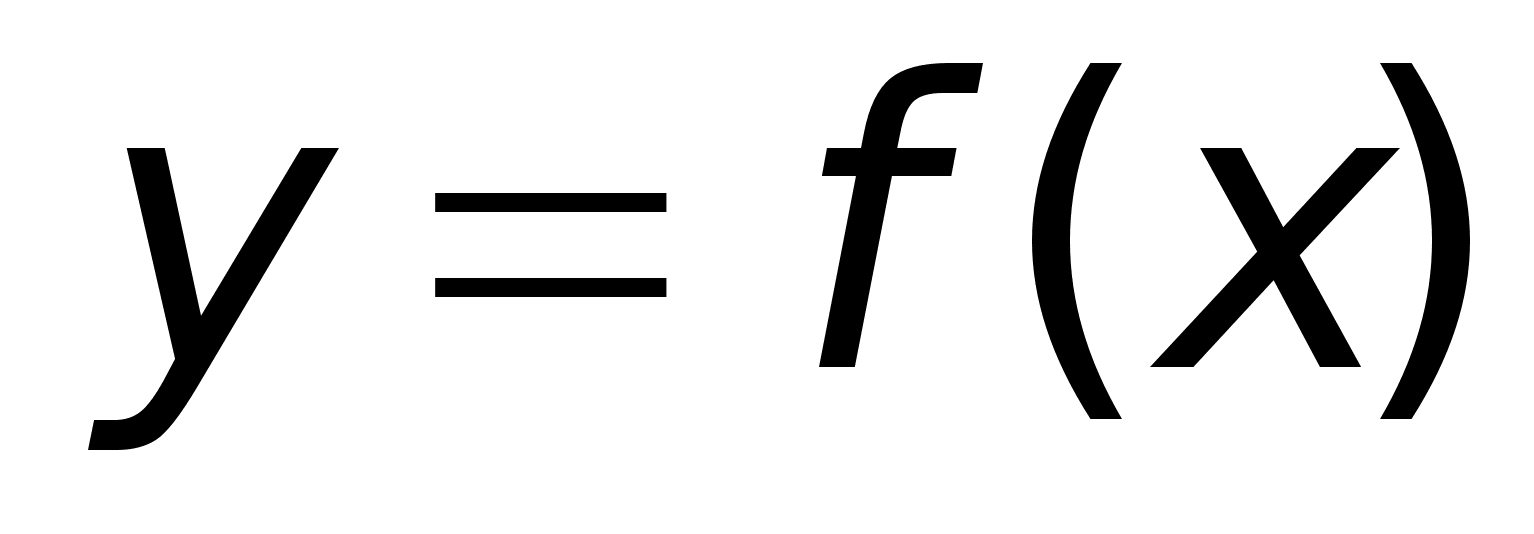 дифф. в точке
х0
, тогда
дифф. в точке
х0
, тогда
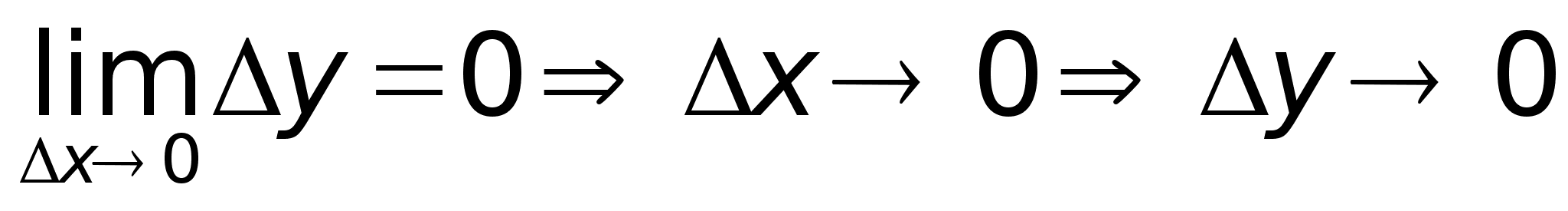

3. т.к.

Производная от сложной ф-ии.
Dh: Пусть:
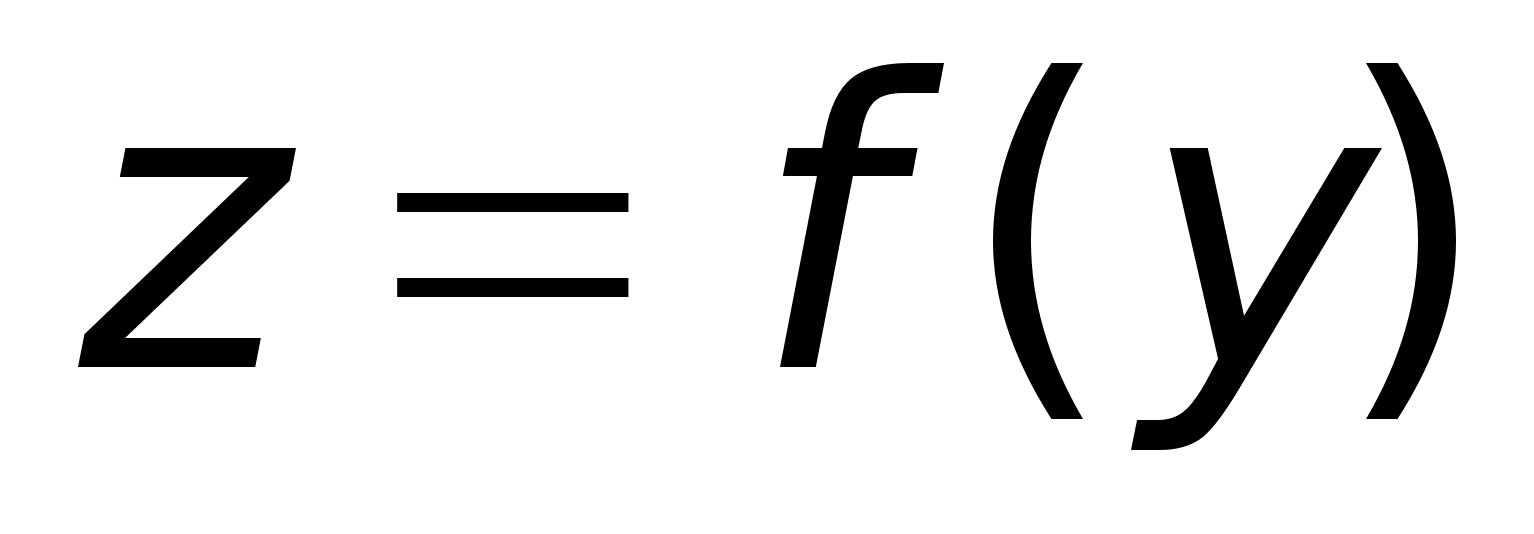 -
дифф. в точке
y0
.
-
дифф. в точке
y0
.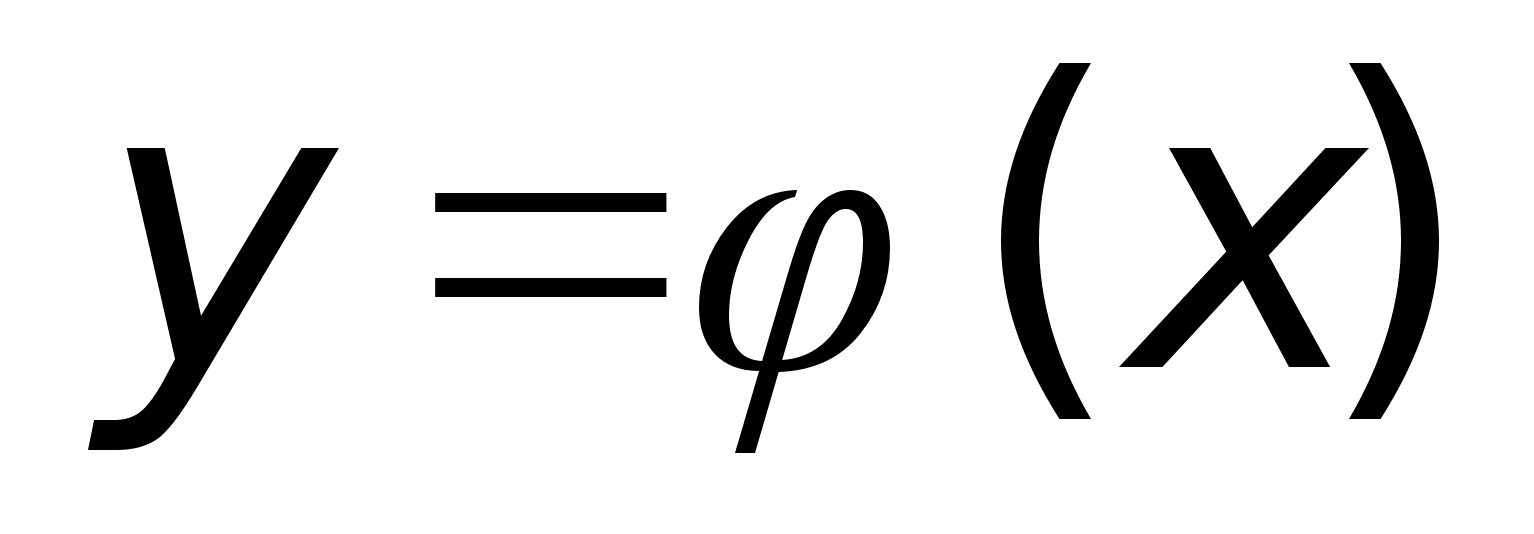 -
дифф. в точке
х0
.
-
дифф. в точке
х0
.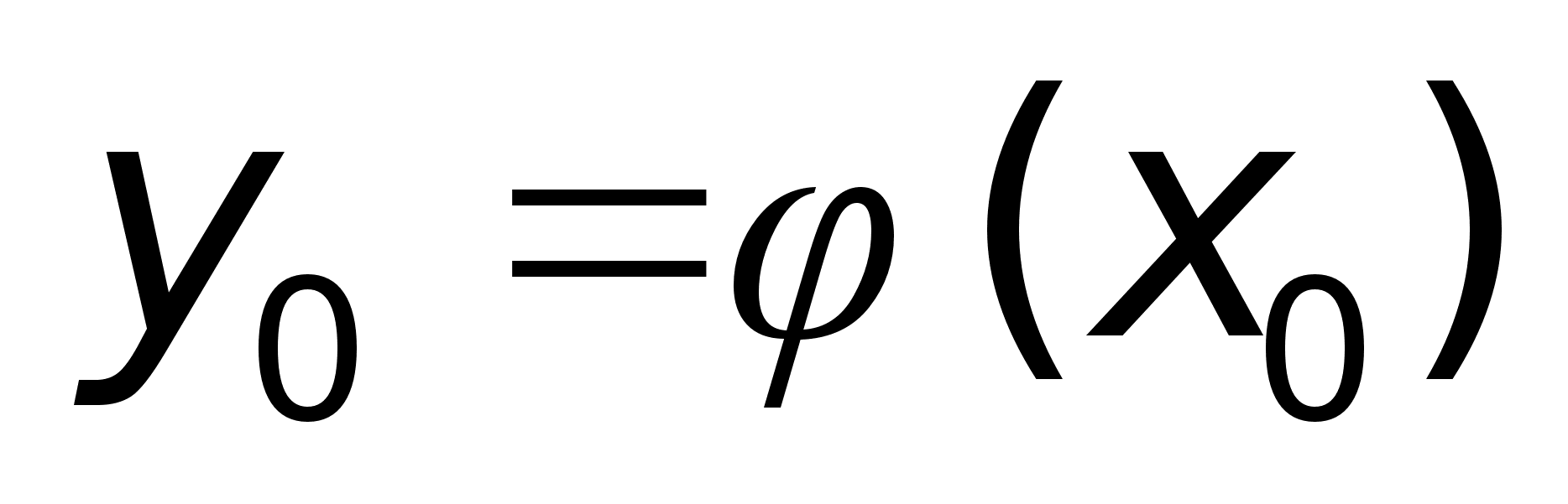
тогда сложная
ф-ия
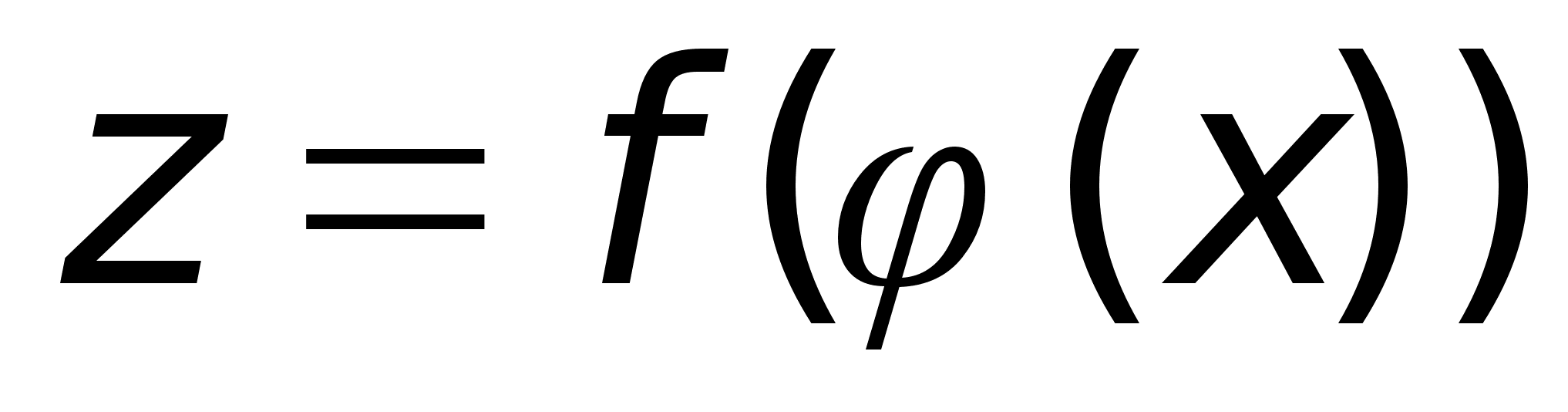 -
дифф. в точке
х0
и справедлива
формула:
-
дифф. в точке
х0
и справедлива
формула:

Доказательство:
1.
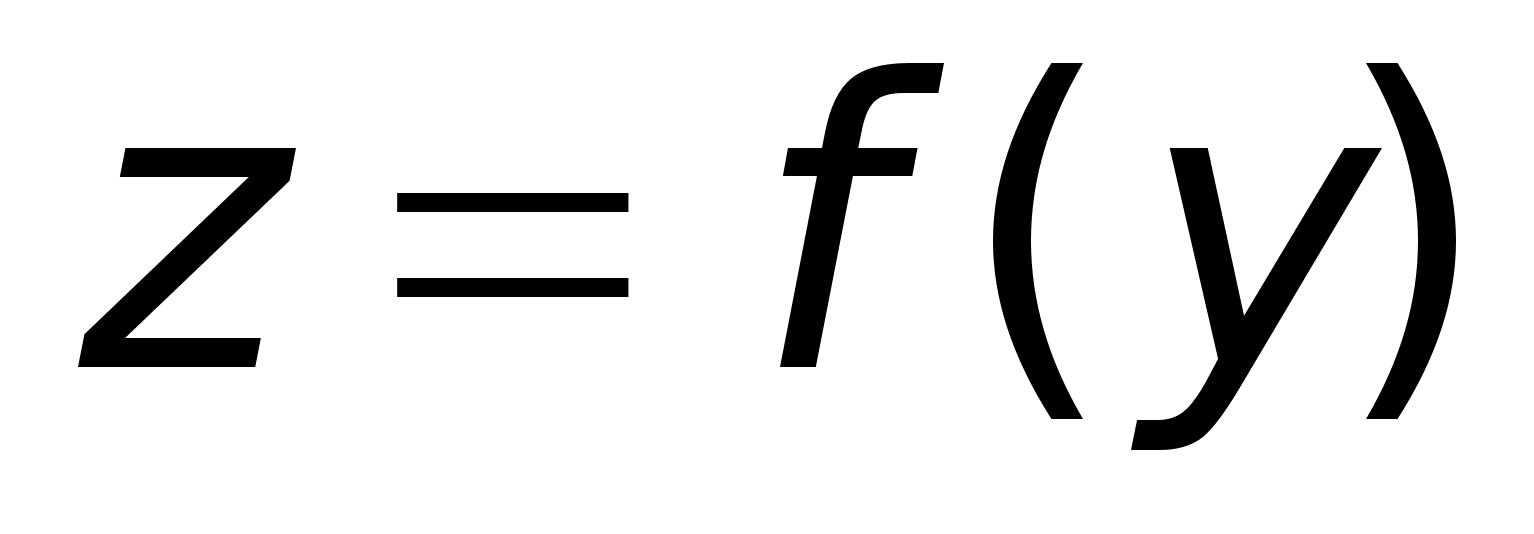 -
дифф. в точке
y0
-
дифф. в точке
y0

2.
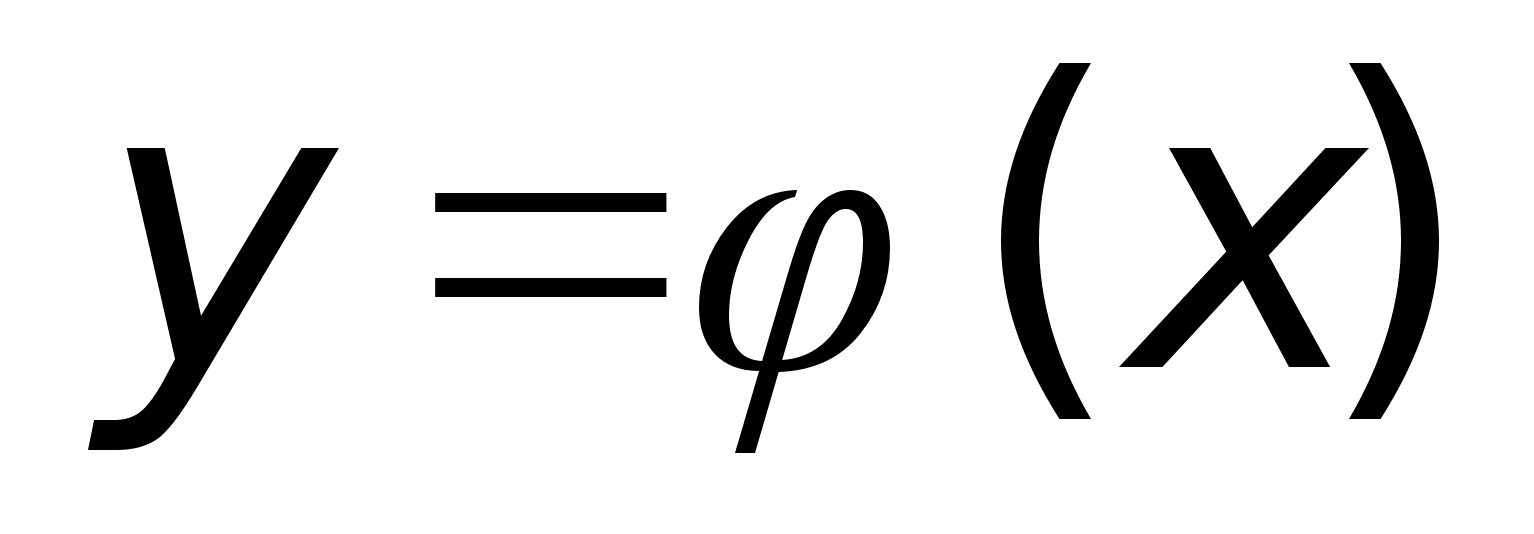 -
дифф. в точке
х0
-
дифф. в точке
х0
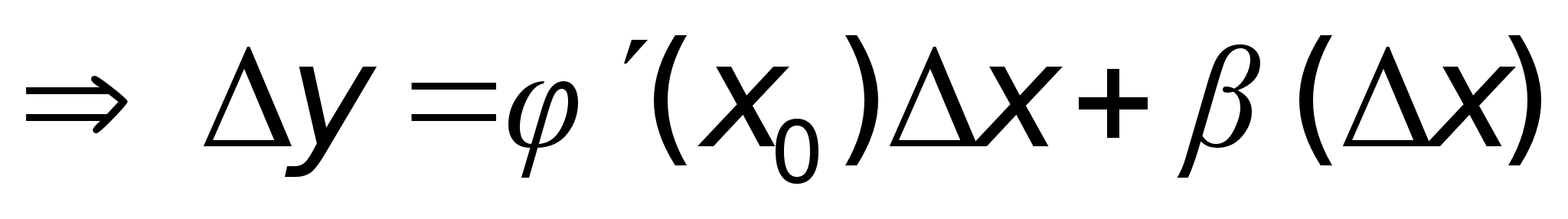
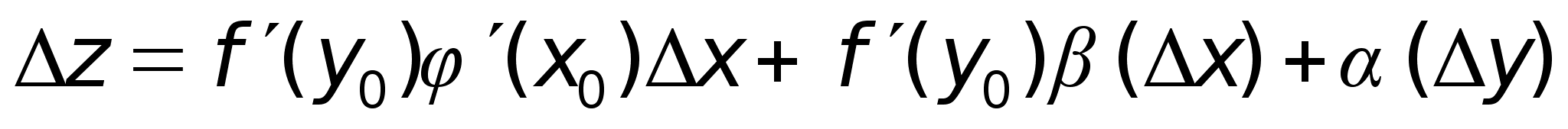
3.
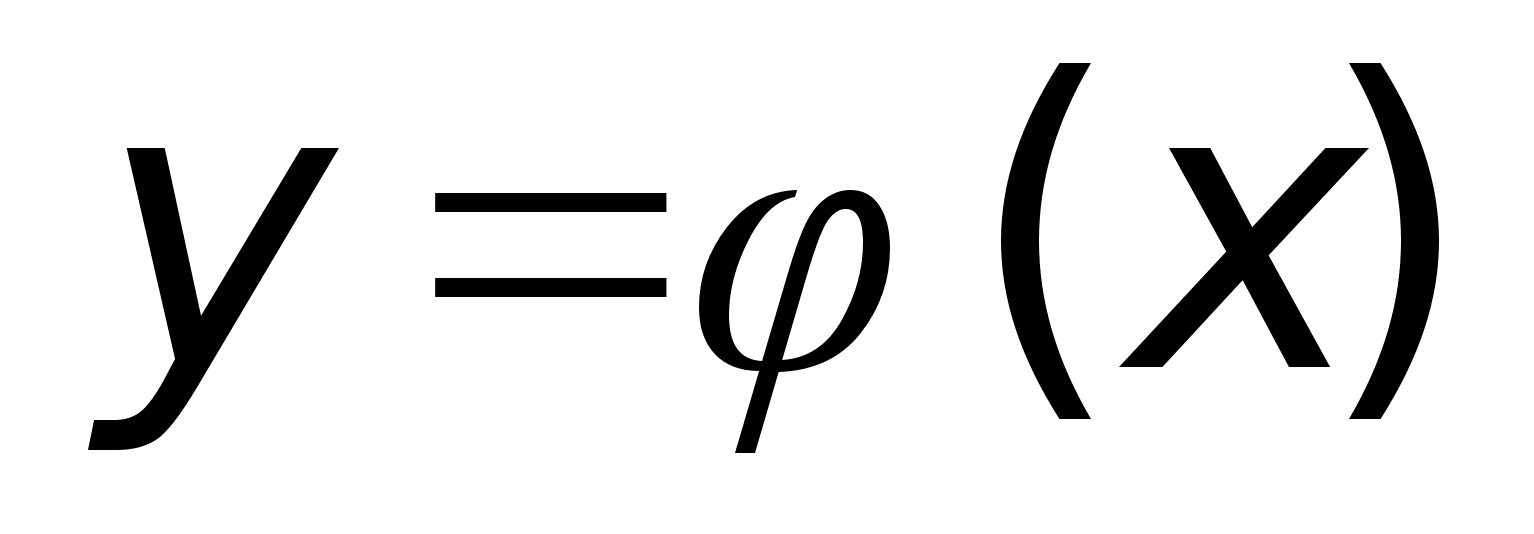 -
дифф. в точке
х0
а значит непрерывна
в этой точке
-
дифф. в точке
х0
а значит непрерывна
в этой точке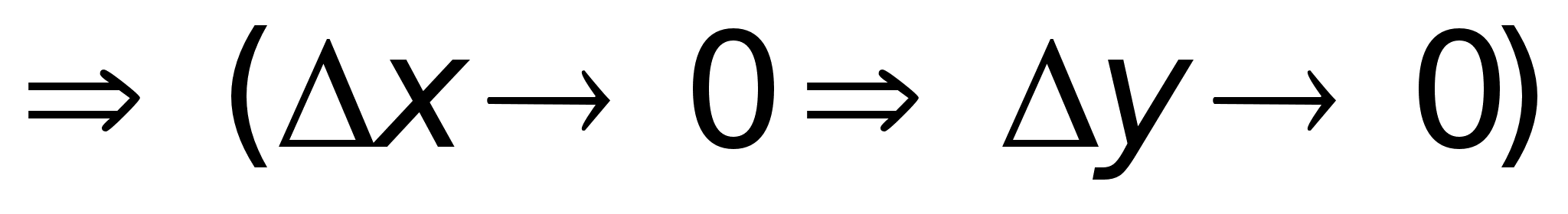 .
.
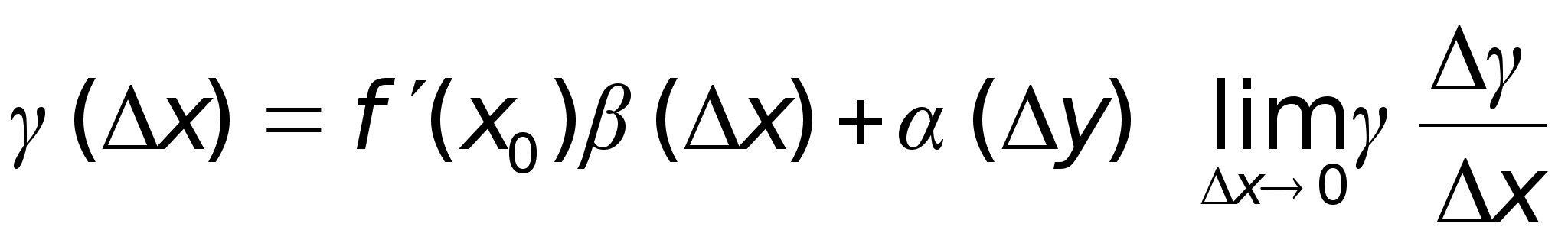

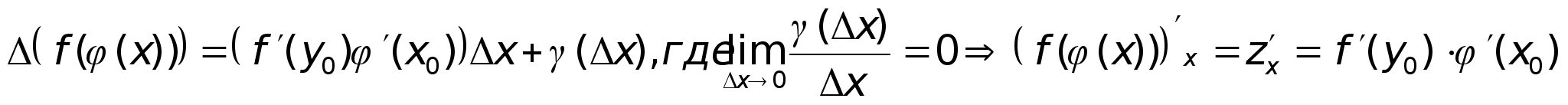
Односторонние производные.
Заменим в определении производной предел – односторонним пределом, получится определение односторонней производной.


Производная от параметрически заданной ф-ии.
Df: Ф-ия
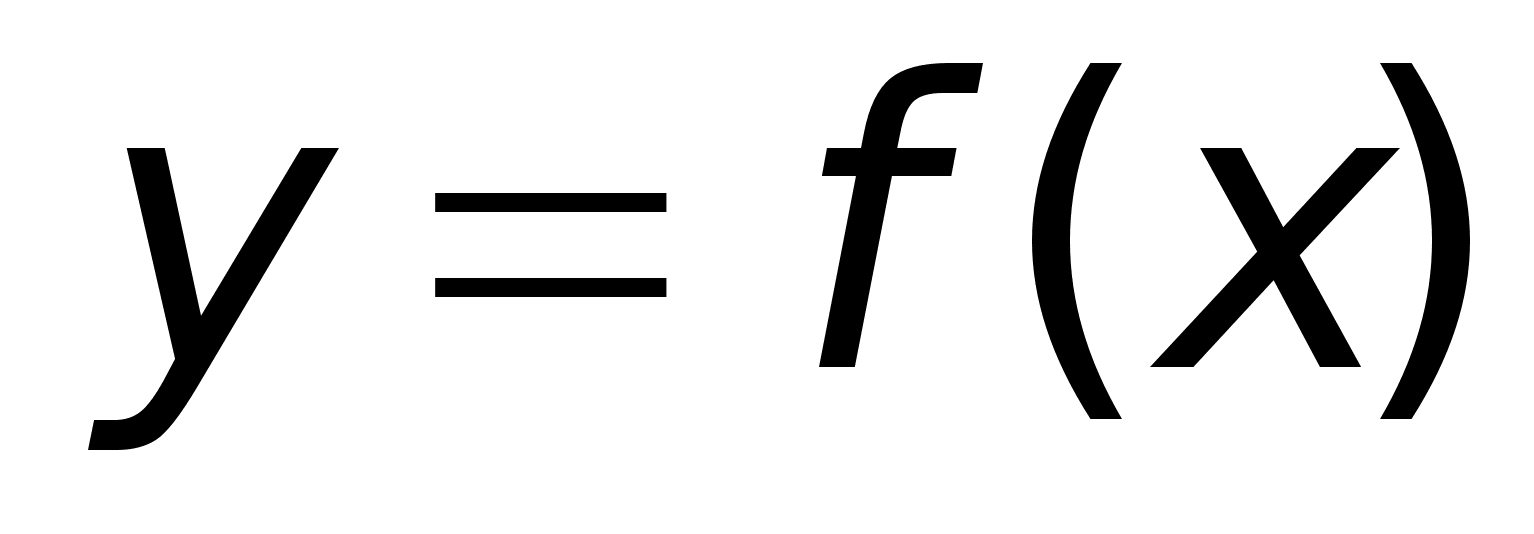 называется
заданной
параметрически,
если ее аналитическое
выражение может
быть представлено
в виде:
называется
заданной
параметрически,
если ее аналитическое
выражение может
быть представлено
в виде:
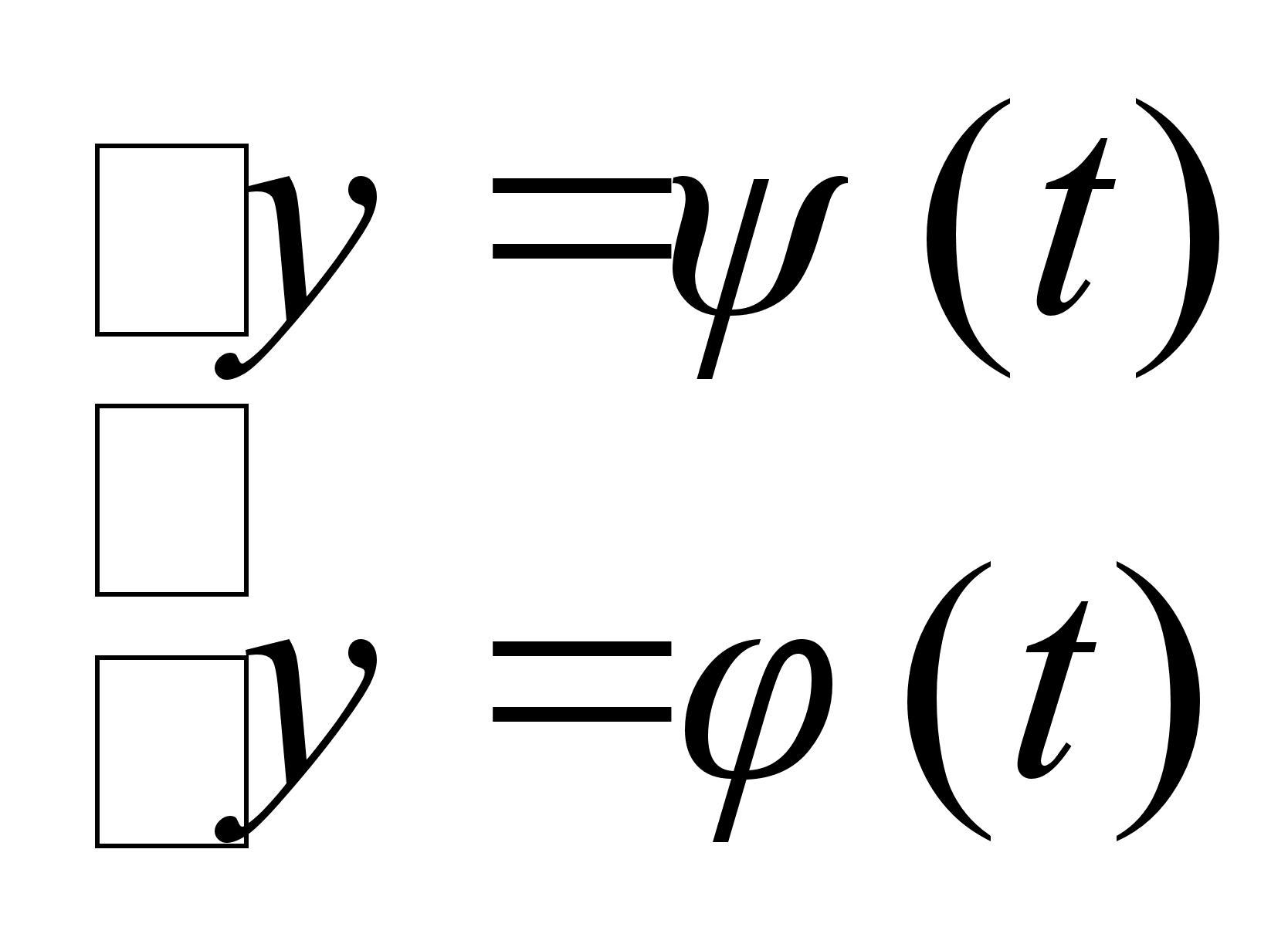 t- параметр.
t- параметр.
Dh: Пусть
ф-ия задана
параметрически,
где
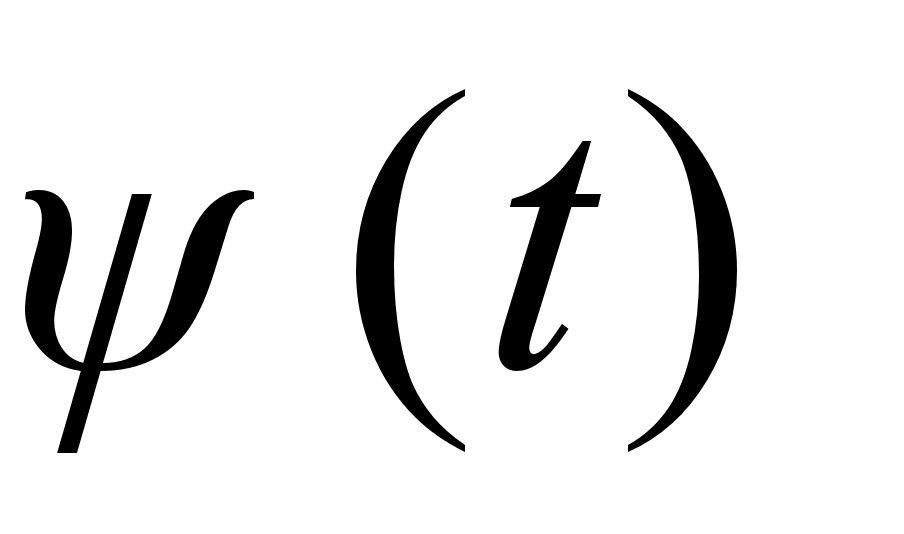 и
и
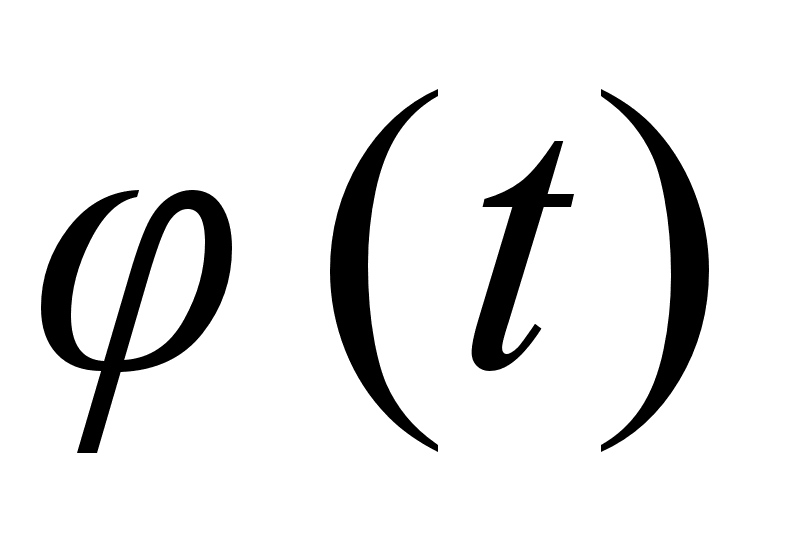 дифф. в точке
х0
, тогда
дифф. в точке
х0
, тогда
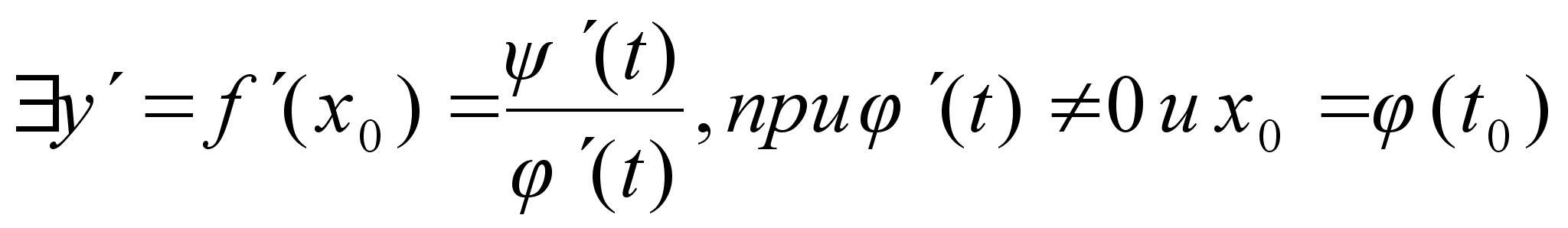
Доказательство:
Предположим.
что
 имеет обратную
ф-ию
имеет обратную
ф-ию
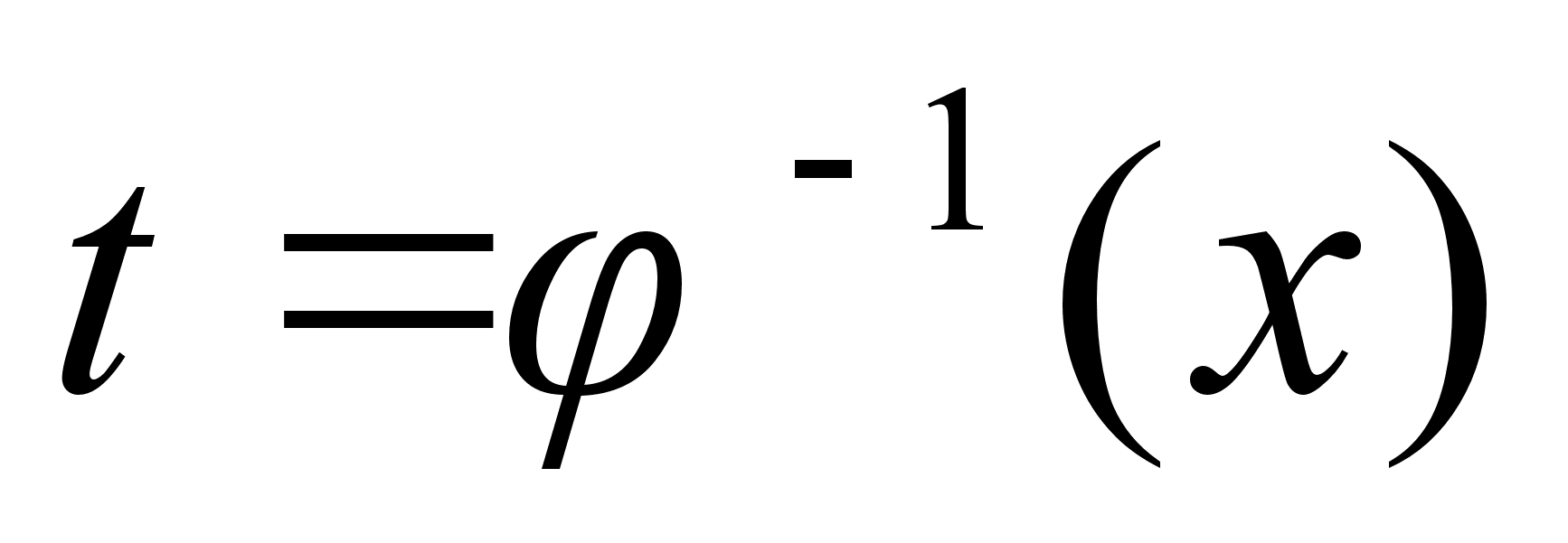 ,
тогда
,
тогда
 -
сложная ф-ия
от х
и определению
сложной ф-ии
имеет:
-
сложная ф-ия
от х
и определению
сложной ф-ии
имеет:
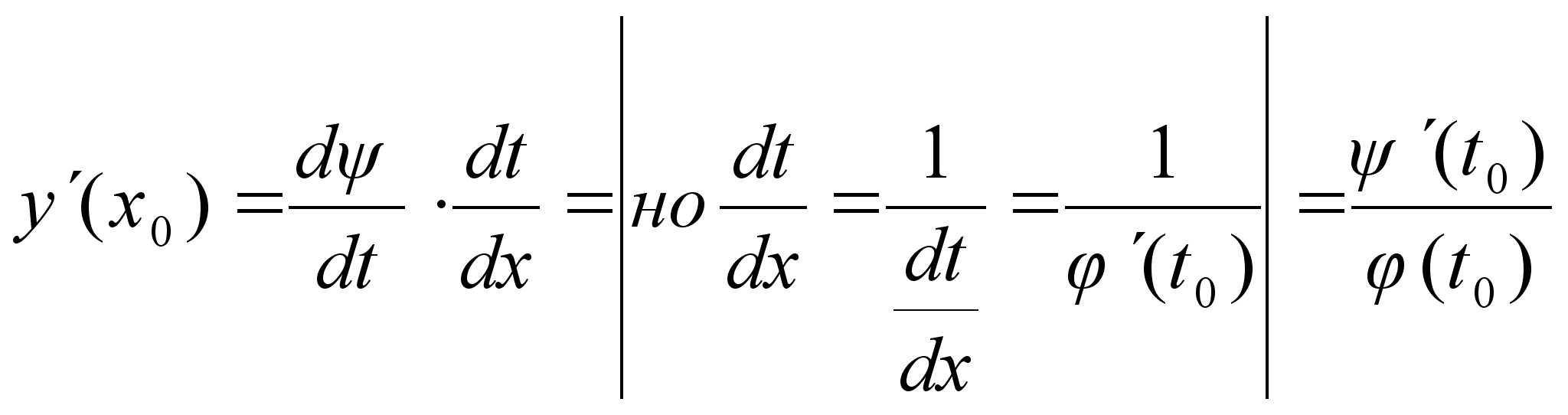
Производные высших порядков.
Df: Пусть
ф-ия
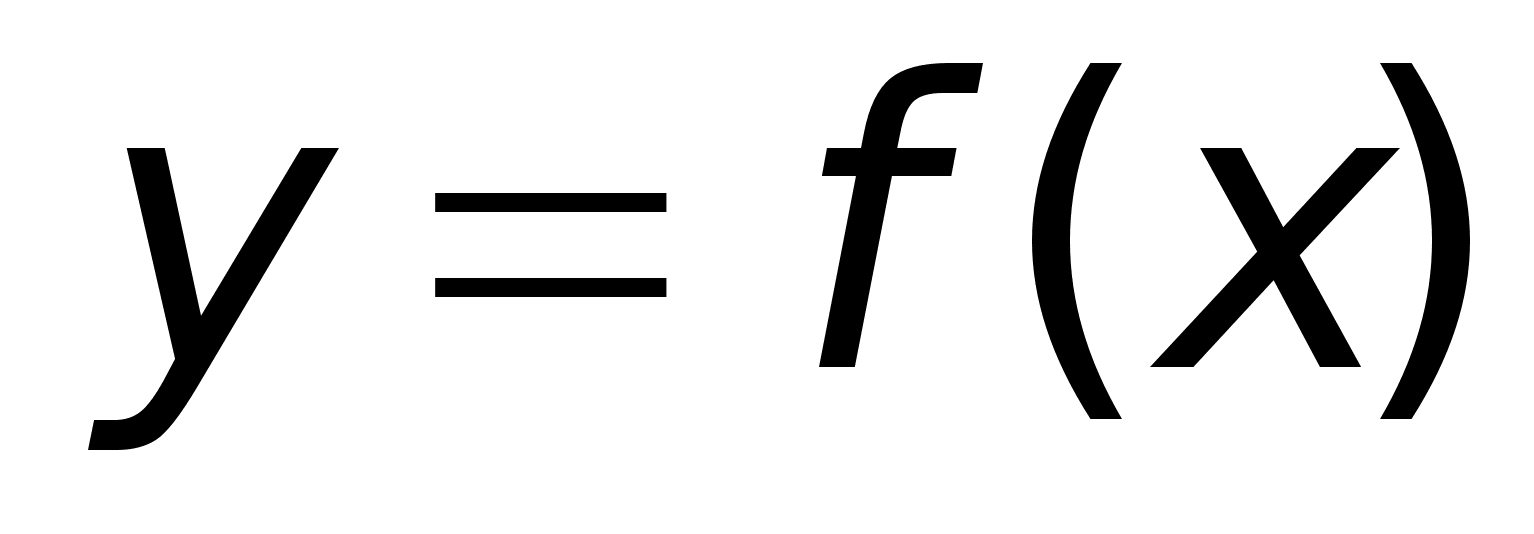 дифф. на Х
, то есть дифф.
в каждой т. Х
.
дифф. на Х
, то есть дифф.
в каждой т. Х
.
Каждому
значению Х
соответствует
единственное
значение
 ,
т.е. получаем
,
т.е. получаем
 как ф-ию, заданную
на Х.
как ф-ию, заданную
на Х.
Если она
окажется дифф.
на Х,
то мы можем
вычислить
следующую
 ,
которая будет
называться
второй и т.д.
,
которая будет
называться
второй и т.д.

Df: Производной
n-го
порядка от ф-ии
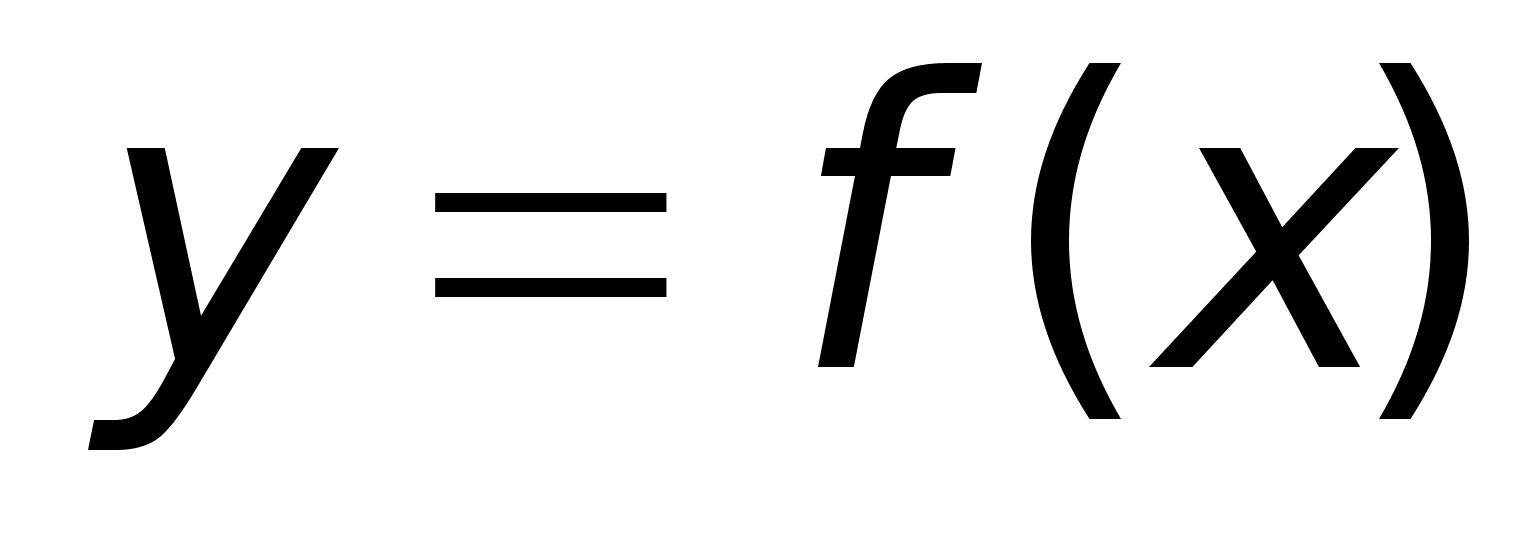 называется
первая производная
от производной
n-1 порядка.
называется
первая производная
от производной
n-1 порядка.
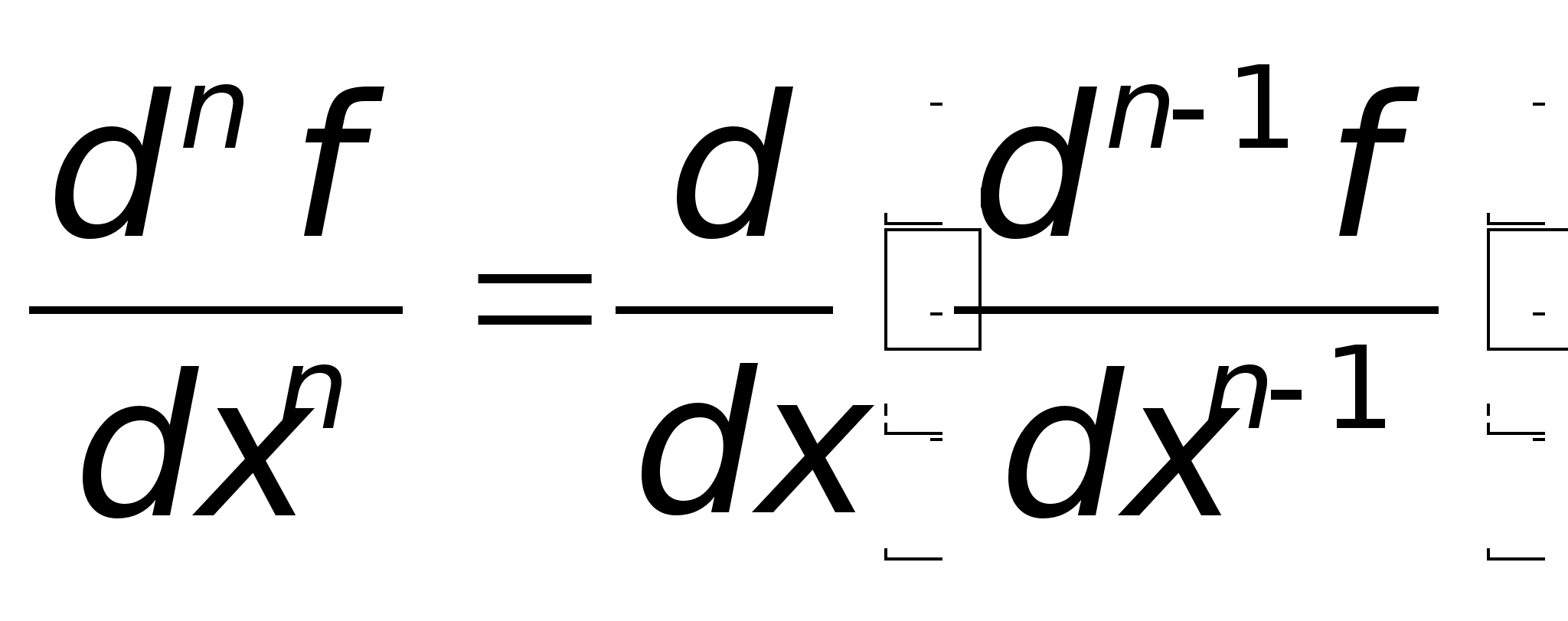
Пример:

Теоремы о дифф.

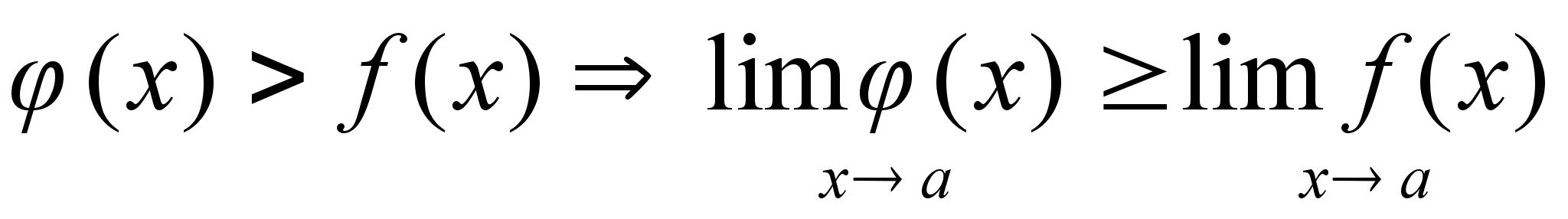
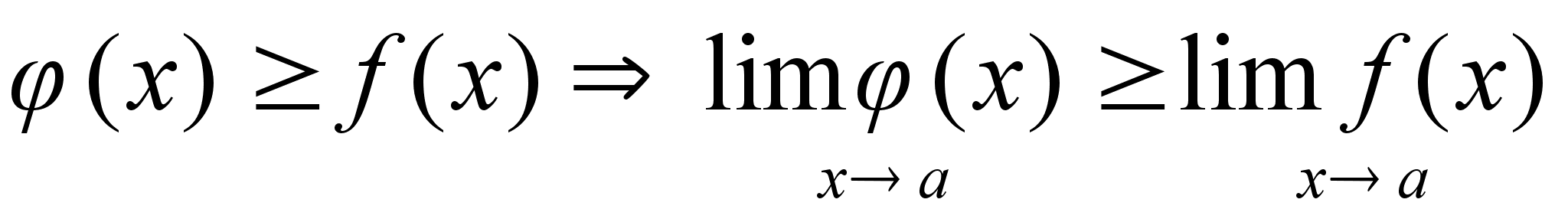
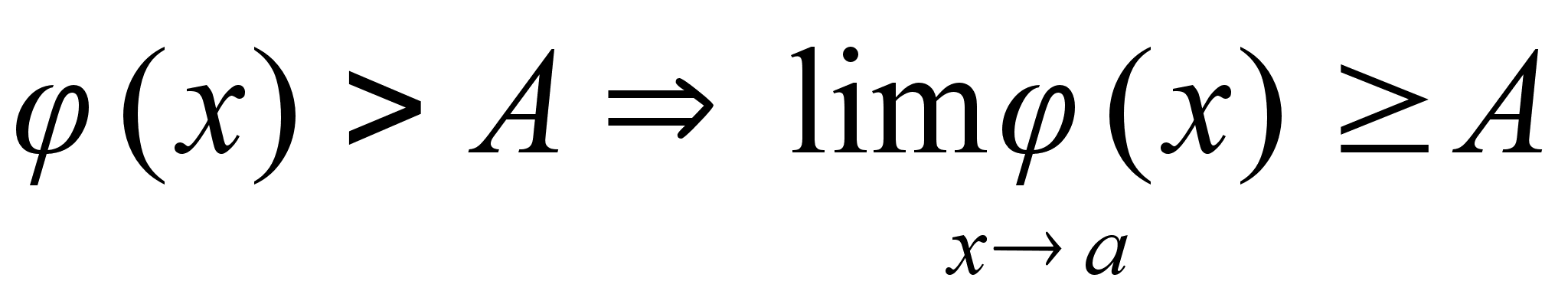
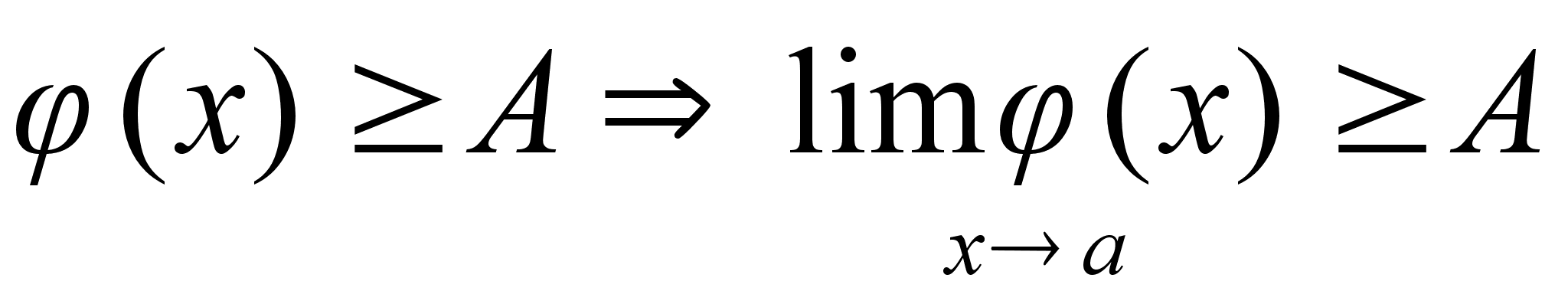
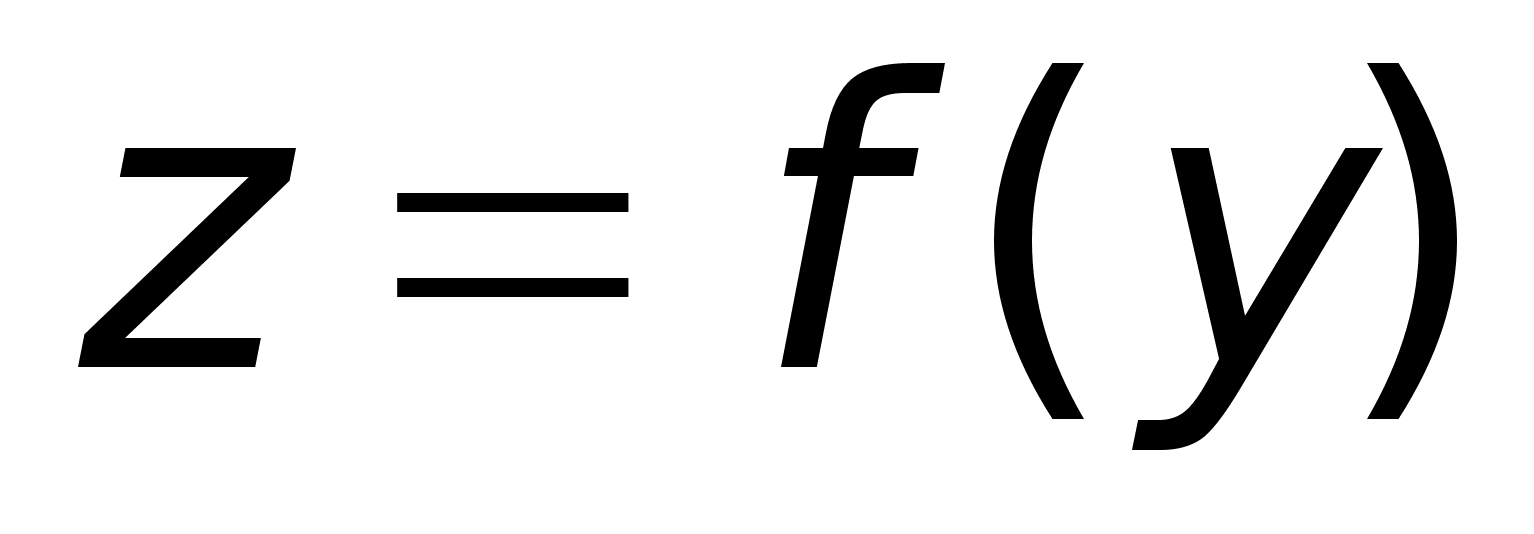 -
непрерывна
в т. y0
.
-
непрерывна
в т. y0
.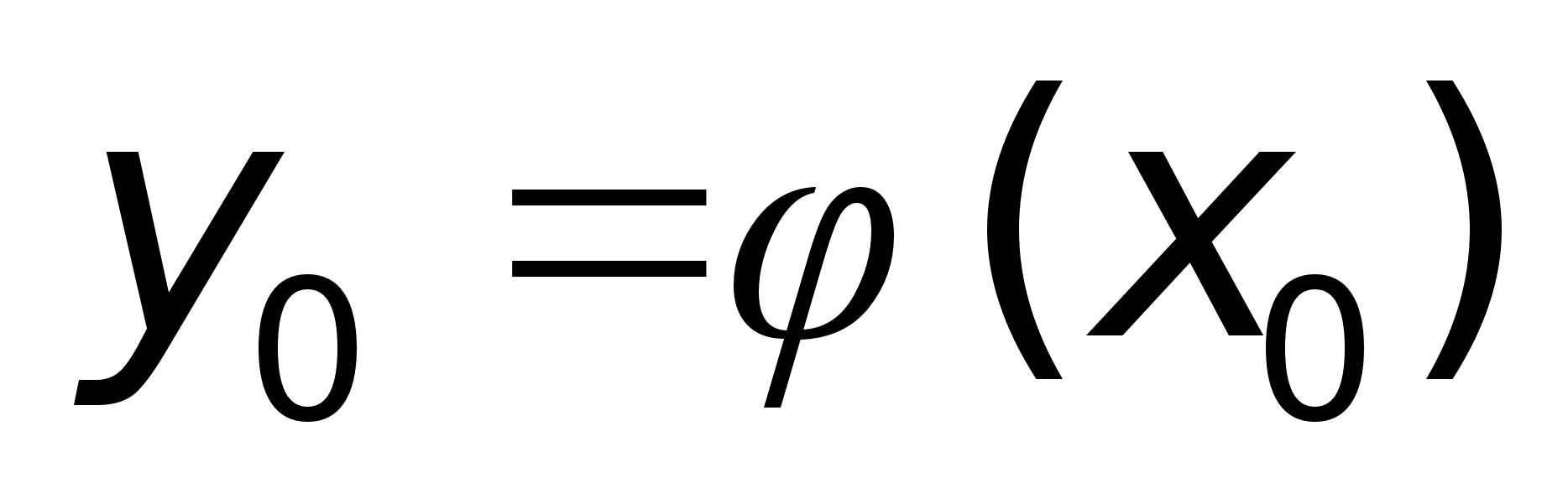
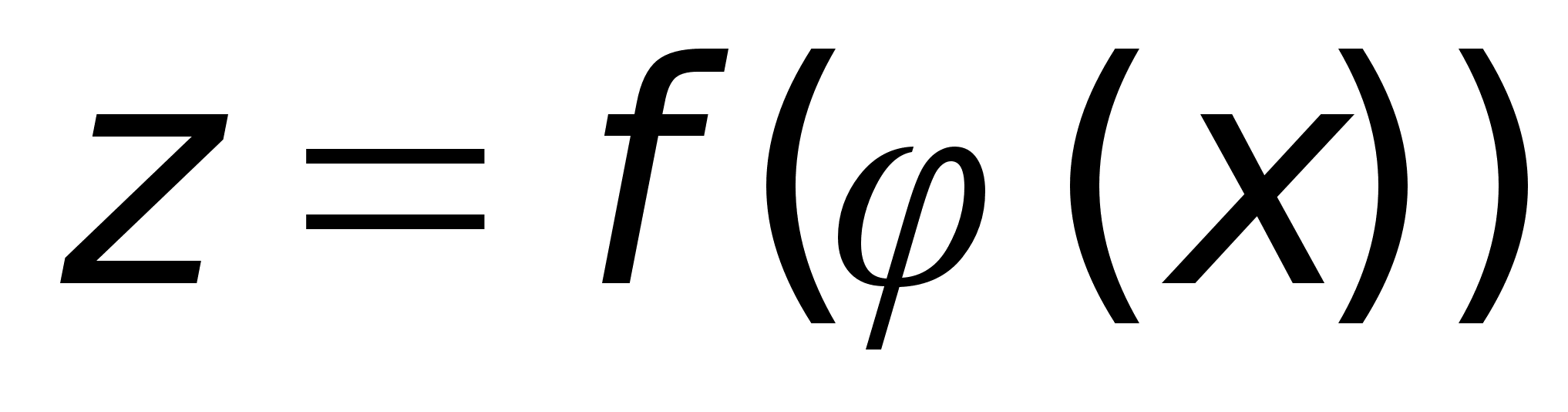 -
непрерывна
в т. х0
.
-
непрерывна
в т. х0
.