Розрахунок типових задач з математичної статистики
математичної статистики" width="597" height="485" align="BOTTOM" border="0" />Рис.4.1 Гістограма експериментального графіку функції щільності імовірності.
Аналізуємо обчислені оцінки математичного чекання та отриману гістограму.
Безперервна випадкова величина X приймає від’ємні значення. Отже, їй залишається бути розподіленою за нормальним (гаусовським) законом розподілення.
„Правило 3-х сігм” приблизно виконується (більшість значень дійсно лежить в інтервалі (-4.165276; 5.252514)). Відхилення практичної гістограми від теоретичної допоможе оцінити характеристика асиметрії та ексцес.
Таким чином, висуваємо гіпотезу H0 - випадкова величина X розподілена за нормальним законом розподілення.
Для обчислення теоретичних частот попадання випадкової величини X в коректований інтервал (з Таблиці 4.2) можна використовувати дві методики. Ми будемо застосовувати другу як більш теоретично обґрунтовану та правильнішу, а також точнішу.
Перша методика проста, але обчислення на її основі носять приблизний, оціночний характер. Перейдемо в обчисленнях від загальної до центрованої нормальної величини. Теоретично наша випадкова величина вважається розподіленою за загальним нормальним законом. Його функція щільності імовірності має в нашому випадку вигляд:
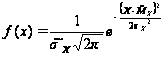 .
.
Перехід до центрованої нормальної величини:
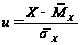 .
.
Функція щільності імовірності для неї:
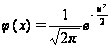 .
.
Таким чином
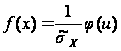 .
.
Імовірність попадання випадкової величини X в інтервал (Xi; Xi+1) дорівнює
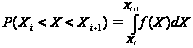 .
.
Дорівнює площі фігури, обмеженої графіком щільності імовірності, віссю 0X та прямими X=Xi, X=Xi+1.
Тобто можна приблизно вважати ії рівною добутку довжини інтервалу h на значення функції щільності імовірності в середині інтервалу (вищесказане є фактично двосторонньою оцінкою визначеного інтегралу):
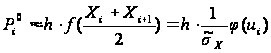 ,
,
де
значення
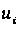 відповідає
середині інтервалу
відповідає
середині інтервалу
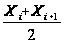 .
.
Знаючи теоретичну імовірність Pi, можна буде обчислити теоретичну кількість ni попадань випадкової величини X в і-й інтервал (Xi; Xi+1).
Але це буде дуже приблизна оцінка, бо коректування інтервалів розширило межі інтервалів та збільшило різницю між значеннями функції щільності імовірності в них. Точність цього методу обчислення теоретичних частот буде зростати при зменшенні інтервалу розбиття. Проте, це не можливо без порушення правила розбиття діапазону зміни значень випадкової величини в методі Пірсона. З загальних теоретичних відомостей імовірність попадання випадкової величини X в інтервал (Xi; Xi+1) можна виразити через функцію щільності імовірності
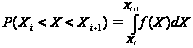 ,
,
або через функцію розподілення імовірності

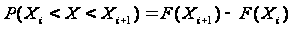 .
.
Для нормованого нормального розподілення функція розподілення імовірності обчислюється через функцію Лапласа (сама функція Лапласа не є функцією розподілення імовірності):
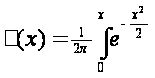 .
.
Значення функції Лапласа затабульовані, або ж їх можна підрахувати за допомогою математичних пакетів прикладних програм. Хоча з досить високою точністю можна й самому підрахувати значення функції Лапласа, використавши наступну наближену формулу (підінтегральну функцію було розкладено в ряд та взято інтеграл):
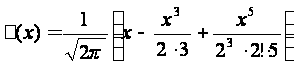 .
.
Функція розподілення імовірності нормального розподілення пов’язана з функцією Лапласа наступним співвідношенням:
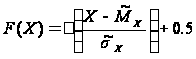 ,
якщо X>0,
,
якщо X>0,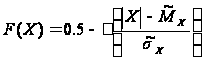 ,
якщо X<0.
,
якщо X<0.
Знову перейдемо в обчисленнях від загальної до центрованої нормальної величини:
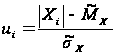 .
.
Це зафіксовано у п’ятій строчці Таблиці 4.2. Тоді імовірність попадання випадкової величини X в інтервал (Xi; Xi+1) можна виразити через функцію Лапласа так:
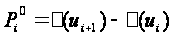 ,
,
де
значення
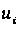 - нормована
нормальна
випадкова
величина, що
відповідає
Xi
(результат
занесено в
шосту строчку
Таблиці 4.2). Знаючи
теоретичну
імовірність
Pi0,
можна буде
обчислити
теоретичну
кількість ni0
попадань випадкової
величини X в
і-й інтервал
(Xi;
Xi+1)
з Таблиці 4.2 (і
результат
занесено у
відповідну
сьому строчку
Таблиці 4.2).
- нормована
нормальна
випадкова
величина, що
відповідає
Xi
(результат
занесено в
шосту строчку
Таблиці 4.2). Знаючи
теоретичну
імовірність
Pi0,
можна буде
обчислити
теоретичну
кількість ni0
попадань випадкової
величини X в
і-й інтервал
(Xi;
Xi+1)
з Таблиці 4.2 (і
результат
занесено у
відповідну
сьому строчку
Таблиці 4.2).
Таблиця 4.1 Інтервали розбиття
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| (-5; - 4) | (-4; - 3) | (-3; - 2) | (-2; - 1) | (-1; 0) |
(0; 1) |
(1; 2) |
(2; 3) |
(3; 4) |
(4; 5) |
(5; 6) |
| 1 | 2 | 1 | 14 | 18 | 22 | 25 | 15 | 1 | 0 | 1 |
| 0.01 | 0.02 | 0.01 | 0.14 | 0.18 | 0.22 | 0.25 | 0.15 | 0.01 | 0 | 0.01 |
Таблиця 4.2 Розраховані імовірності
| I | 1 | 2 | 3 | 4 | 5 |
| (Xi; Xi+1) | (-5; - 1) | (-1; 0) |
(0; 1) |
(1; 2) |
(2; 6) |
| ni | 18 | 18 | 22 | 25 | 17 |
|
|
0.18 | 0.18 | 0.22 | 0.25 | 0.17 |
| (ui; ui+1) | (2.8395; 0.2969) | (0.2969; 0) | (0; 0.2969) | (0.2969; 0.9322) | (0.9322; 3.4752) |
| Pi0 | 0.3798 | 0.1179 | 0.1179 | 0.2059 | 0.1760 |
| ni0 | 38 | 12 | 12 | 21 | 18 |
Обчислили значення критерію збіжності Пірсона. В нашому випадку він дорівнюватиме:
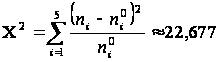 .
.
Робимо висновок про збіжність закону розподілення практичних даних та закону розподілення, що відповідає висунутій гіпотезі H0.
Кількість ступенів свободи k = s - 1 - r, де s=5 - число інтервалів розбиття діапазону значень випадкової величини X, r=2 - число параметрів розподілення, що були оцінені за даними вибірки і використовувалися при підрахункові теоретичних ймовірностей (для нормального розподілення це математичне чекання та середньоквадратичне відхилення), дорівнює k = 5 - 3 =2.
За
таблицею розподілення
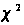 з k ступенями
свободи знаходимо
з k ступенями
свободи знаходимо
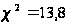 при α=0.001
(більш точні
дані відсутні).
Тобто практичні
дані узгоджуються
з гіпотезою
H0
з імовірністю
більш ніж 0.999.
при α=0.001
(більш точні
дані відсутні).
Тобто практичні
дані узгоджуються
з гіпотезою
H0
з імовірністю
більш ніж 0.999.
Висока імовірність узгодженості практичних даних з теоретичними дає підставу перевірити та оцінити потужність критерію (імовірність прийняття альтернативних гіпотез).
Висновки
У виконаній курсовій роботі наведено огляд теоретичних відомостей з курсу Теорії ймовірностей та математичної статистики, визначено алгоритм виконання типових завдань з Теорії ймовірностей. І також виконано розрахунок типової задачі з визначення законів розподілення випадкових величин.
Список літератури
В.В. Гнеденко. Курс теории вероятностей. М. - Наука, 1988.
В.П. Чистяков. Курс теории вероятностей. М. - Наука, 1982.
А.А. Боровков. Теория вероятностей.М. - Наука, 1988.
Б.А. Севастьянов. Курс теории вероятностей и математической статистики.М. - Наука, 1982.
Сборник задач по теории вероятностей, математической статистике и теории случайных функций (под редакцией А.А. Свешникова).
И.Н. Коваленко, А.А. Филлипов. Теория вероятностей и математическая статистика. М. - Высшая школа, 1988.
Е.С. Вентцель. Теория вероятностей. М. - Наука, 1969.
И.И. Гихман, А.В. Скороход, М.И. Ядренко. Теория вероятностей и математическая статистика. Киев - Высшая школа, 1979.
И.И. Гихман, А.В. Скороход. Введение в теорию случайных процессов.М. - Наука, 1969.
А.Т. Гаврилин, О.Н. Репин, И.П. Смирнов. Задачи по теории вероятностей, математической статистике и теории случайных процессов. Методическая разработка для студентов дневного отделения радиофизического факультета. Горький, ГГУ, 1983.
Г.И. Агапов. Задачник по теории вероятностей. М. - Высшая школа, 1994.
Большев Л.Н., Смирнов Н.В. Таблицы математической статистики. М.: Наука, 1965.
Боровков А.А. Математическая статистика. М.: Наука, 1984.
Коршунов Д.А., Чернова Н.И. Сборник задач и упражнений по математической статистике. Новосибирск: Изд-во Института математики им. С.Л. Соболева СО РАН, 2001.
Феллер В. Введение в теорию вероятностей и ее приложения. М.: Мир, Т.2, 1984.