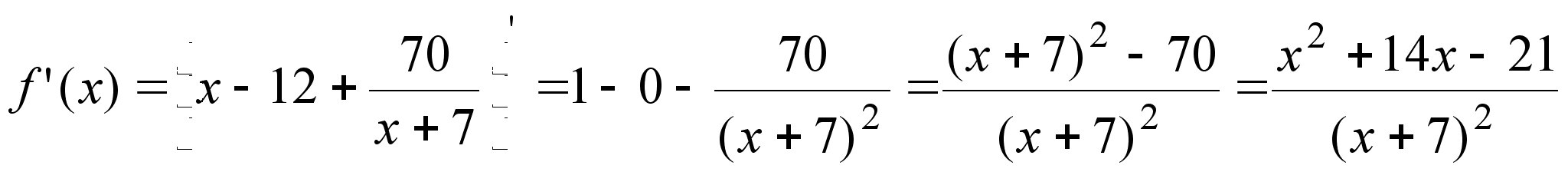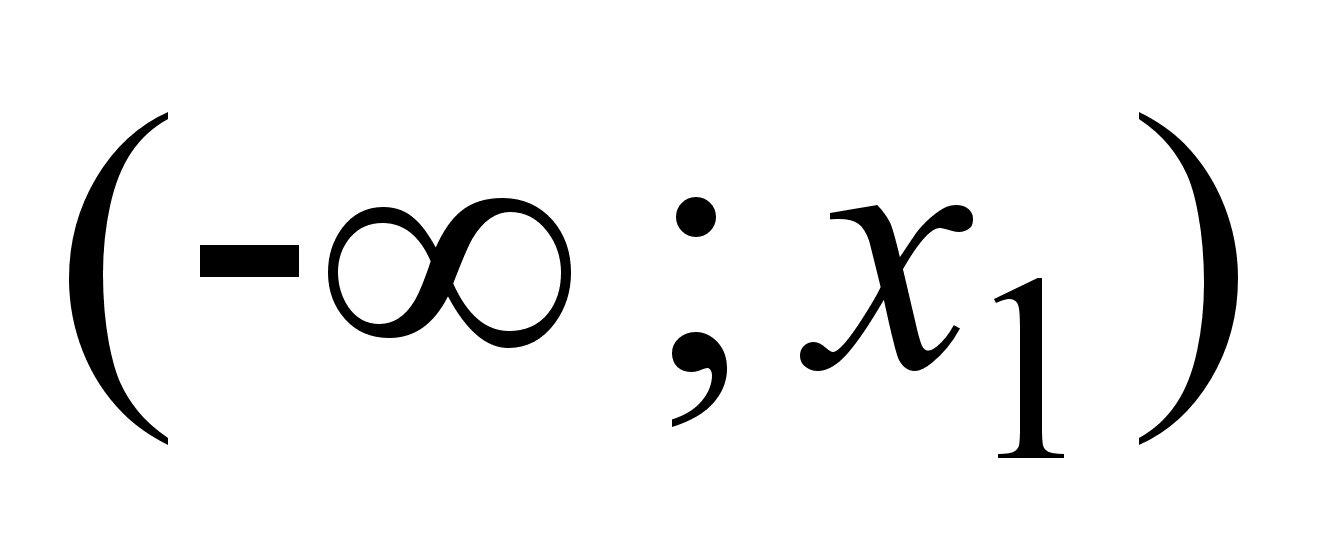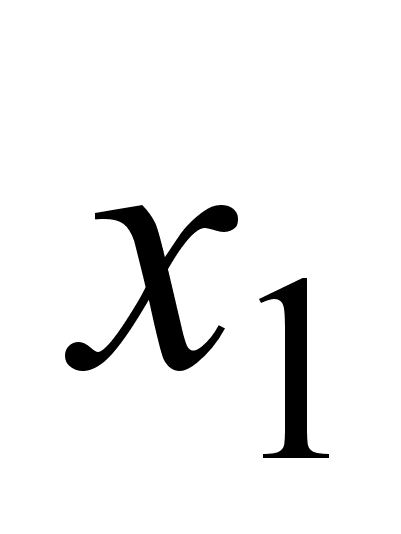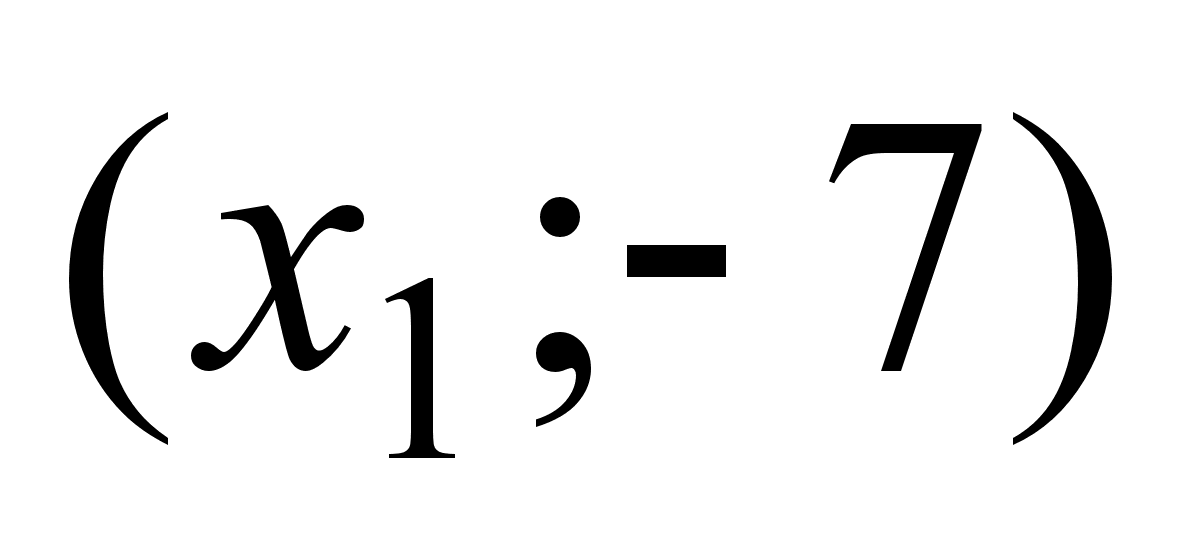Методические указания по курсу Математика для студентов I курса исторического факультета
height="61" align="LEFT" hspace="13" /> 
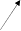 z
z
y

v
v
x |
y |
y |
x y |
z y (x y) |
t (x z) |
v ( x y ) |
Ответ: t v |
|
И И Л Л |
И Л И Л |
Л И Л И |
И И И Л |
Л И Л Л |
Л И И И |
И И Л И |
Л И Л И |
Б. Проверить, является ли формула (x y) (x y)) (x y) тавтологией.
Решение (аналогично решению предыдущей задачи, отличается лишь v: x y.
x |
y |
y |
x y |
z y (x y) |
t x z |
v x y |
Ответ: t v |
|
И И Л Л |
И Л И Л |
Л И Л И |
И И И Л |
Л И Л Л |
Л И И И |
Л И И И |
И И И И |
Ответ: да, тавтология.
Задание 5.
Построить
график дробно-рациональной
функции
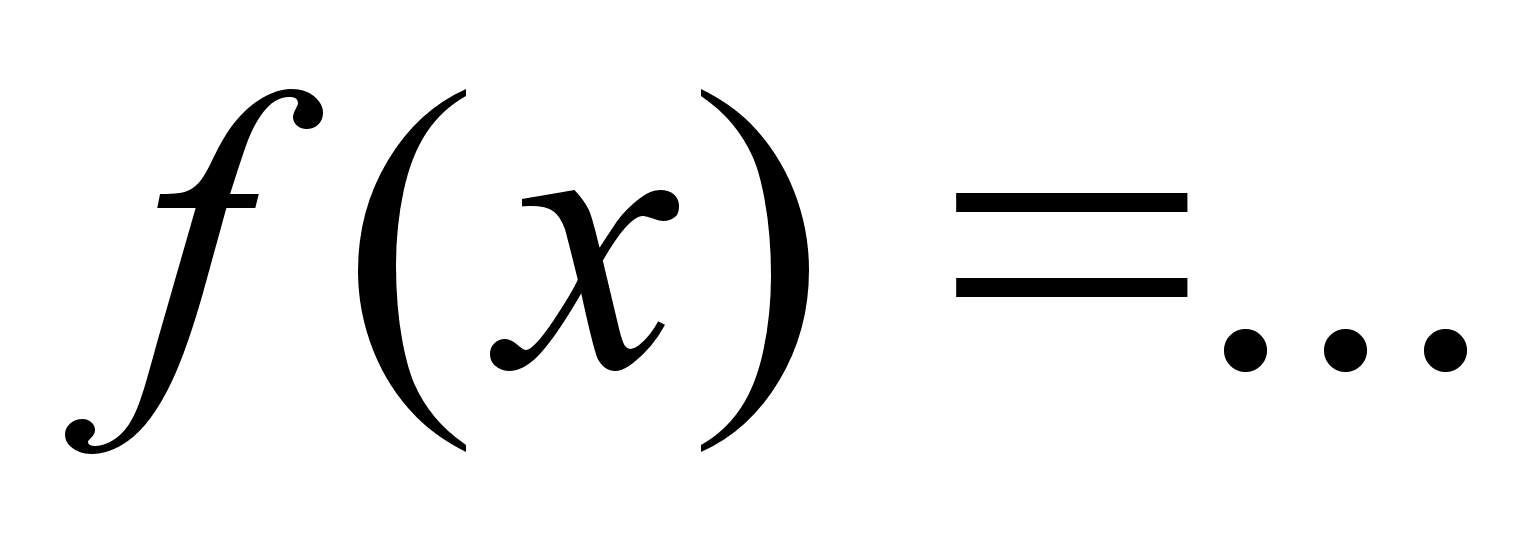 (варианты 1-30),
предварительно
исследовав
ее по следующему
плану:
(варианты 1-30),
предварительно
исследовав
ее по следующему
плану:
найти область определения функции
 (для этого можно
преобразовать
формулу, разложив
числитель и
знаменатель
на множители);
(для этого можно
преобразовать
формулу, разложив
числитель и
знаменатель
на множители);если есть точки разрыва, то выяснить, есть ли в них вертикальные асимптоты (для этого найти в этих точках пределы функции слева и справа);
найти наклонные или горизонтальные асимптоты (для этого преобразовать формулу функции, выделив целую часть из дроби);
проверить, не обладает ли функция частными свойствами: а) четностью или нечетностью, б) периодичностью (если нет, то доказать, пояснить это);
найти точки пересечения графика с осями координат и интервалы знакопостоянства, если точки пересечения с осью
 легко находятся;
легко находятся;найти производную и критические точки;
по знаку производной выяснить интервалы возрастания и убывания функции и что она имеет в критических точках;
изобразить систему координат (в соответствии с исследованными свойствами) и отметить в ней все найденные точки, изобразить асимптоты; для уточнения вида графика найти координаты нескольких дополнительных точек; отметить их и нарисовать график;
если в п.5 не были найдены точки пересечения графика с осью
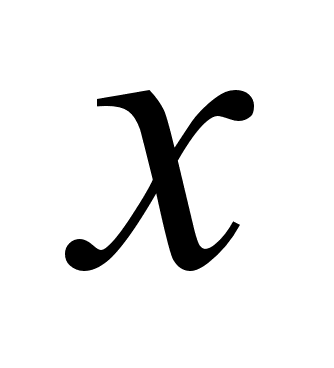 (нули функции),
то найти их
теперь по графику;
(нули функции),
то найти их
теперь по графику;найти область изменения функции (по графику и исследованным свойствам).
Варианты:
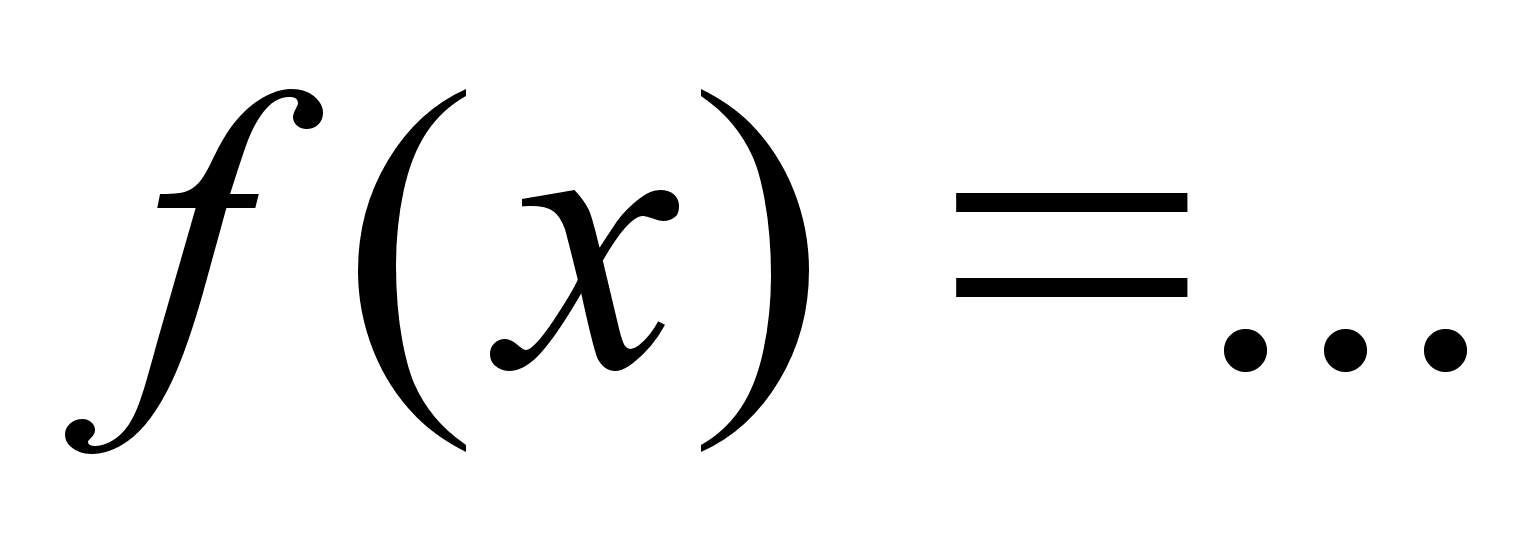
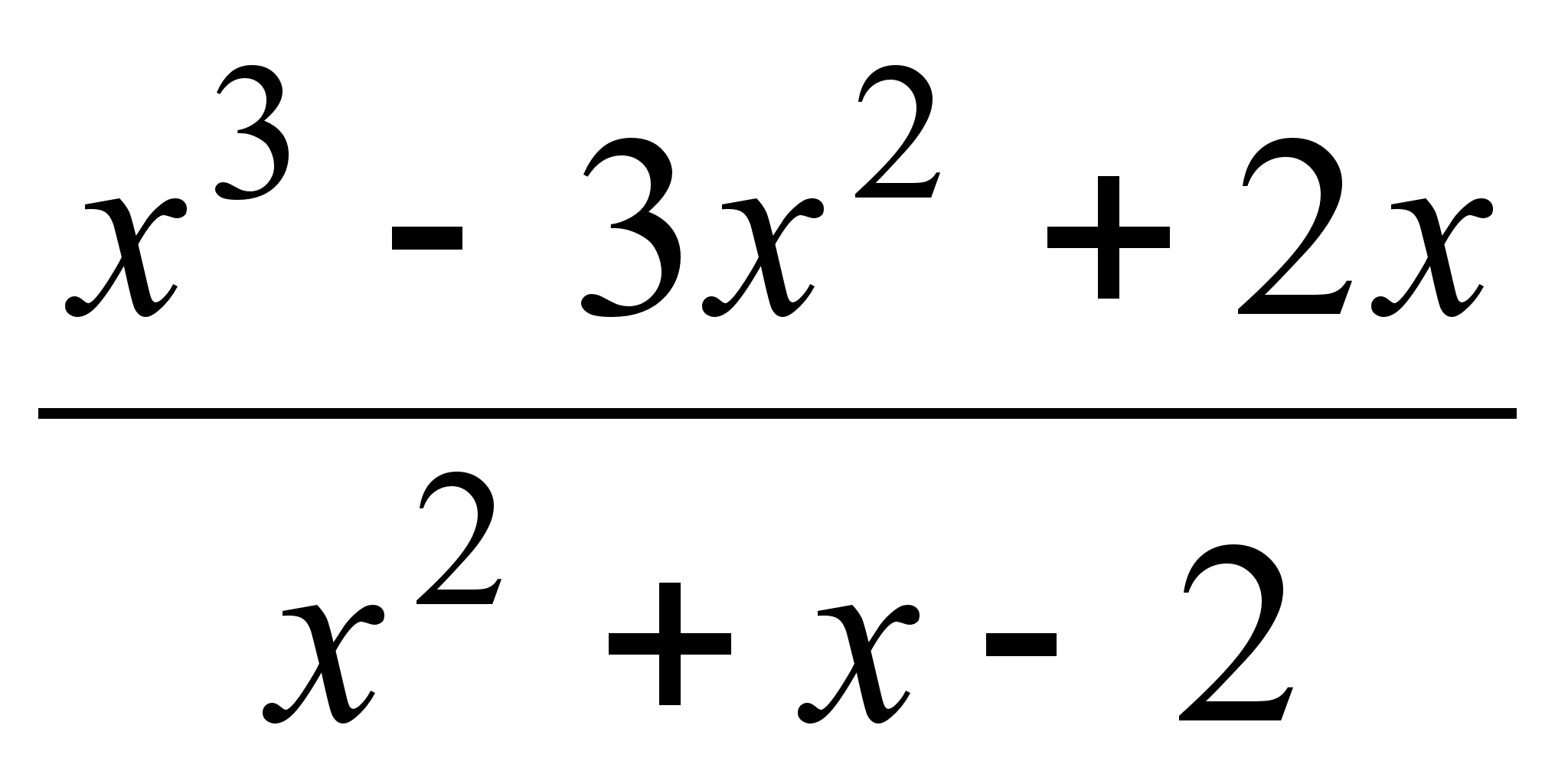 ;
11)
;
11)
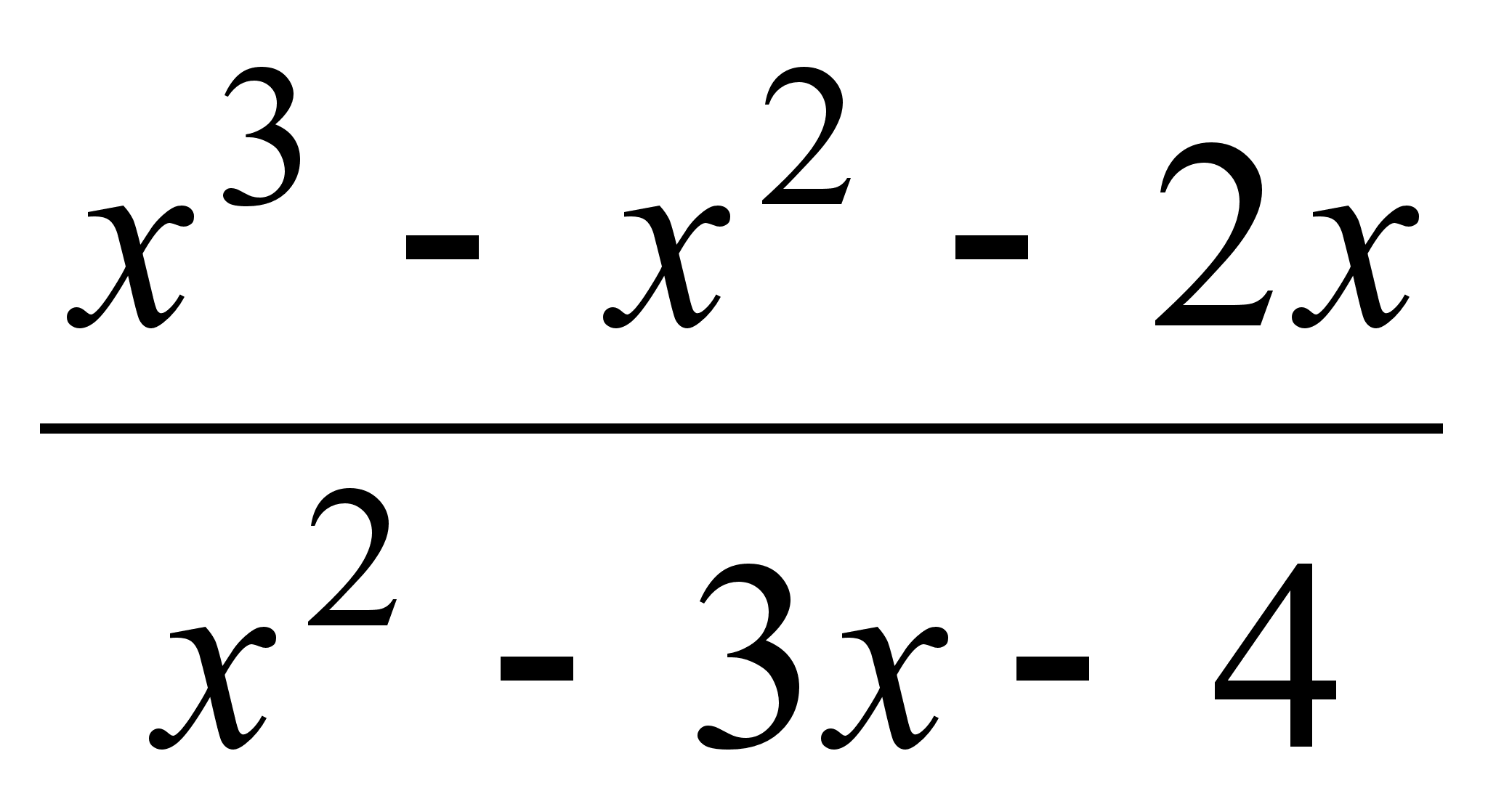 ;
21)
;
21)
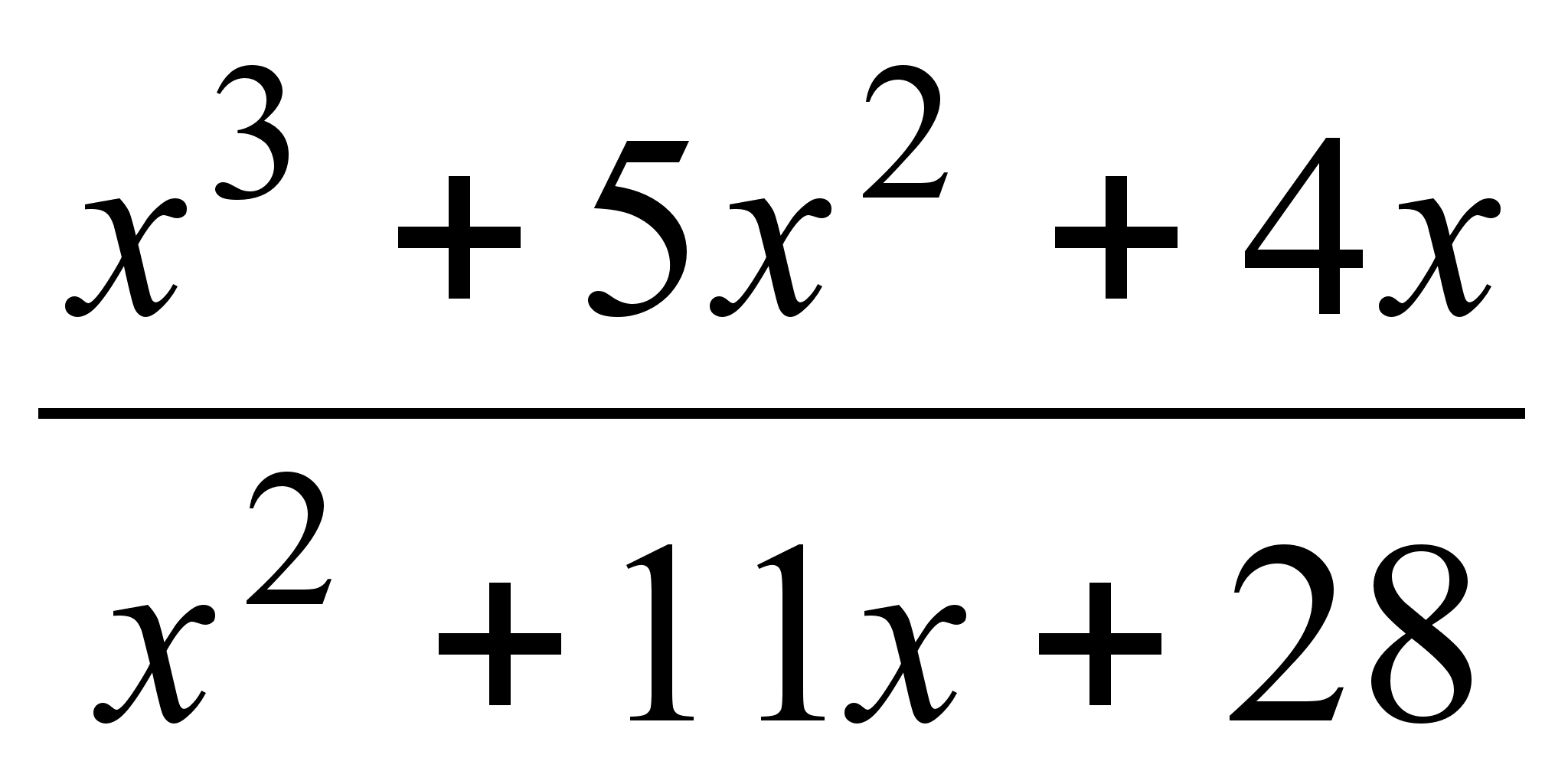 ;
;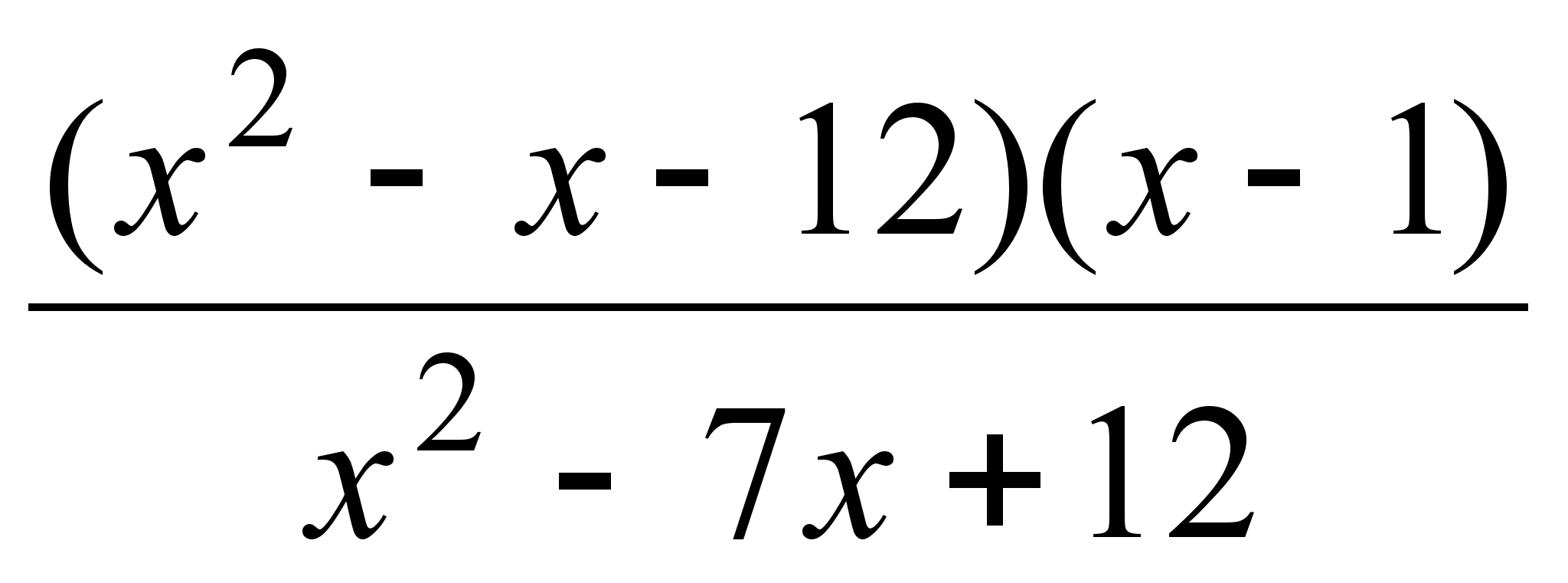 ;
12)
;
12)
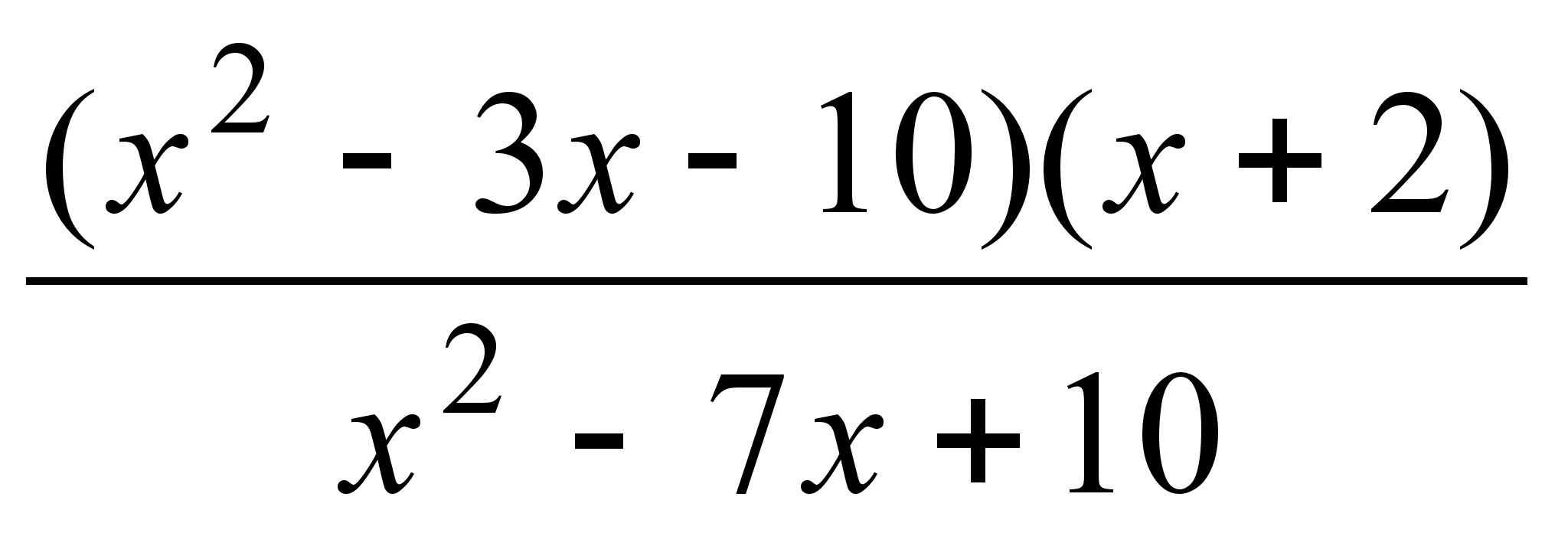 ;
22)
;
22)
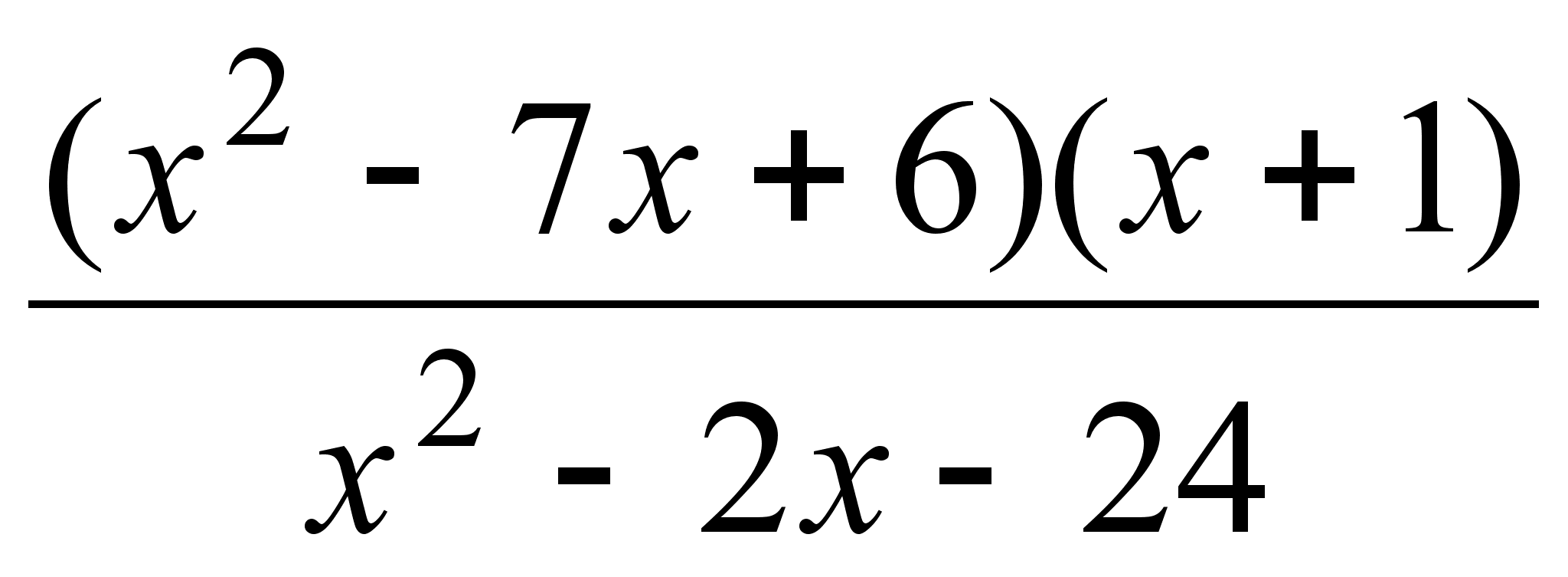 ;
;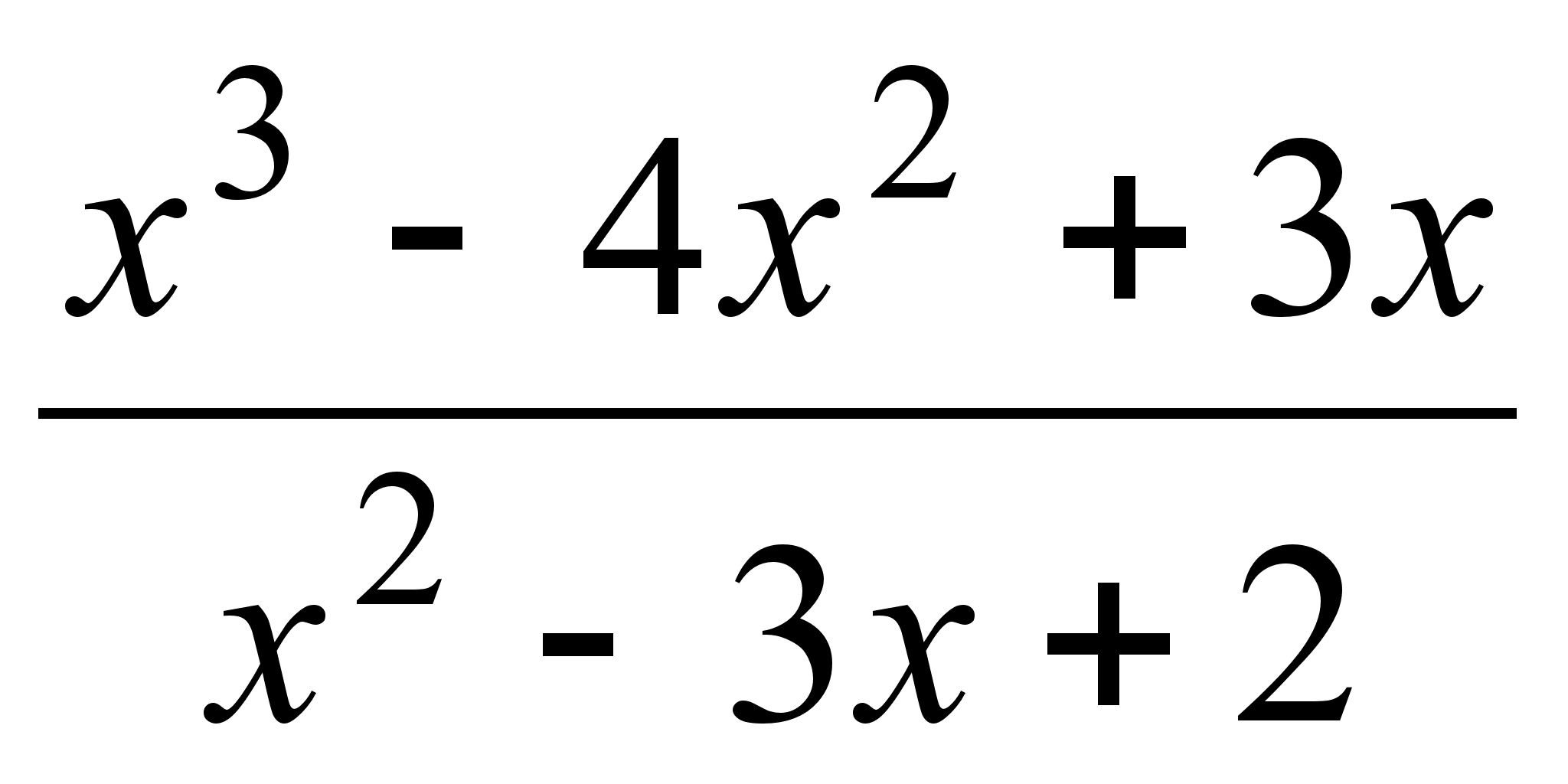 ;
13)
;
13)
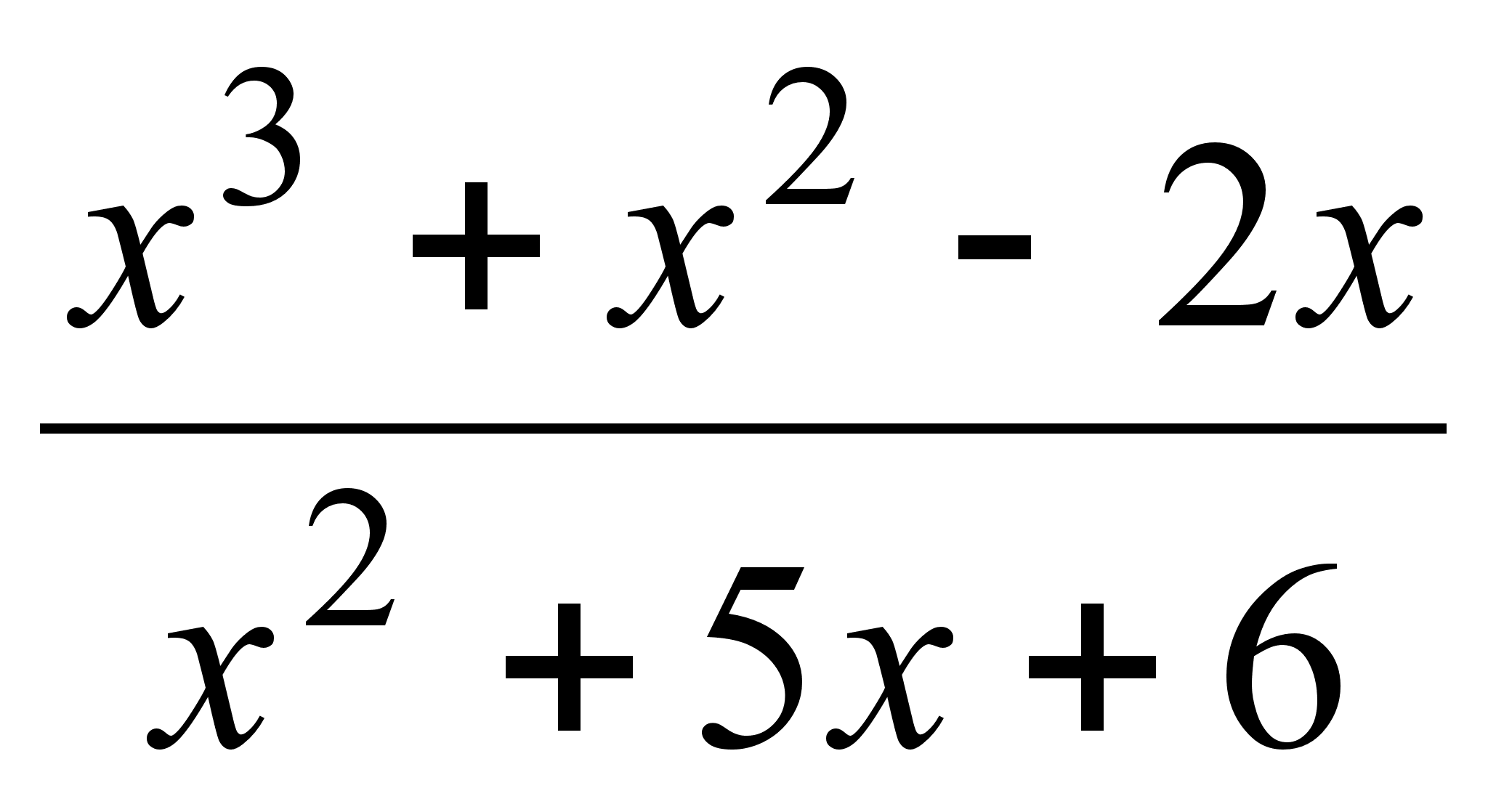 ;
23)
;
23)
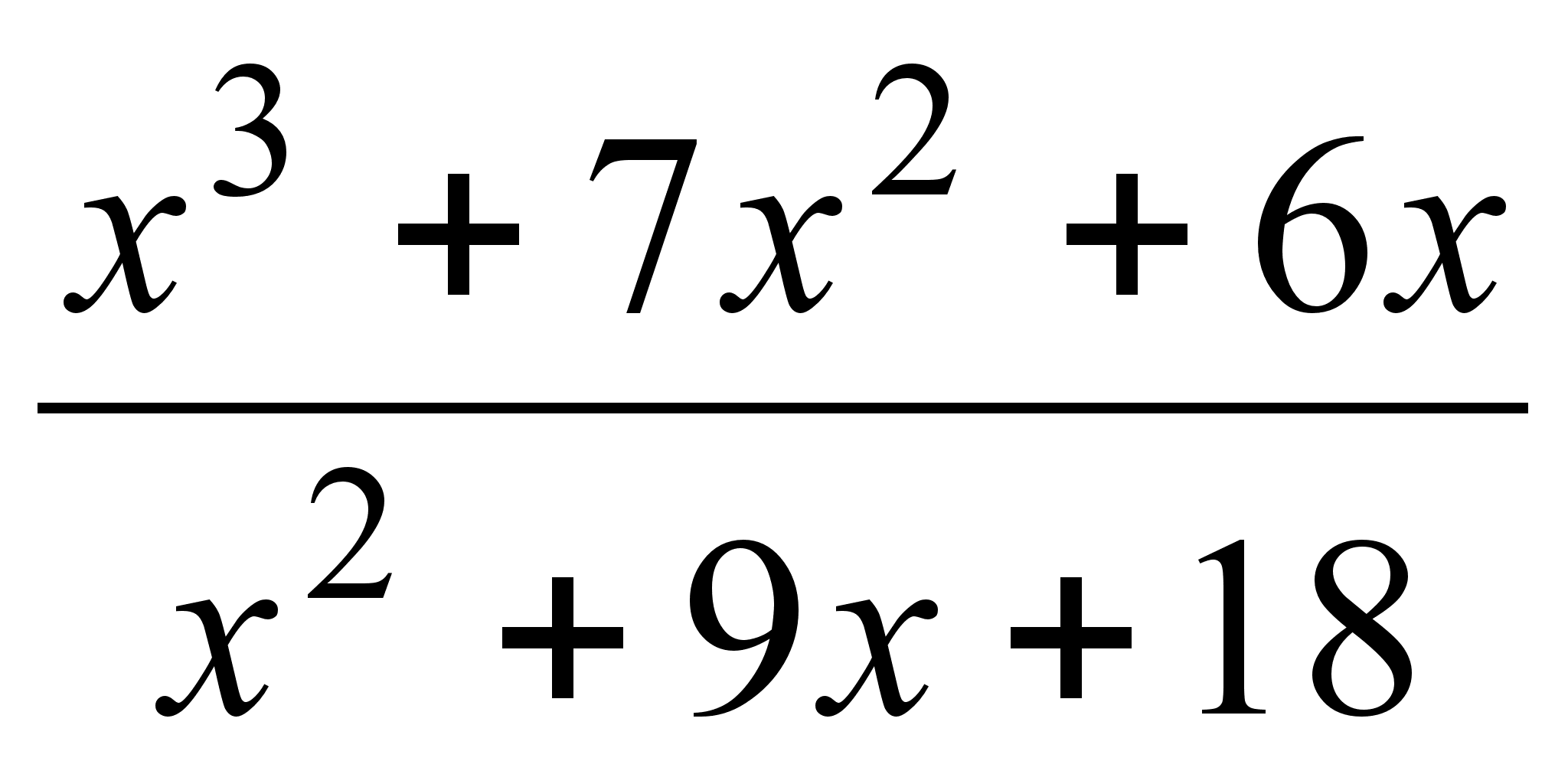 ;
;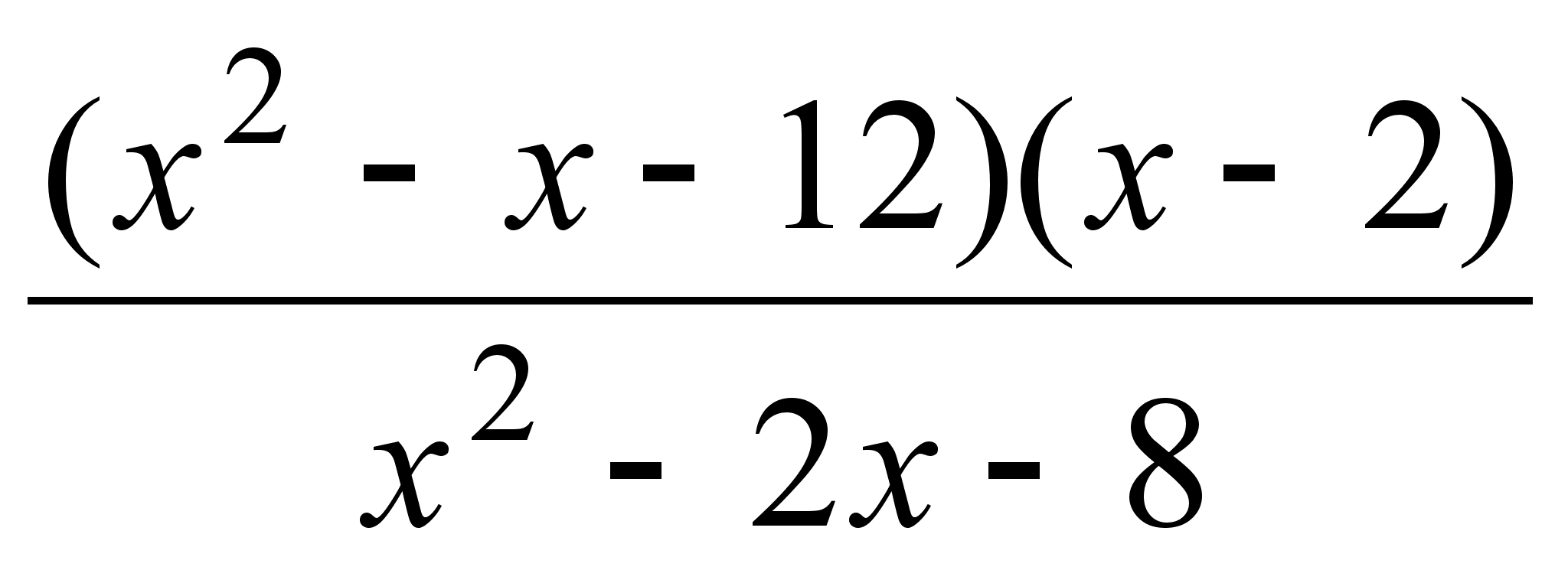 ;
14)
;
14)
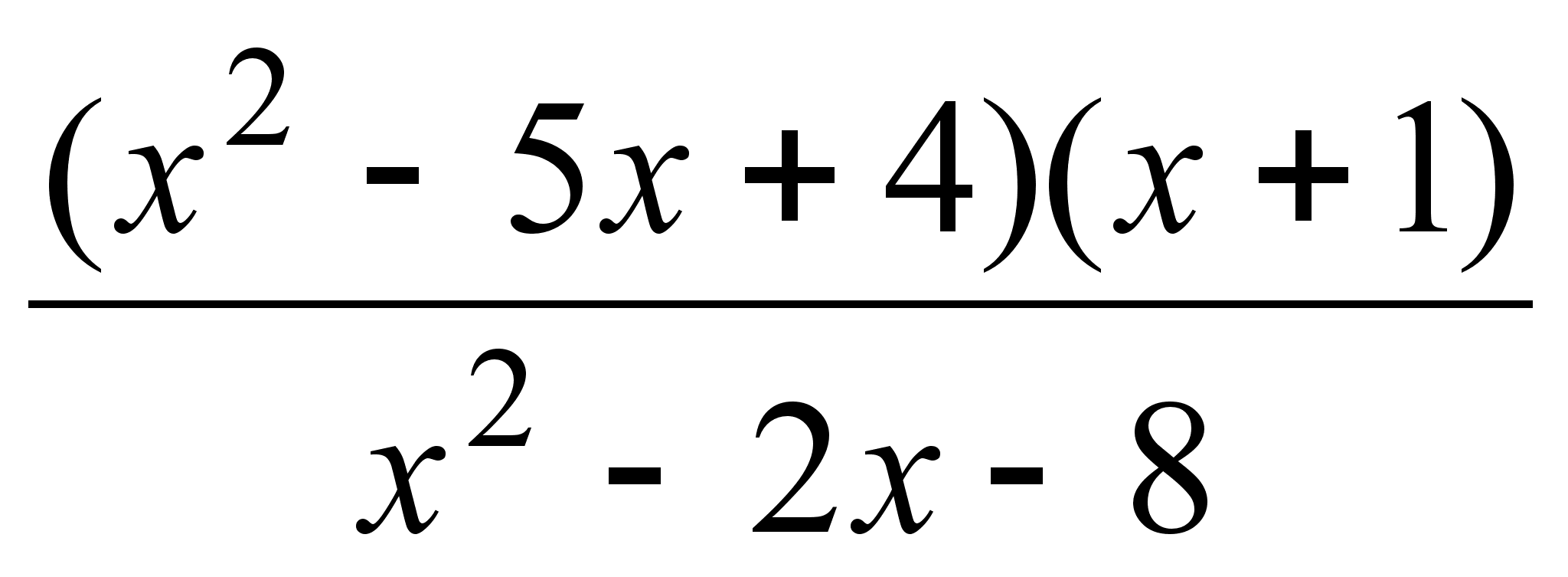 ;
24)
;
24)
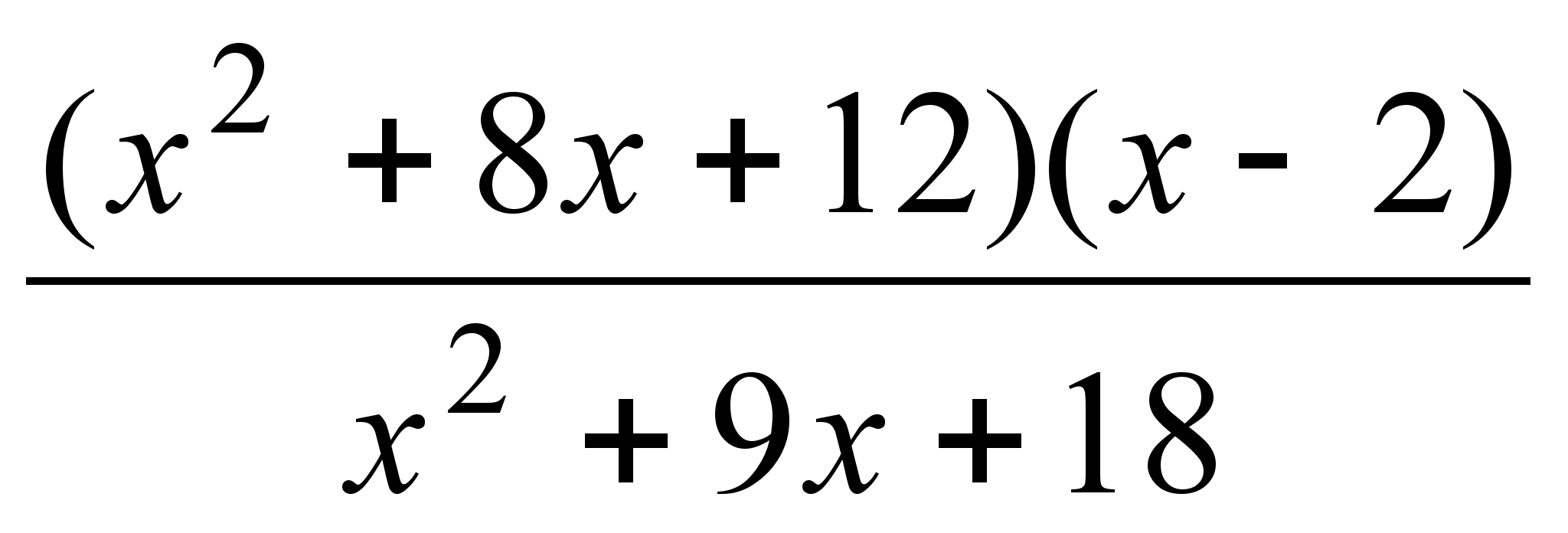 ;
;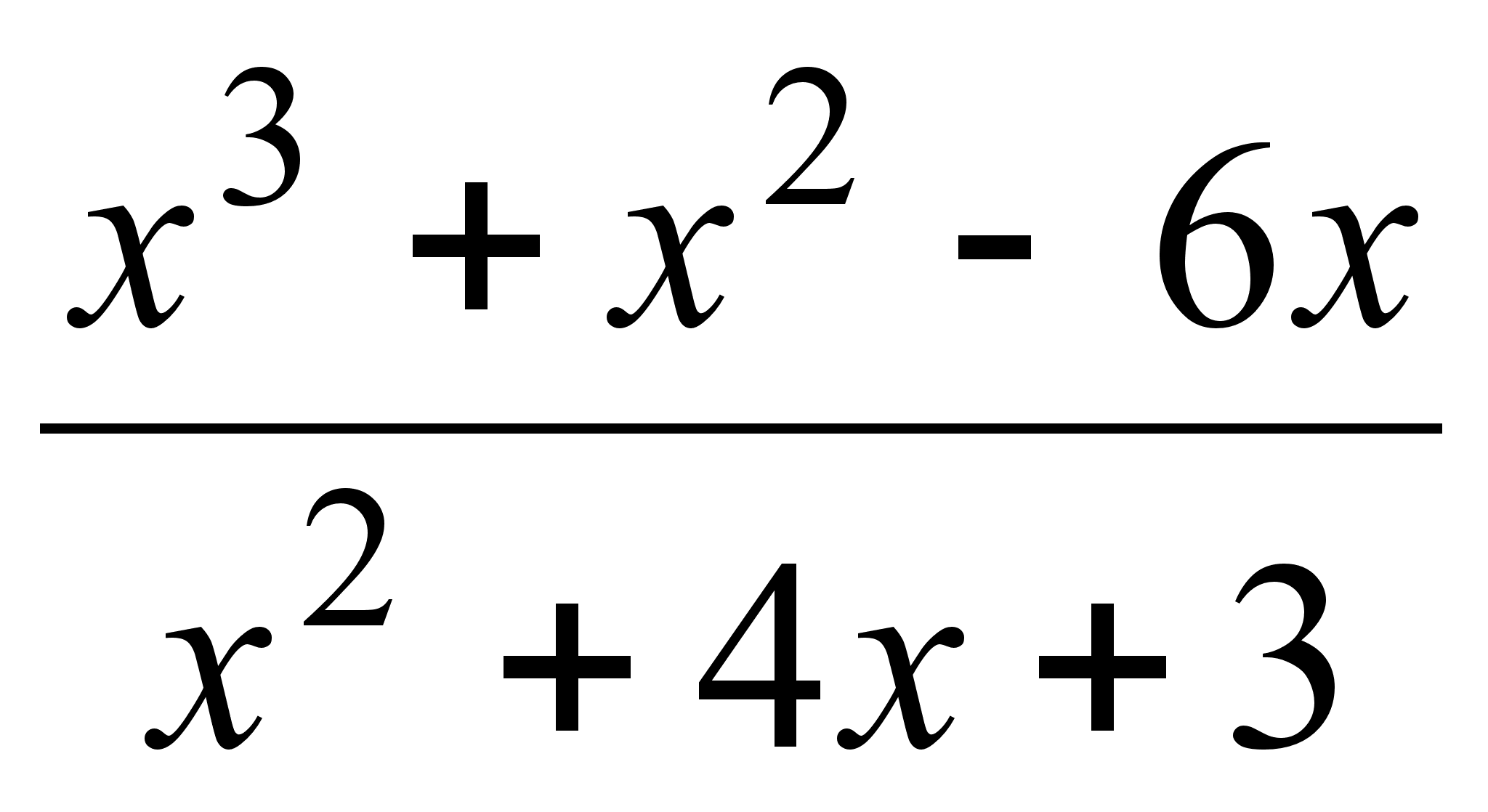 ;
15)
;
15)
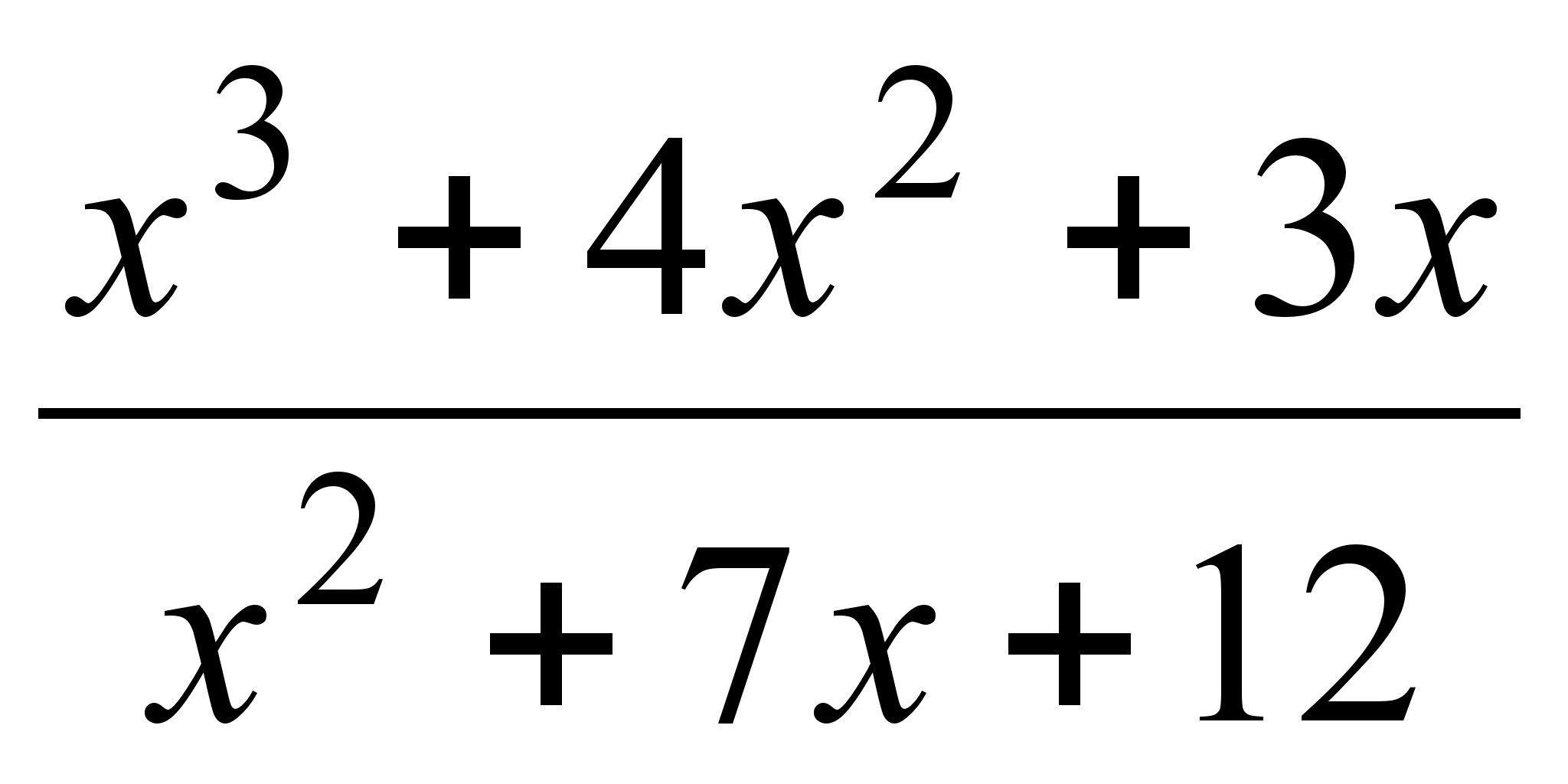 ;
25)
;
25)
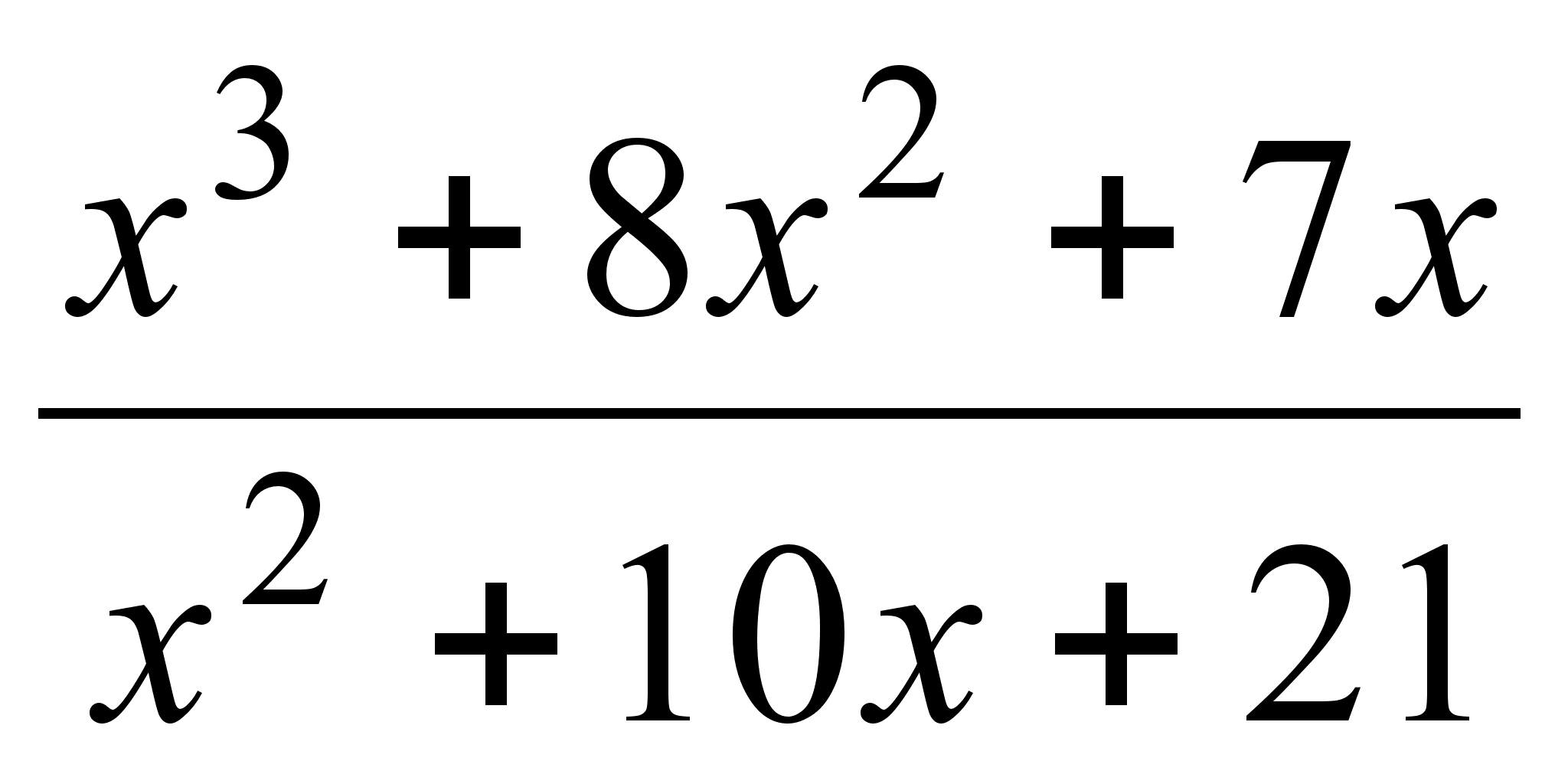 ;
;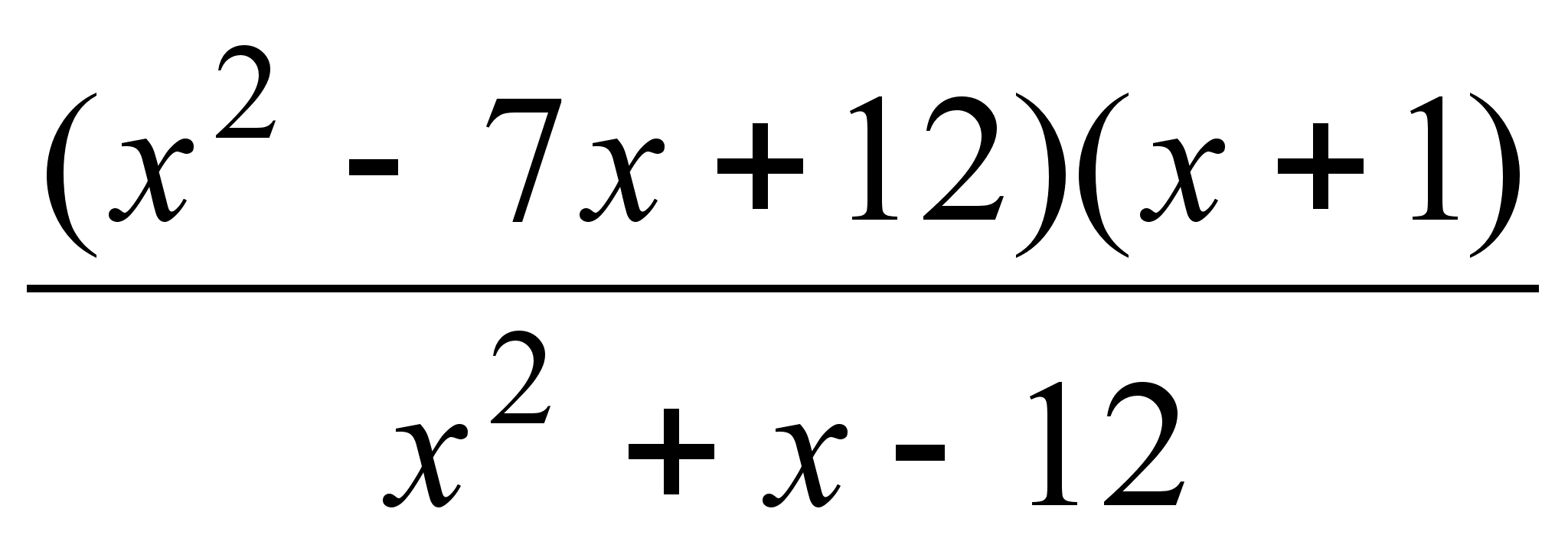 ;
16)
;
16)
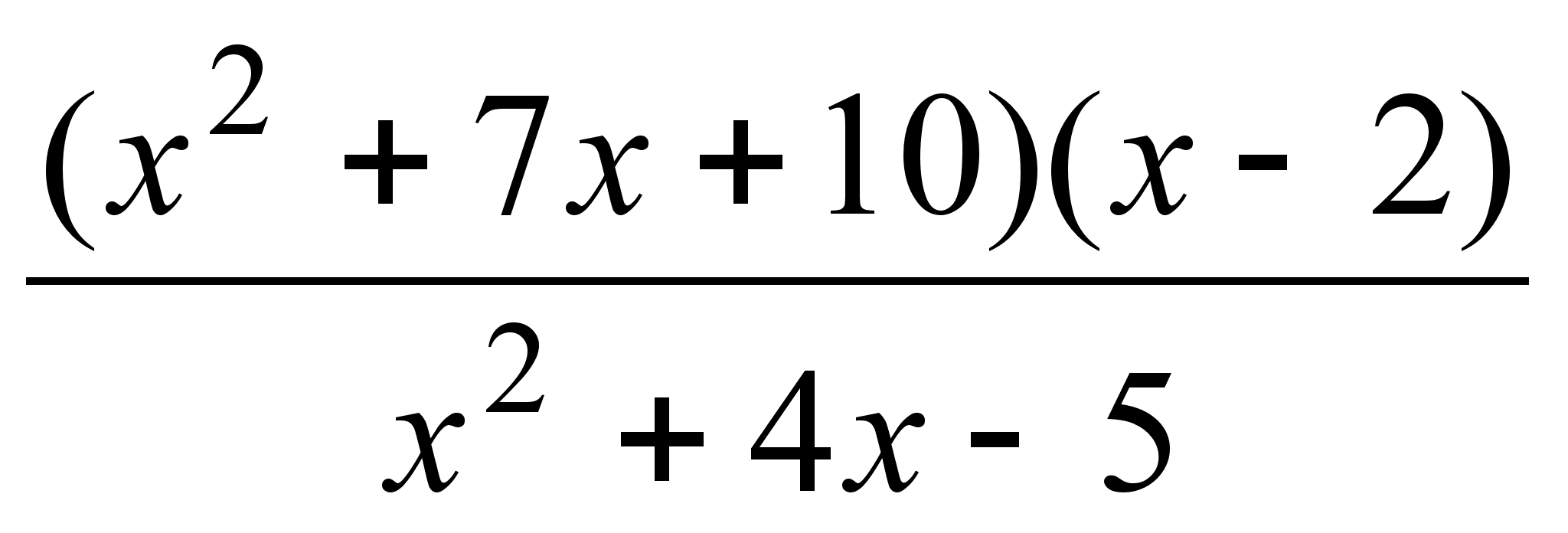 ;
26)
;
26)
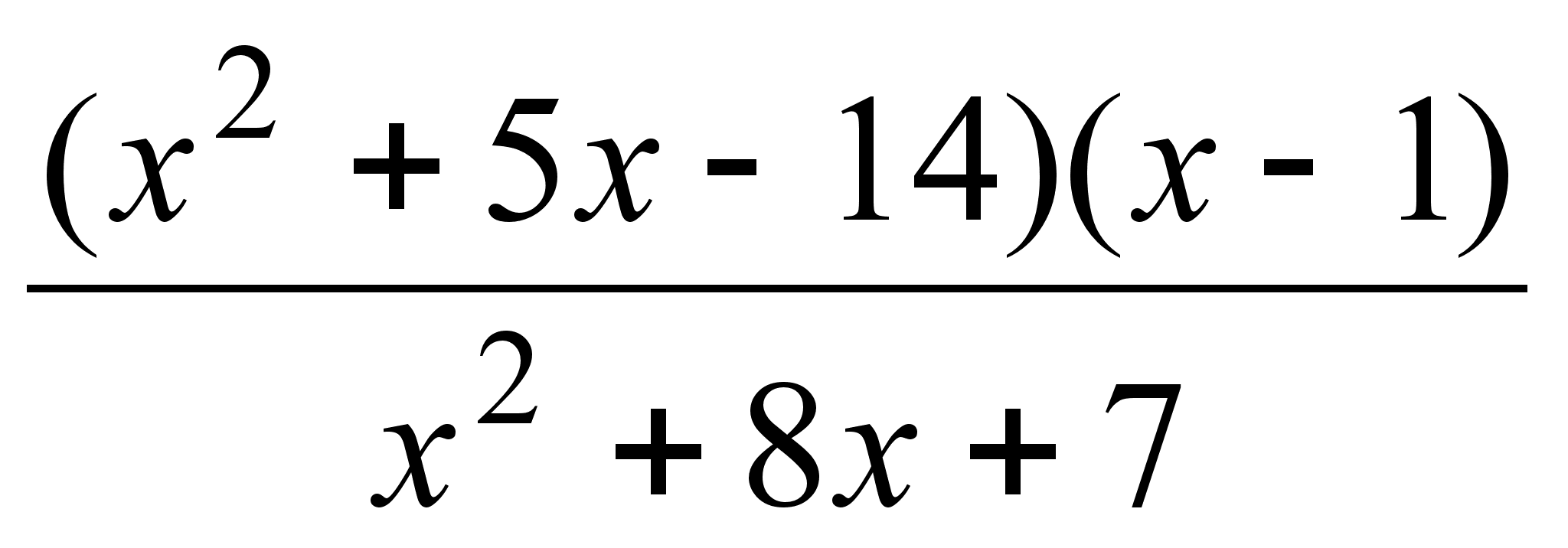 ;
;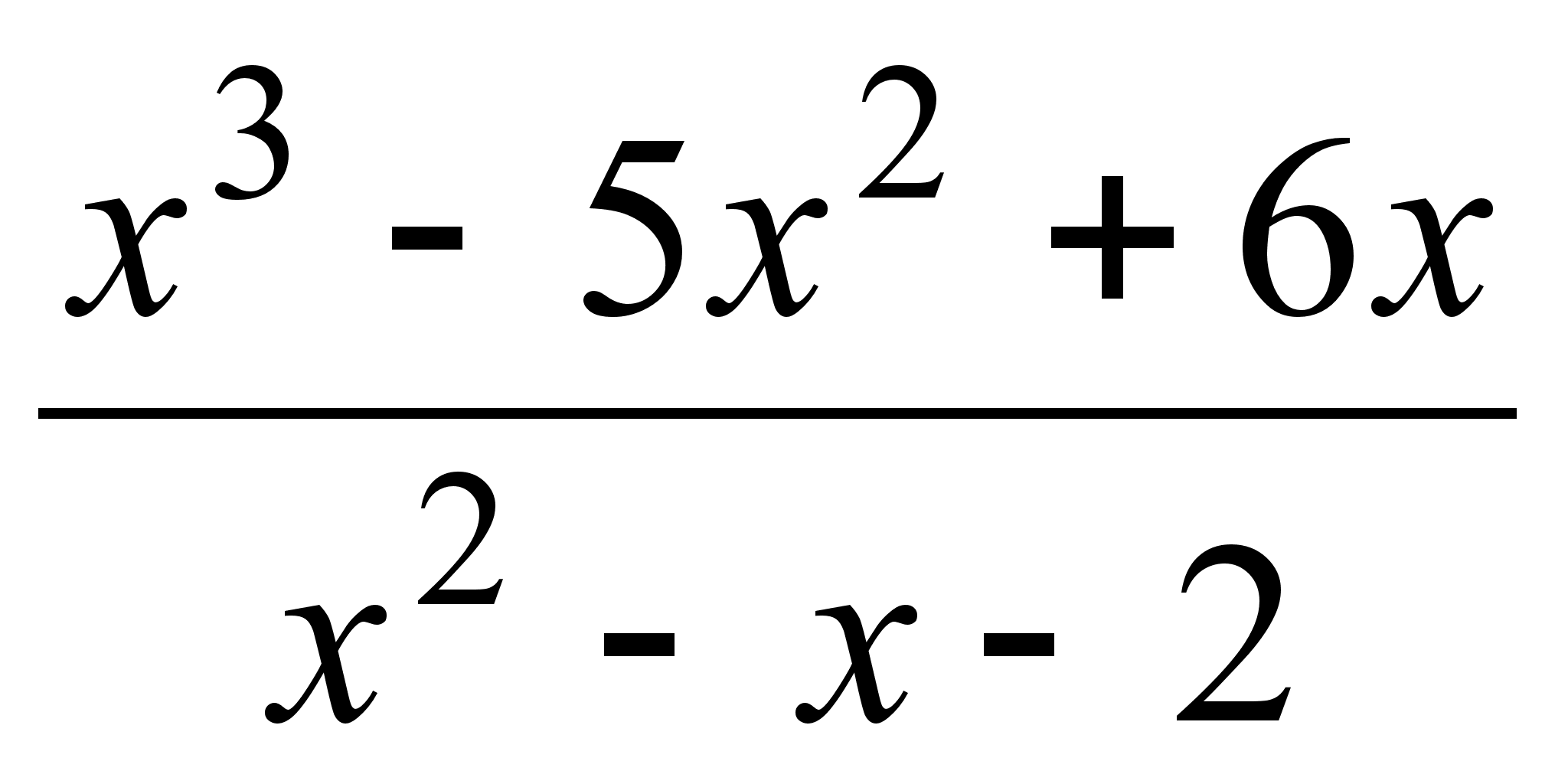 ;
17)
;
17)
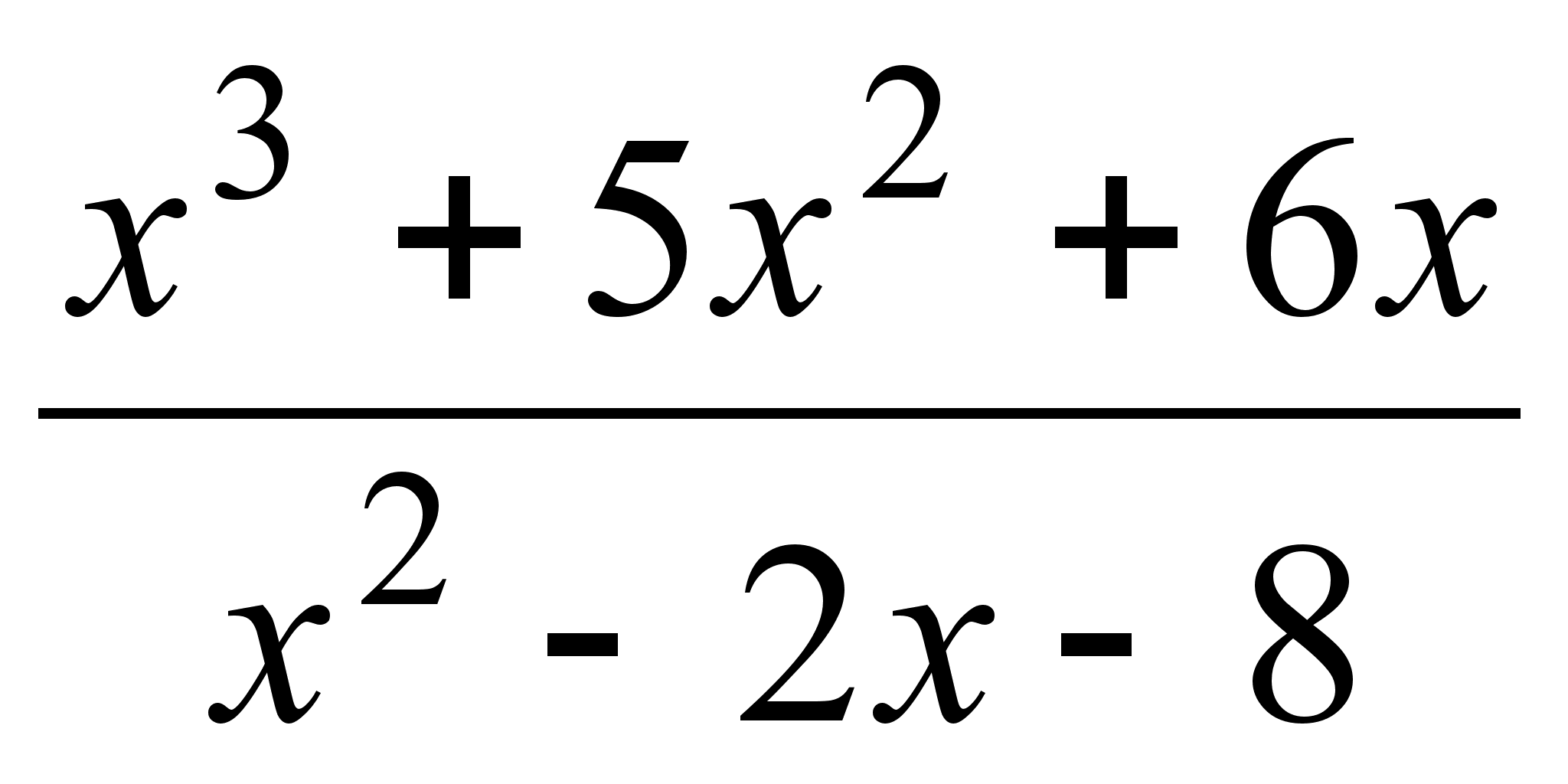 ;
27)
;
27)
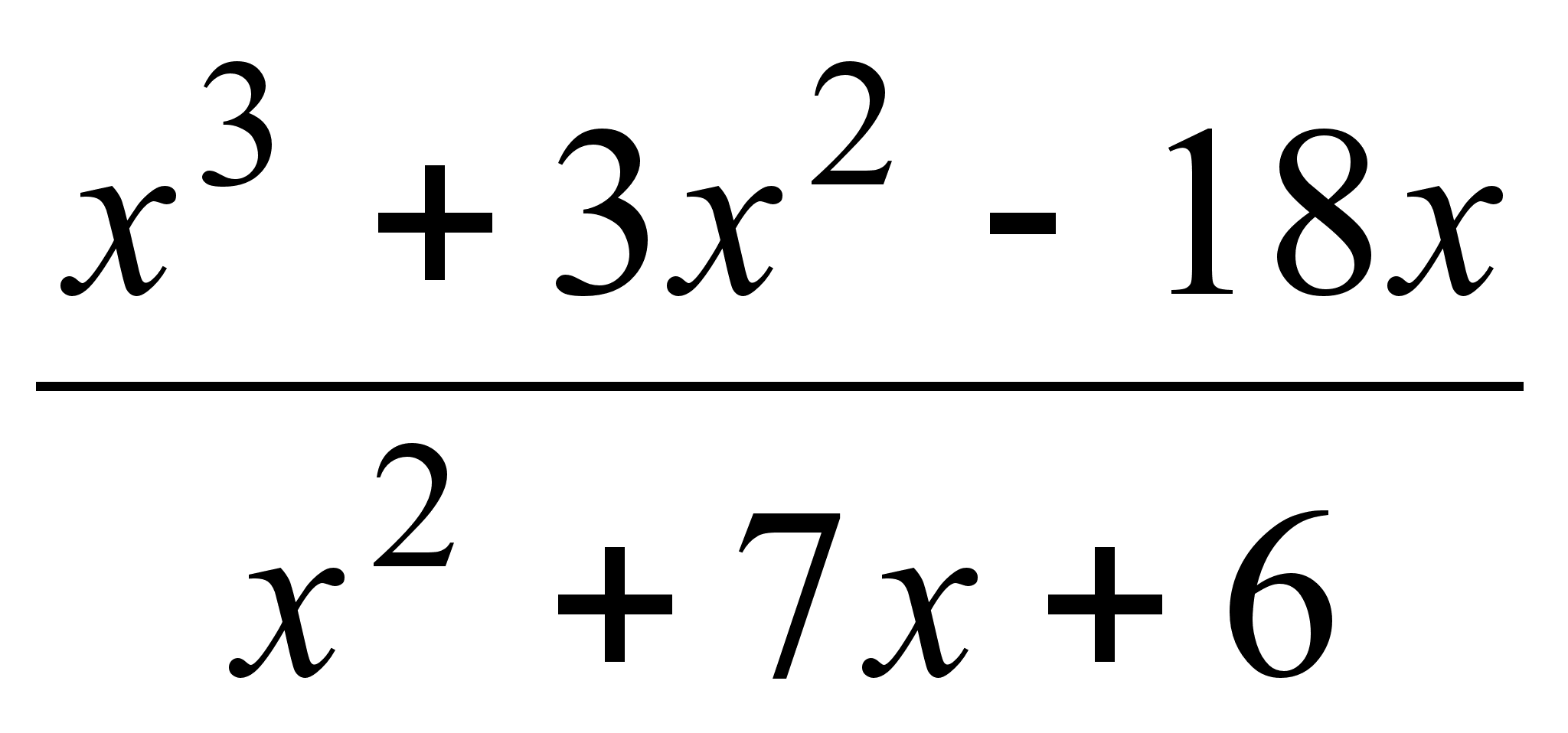 ;
;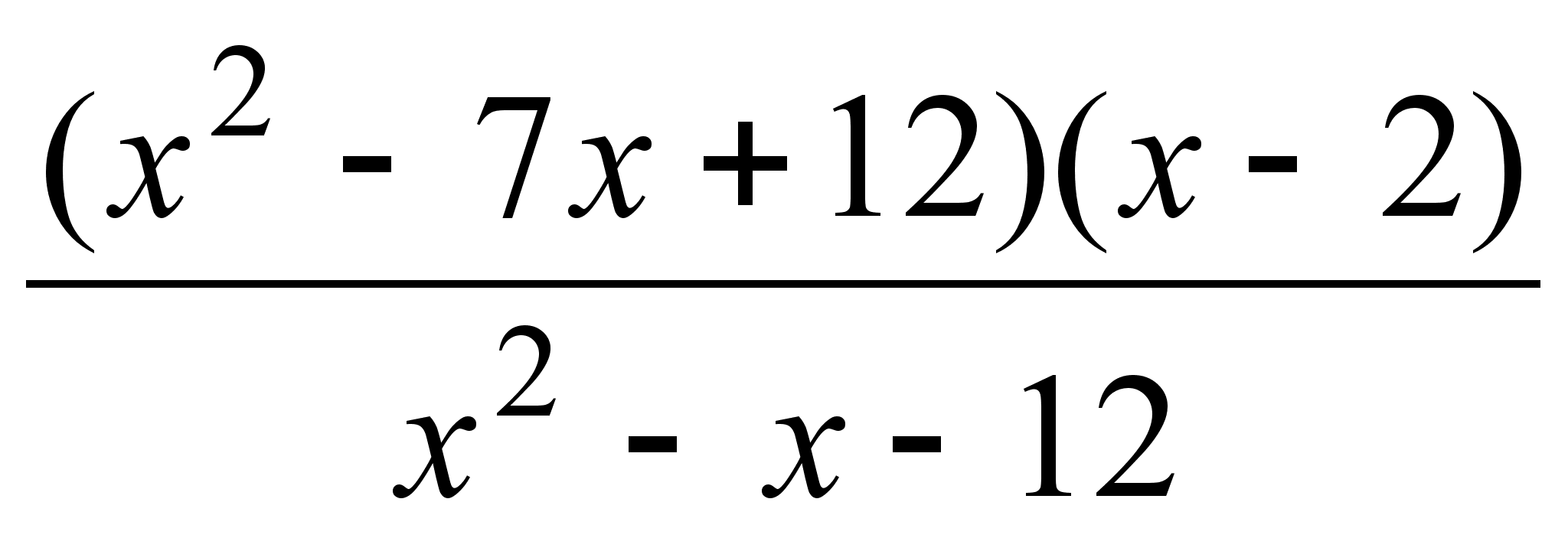 ;
18)
;
18)
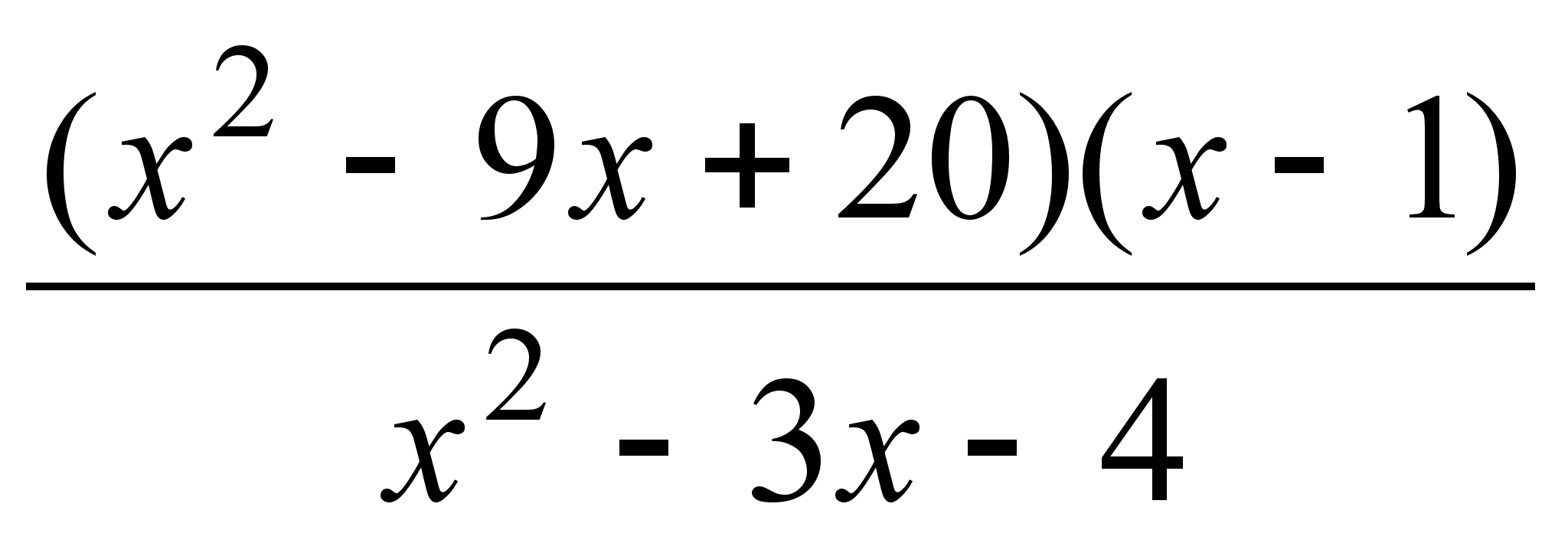 ;
28)
;
28)
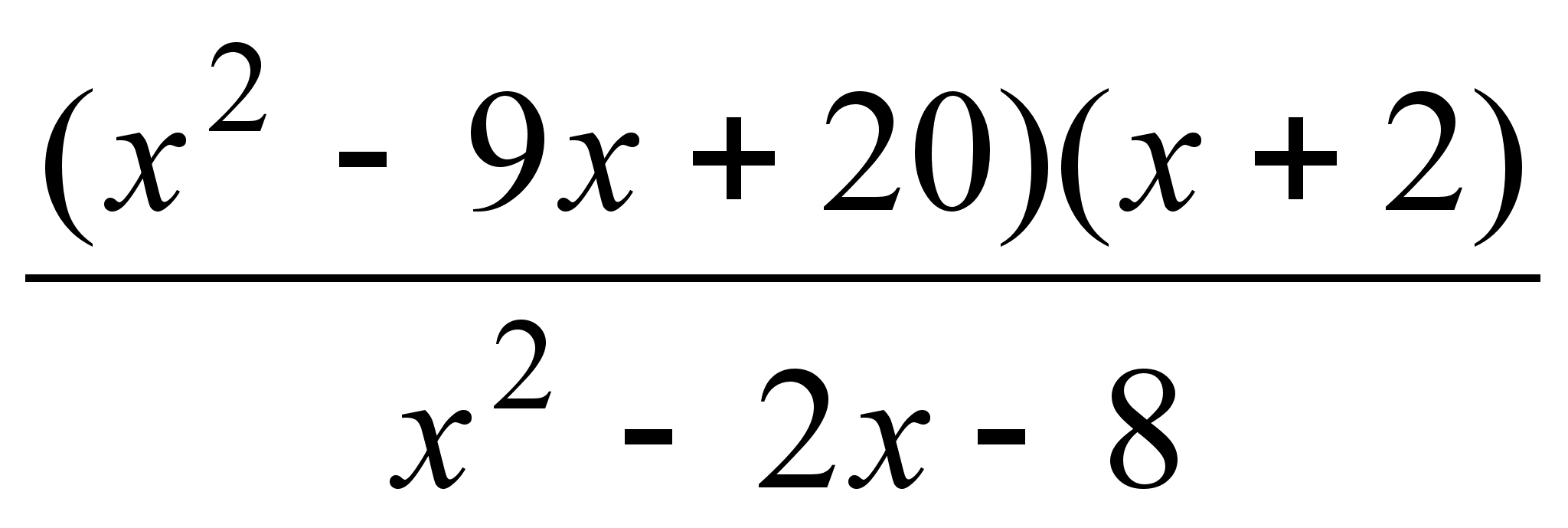 ;
;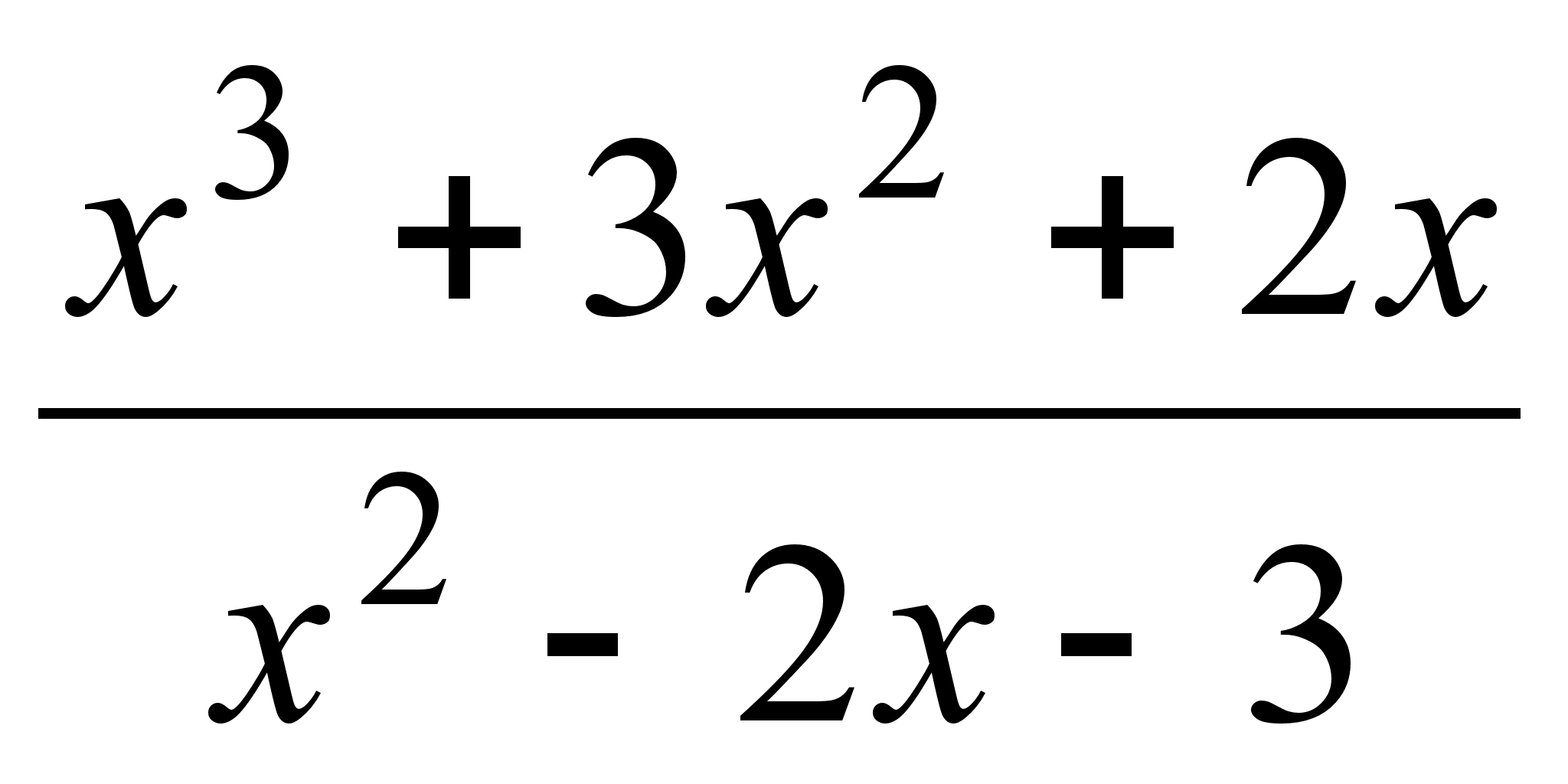 ;
19)
;
19)
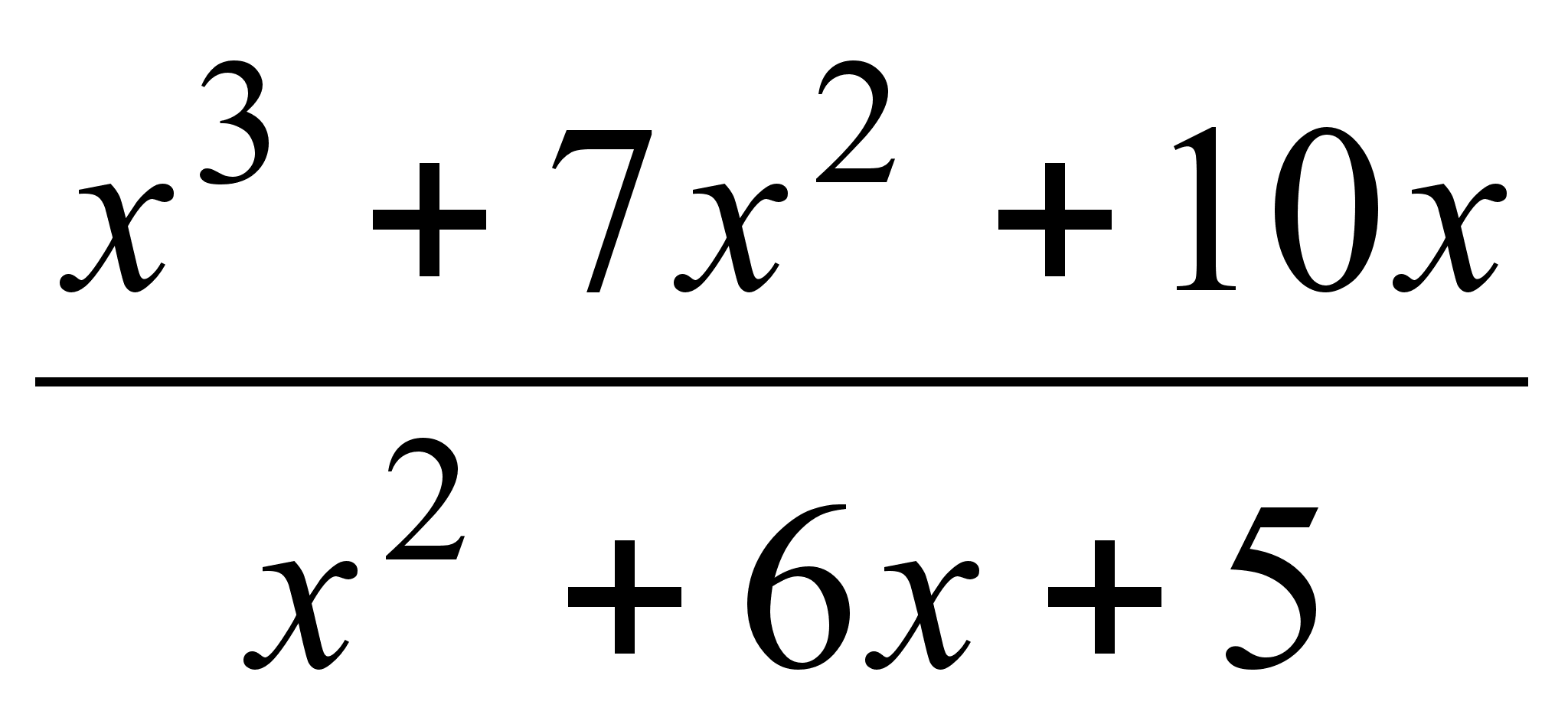 ;
29)
;
29)
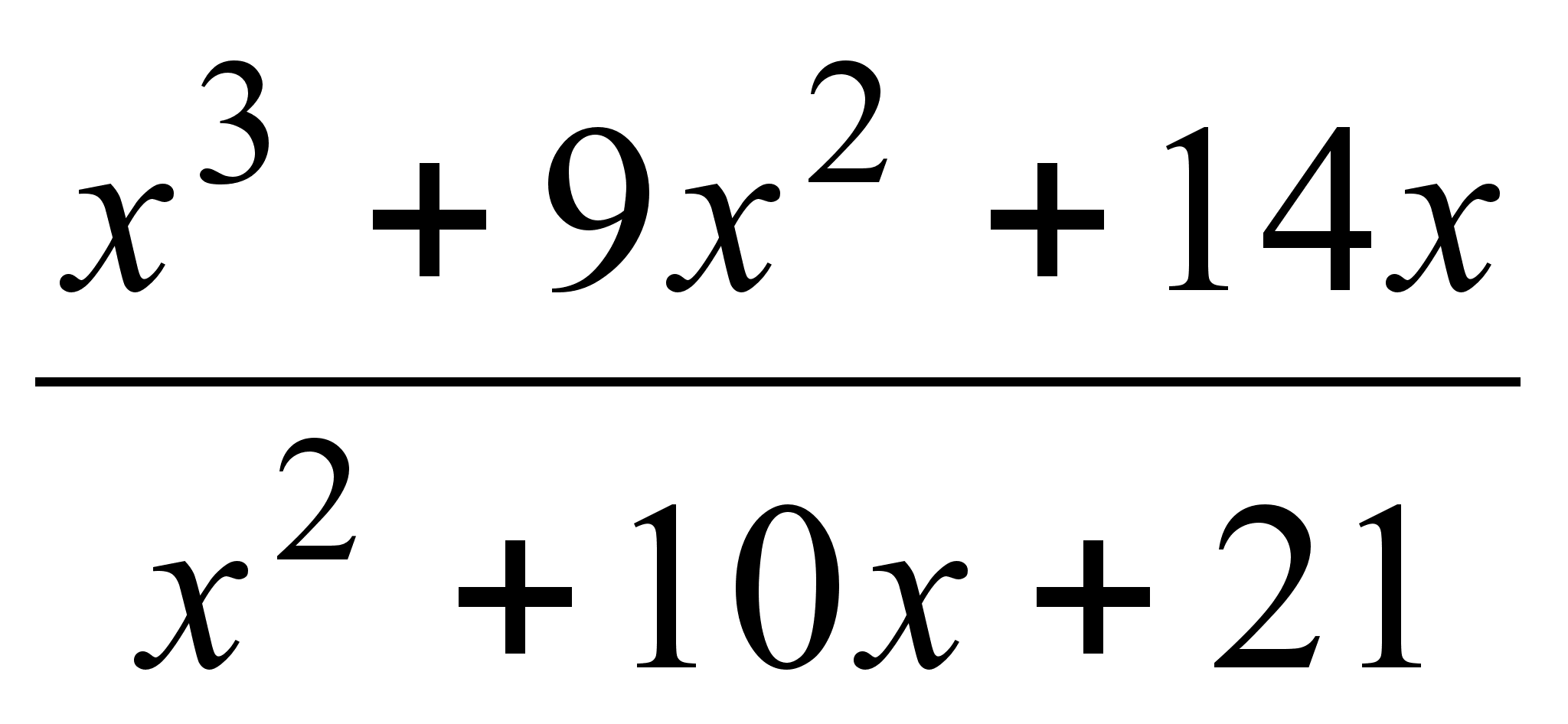 ;
;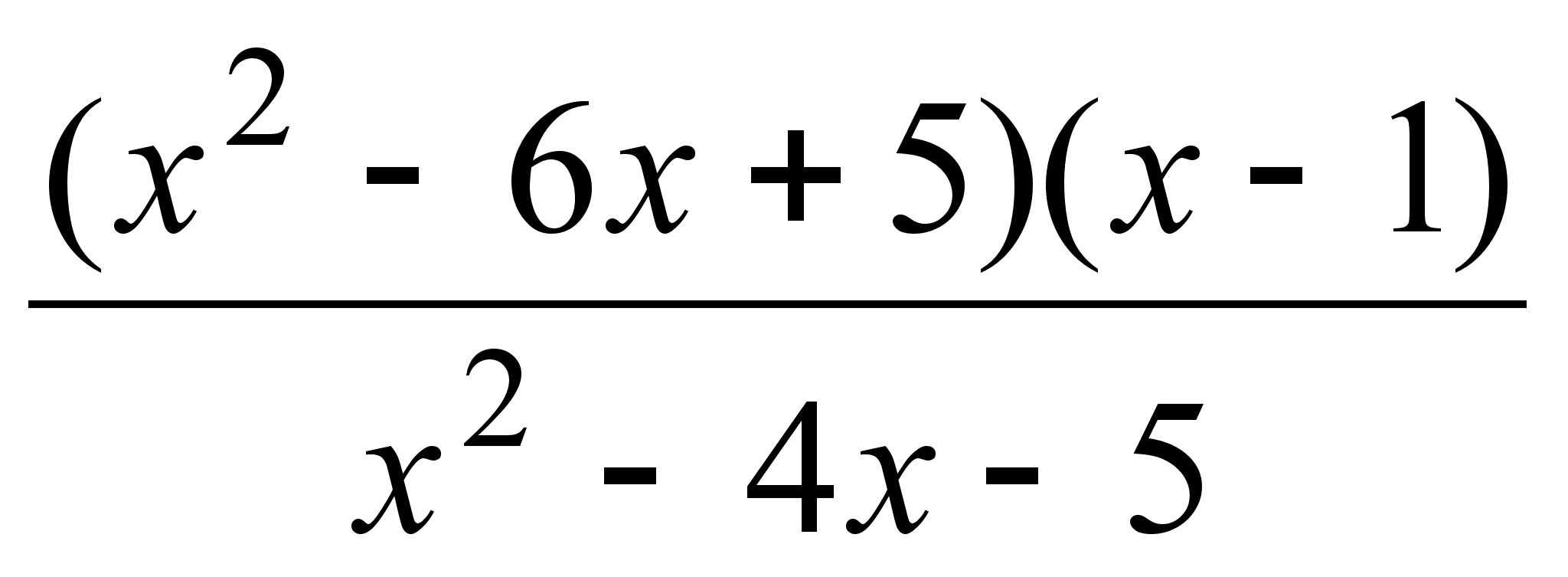 ;
20)
;
20)
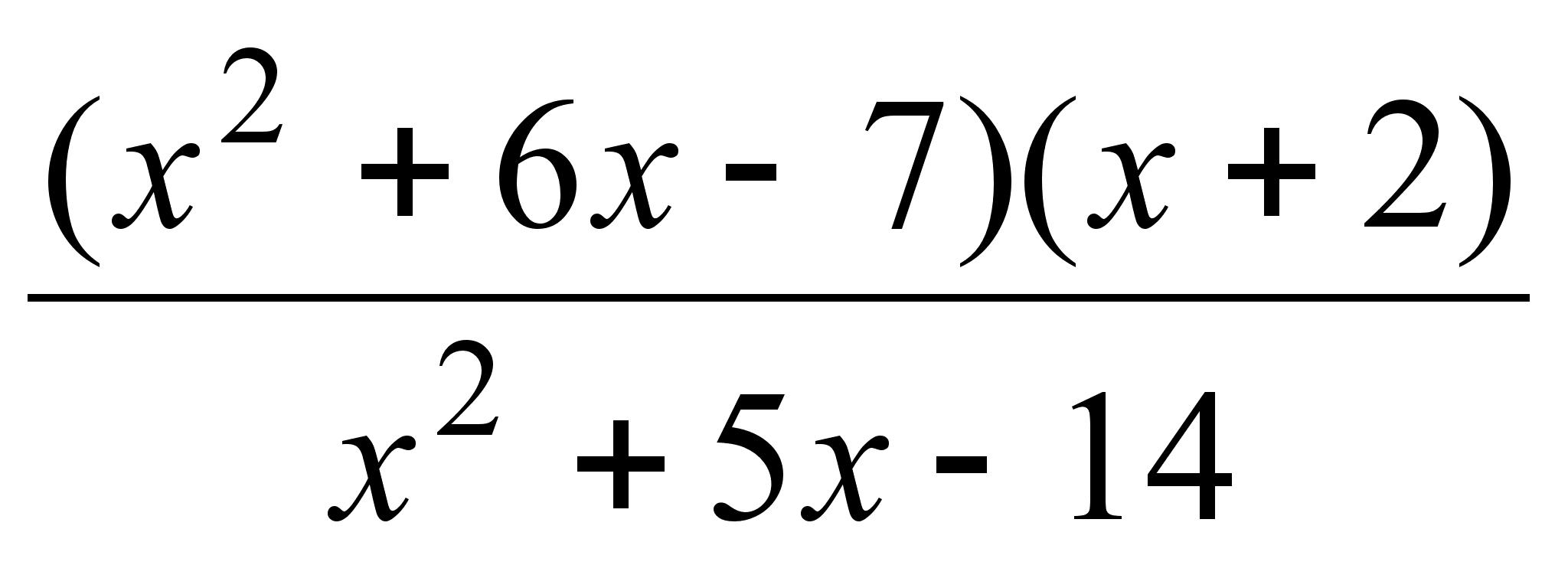 ;
30)
;
30)
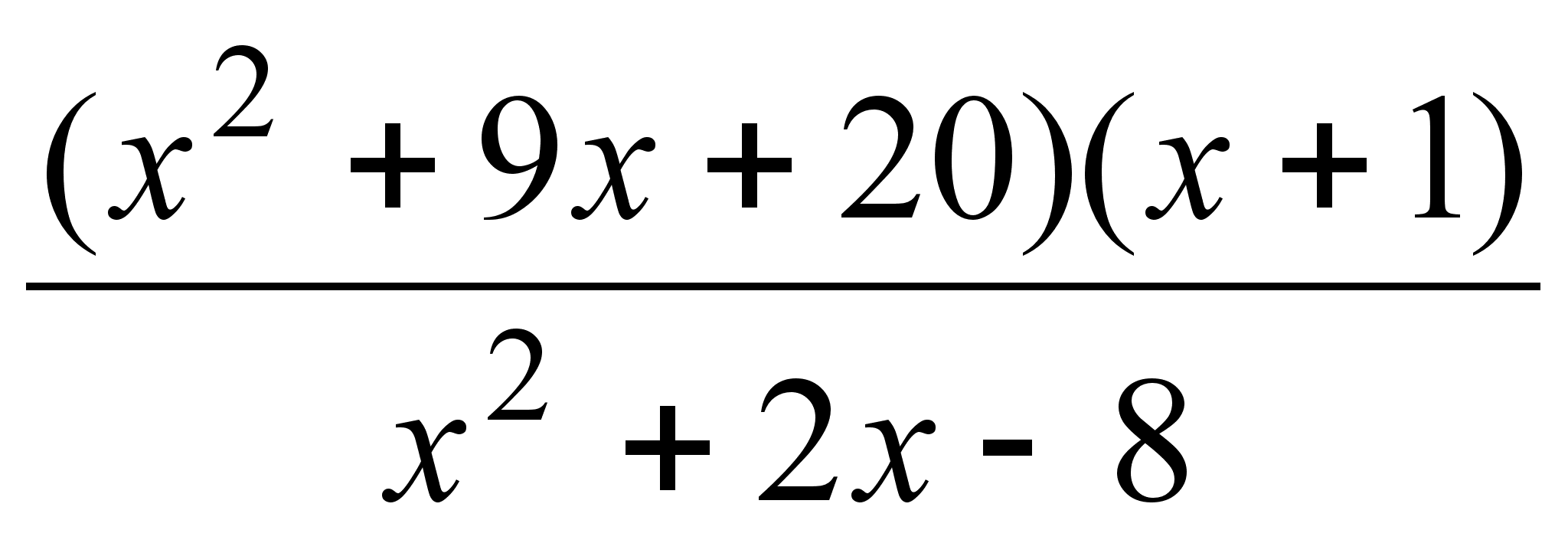 .
.
Пример.
Исследовать
функцию
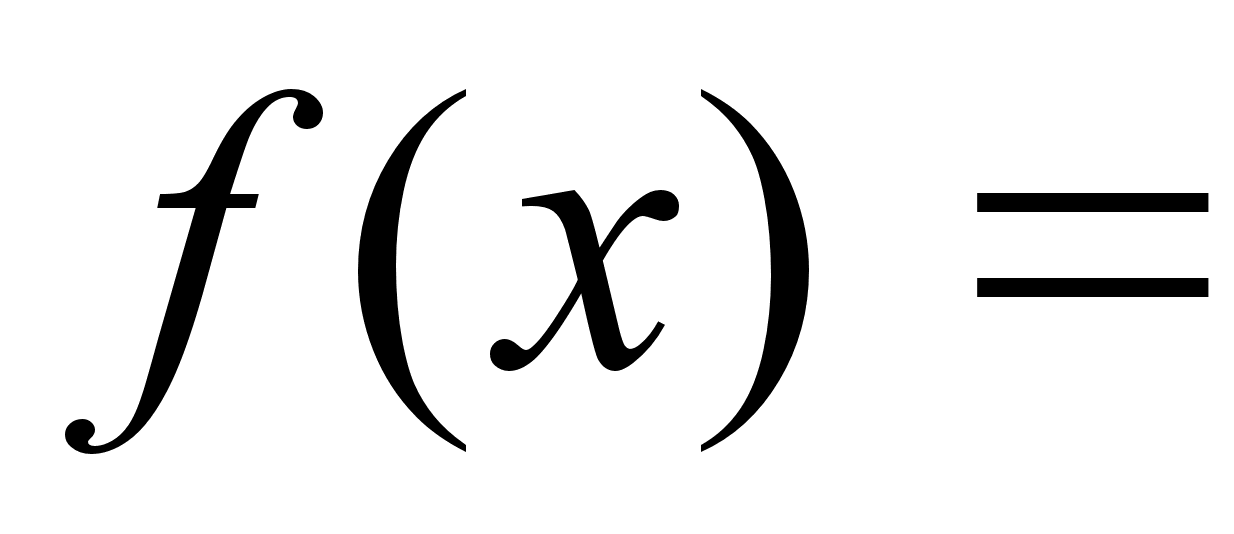
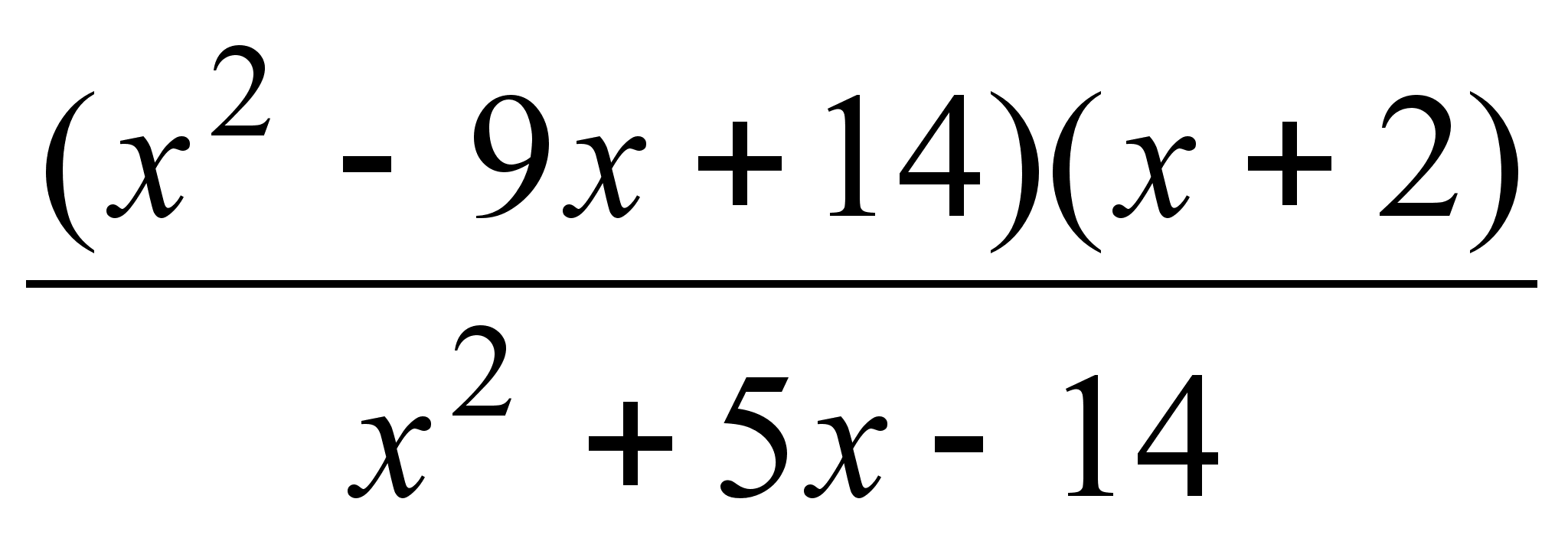 .
.
Решение.
1)
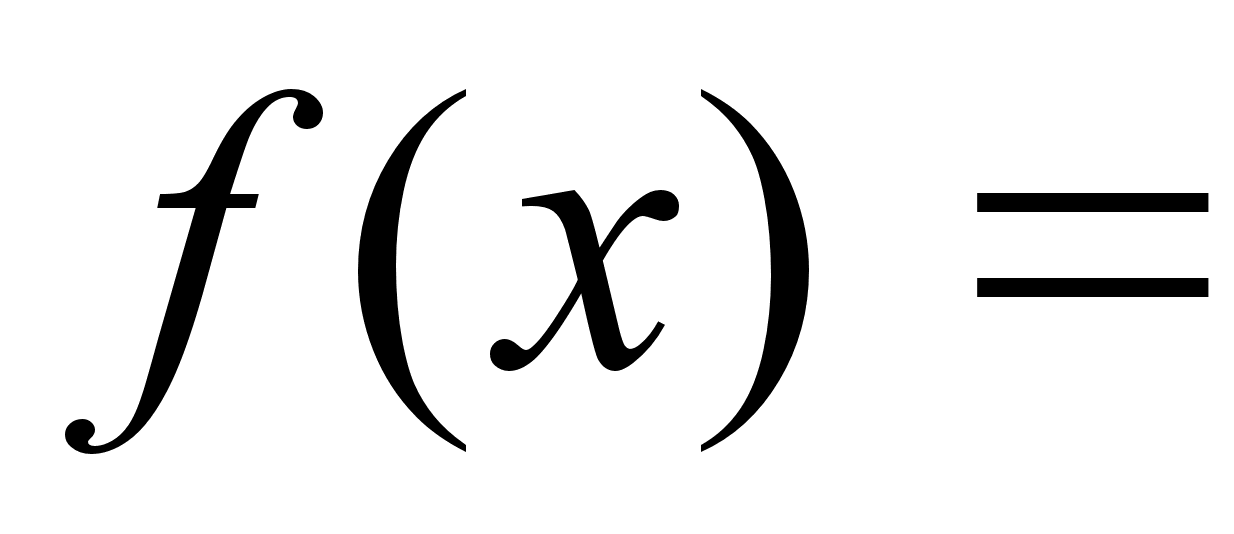
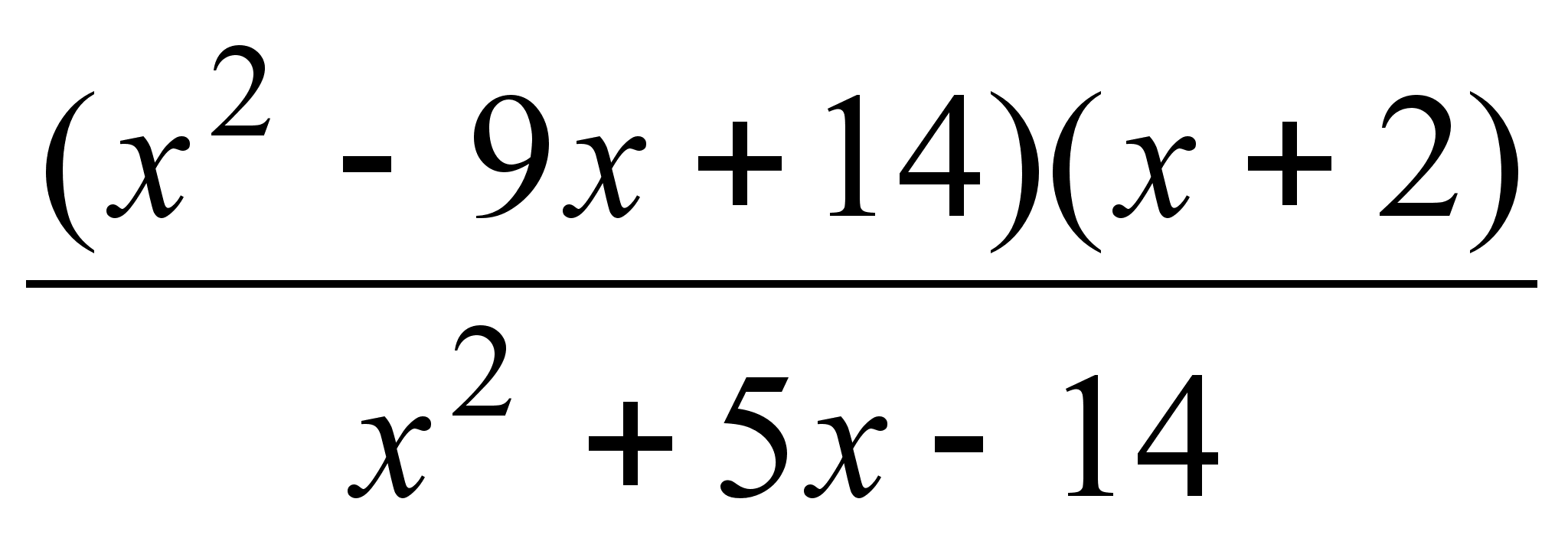 =
=
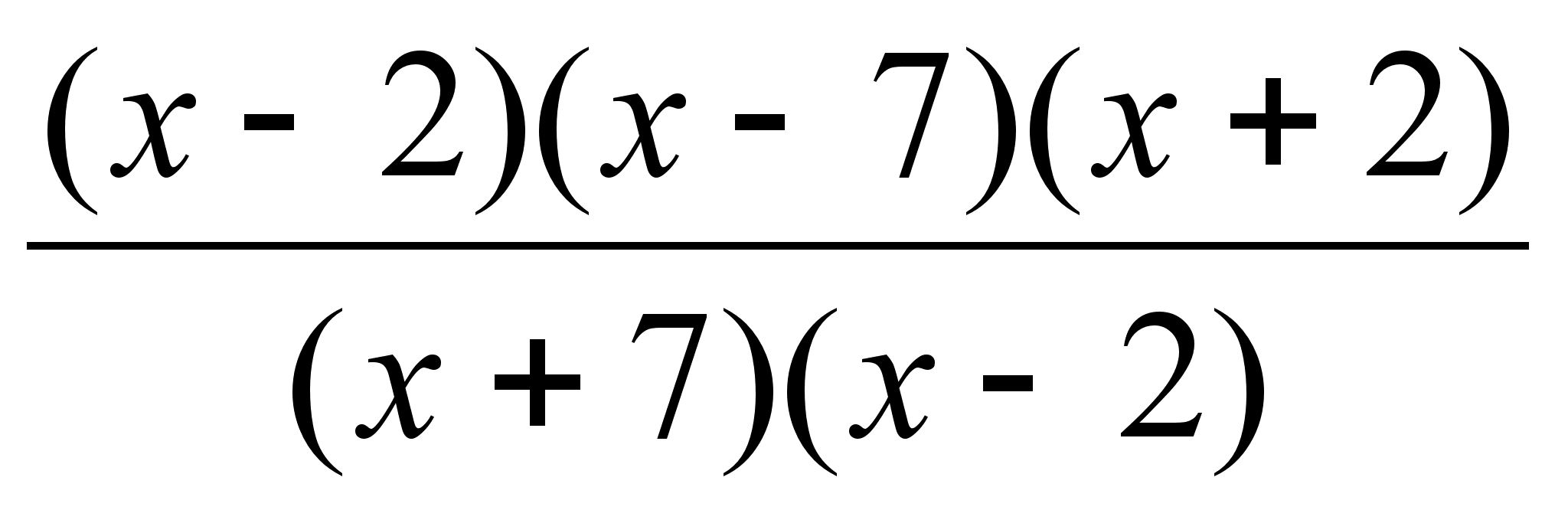 =
=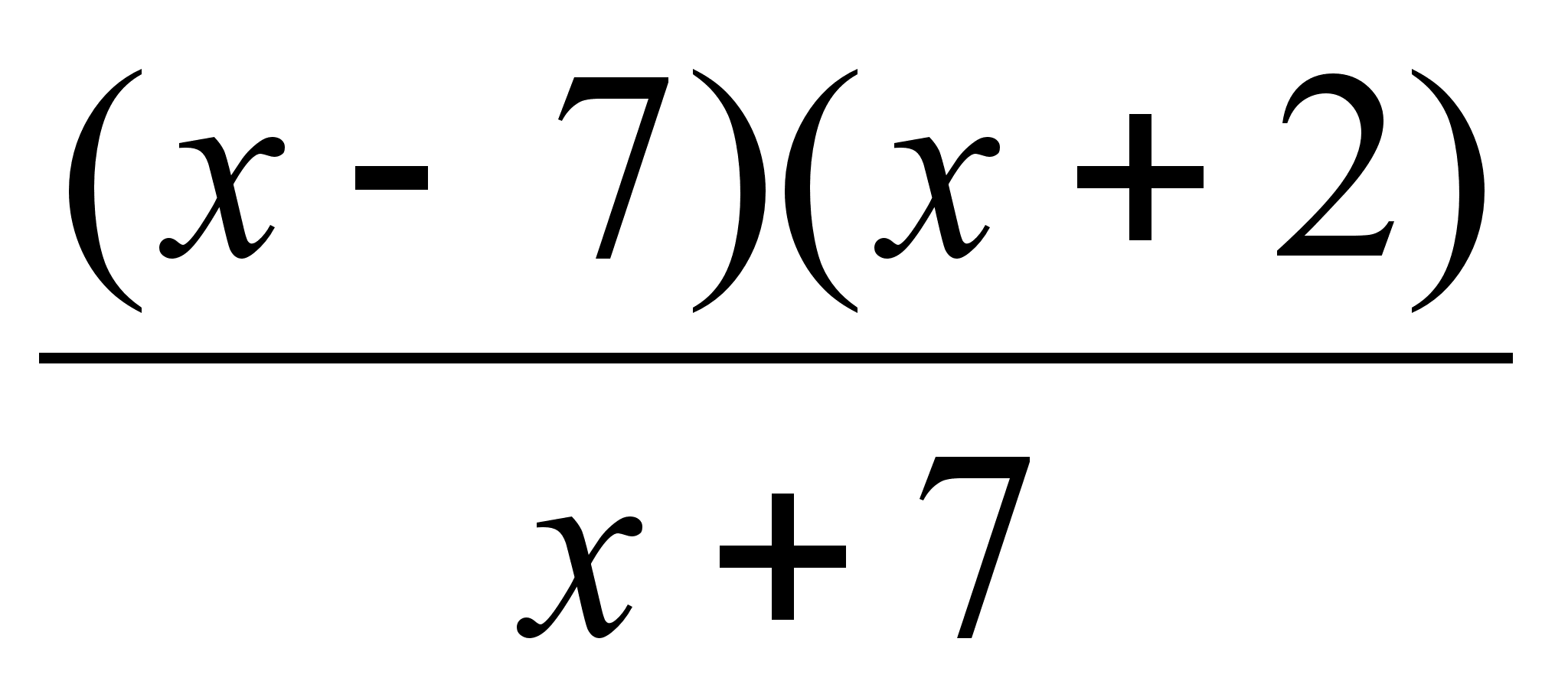 при
при
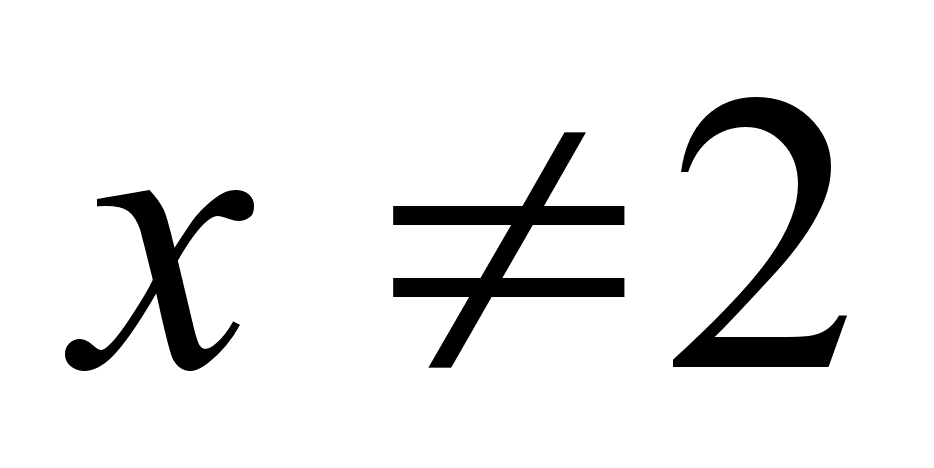 (корни
квадратного
трехчлена
найдены по
обратной теореме
Виета (в уме)),
(корни
квадратного
трехчлена
найдены по
обратной теореме
Виета (в уме)),
значит,
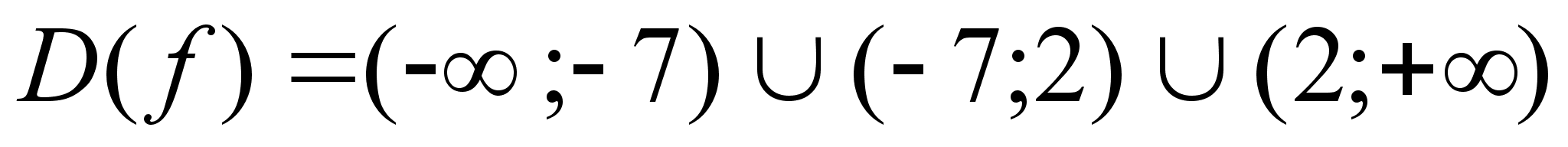 .
.
а) при
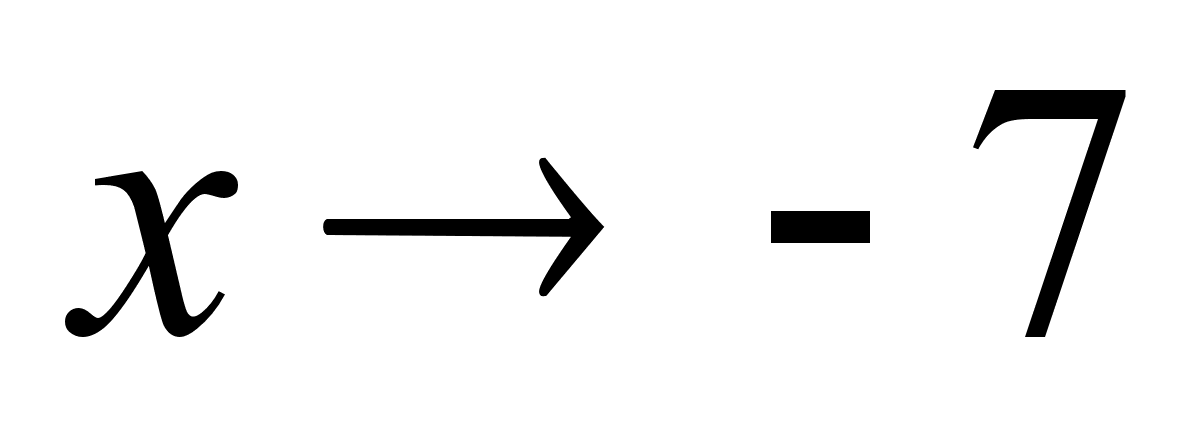 слева
слева
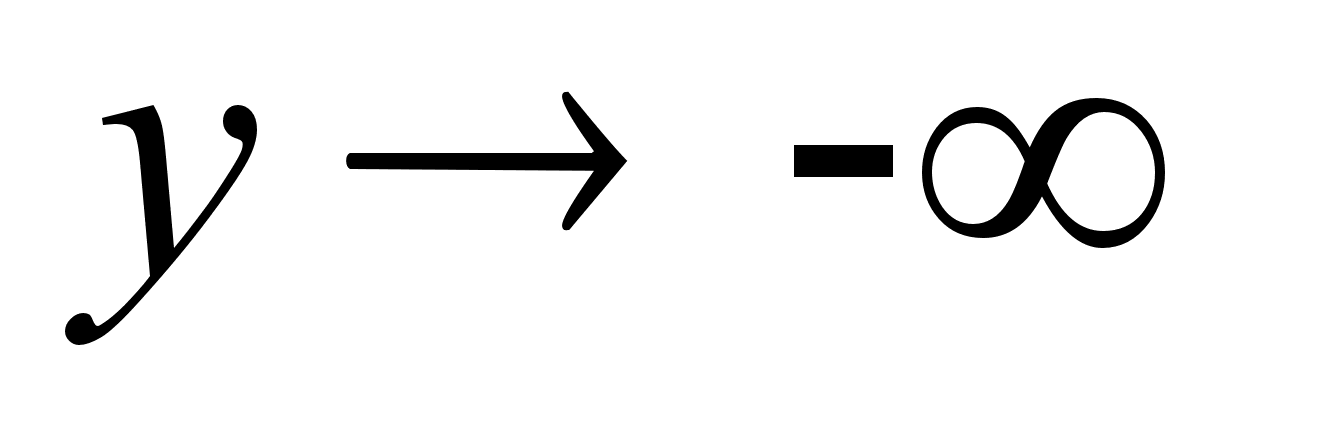 ;
(1)
;
(1)
-
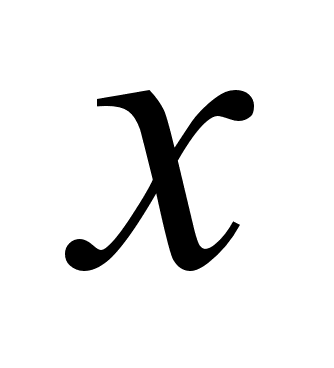
-8 -7,5 -7,1 … 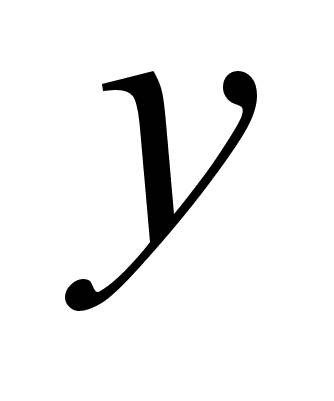
-90 -159,5 -719,1 …
при
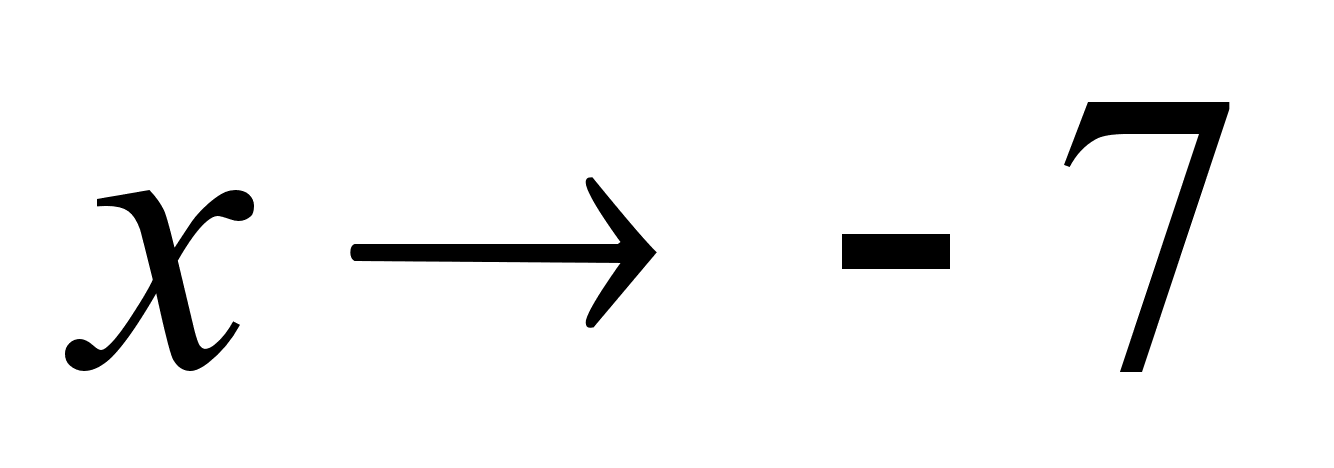 справа
справа
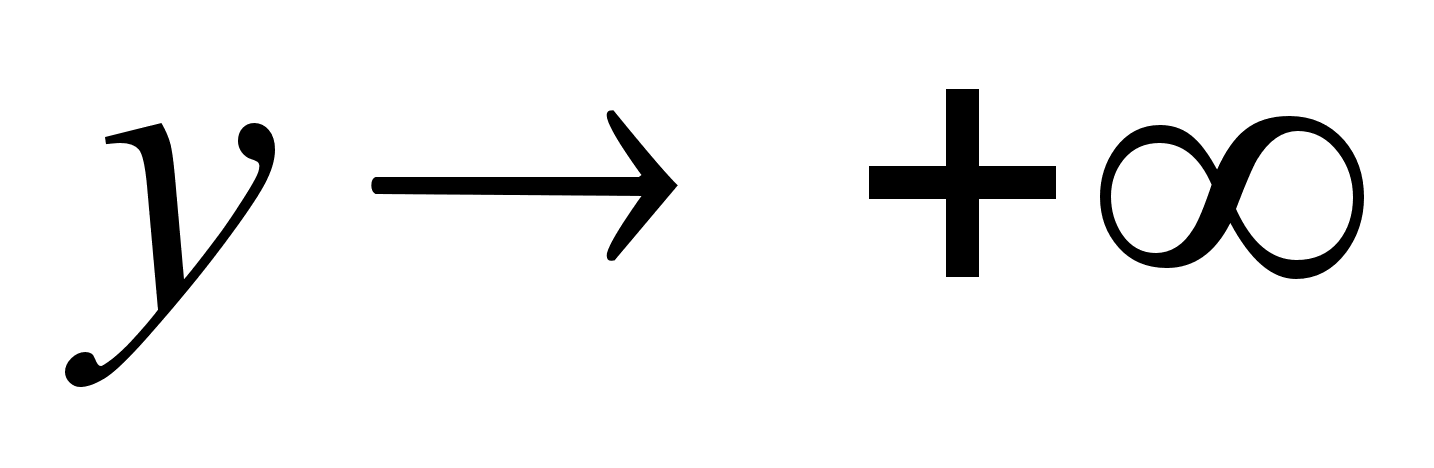 ;
(2)
;
(2)
-
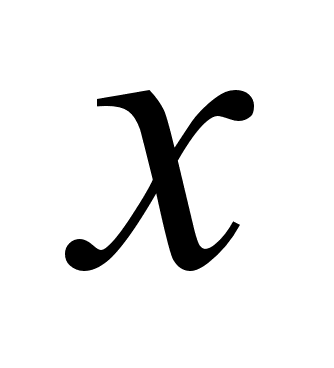
-6 -6,5 -6,9 … 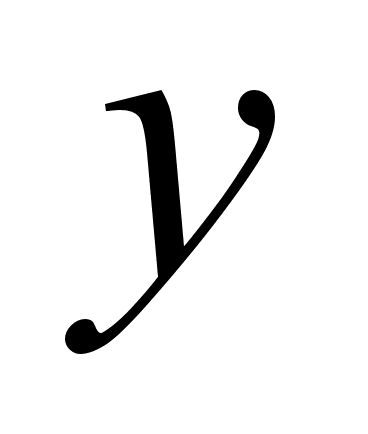
52 121,5 681,1 …
Значит,
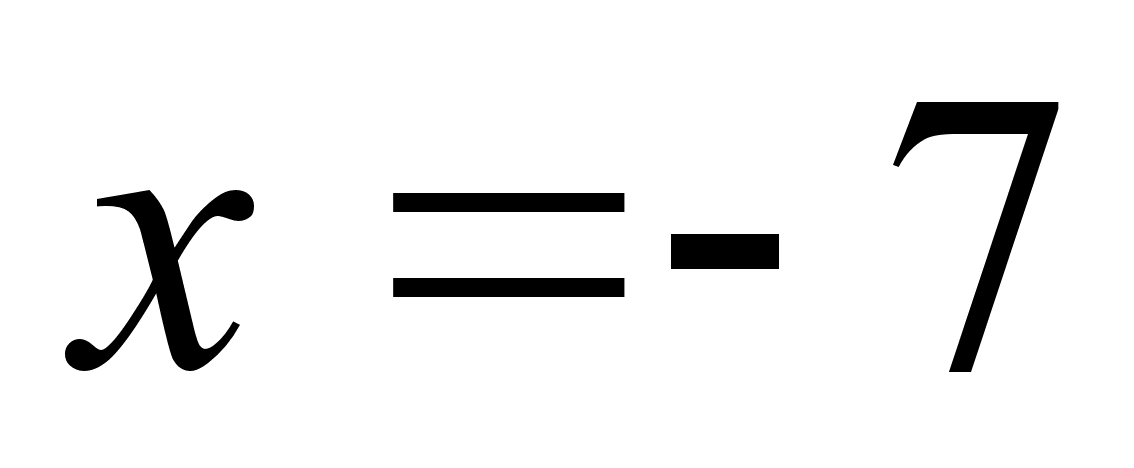 - вертикальная
асимптота;
- вертикальная
асимптота;
б) при
 (и слева и справа)
(и слева и справа)
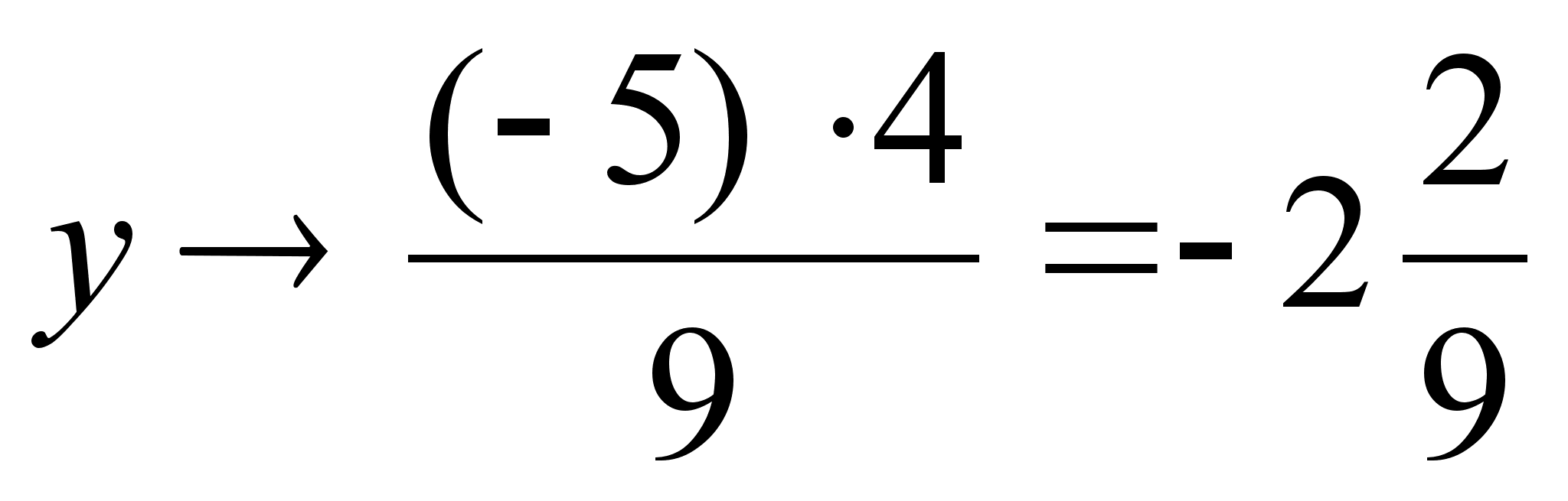 ;
;
-

1,9 2,1 
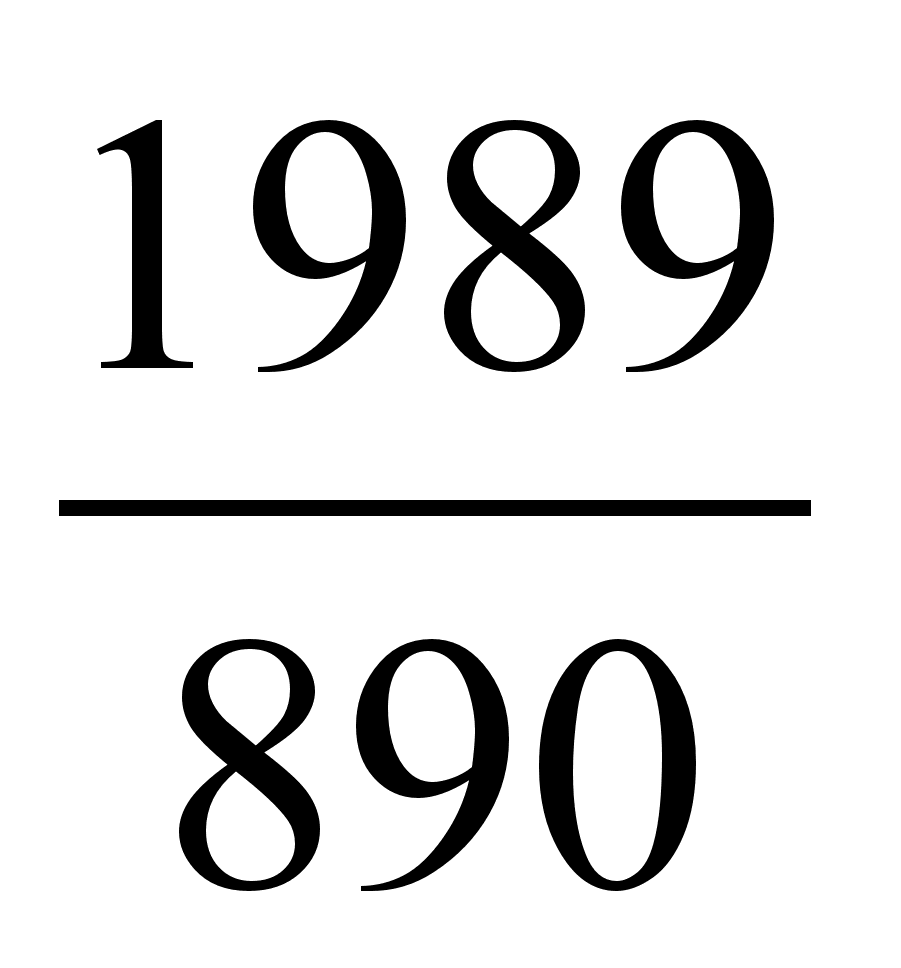
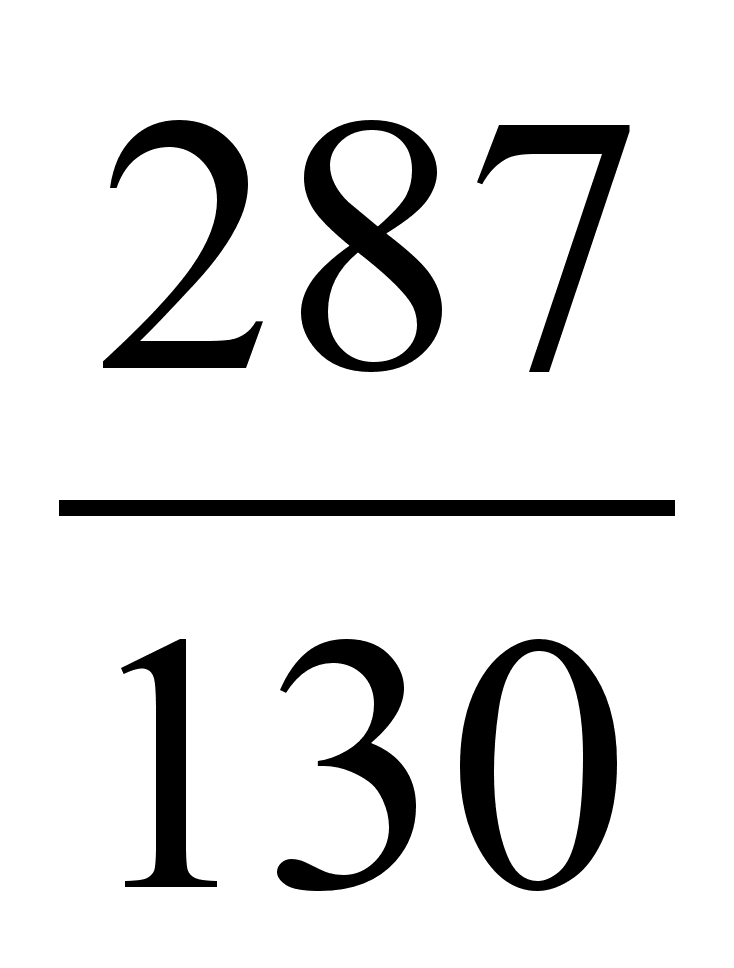
асимптоты
нет;
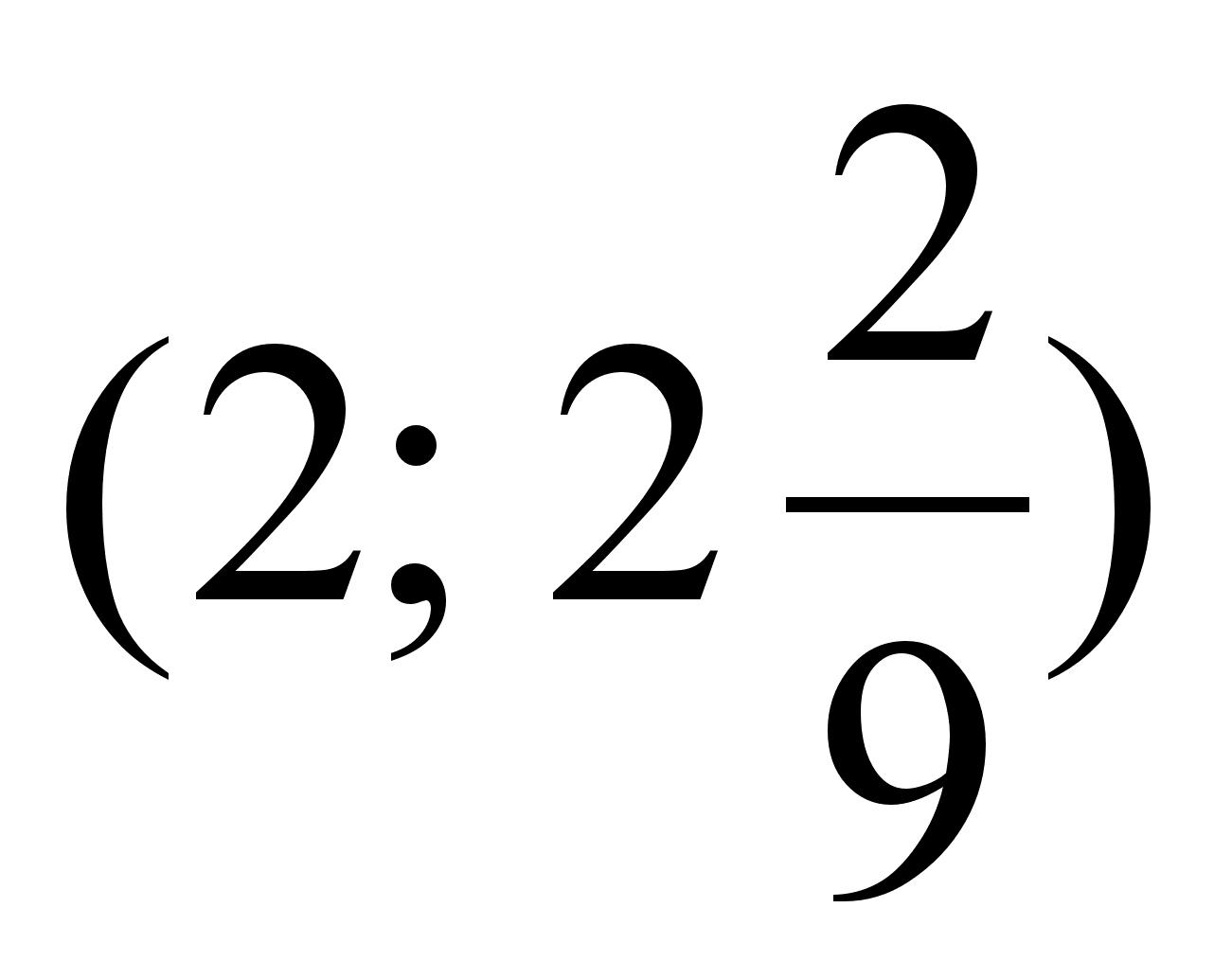 - исключенная
точка (т. разрыва).
(3)
- исключенная
точка (т. разрыва).
(3)
В
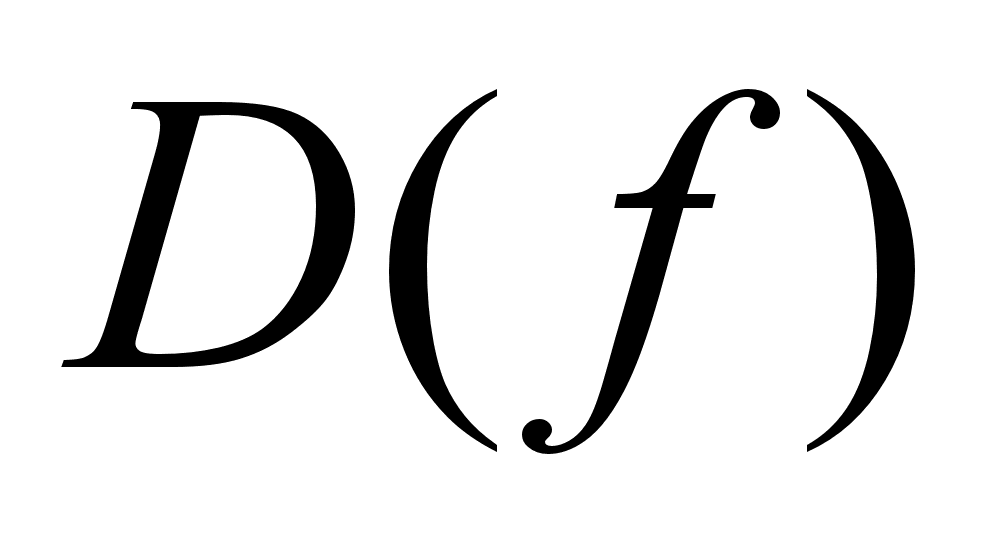
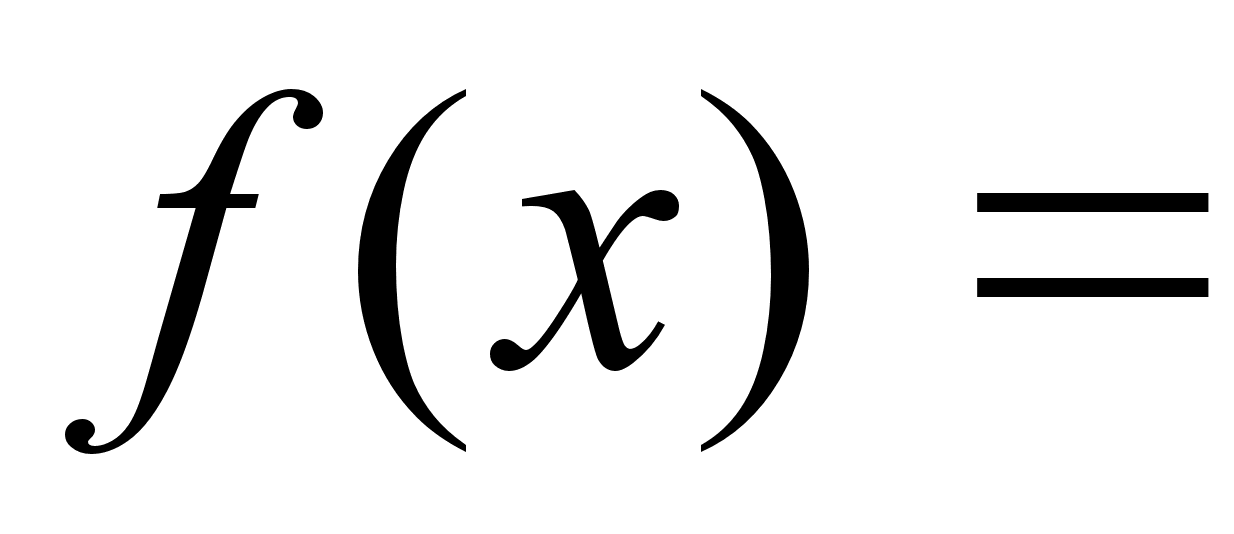
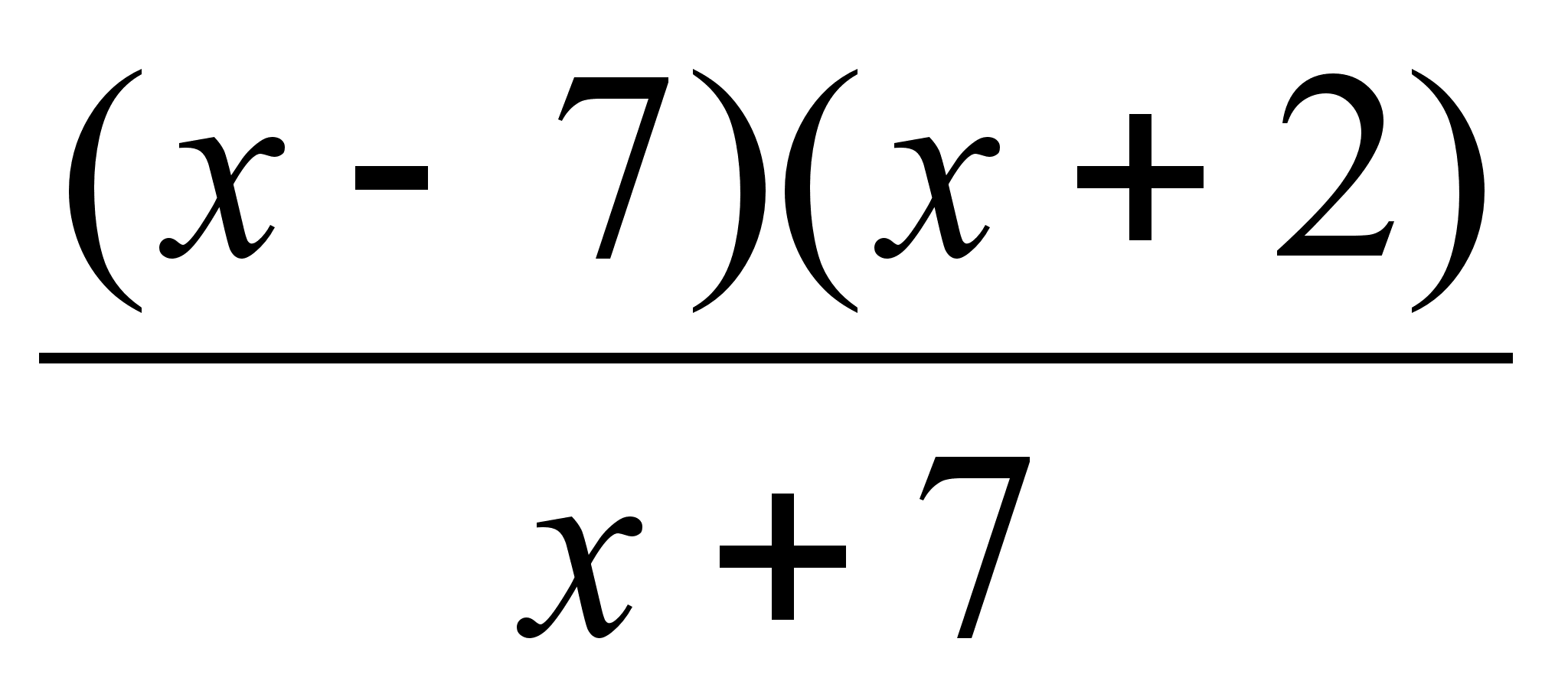
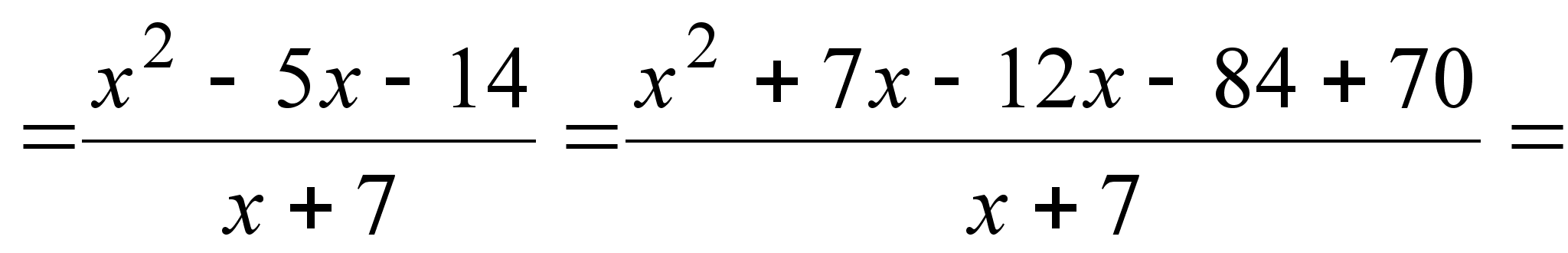
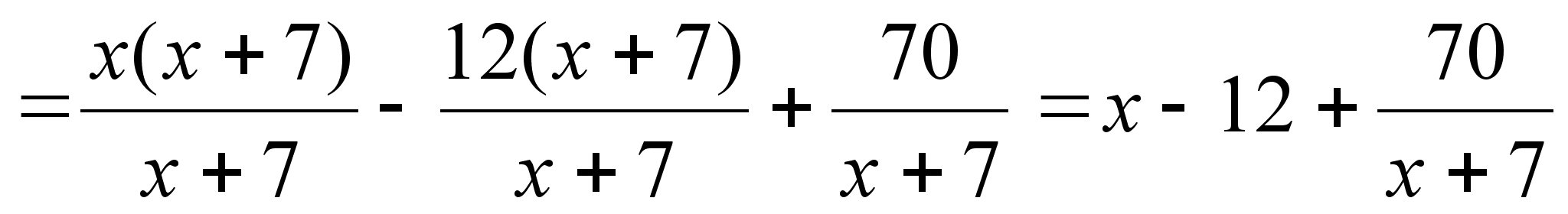 ;
т.к. при
;
т.к. при
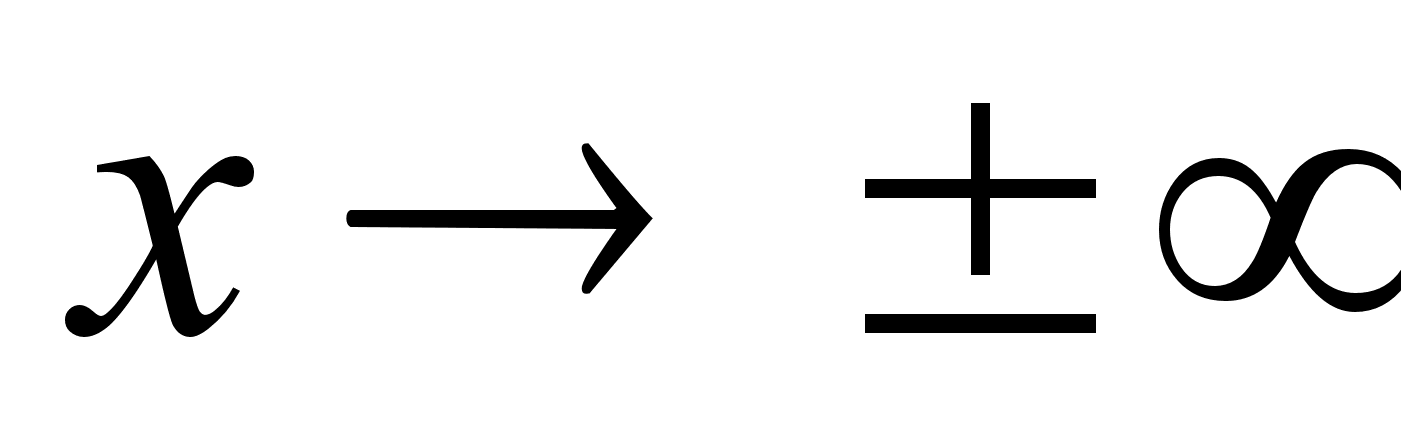
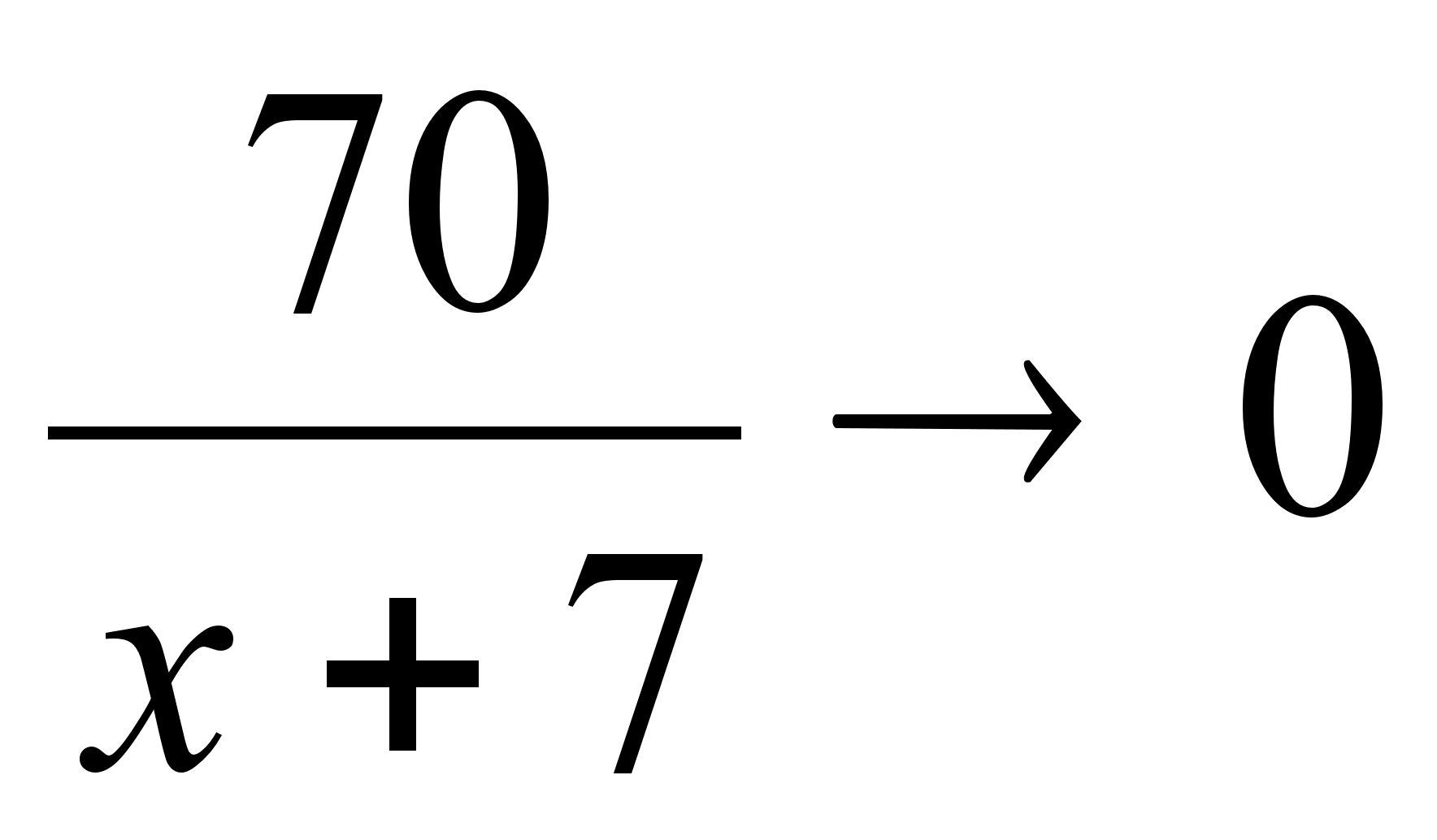 ,
то
,
то
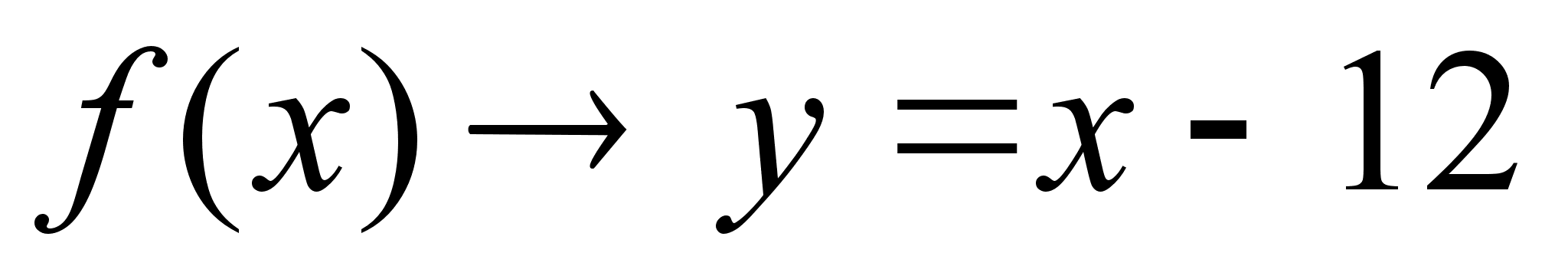 ;
таким образом,
прямая
;
таким образом,
прямая
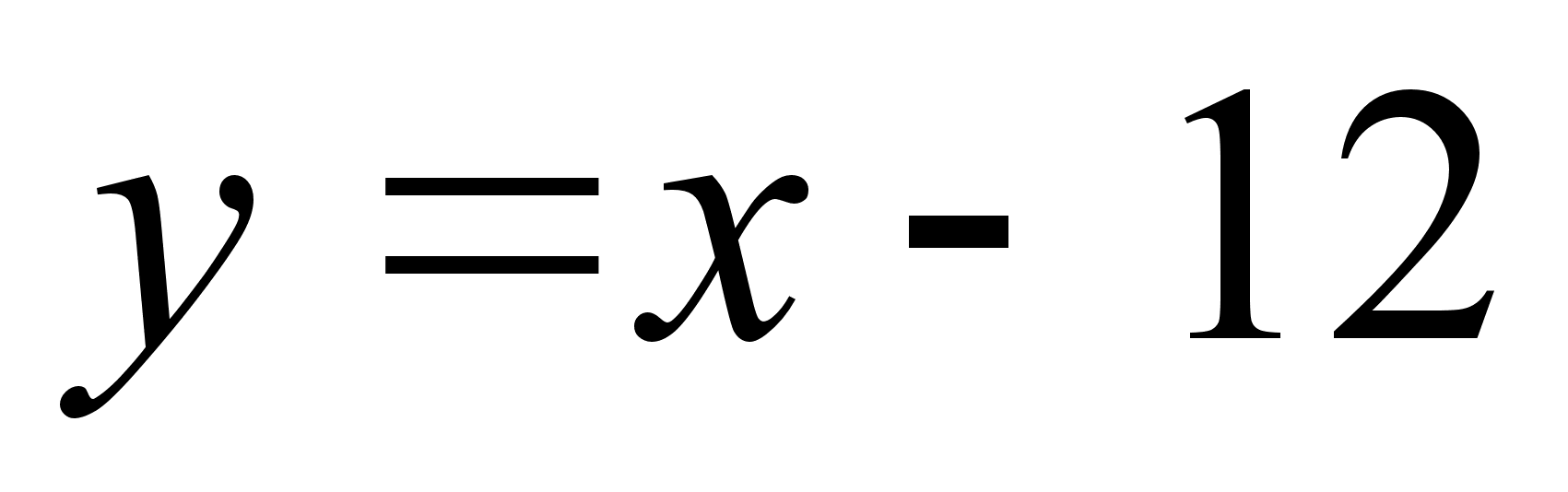 - наклонная
асимптота.
- наклонная
асимптота.
Исследуем на четность:
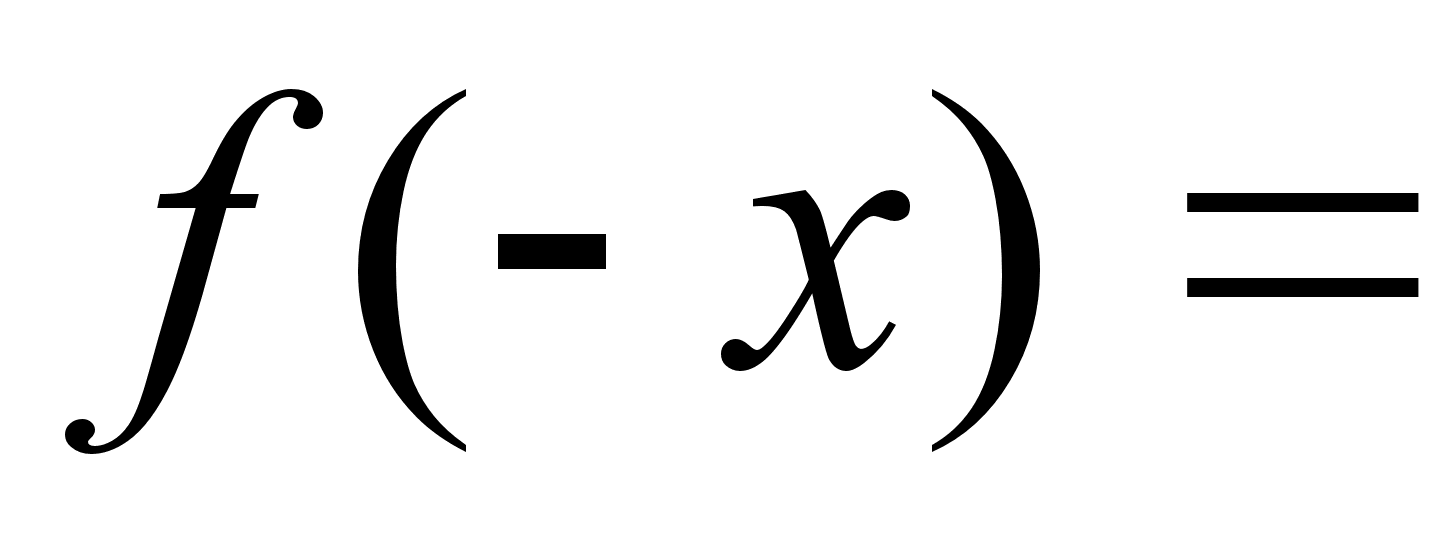
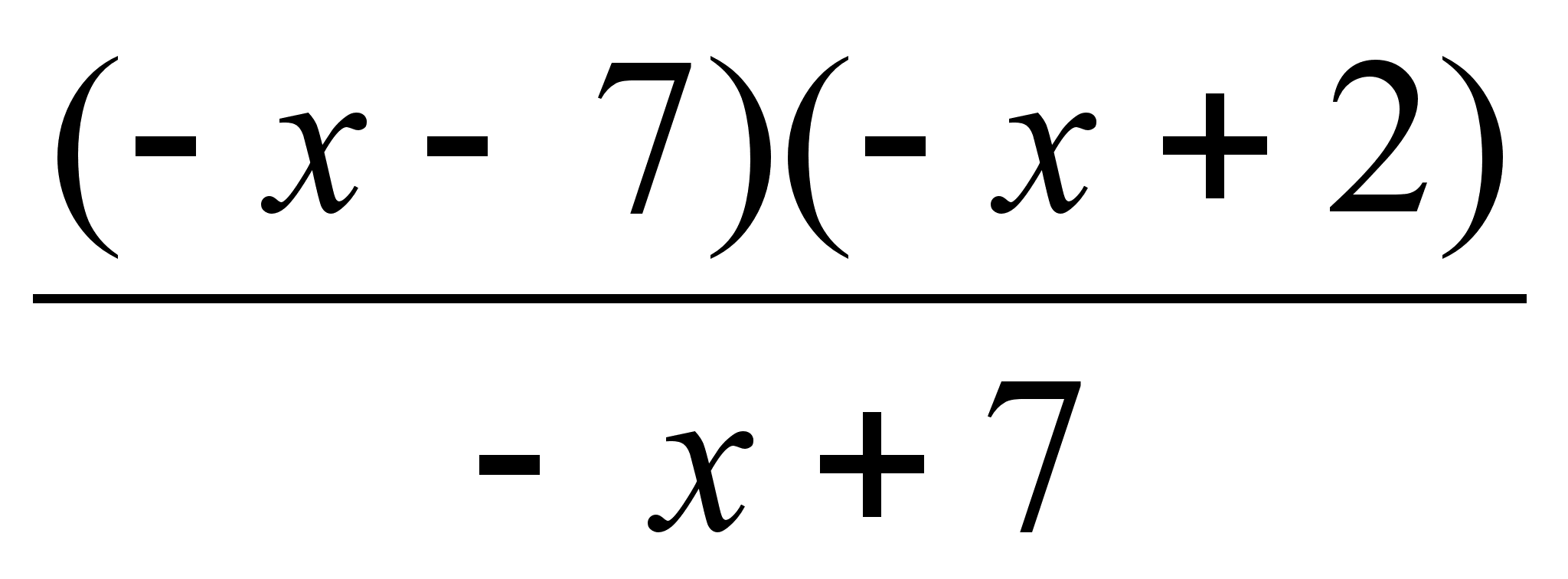
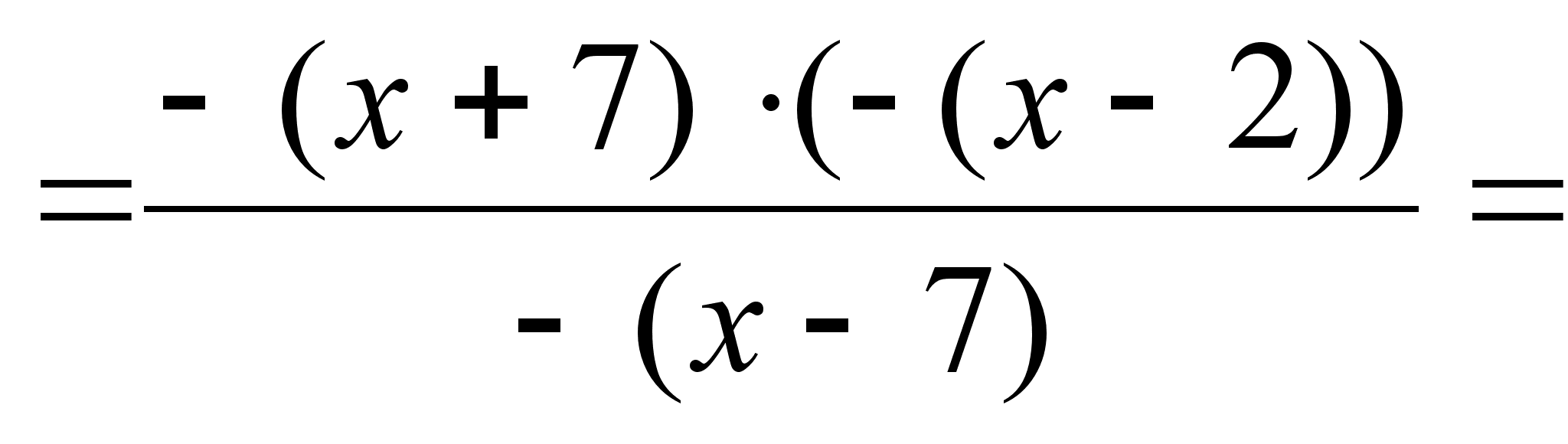
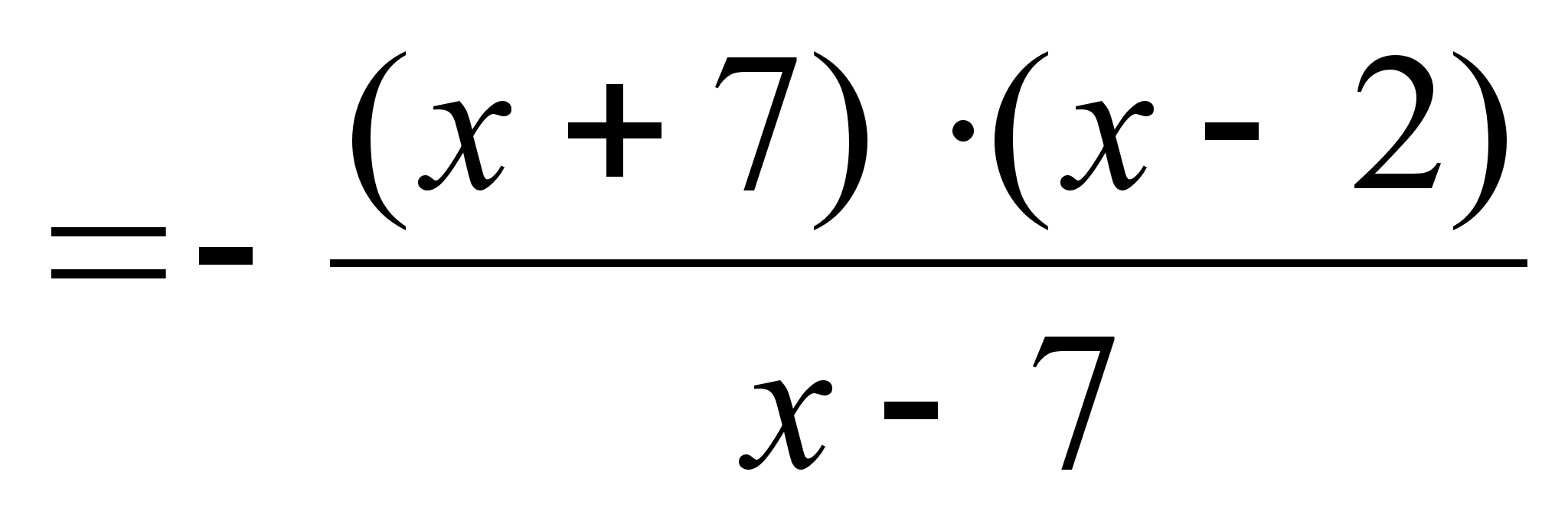 ;
видим, что:
;
видим, что:
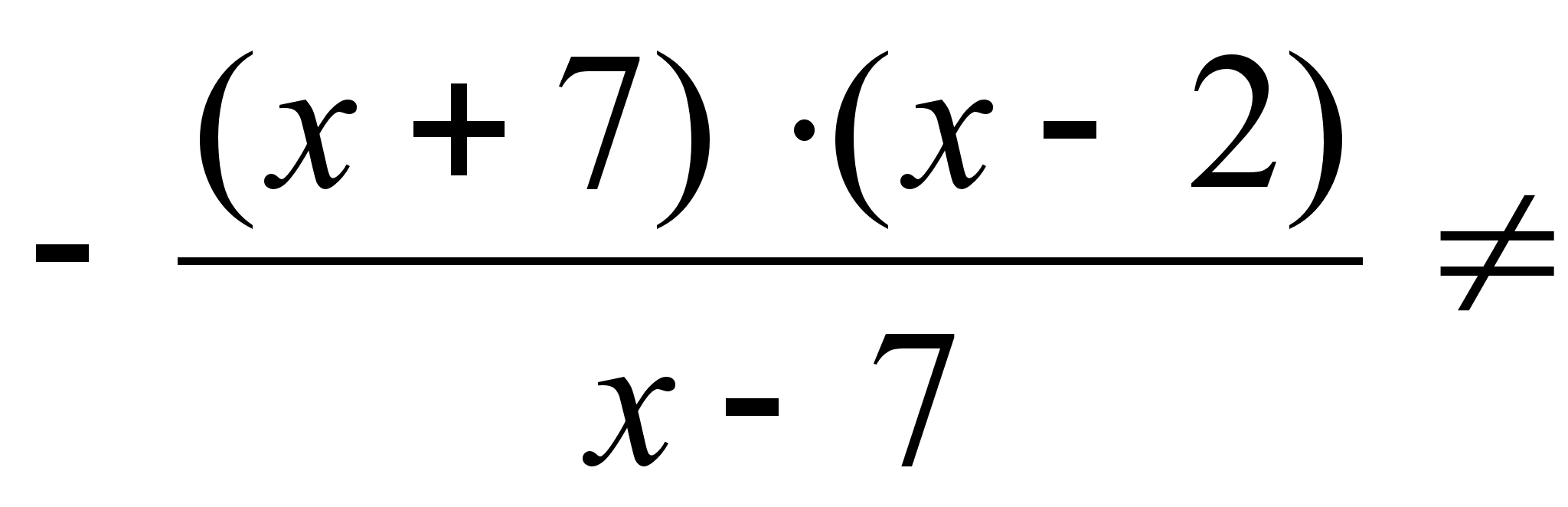
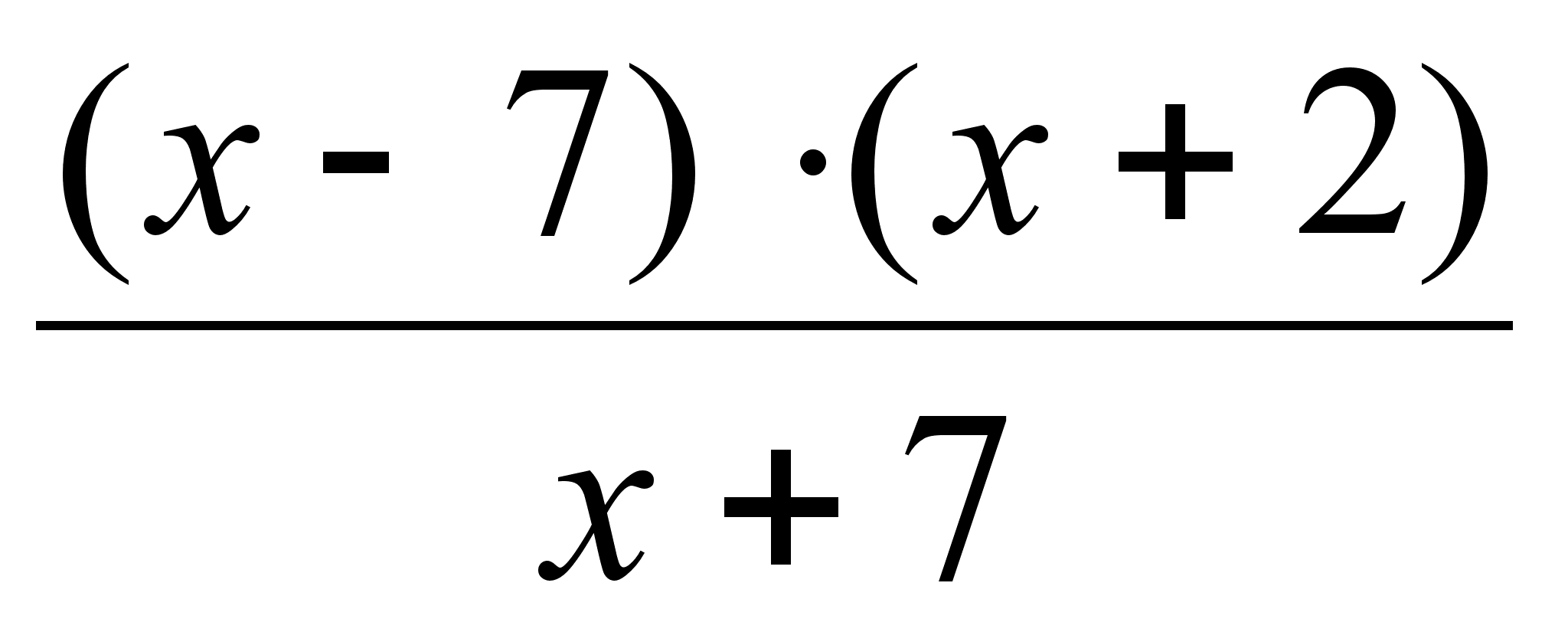 и
и
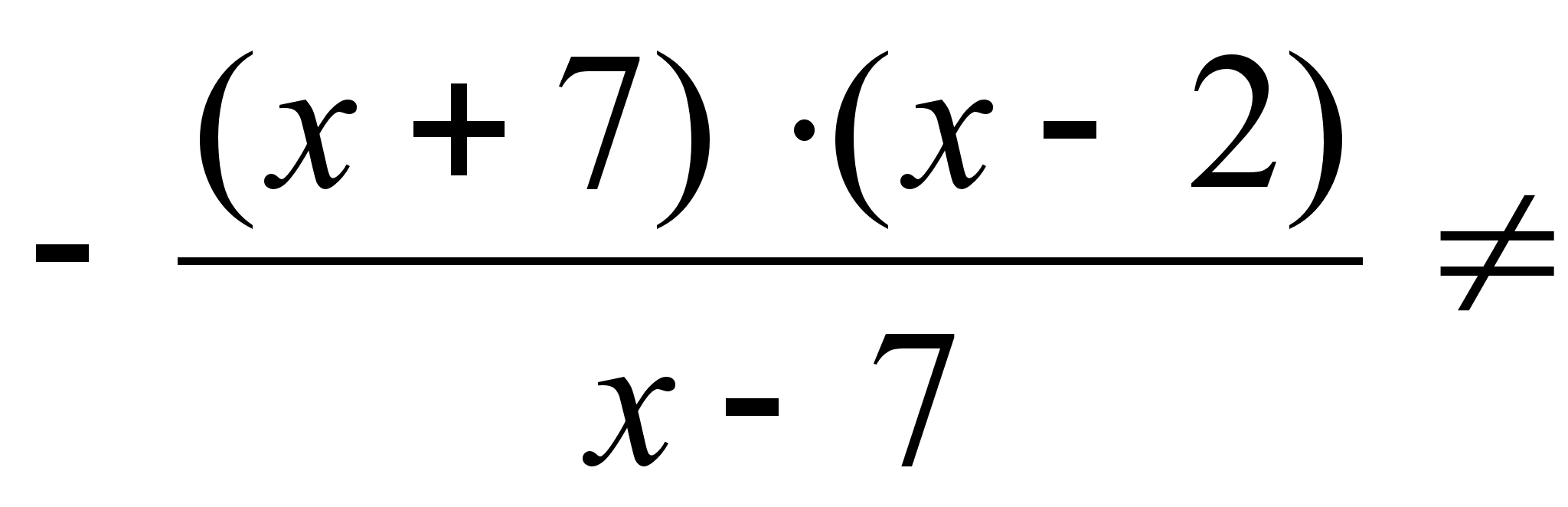
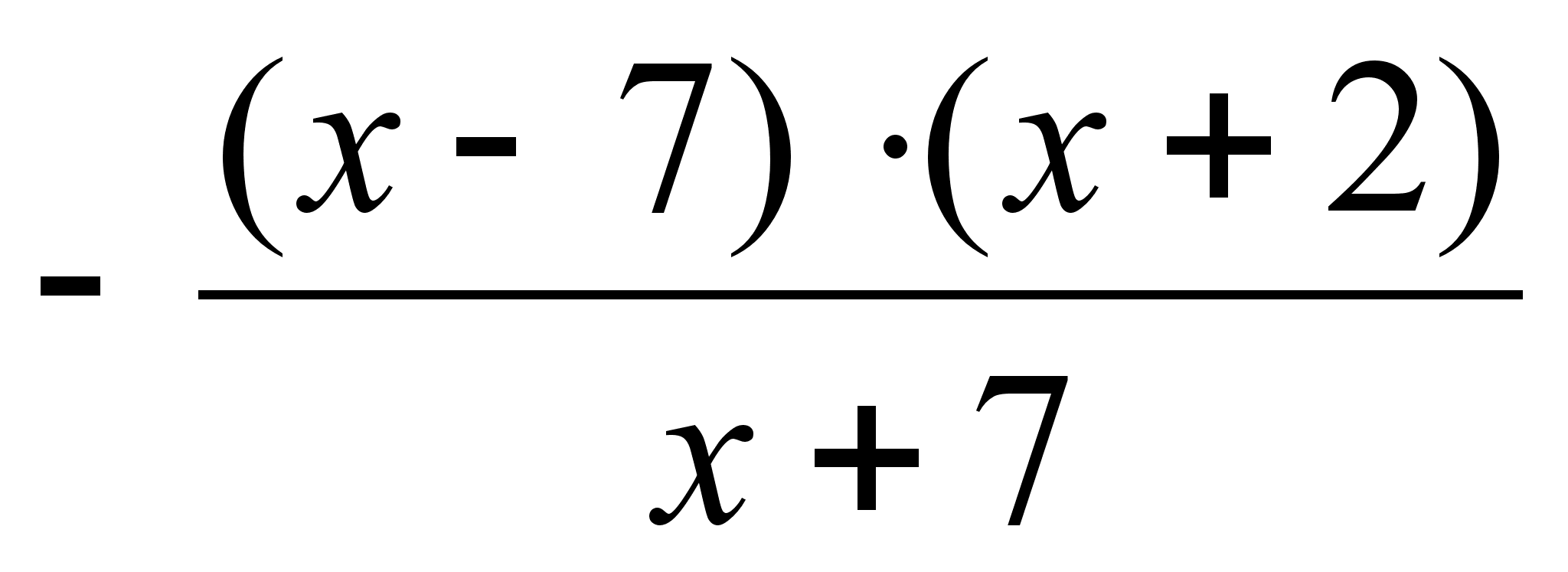 ,
т.е.
,
т.е.
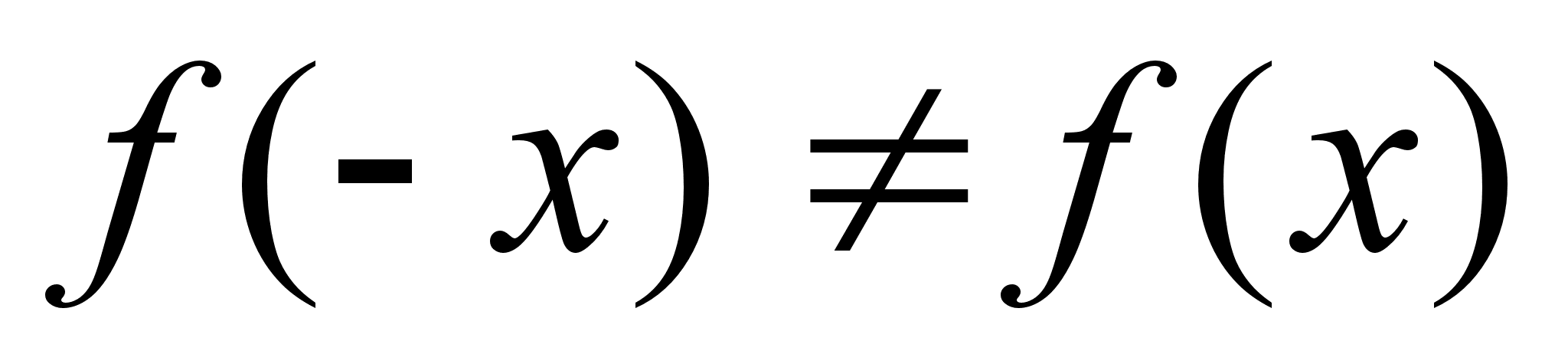 и
и
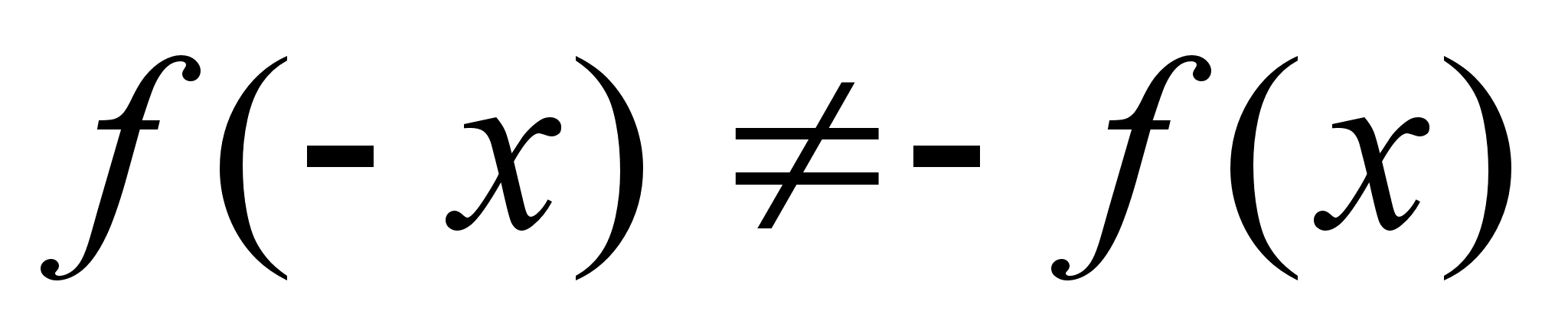 ,
значит,
,
значит,
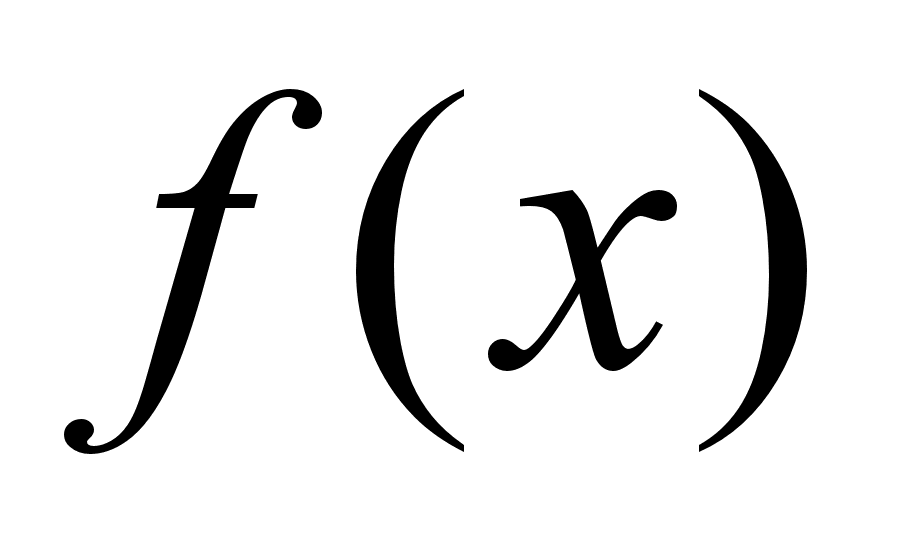 общего вида
(не обладает
ни четностью,
ни нечетностью);
общего вида
(не обладает
ни четностью,
ни нечетностью);
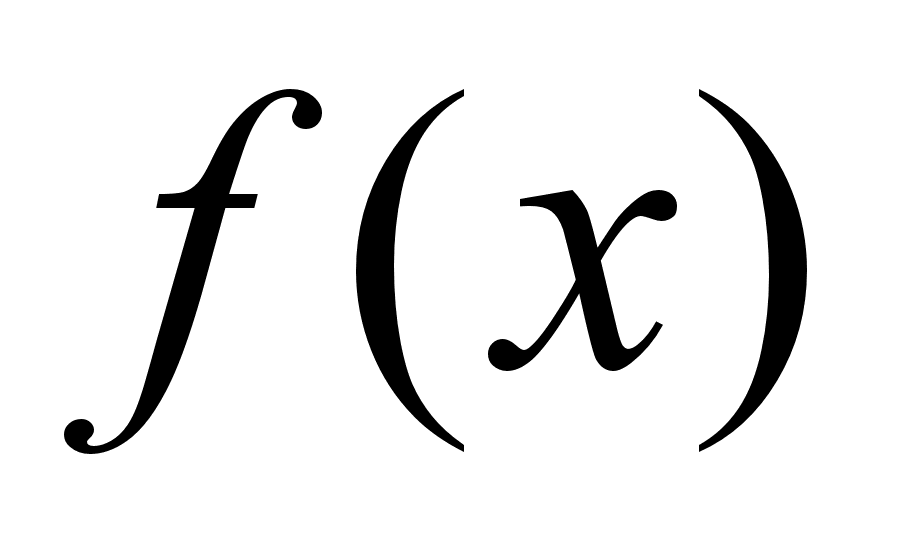 не является
периодической
как дробно-рациональная
функция (многочлены
– непериодические
функции).
не является
периодической
как дробно-рациональная
функция (многочлены
– непериодические
функции).
а) при
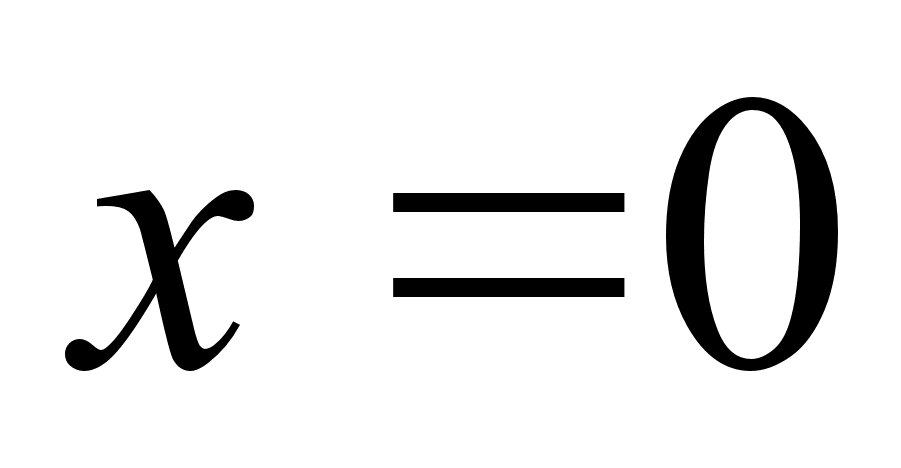
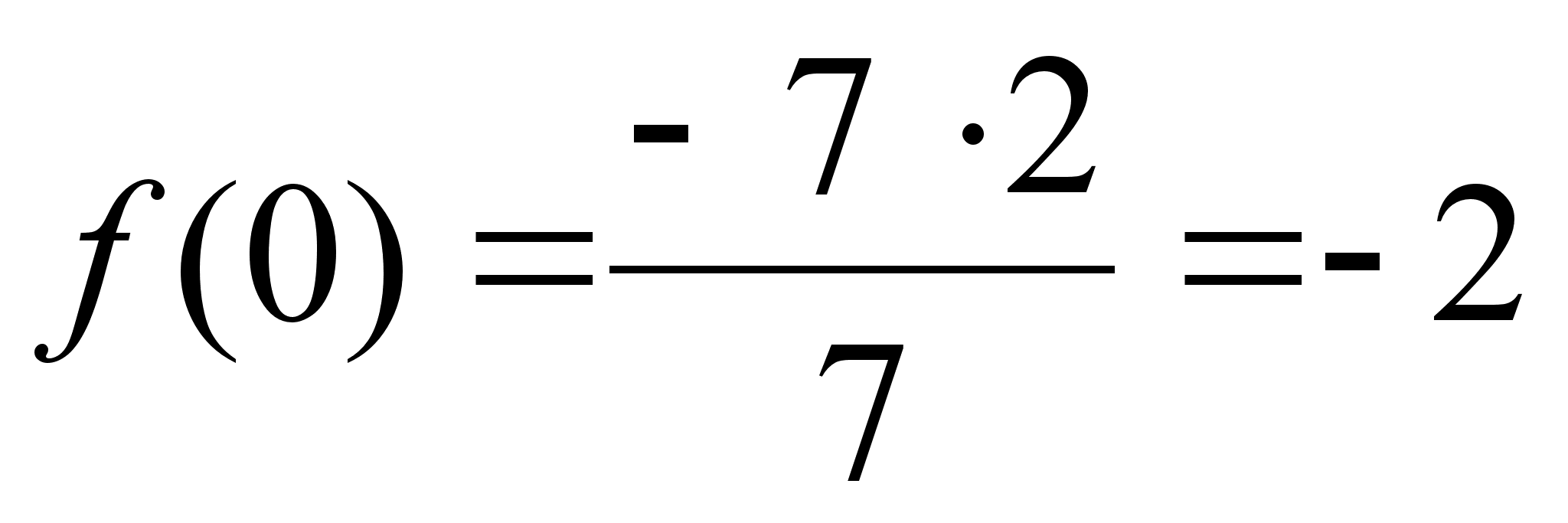 ;
значит,
;
значит,
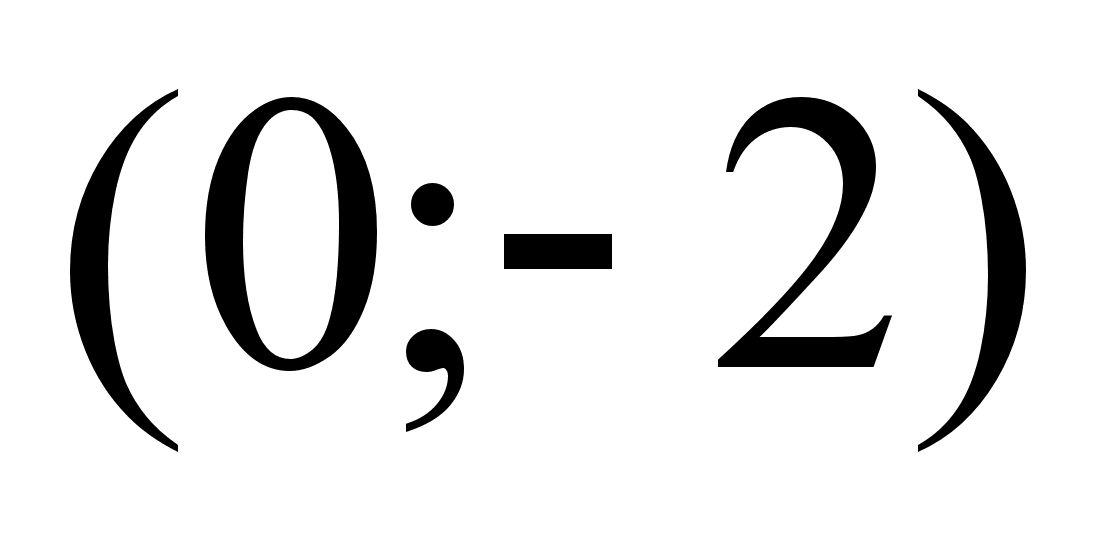 - точка пересечения
графика с осью
ординат;
(4)
- точка пересечения
графика с осью
ординат;
(4)
б)
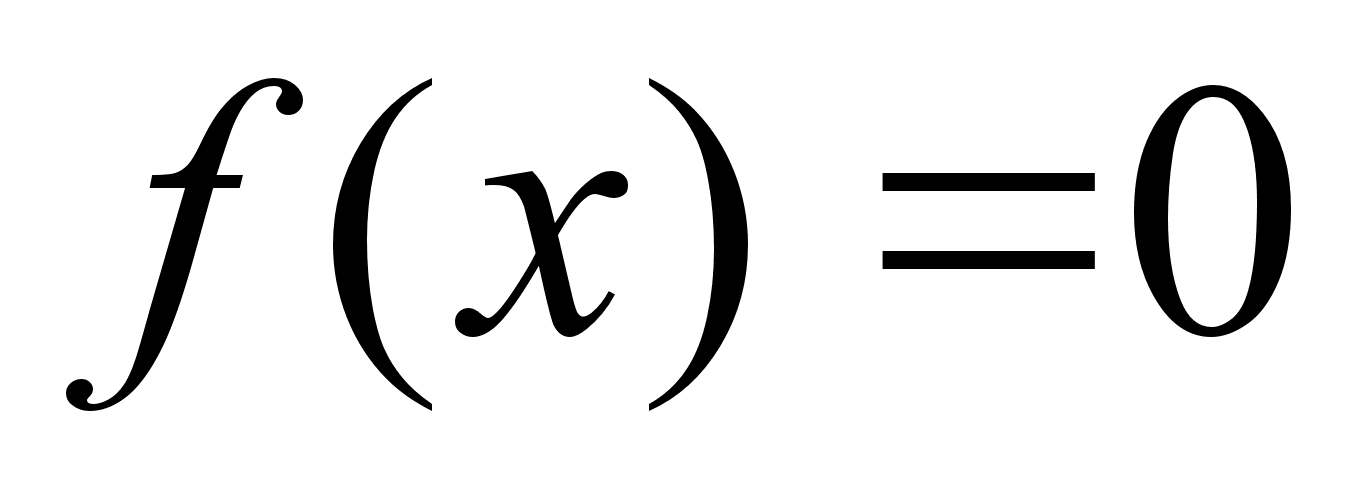 при
при
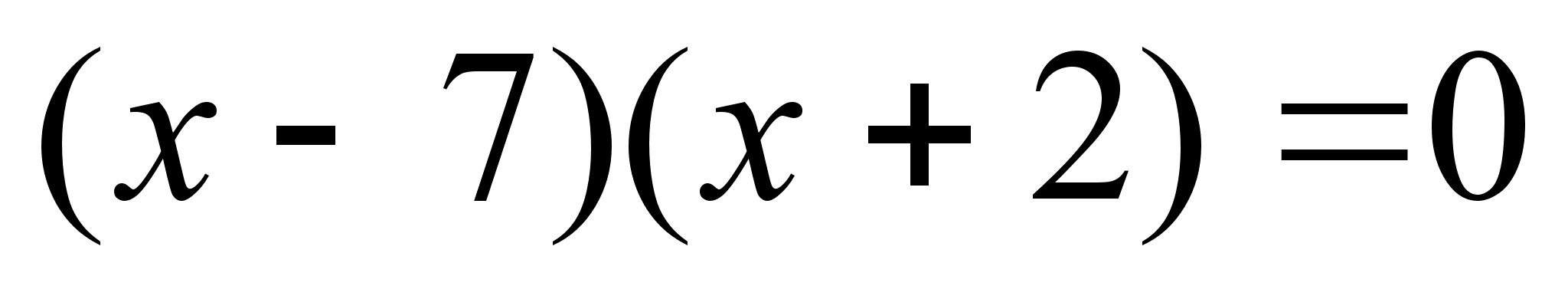 ,
но
,
но
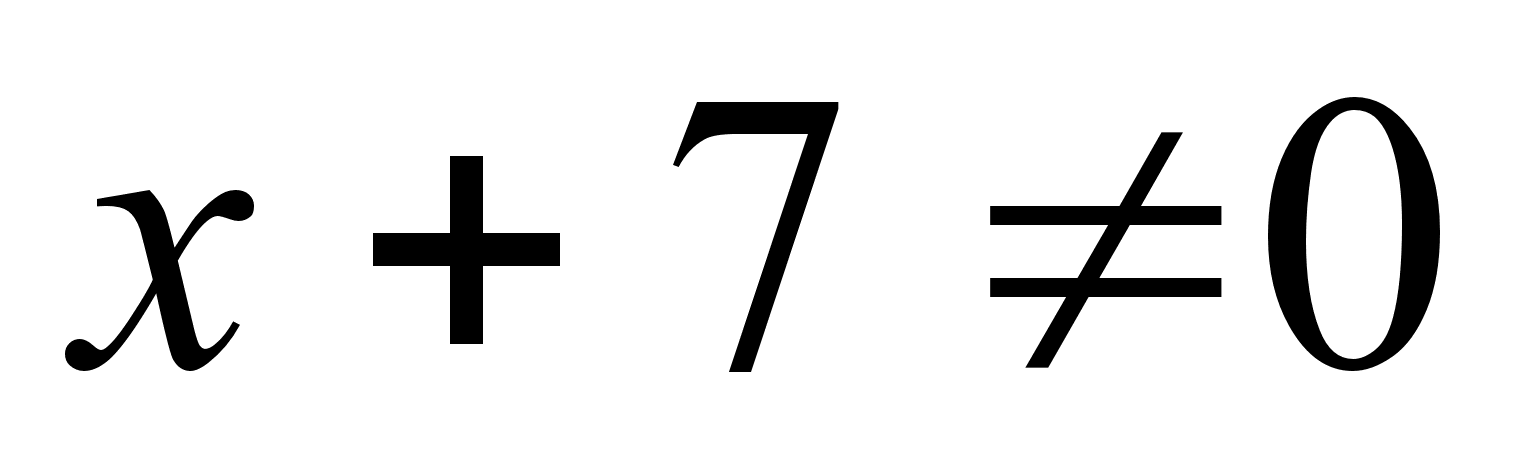 ,
т.е. при
,
т.е. при
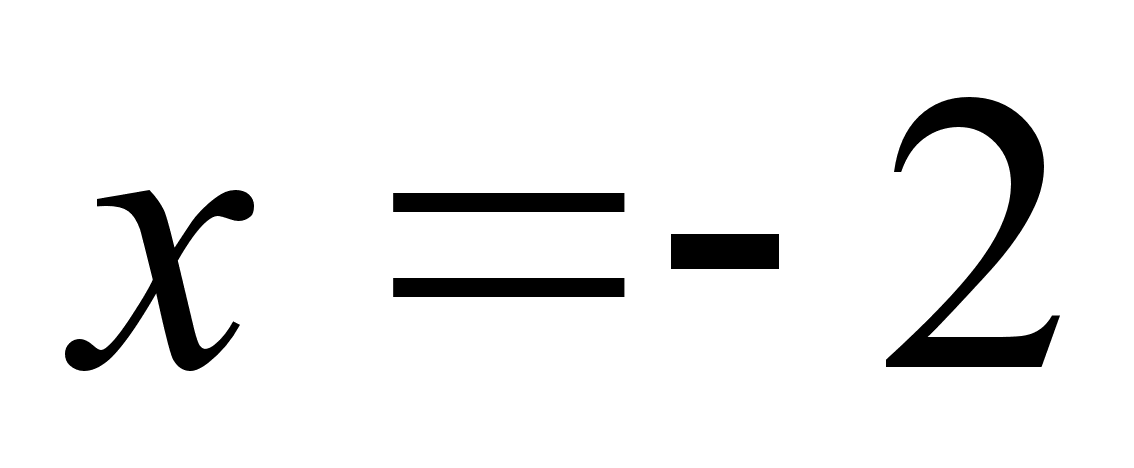 или
или
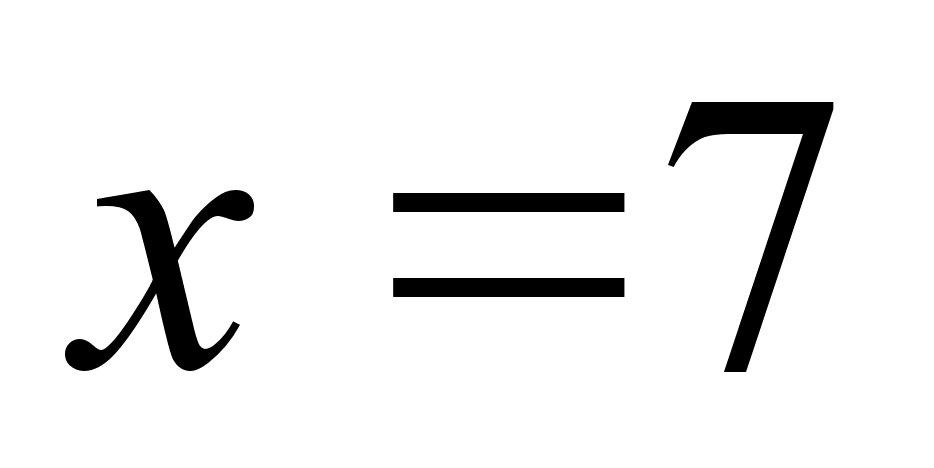 ,
т.о.
,
т.о.
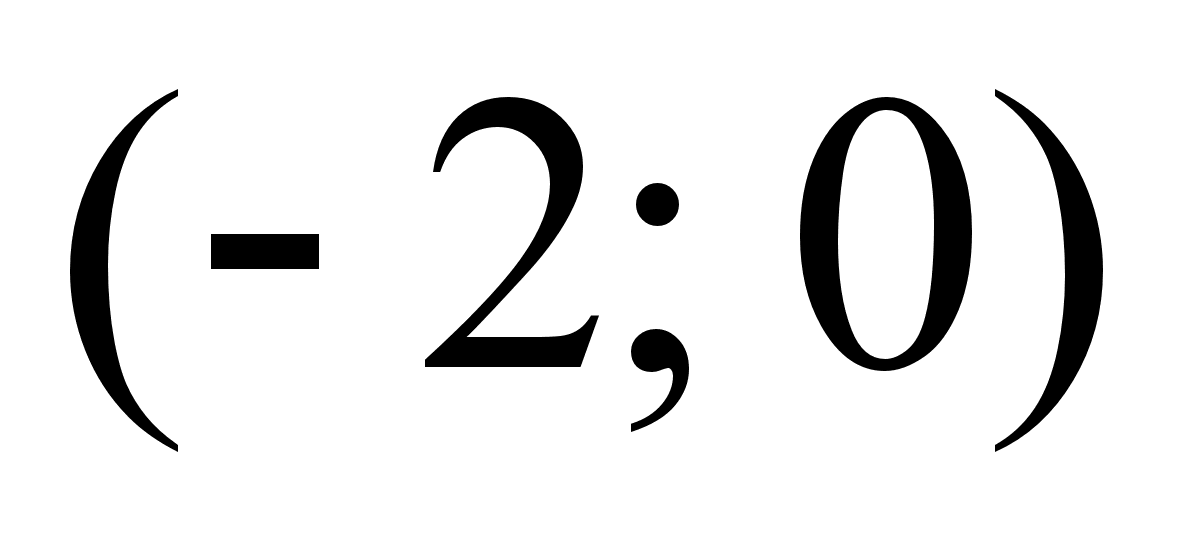 и
и
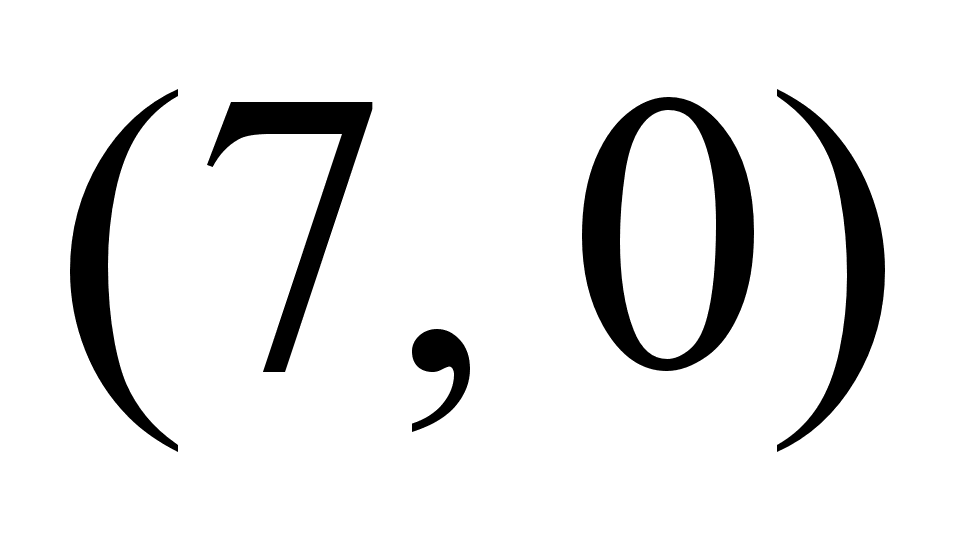 - точки пересечения
графика
- точки пересечения
графика
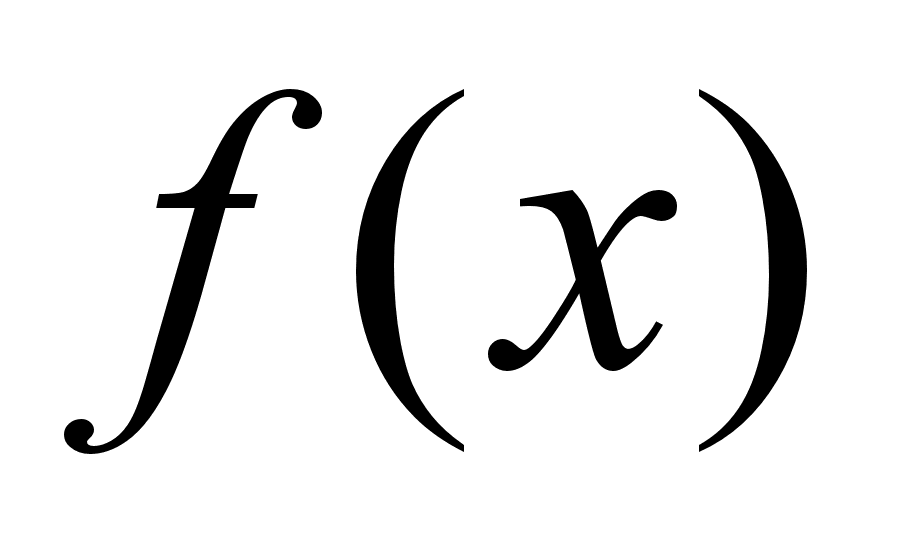 с осью абсцисс.
(5)
с осью абсцисс.
(5)
С учетом
точек разрыва
и найденных
значений функции
(по (1), (2), (3) и (4), (5)) получаем:
при
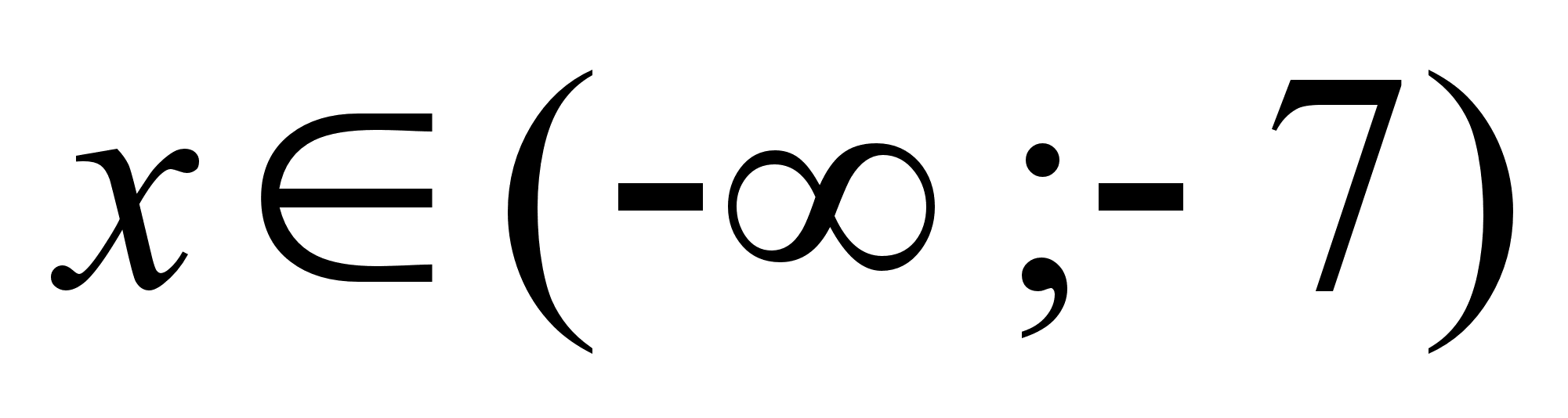
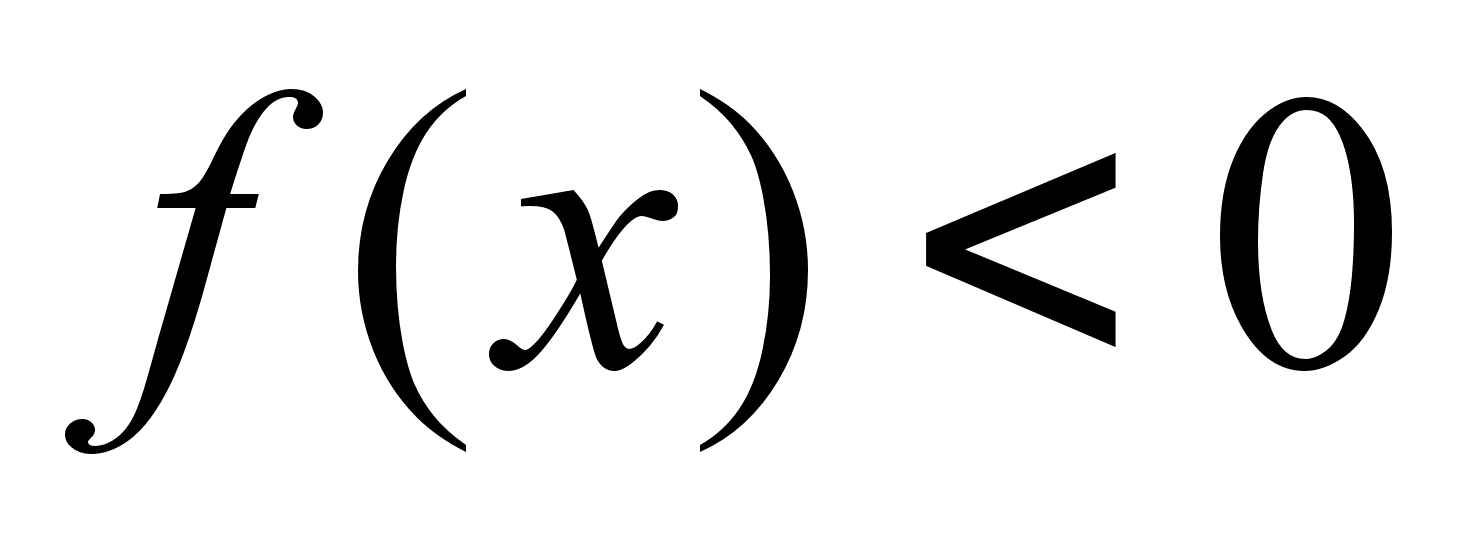 ;
при
;
при
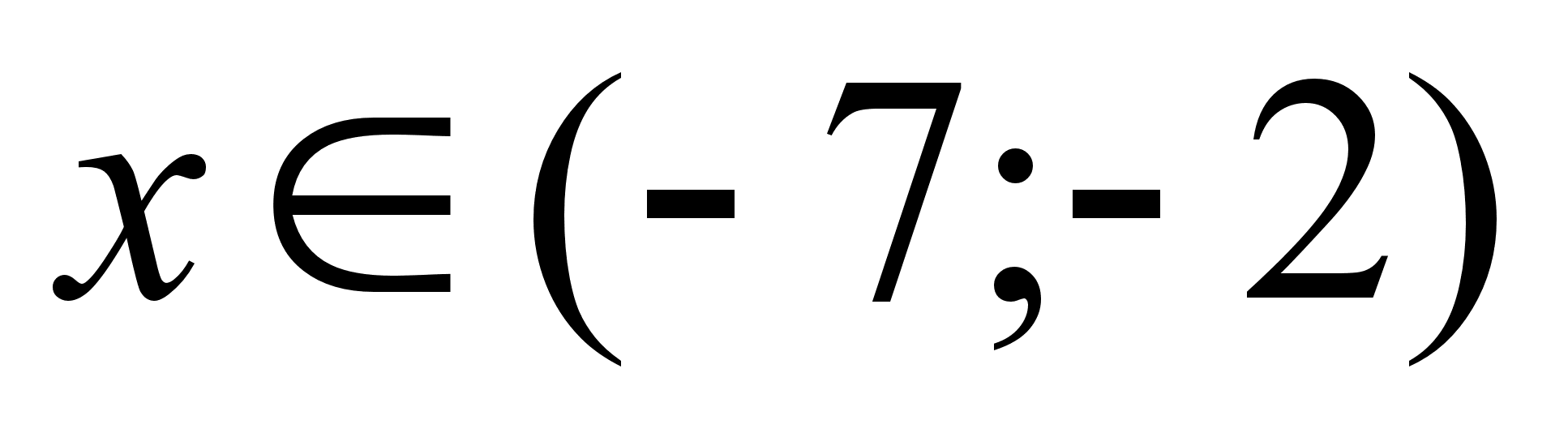
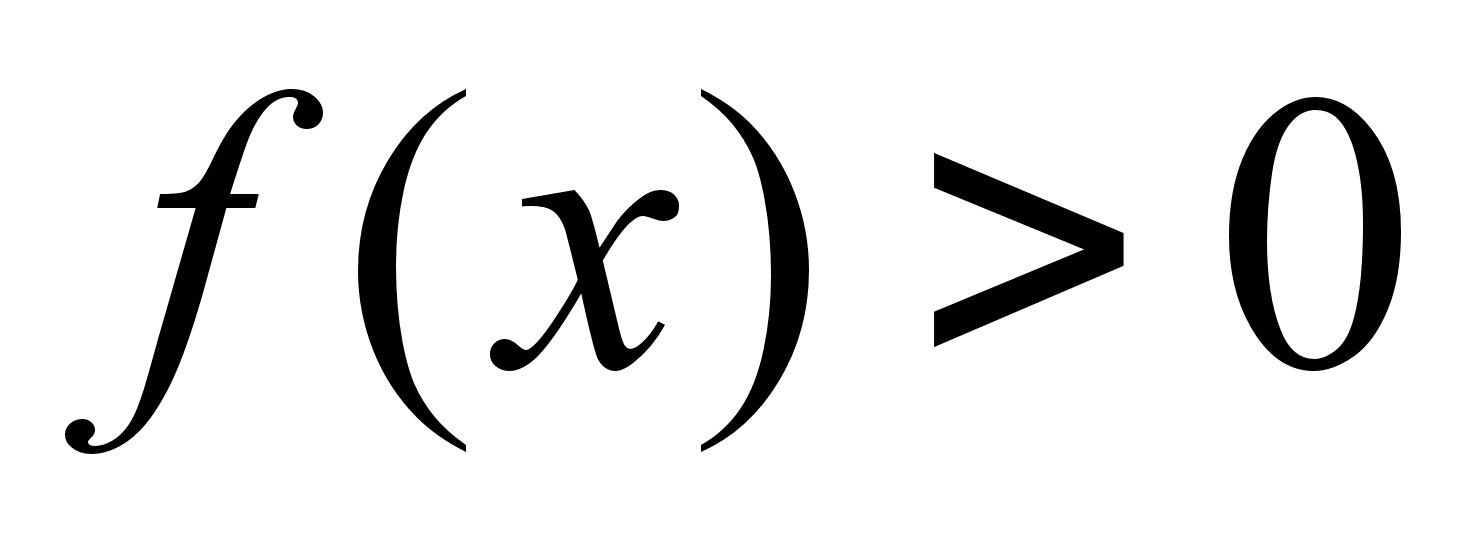 ;
;
при
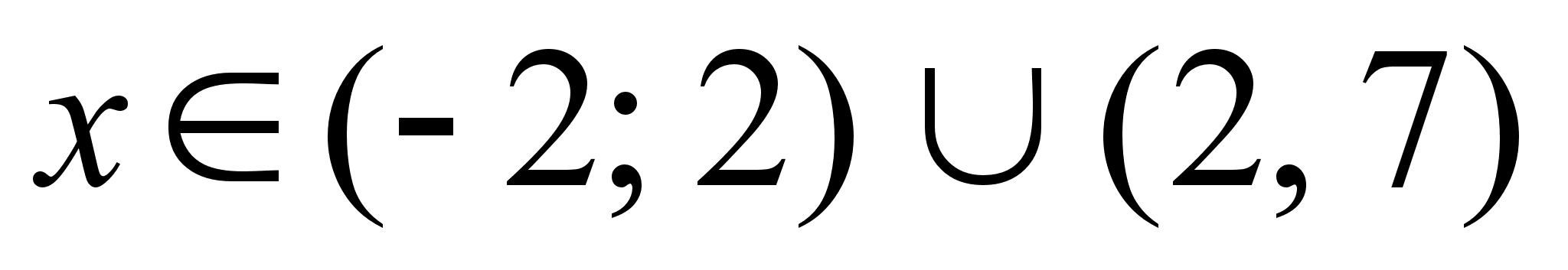
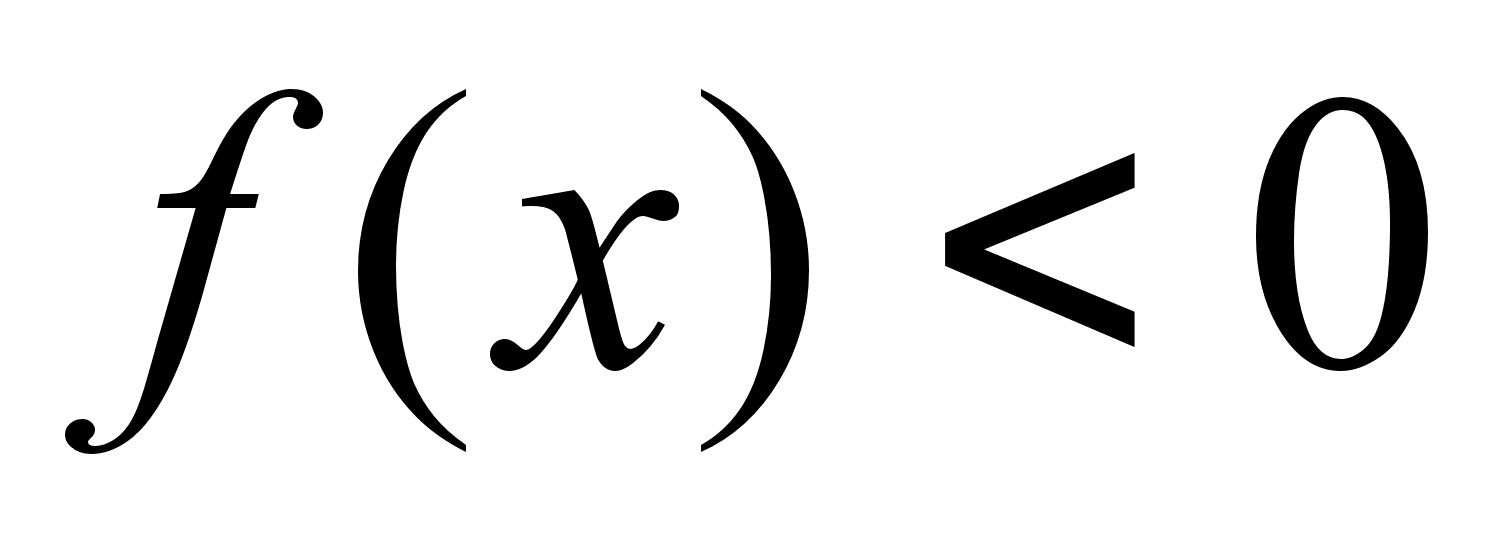 ;
при
;
при
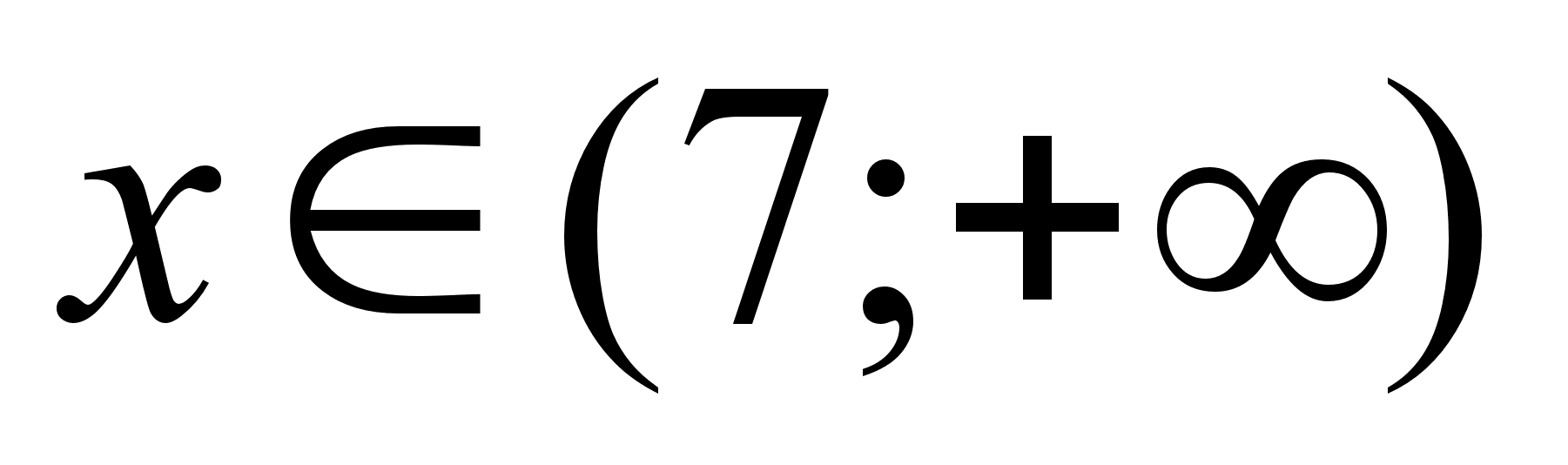
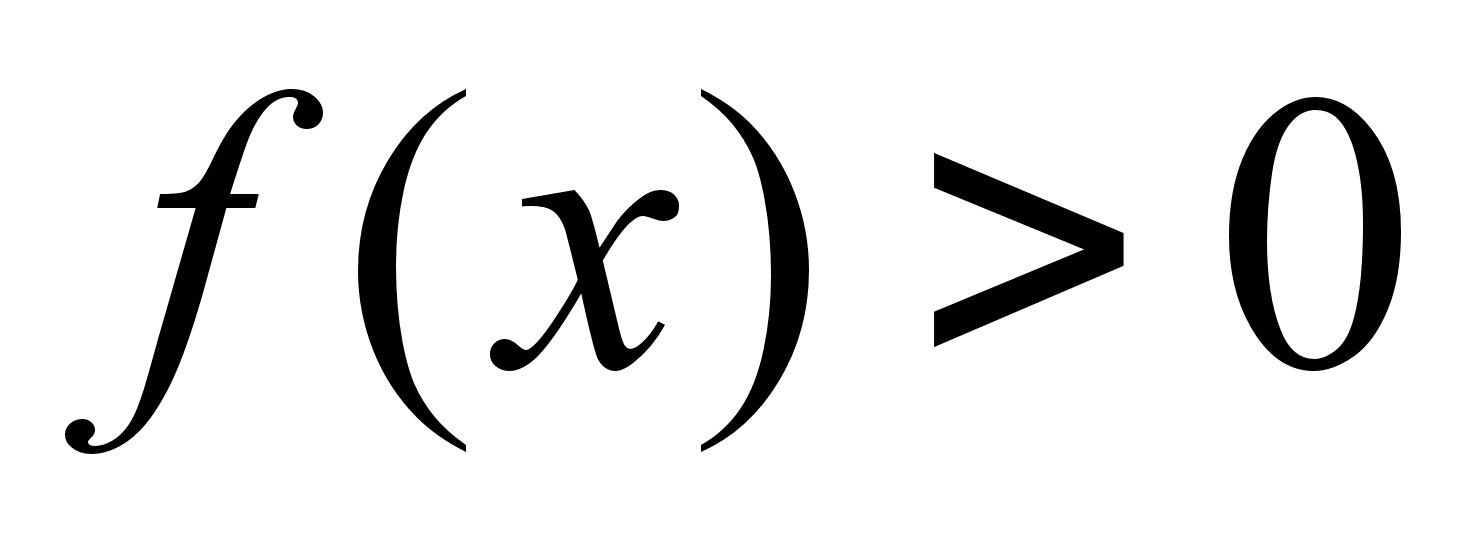 .
.
(использована
формула:
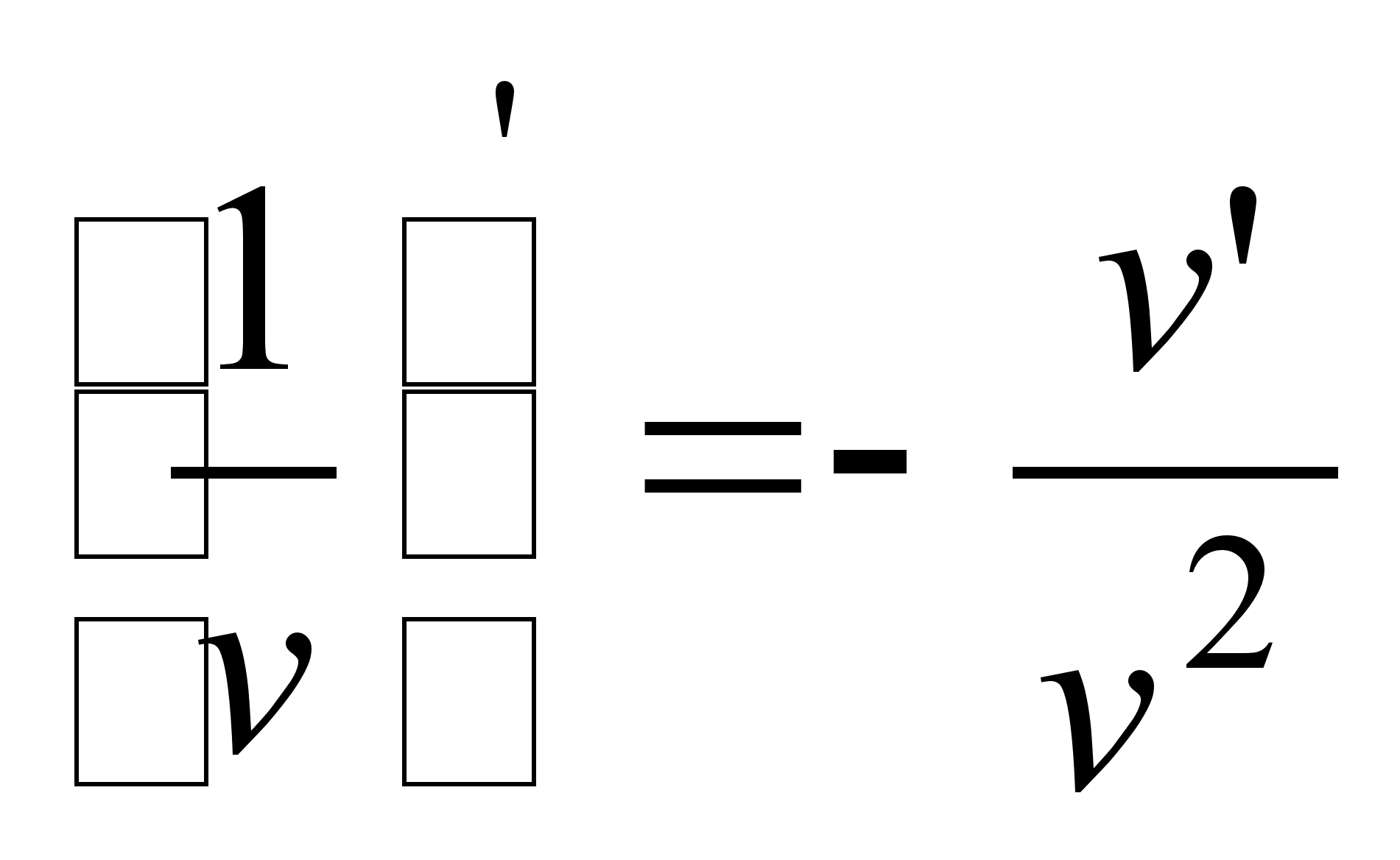 );
);
а)
нет критических
точек, где
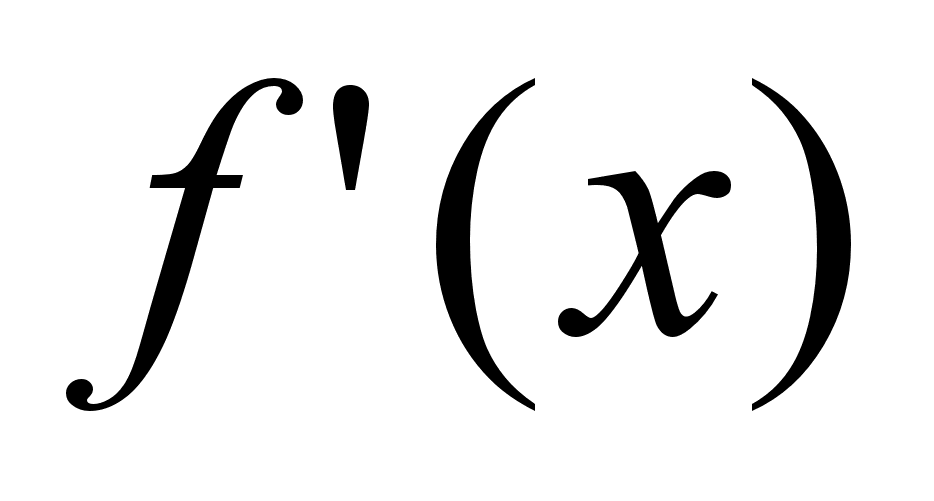 не существует,
т.к.
не существует,
т.к.
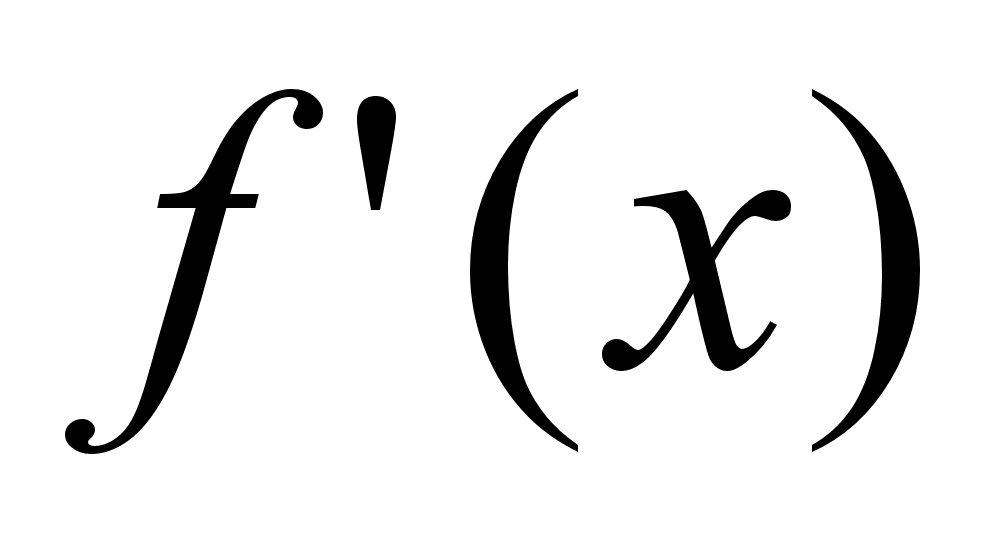 не имеет значе-
не имеет значе-
ния
только при
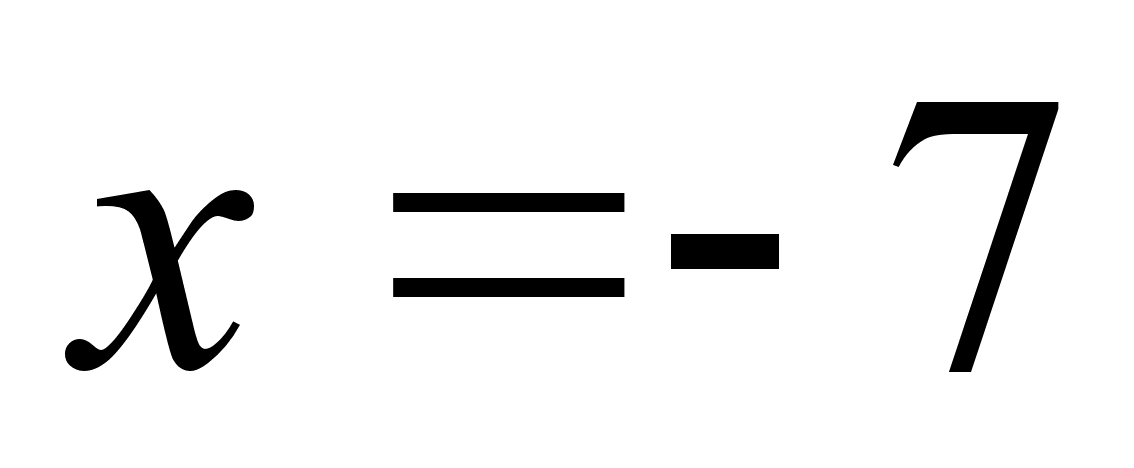 ,
но
,
но
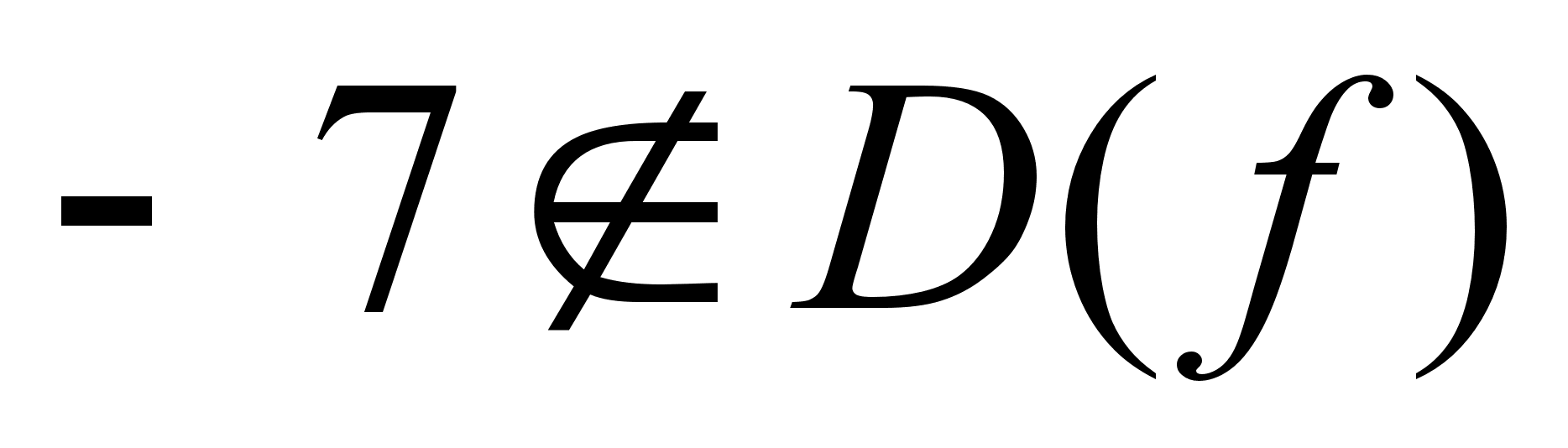 ;
;
б)
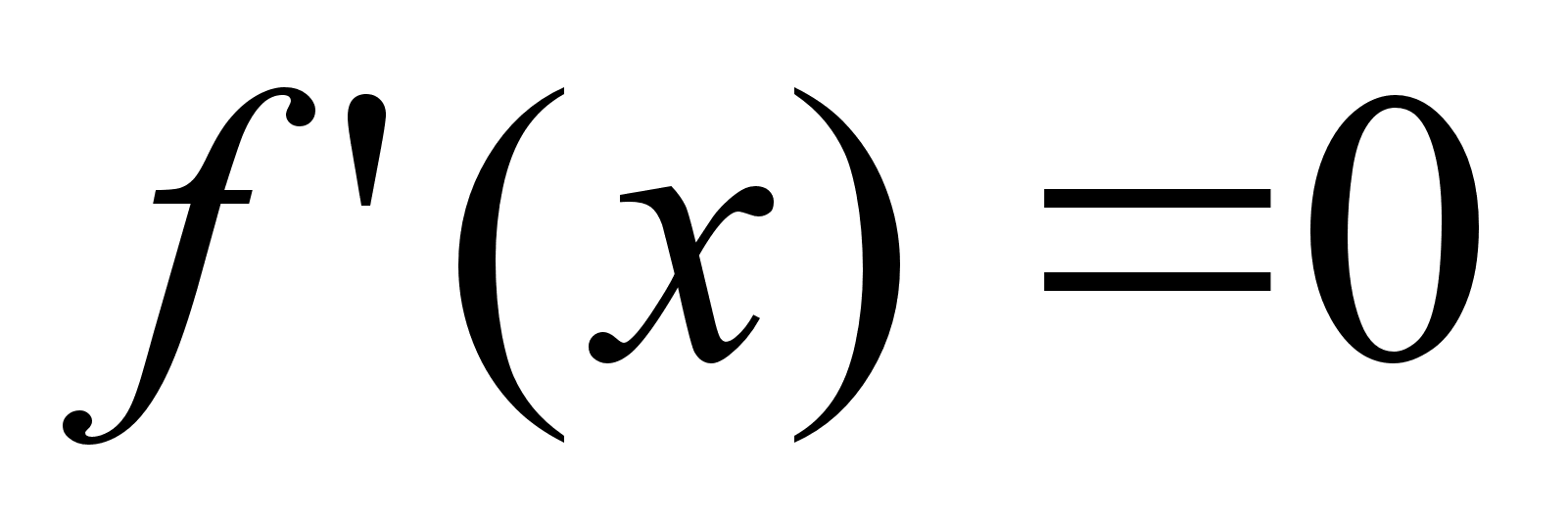 при
при
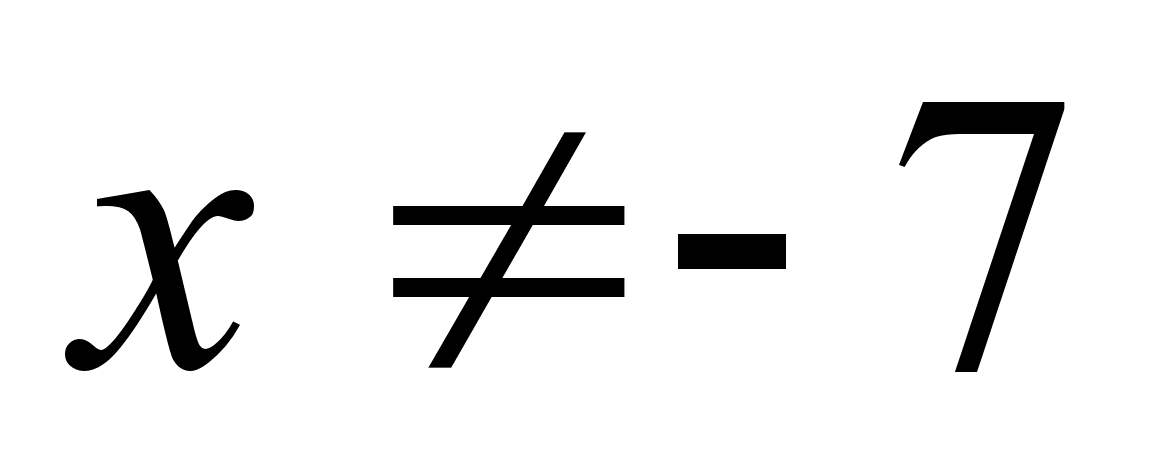 и
и
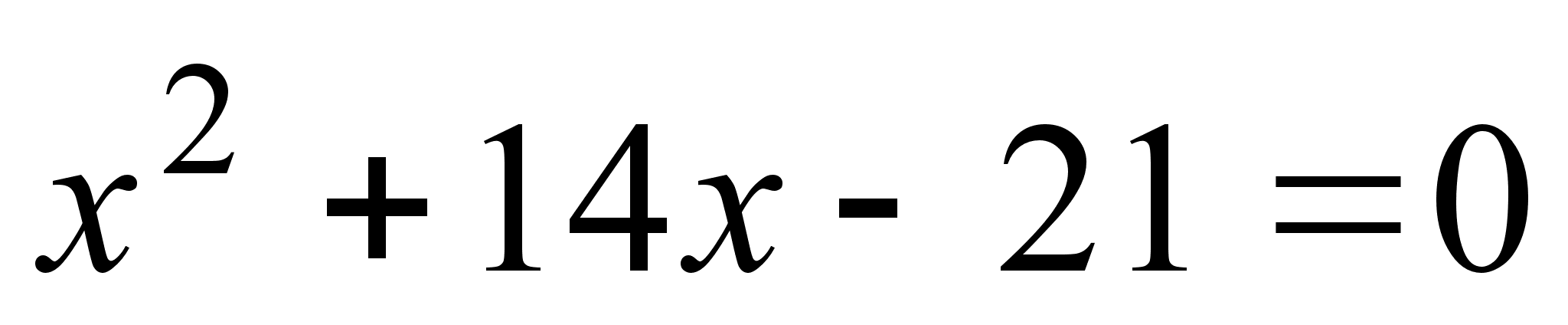 ,
т.е. при
,
т.е. при
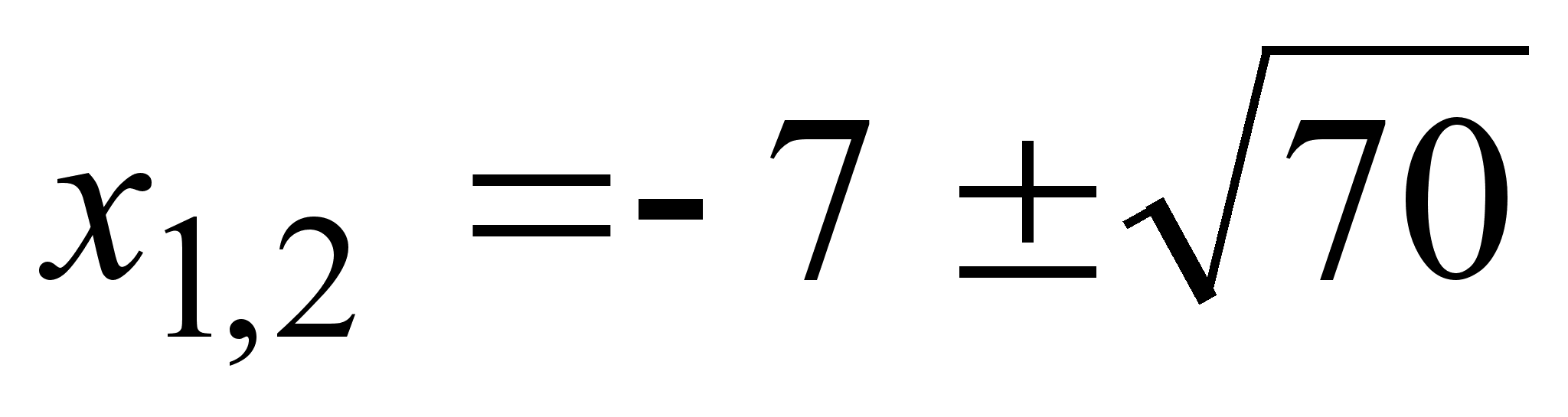 ;
;
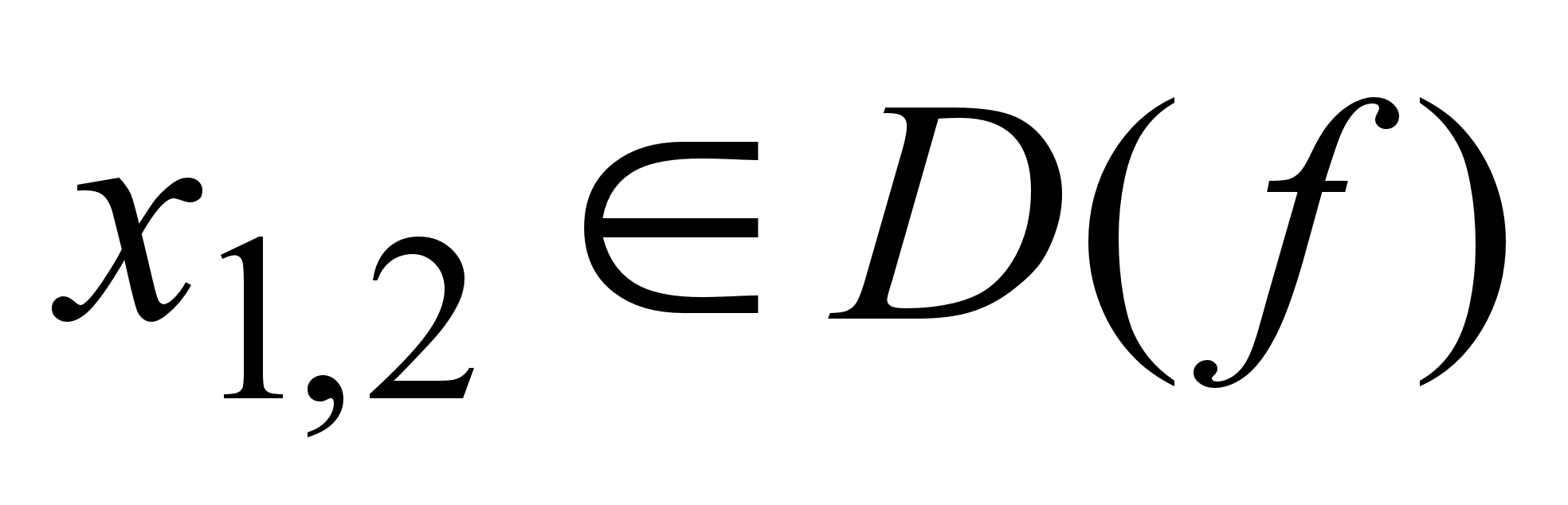 ;
;
значит,
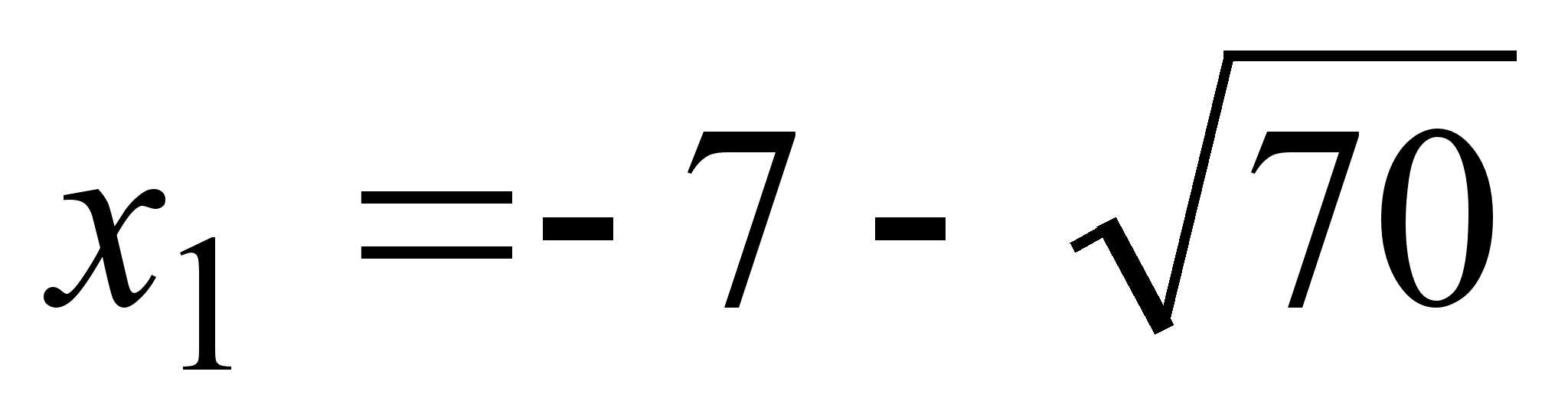 и
и
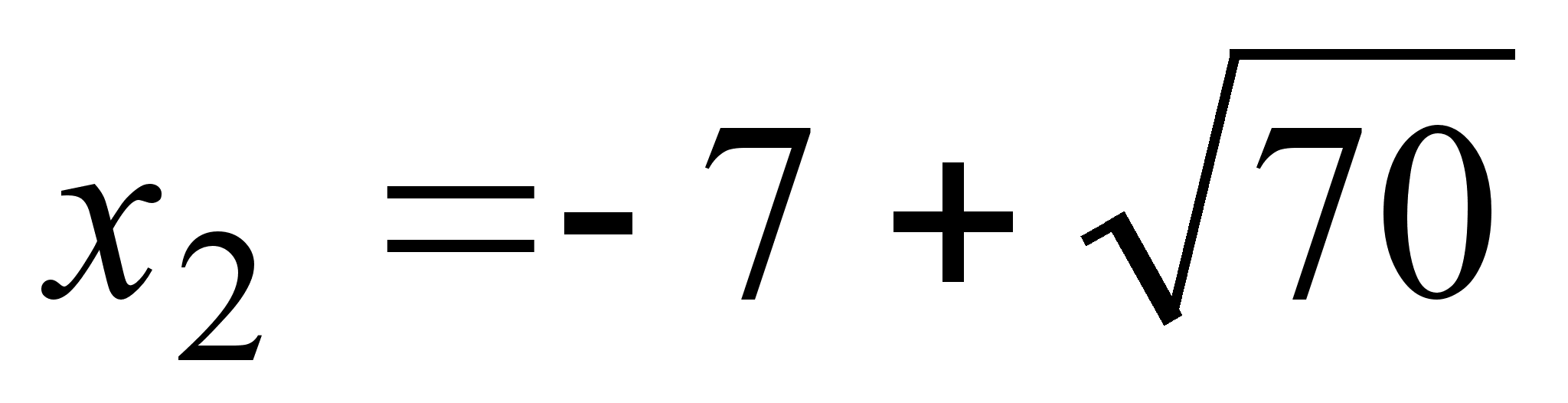 - критические
точки, а
- критические
точки, а
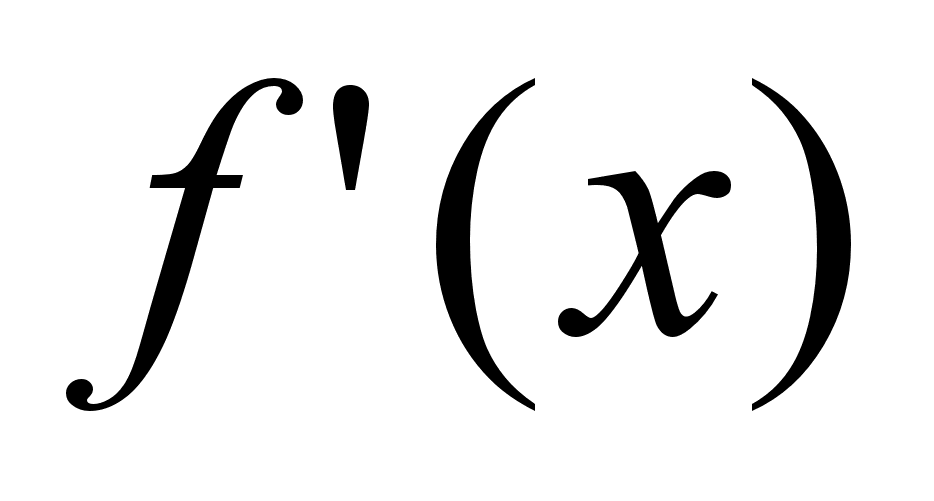
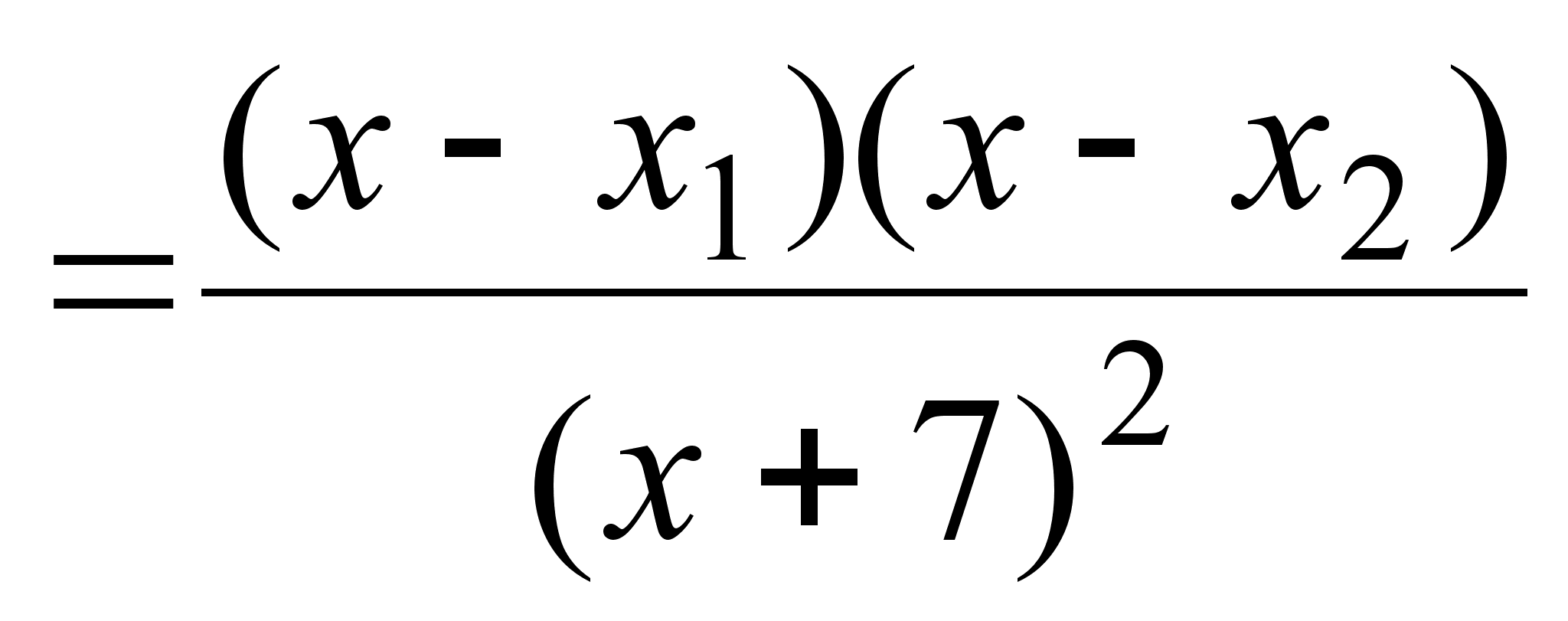 ;
;
 .
.
7)
|
|
|
|
|
|
|
|
|
|
|
|
+ | 0 | - | нет зн. | - | 0 | + | + |
|
|