Методичні вказівки до виконання розрахунко роботи дослідження за допомогою еом коливань системи з одним ступенем вільності
height="534" align="ABSMIDDLE" /> в рішенні при
при
 =5.0,861
= 4,31с:
=5.0,861
= 4,31с:
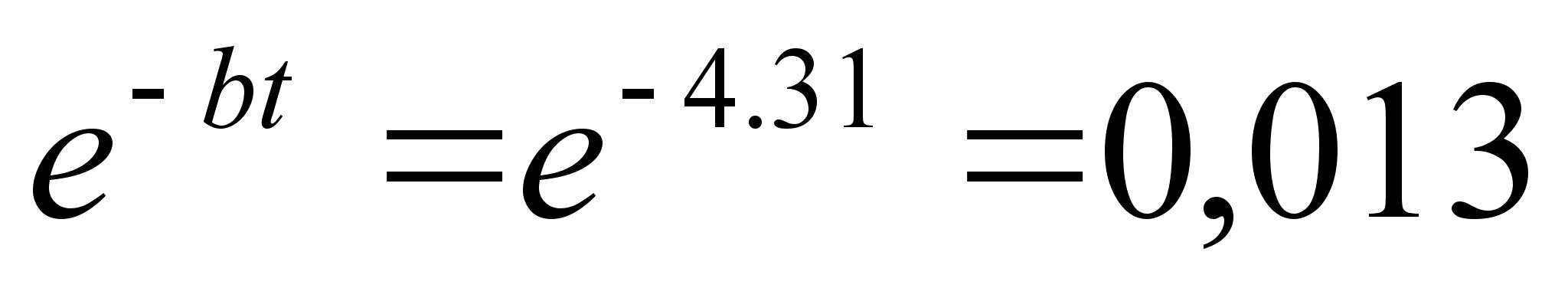 .
.
Таке
значення співмножника
(наближене до
нуля) в рішенні
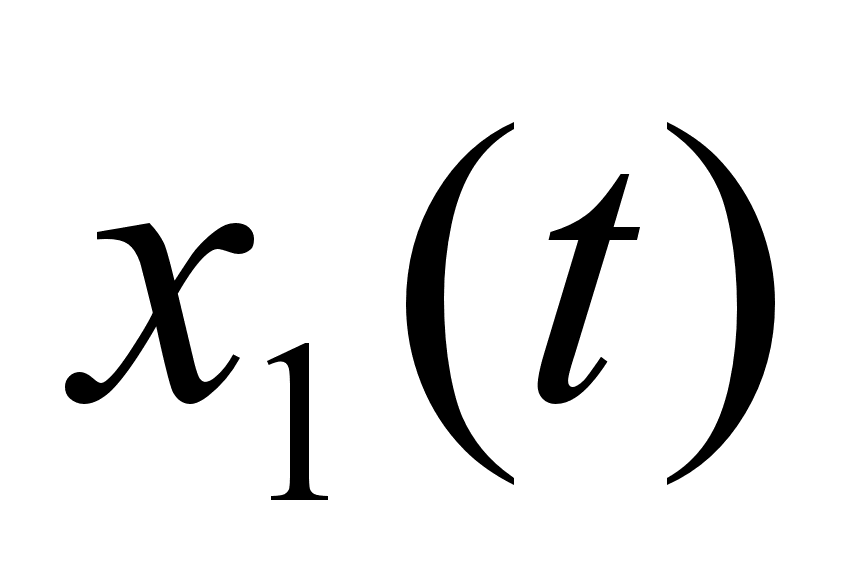 підтверджує
факт, що вільні
коливання
системи на цей
момент часу
практично
згасають; значить
коефіцієнт
підтверджує
факт, що вільні
коливання
системи на цей
момент часу
практично
згасають; значить
коефіцієнт
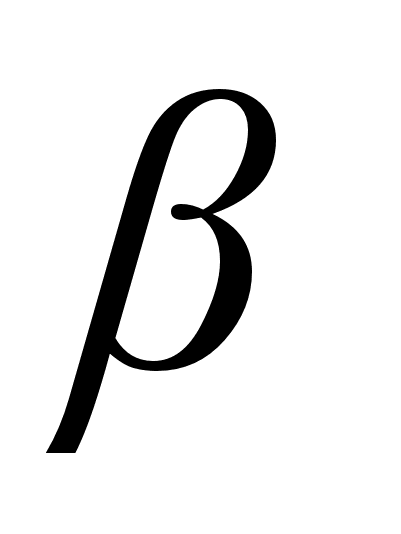 знайдено вірно.
знайдено вірно.
- Визначення амплітудних- та фазово-частотних характеристик системи.
Шляхом
виведення, за
допомогою ЕОМ,
для заданої
механічної
системи з
параметрами
 =
0,256т;
=
0,256т;
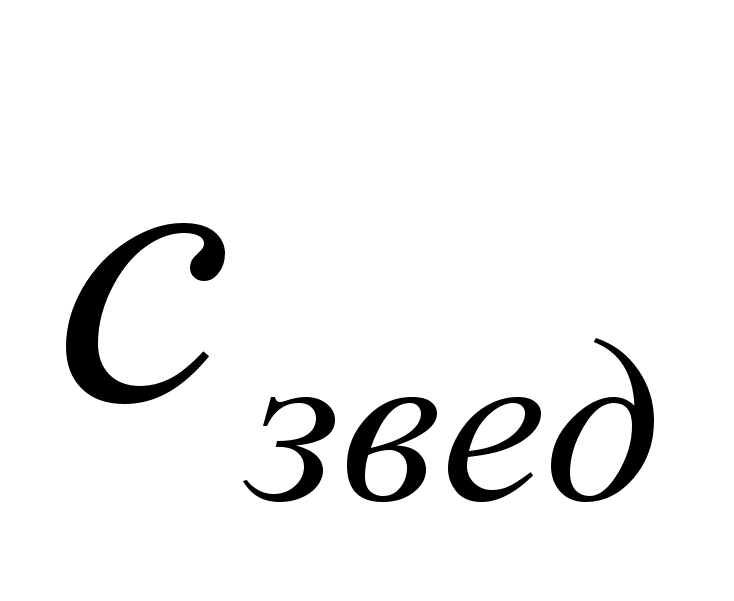 =
13,6кН.м
–1;
=
13,6кН.м
–1;
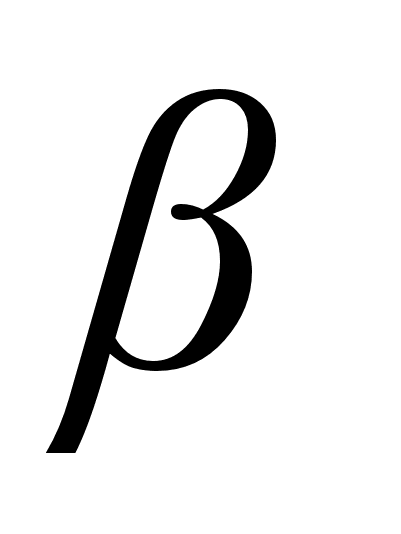 =
0,456кН.с.м–1
получимо (шляхом
введення на
друкарський
пристрій –
принтер) амплітудно-
та фазово-частотніх
характеристики
системи та
приведемо їх
на рис.2 і рис.3
(відповідно).
=
0,456кН.с.м–1
получимо (шляхом
введення на
друкарський
пристрій –
принтер) амплітудно-
та фазово-частотніх
характеристики
системи та
приведемо їх
на рис.2 і рис.3
(відповідно).
Розкладання функції F(t) в ряд Фур’є та визначення параметрів гармонік збурюючої сили.
Розкладемо
функцію
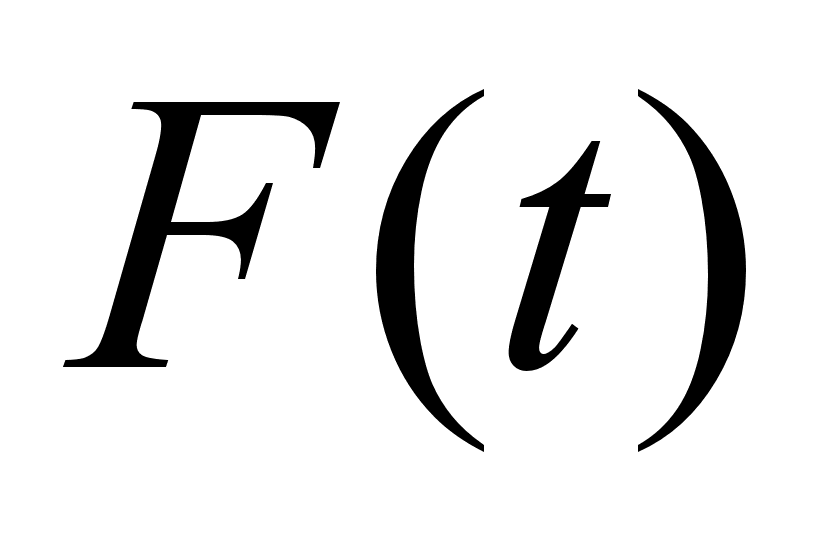 в ряд Фур’є:
в ряд Фур’є:
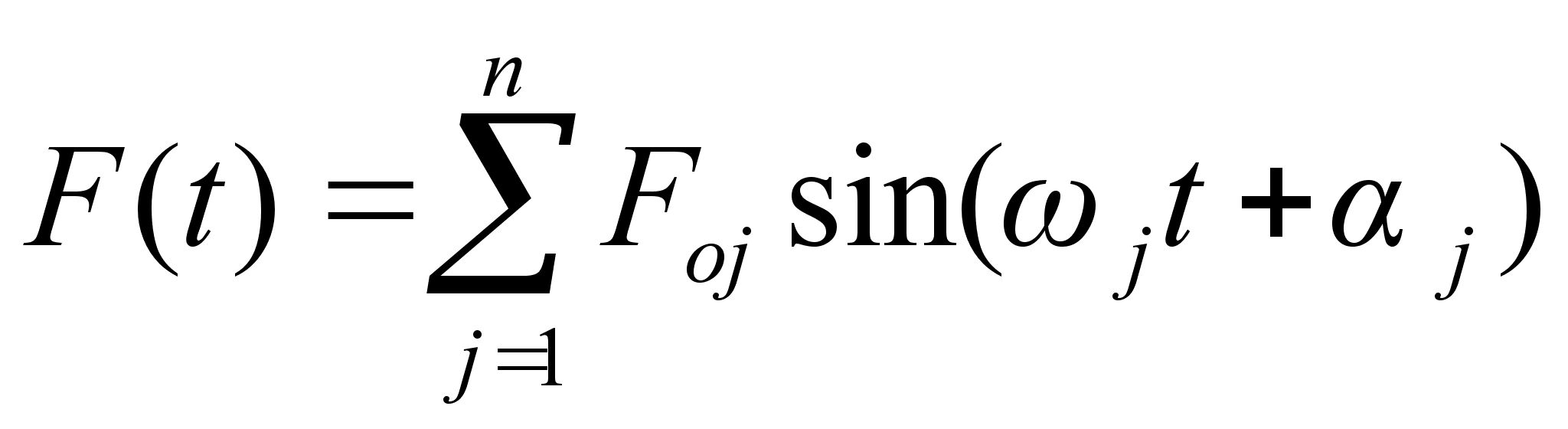 ,
( )
,
( )
де
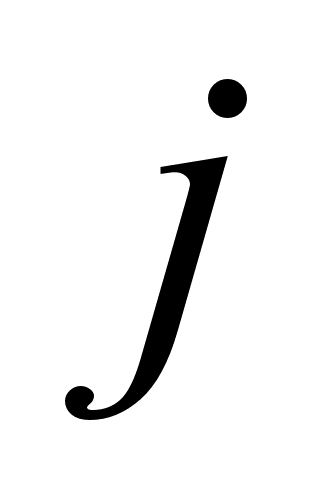 -
номер гармоніки,
а
-
номер гармоніки,
а
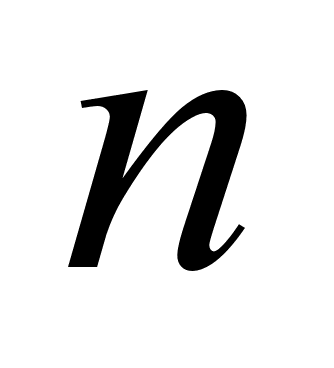 -
число гармонік
в розкладенні.
-
число гармонік
в розкладенні.
Визначимо
(за допомогою
ЕОМ) параметри
гармонік: амплітуди
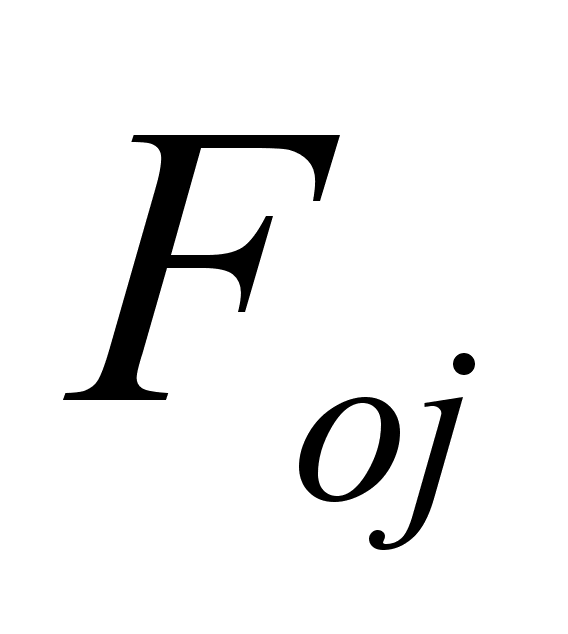 ,
частоти
,
частоти
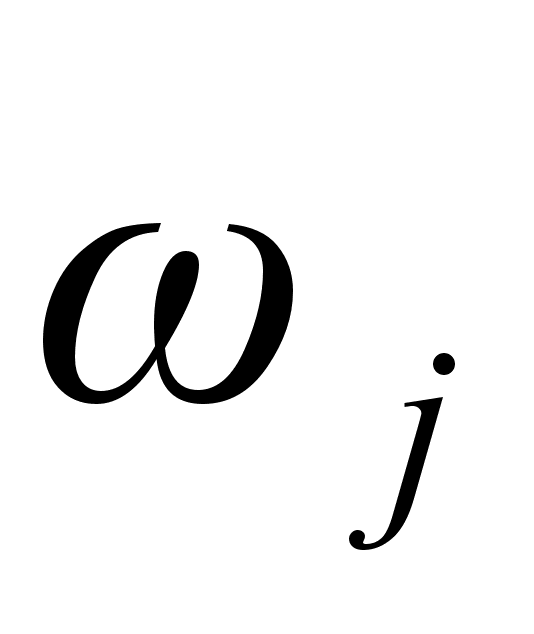 та
початкової
фази
та
початкової
фази
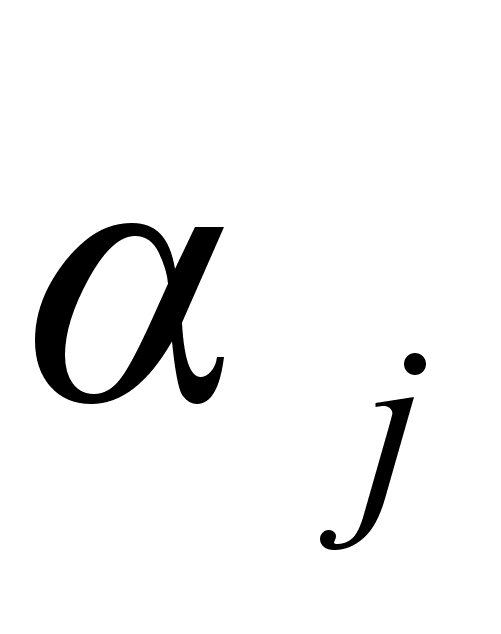 .
.
Для
заданої сили
“прямокутного”
типу з параметрами
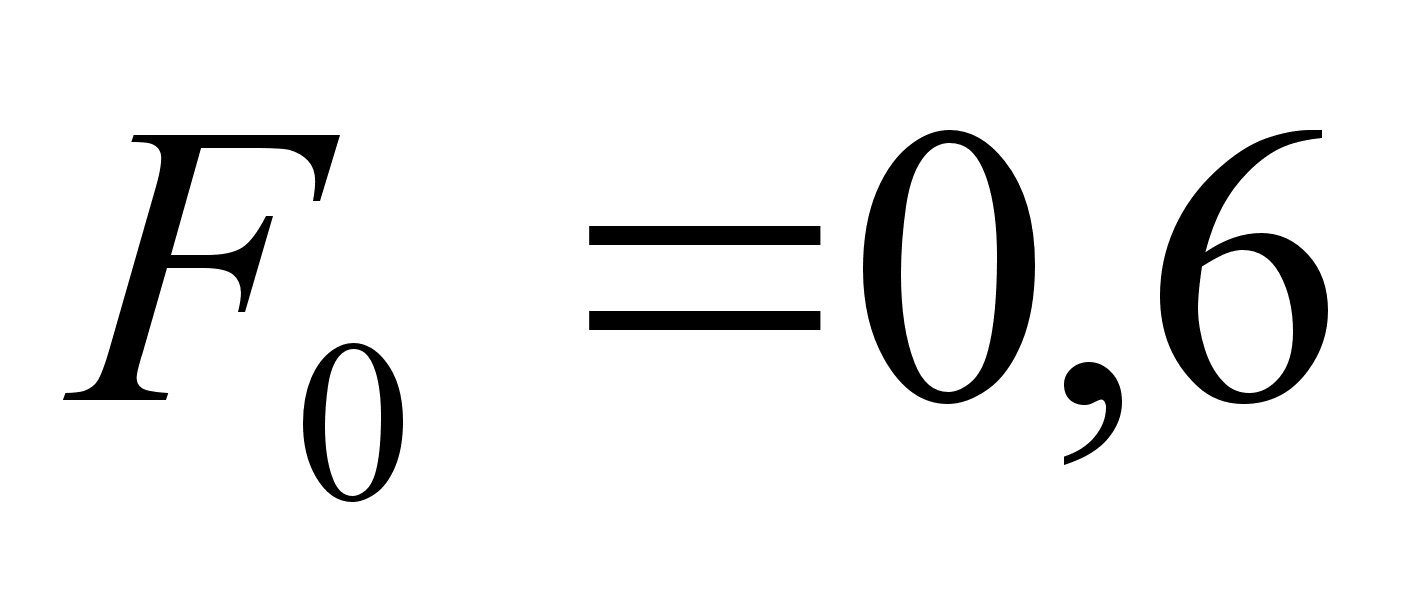 кН,
кН,
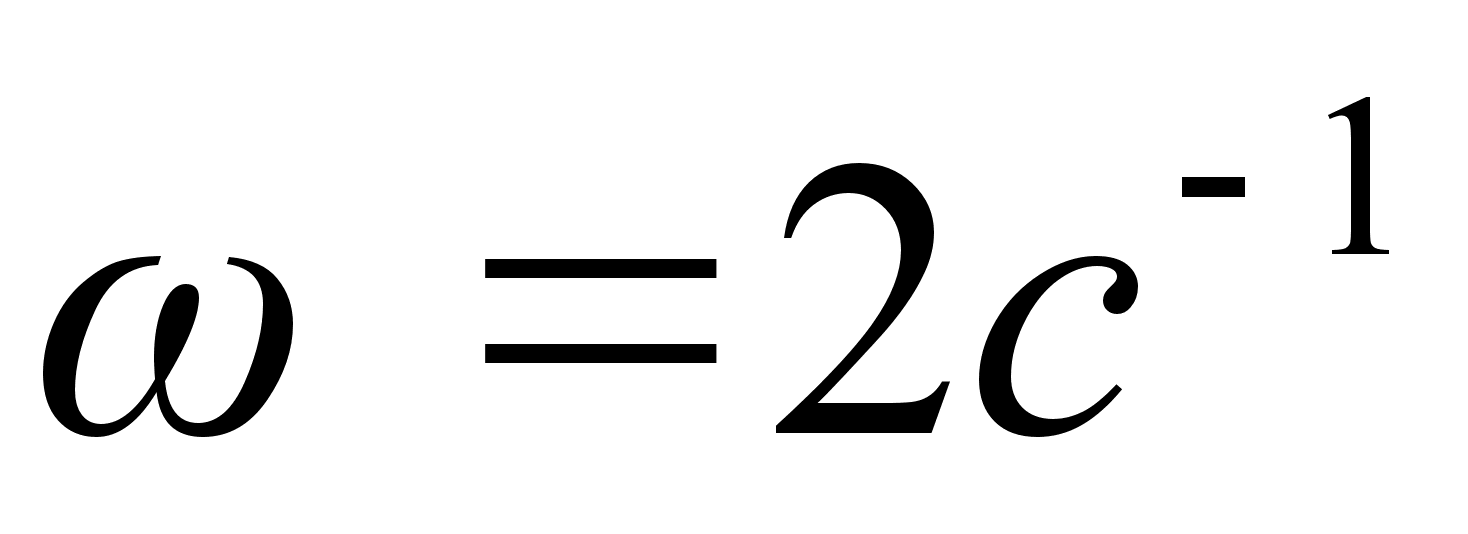 значення параметрів
гармонік наведені
у табл.1.
значення параметрів
гармонік наведені
у табл.1.
Таблиця 1.
|
Номер гармоніки,
|
кН |
|
рад. |
| 1 | 0,764 | 2 | 0 |
| 2 | 0,255 | 6 | 0 |
| 3 | 0,153 | 10 | 0 |
| 4 | 0,109 | 14 | 0 |
| 5 | 0,085 | 18 | 0 |
- Дослідження вимушених коливань механічної системи.
Визначення (за допомогою ЕОМ) “точного” рішення диференціального рівняння. Аналіз рішення.
Визначимо
за допомогою
ЕОМ “точне”
рішення
 диференціального
рівняння для
випадку, коли
сила
диференціального
рівняння для
випадку, коли
сила
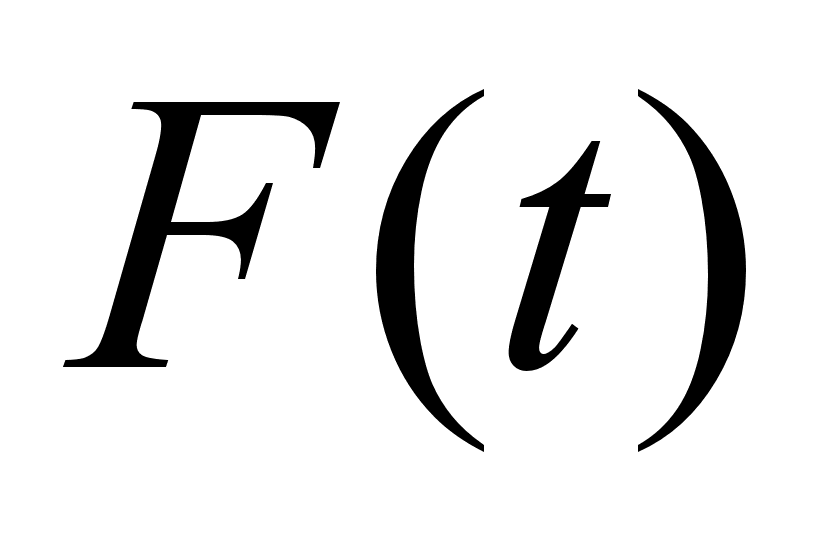 представлена
однією гармонікою
(
представлена
однією гармонікою
(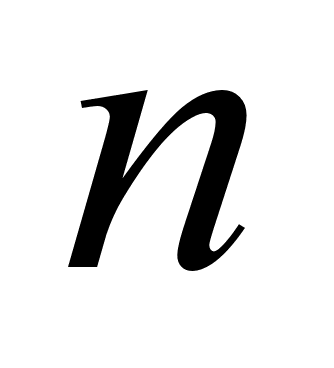 =1).
Два графіка
функцій
=1).
Два графіка
функцій
 для відповідних
випадків виводяться
на екран ЕОМ.
Перед виводом
графіків на
друкарський
пристрій їх
треба “промасштабувати”,
тобто получити
рішення на
заданому відрізку
інтегрування
0
для відповідних
випадків виводяться
на екран ЕОМ.
Перед виводом
графіків на
друкарський
пристрій їх
треба “промасштабувати”,
тобто получити
рішення на
заданому відрізку
інтегрування
0 ,
де
,
де
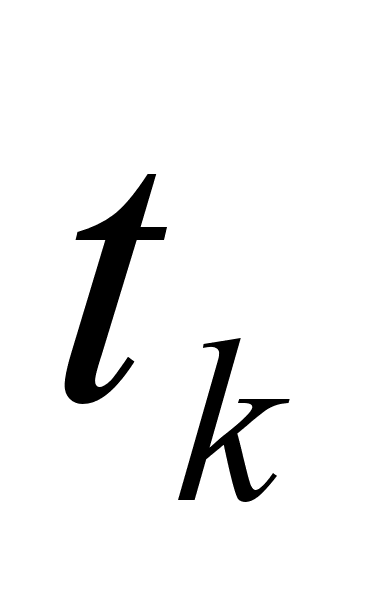 рекомендується
задавати рівним
8
рекомендується
задавати рівним
8 10
10 .
На рис.4 приведені
вказані графіки
функцій
.
На рис.4 приведені
вказані графіки
функцій
 для заданої
механічної
системи. Лінія
1 відображає
“точне” рішення,
а лінія 2 – рішення
у випадку
для заданої
механічної
системи. Лінія
1 відображає
“точне” рішення,
а лінія 2 – рішення
у випадку
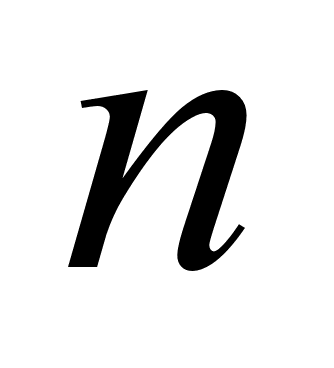 =
1 (тобто, коли
=
1 (тобто, коли
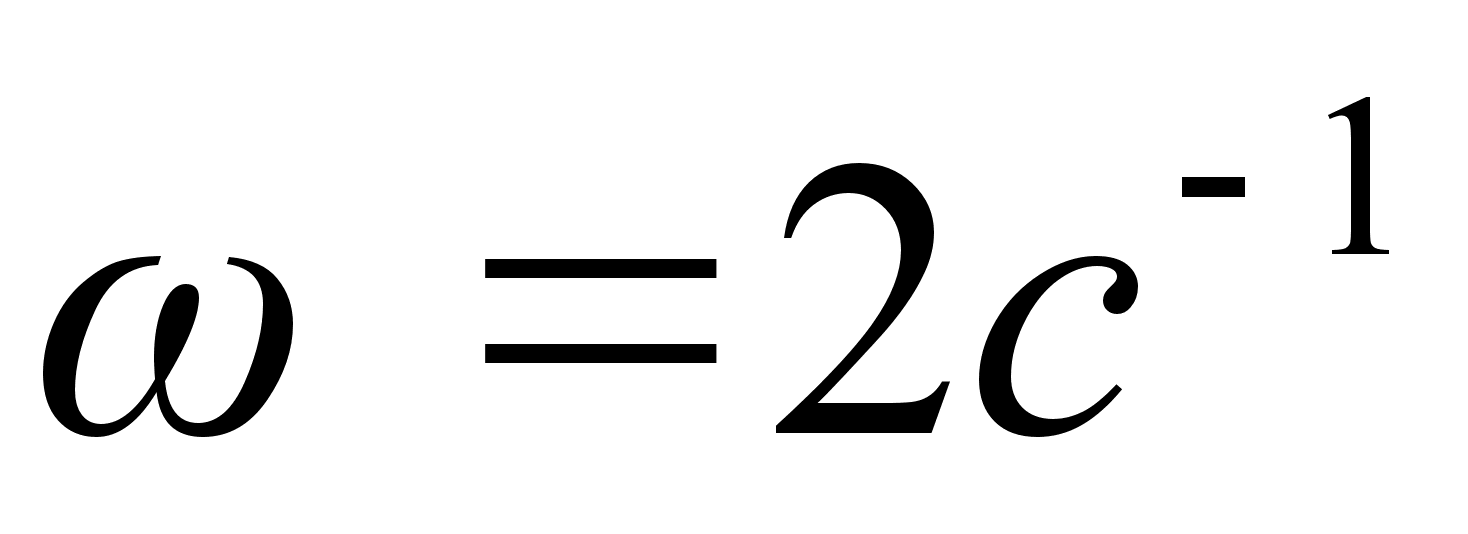 ).
).
Із
графіків видно,
що функції
 получаються
періодичними,
тобто рух механічної
системи получається
періодичним-коливальним.
І в першому, і
в другому випадку
при
получаються
періодичними,
тобто рух механічної
системи получається
періодичним-коливальним.
І в першому, і
в другому випадку
при
 с
процеси получилися
явно усталеними,
тобто без вільних
коливань. Але
в “точному”
рішенні навіть
при
с
процеси получилися
явно усталеними,
тобто без вільних
коливань. Але
в “точному”
рішенні навіть
при
 явно виражені
дві частоти
– одна дорівнює
явно виражені
дві частоти
– одна дорівнює
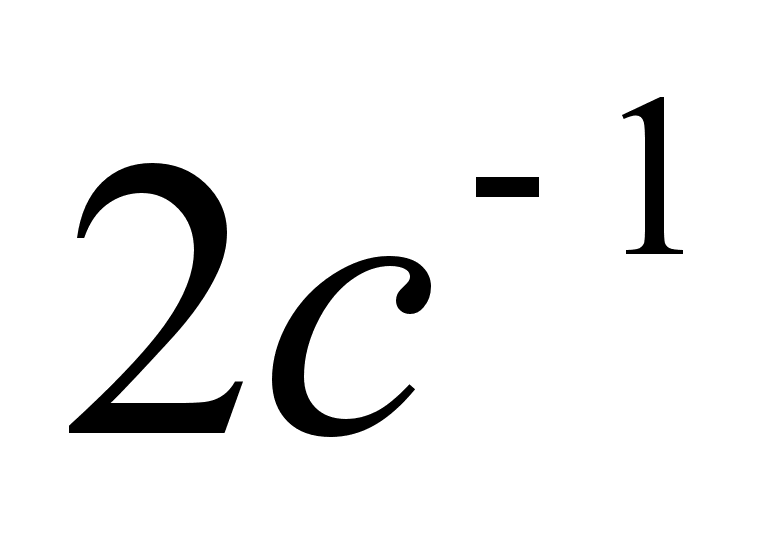 (див. лінію 2 для
випадку
(див. лінію 2 для
випадку
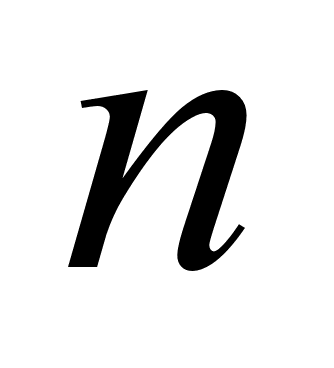 =
1; це частота
першої гармоніки),
а друга частота
– втричі більша
(це частота
другої гармоніки,
див. табл. 1). Рішення,
що відповідають
лініям 1 і 2, значно
відрізняються
одне від одного.
Наприклад, в
момент часу
=
1; це частота
першої гармоніки),
а друга частота
– втричі більша
(це частота
другої гармоніки,
див. табл. 1). Рішення,
що відповідають
лініям 1 і 2, значно
відрізняються
одне від одного.
Наприклад, в
момент часу
 с
(
с
( =4,31с)
значення
=4,31с)
значення
 м
(точне рішення)
і
м
(точне рішення)
і
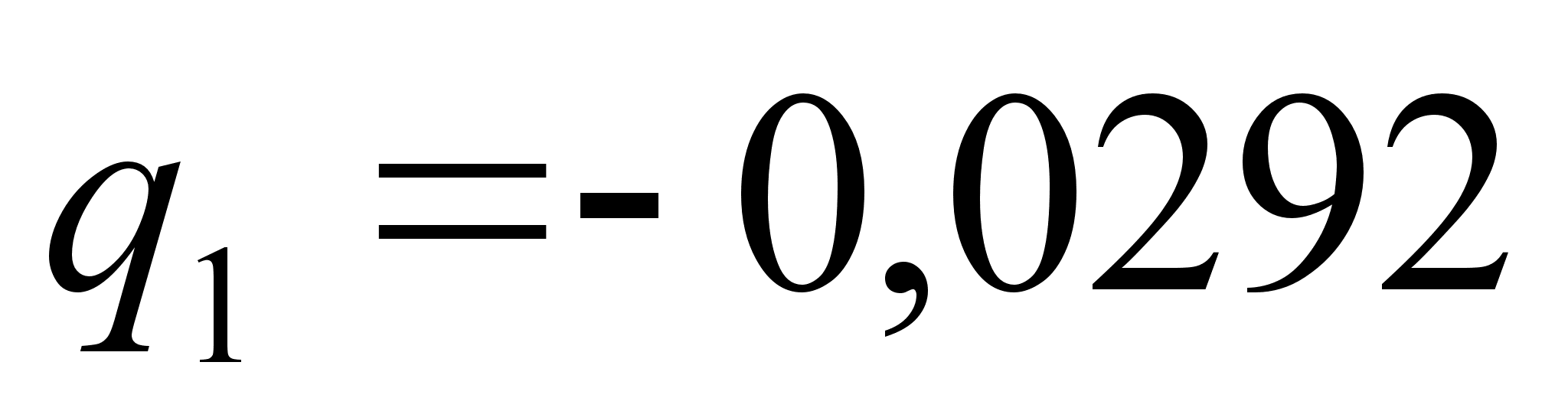 м
(випадок
м
(випадок
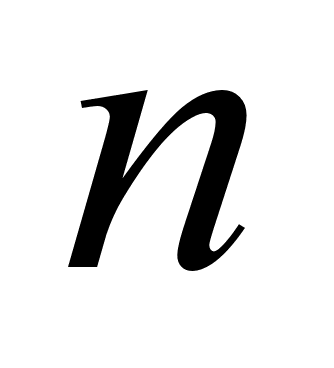 =
1).
=
1).
Підбір (за допомогою ЕОМ) раціональної кількості гармонік
 в розкладанні
функції
в розкладанні
функції
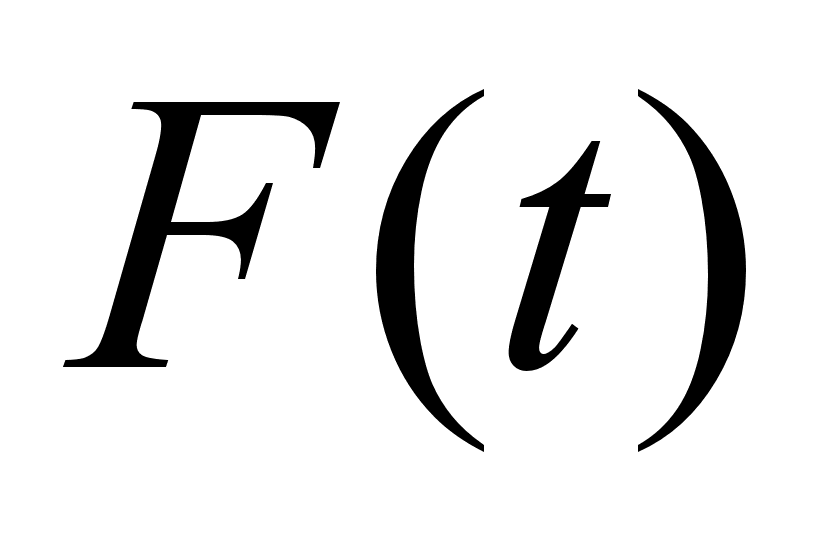 .
.
Визначимо
(за допомогою
ЕОМ) функції
 для випадків
для випадків
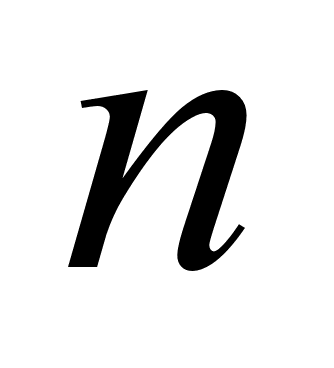 =
2, 3. На рис. 5, а, б
лініями 1 показані
графіки
=
2, 3. На рис. 5, а, б
лініями 1 показані
графіки
 для “точного”
рішення, а лініями
2 – графіки тих
же функцій для
випадків
для “точного”
рішення, а лініями
2 – графіки тих
же функцій для
випадків
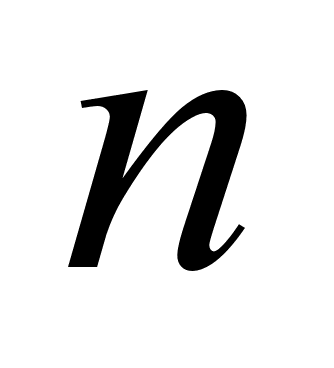 =
2;
=
2;
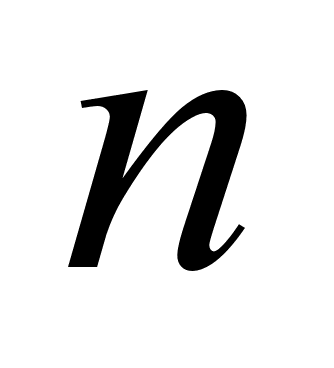 =
3 (відповідно).
Із рисунків
випливає, що
при
=
3 (відповідно).
Із рисунків
випливає, що
при
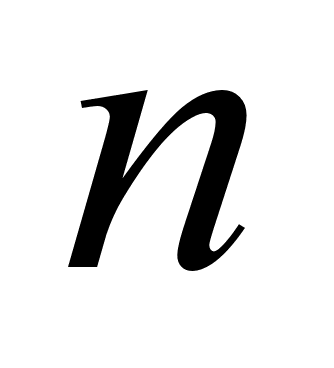 =
2 графік відрізняється
від “точного”
рішення, але
в значно меншій
степені, ніж
при
=
2 графік відрізняється
від “точного”
рішення, але
в значно меншій
степені, ніж
при
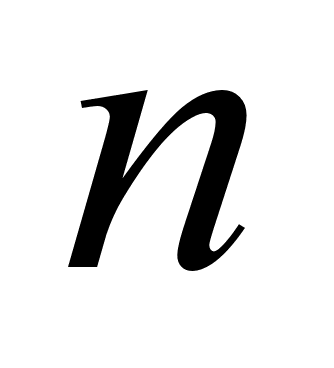 =
1. А у випадку
=
1. А у випадку
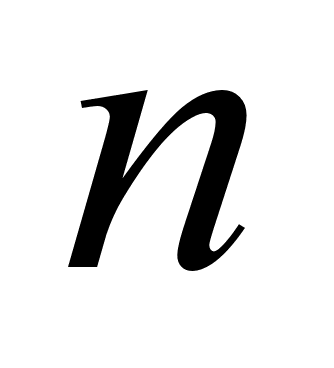 =
3 графік
=
3 графік
 практично не
відрізняється
від “точного”
рішення.
практично не
відрізняється
від “точного”
рішення.
Значення
відповідних
функції при
 с
становлять
с
становлять
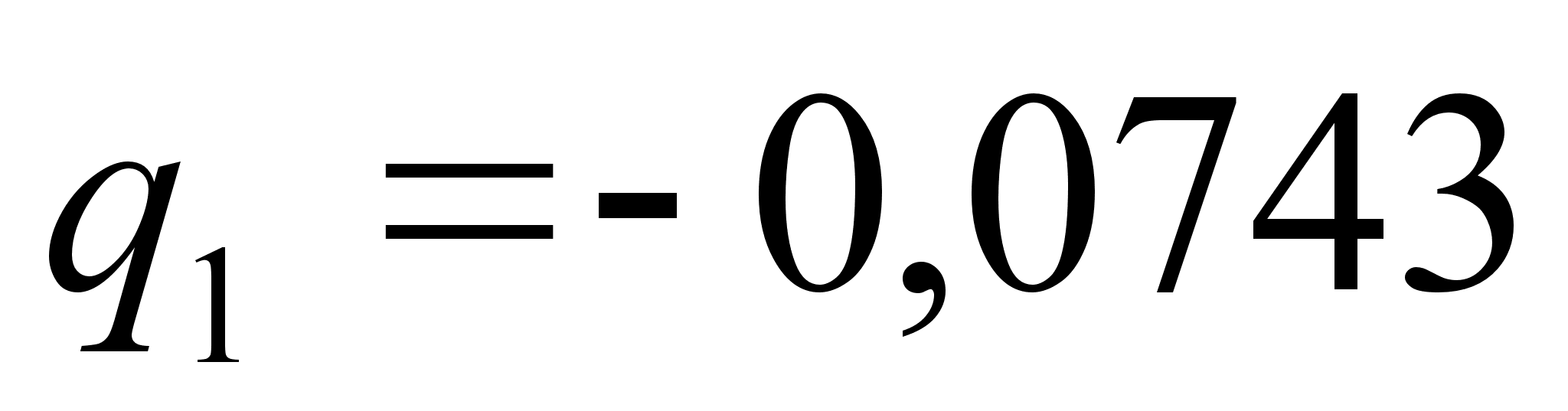 м
(
м
(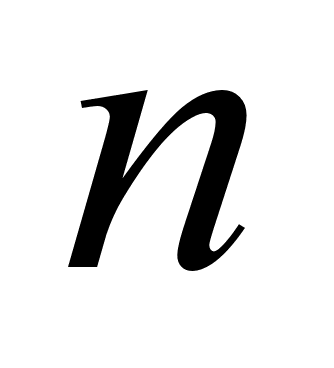 =
2) і
=
2) і
 м
(
м
(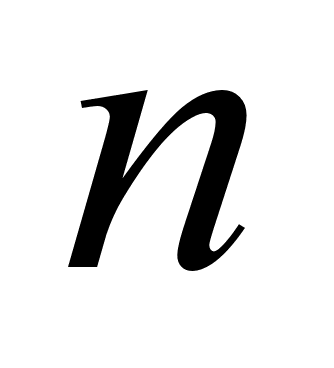 =
3), тобто при
=
3), тобто при
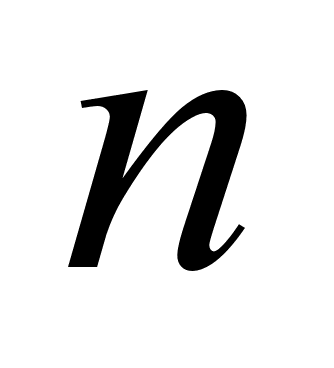 =
2 різниця в значеннях
відповідає
= 5,7%, а при
=
2 різниця в значеннях
відповідає
= 5,7%, а при
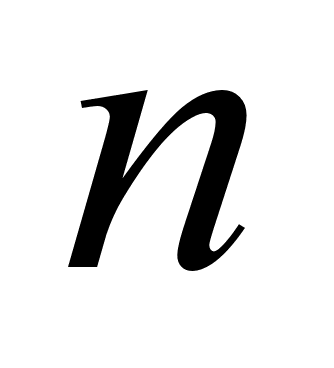 =
3 -
= 3,7%.
=
3 -
= 3,7%.
За
одержаним
результатам
можна зробити
висновок, що
для отримання
рішення
 з 5% точністю
достатньо взяти
кількість
гармонік
з 5% точністю
достатньо взяти
кількість
гармонік
 =
3 в розкладенні
збурюючої
сили
=
3 в розкладенні
збурюючої
сили
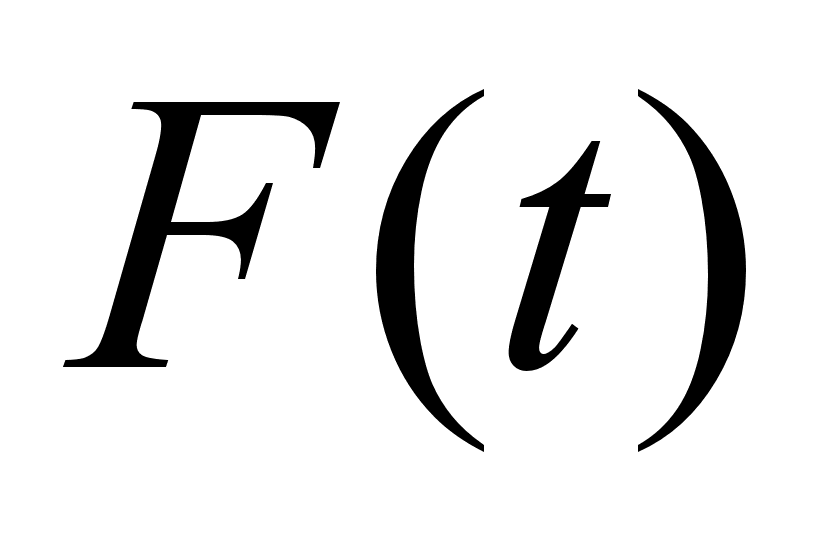 в ряд Фур’є.
в ряд Фур’є.
Побудова аналітичного рішення диференціального рівняння. Підбірраціональної кількості гармонік
 в розкладанні
функції
в розкладанні
функції
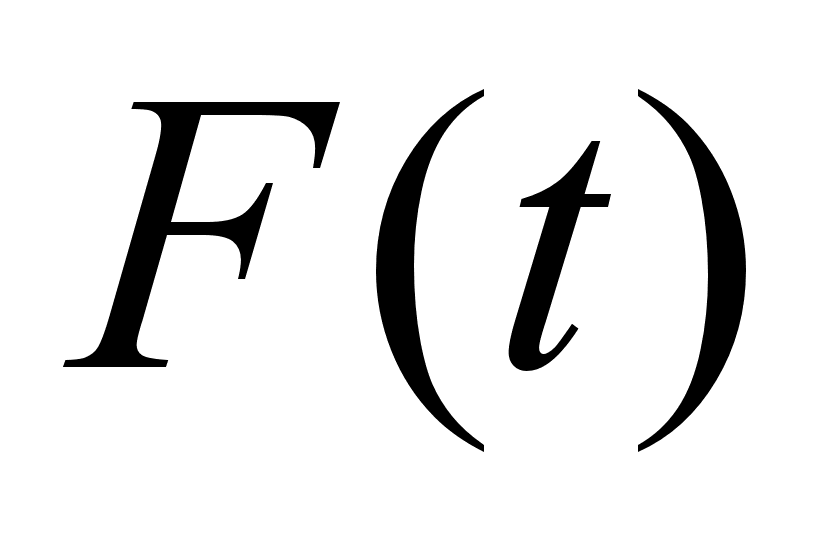 .
.
Побудуємо
аналітичне
рішення диференціального
рівняння ( ),
представивши
збурюючу силу
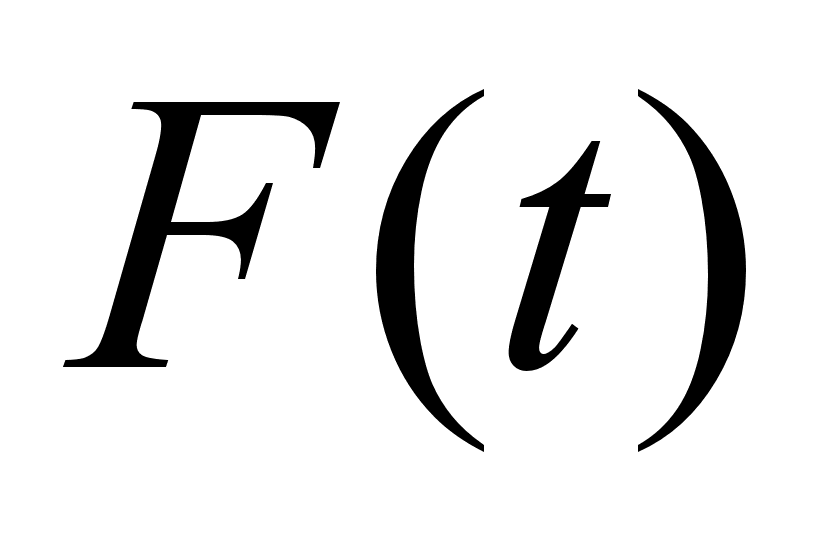 розкладенням
в ряд Фур’є:
розкладенням
в ряд Фур’є:
 .
.
Врахуемо,
що при
 рішення
рішення
 практично
згасає. Тоді
для цих моментів
часу:
практично
згасає. Тоді
для цих моментів
часу:
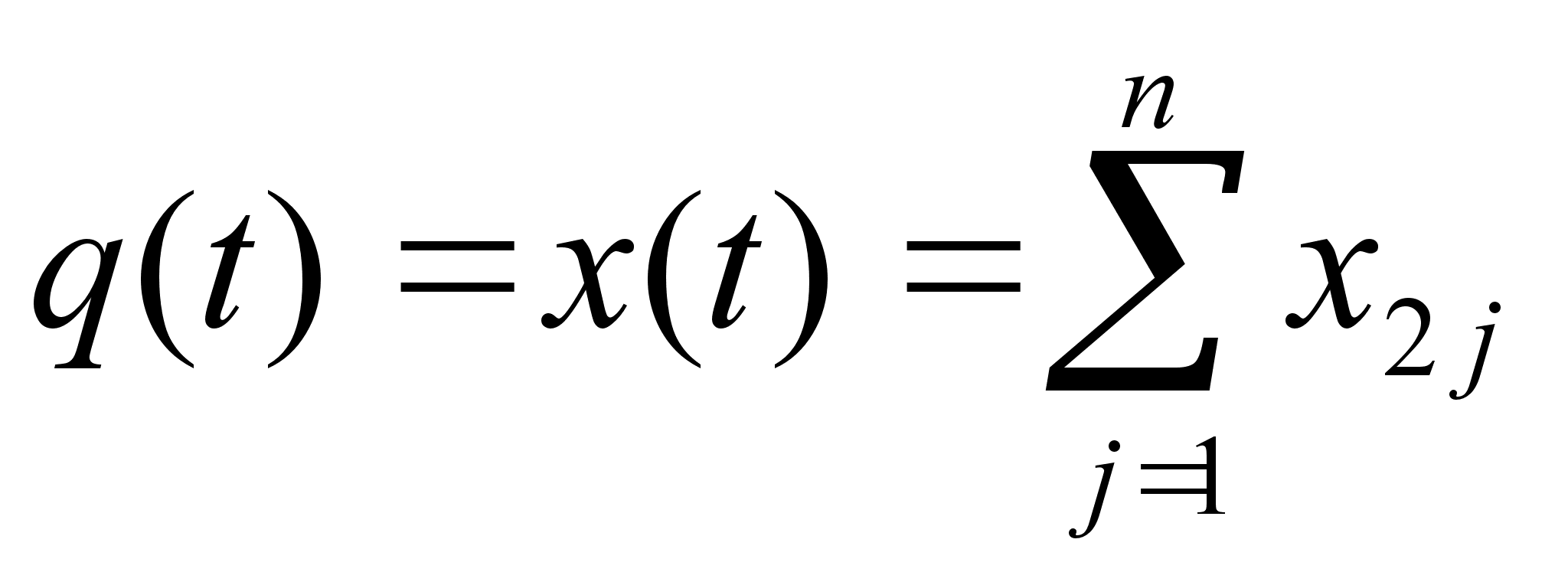 =
=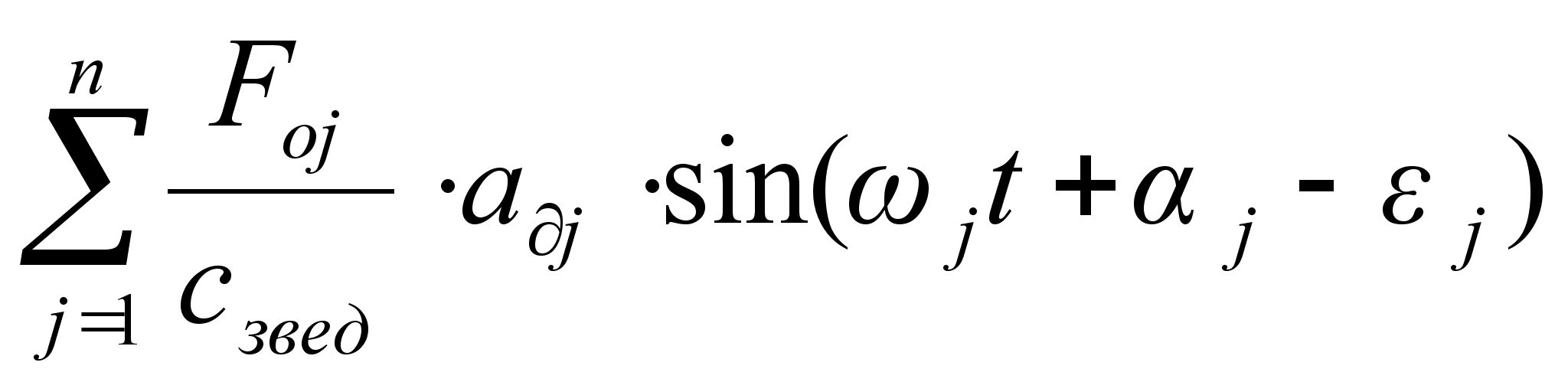 . (
).
. (
).
Відмітимо,
що рішення
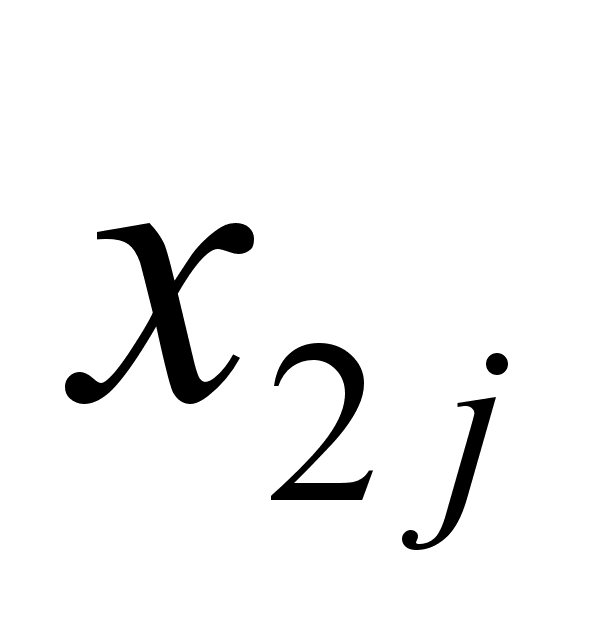 змінюється
з частотою
змінюється
з частотою
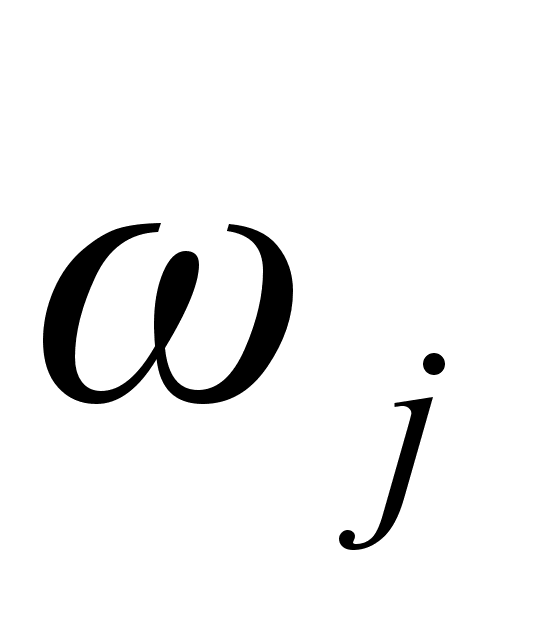 ,
яка є частотою
відповідної
гармоніки
збурюючої сили.
,
яка є частотою
відповідної
гармоніки
збурюючої сили.
Користуючись
даними табл.
1 та графіками
АЧХ і ФЧХ системи,
визначимо
значення коефіцієнта
динамічності
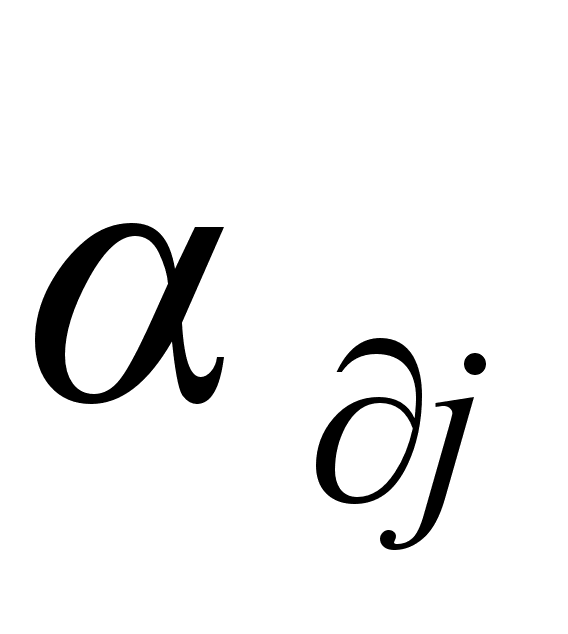 та зсуву фаз
та зсуву фаз
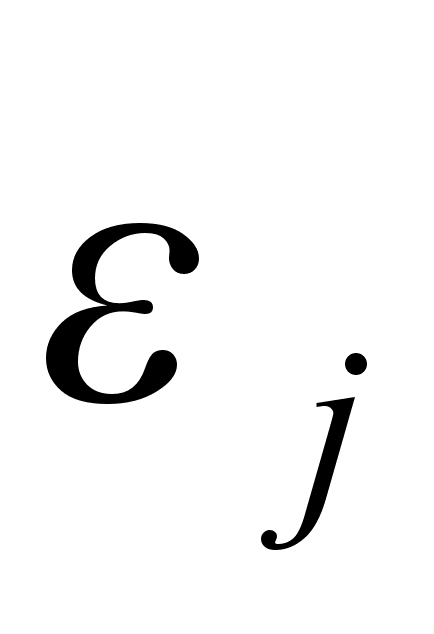 для
для
гармонік
( ),
а також амплітуди
коливань механічної
системи
),
а також амплітуди
коливань механічної
системи
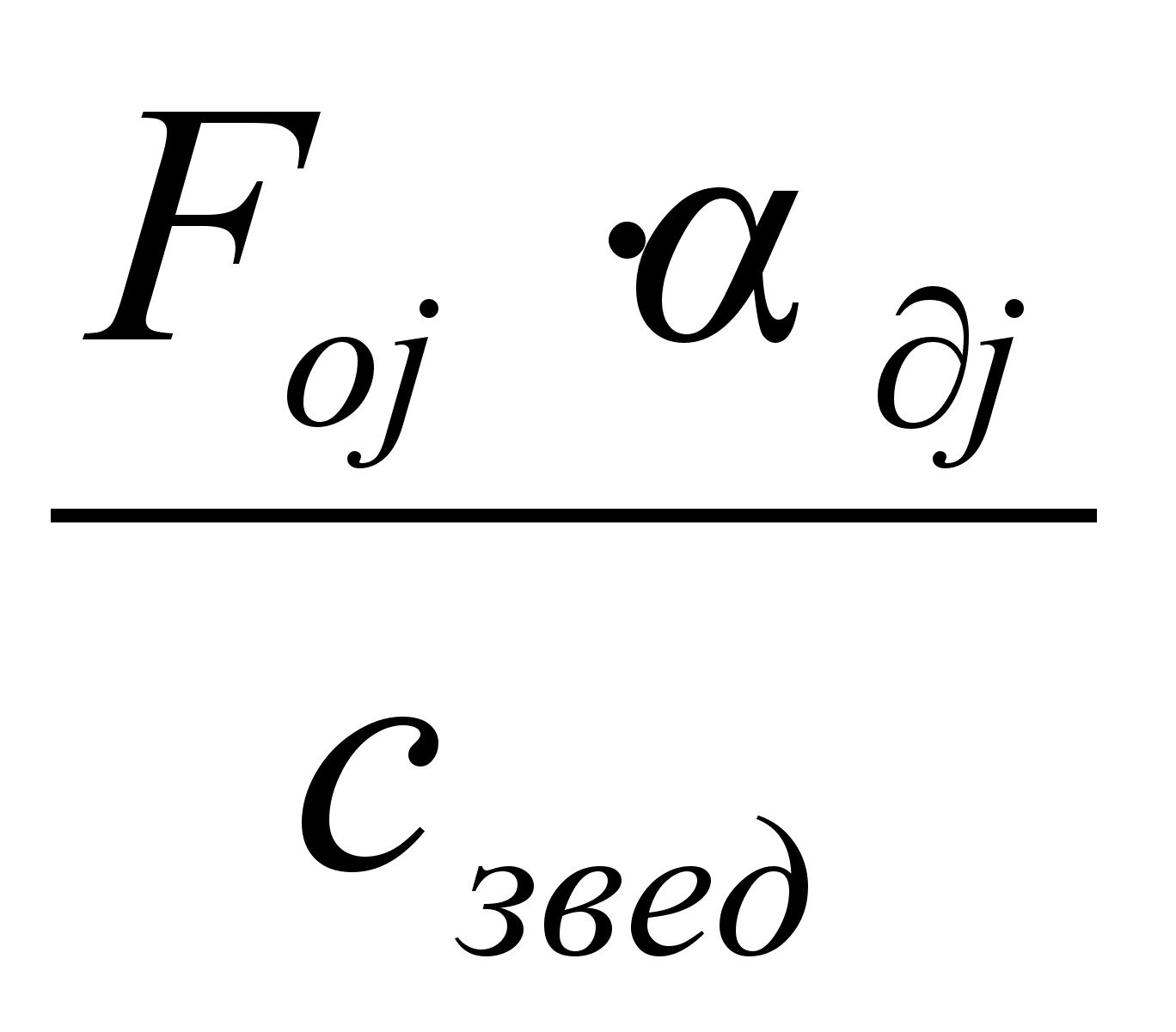 ,
що відповідають
цим гармонікам.
,
що відповідають
цим гармонікам.
Значення знайдених величин зведемо у табл. 2.
Таблиця 2.
|
Номер
гармоніки,
|
|
|
|
|
|
|
| 1 | 2 | 0,274 | 1,08 | 0,0562 | 0,0607 | 0,088 |
| 2 | 6 | 0,823 | 2,63 | 0,0188 | 0,0497 | 0,076 |
| 3 | 10 | 1,37 | 1,06 | 0,0113 | 0,012 | 3,09 |
| 4 | 14 | 1,92 | 0,366 | 0,008 | 0,0029 | 3,09 |
| 5 | 18 | 2,47 | 0,195 | 0,006 |
0,0012 |
3,09 |
Із
табл. 2 випливає,
що визначальними
є амплітуди
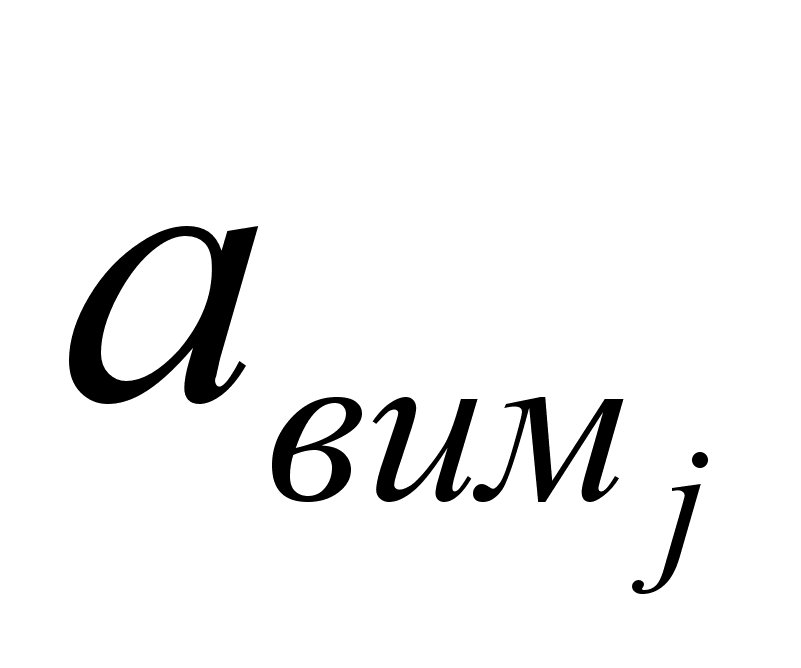 коливань
першої (
коливань
першої (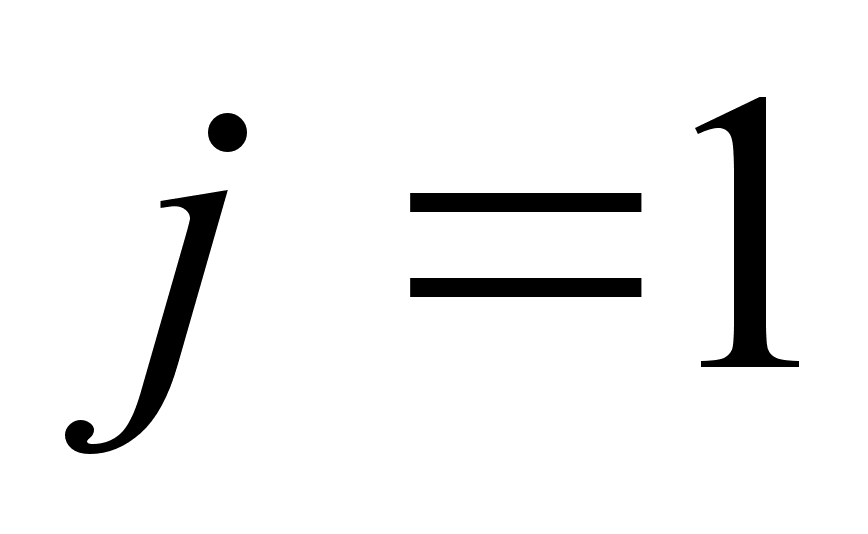 )
та другої (
)
та другої (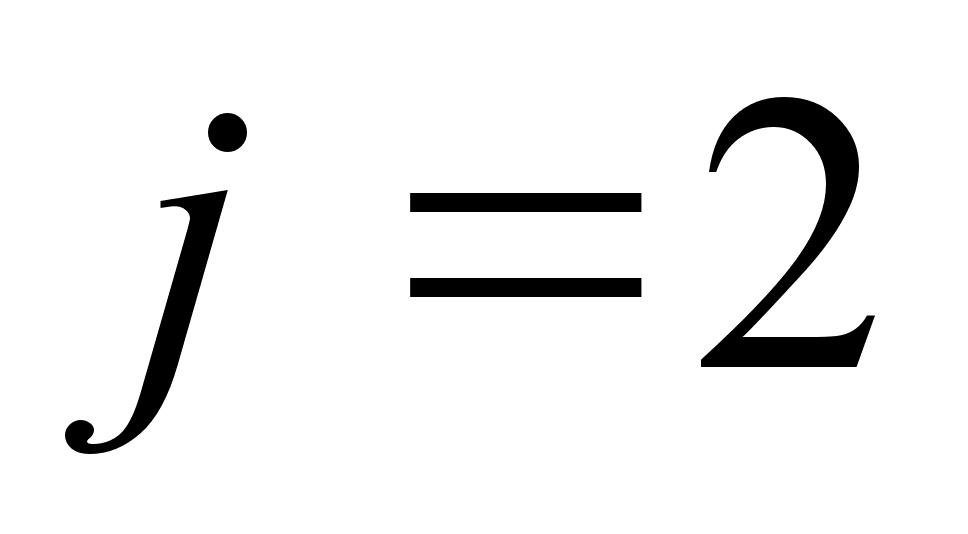 )
гармоніки в
рішенні
)
гармоніки в
рішенні
 ,
значення цих
амплітуд одного
порядку; амплітуди
третьої гармоніки
(
,
значення цих
амплітуд одного
порядку; амплітуди
третьої гармоніки
(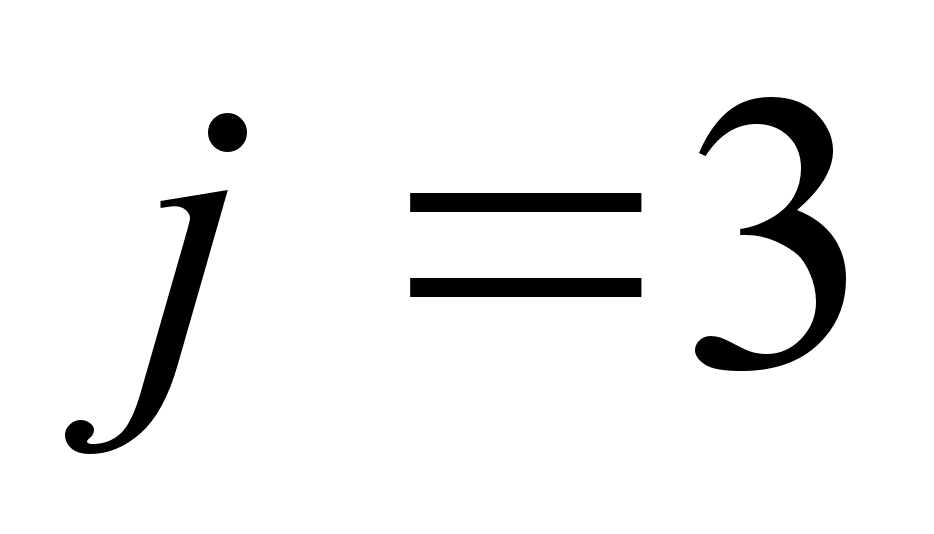 )
майже в 6 разів
менша, а четверта
(
)
майже в 6 разів
менша, а четверта
( )
– в 20 разів менша,
ніж амплітуди
перших двох
гармонік. Цим
пояснюється
факт виділення
частот перших
двох гармонік
функції
)
– в 20 разів менша,
ніж амплітуди
перших двох
гармонік. Цим
пояснюється
факт виділення
частот перших
двох гармонік
функції
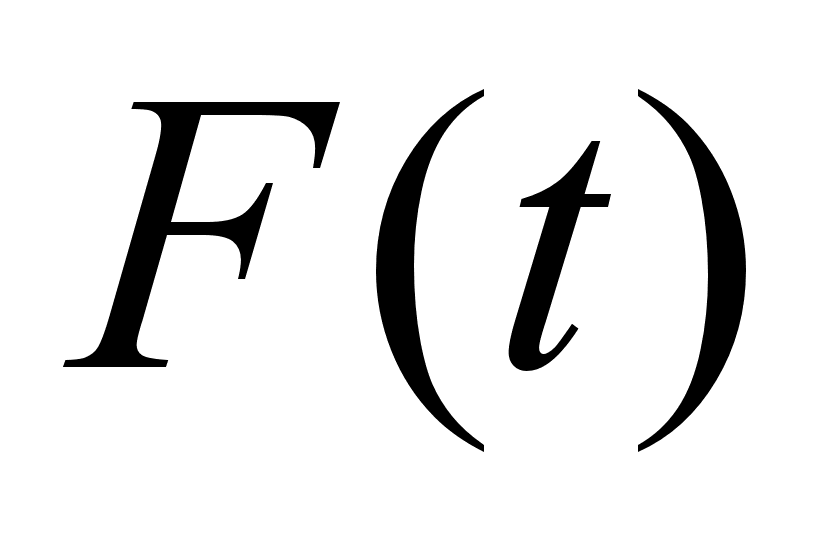 в рішенні
в рішенні
 .
.
Обмежимося
значенням
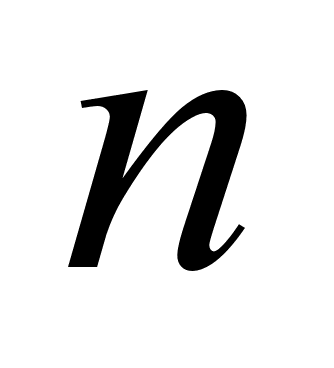 =
3 і побудуємо
рішення
=
3 і побудуємо
рішення
 для випадку
усталених
вимушених
коливань (
для випадку
усталених
вимушених
коливань ( ).
Оскільки
).
Оскільки
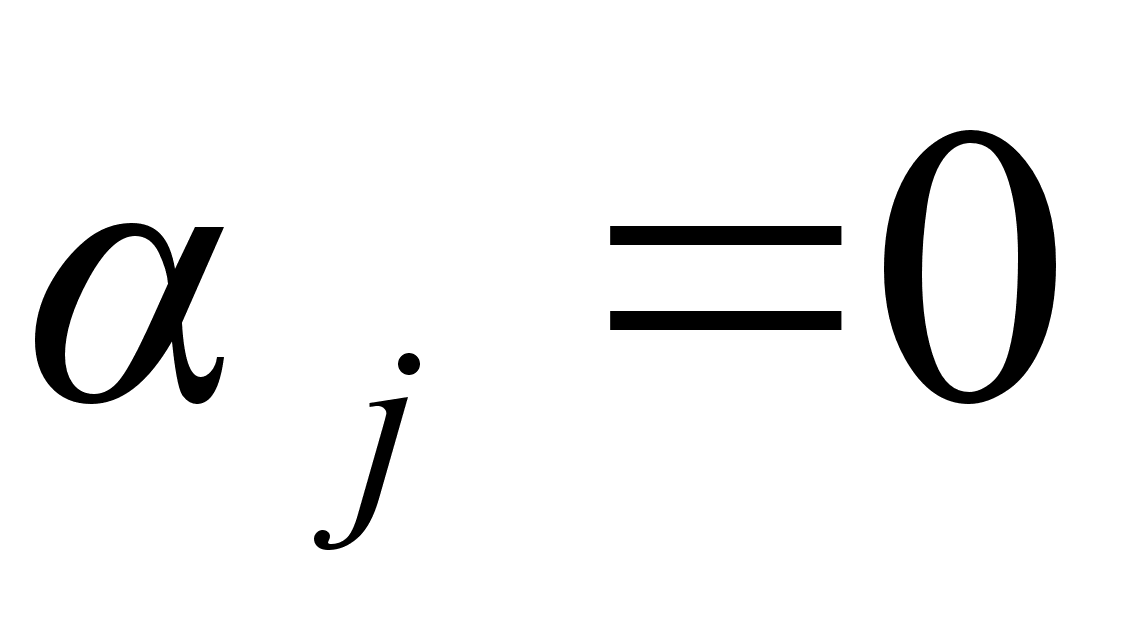 (табл.
1), рішення
(табл.
1), рішення
 має вигляд:
має вигляд:
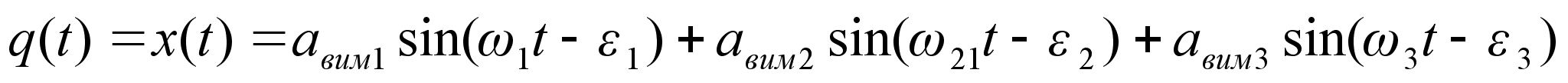 =
=
=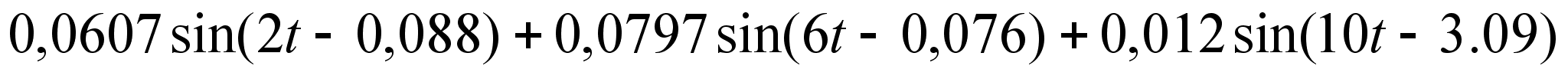 (м).
(м).
Знайдемо
значення узагальненої
координати
 в момент часу
в момент часу
 с:
с:
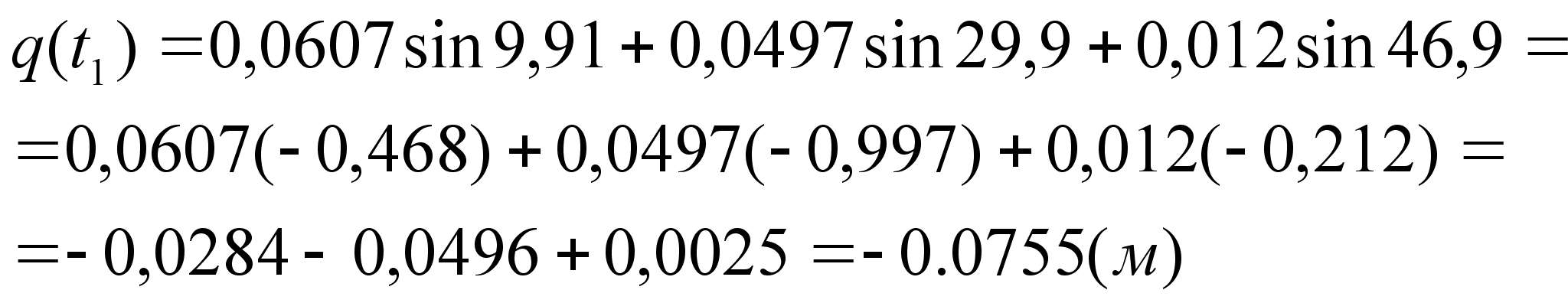
= 4,2%.
Із
розрахунків
випливає, що
визначальними
є значення
рішення для
перших двох
гармонік. При
 =
3 аналітичне
рішення
=
3 аналітичне
рішення
 добре збігається
з “точним”
рішенням на
ЕОМ (відхилення
рішення не
перевищує
= 5%).
добре збігається
з “точним”
рішенням на
ЕОМ (відхилення
рішення не
перевищує
= 5%).
Стисла характеристика програми
 .
.
Если надо – gardemarin@rambler

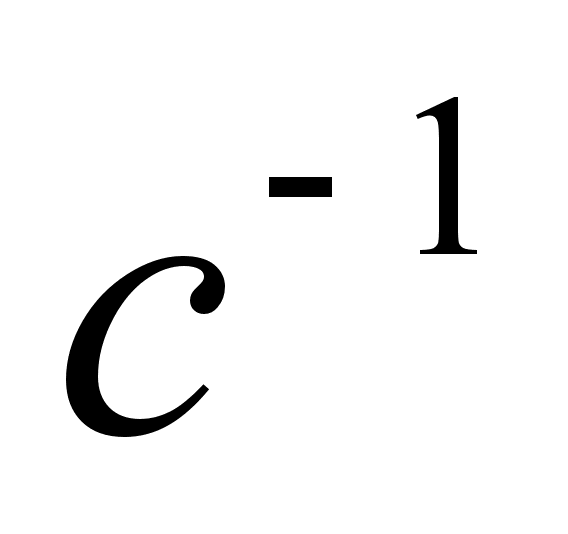
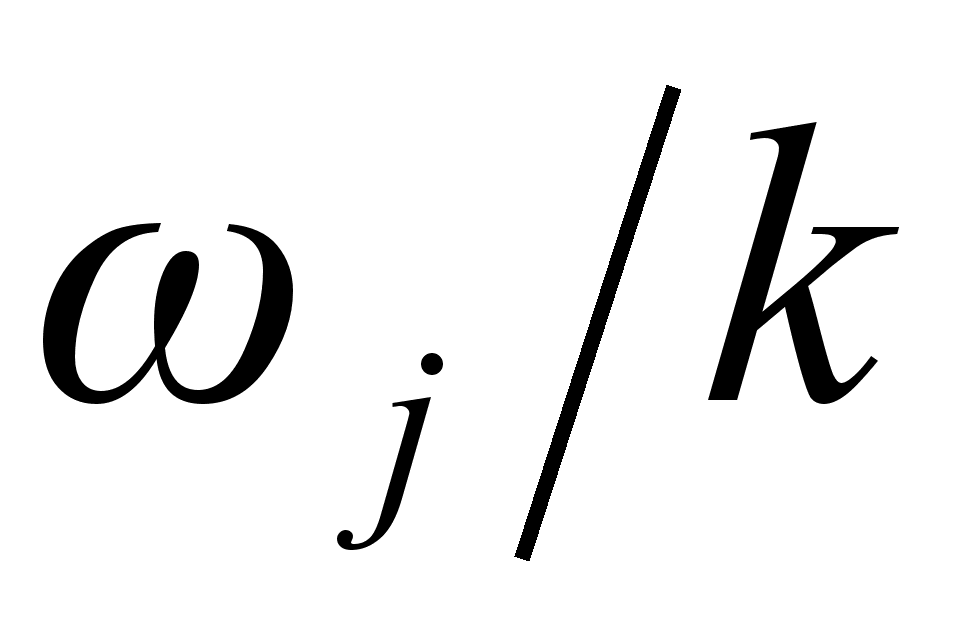
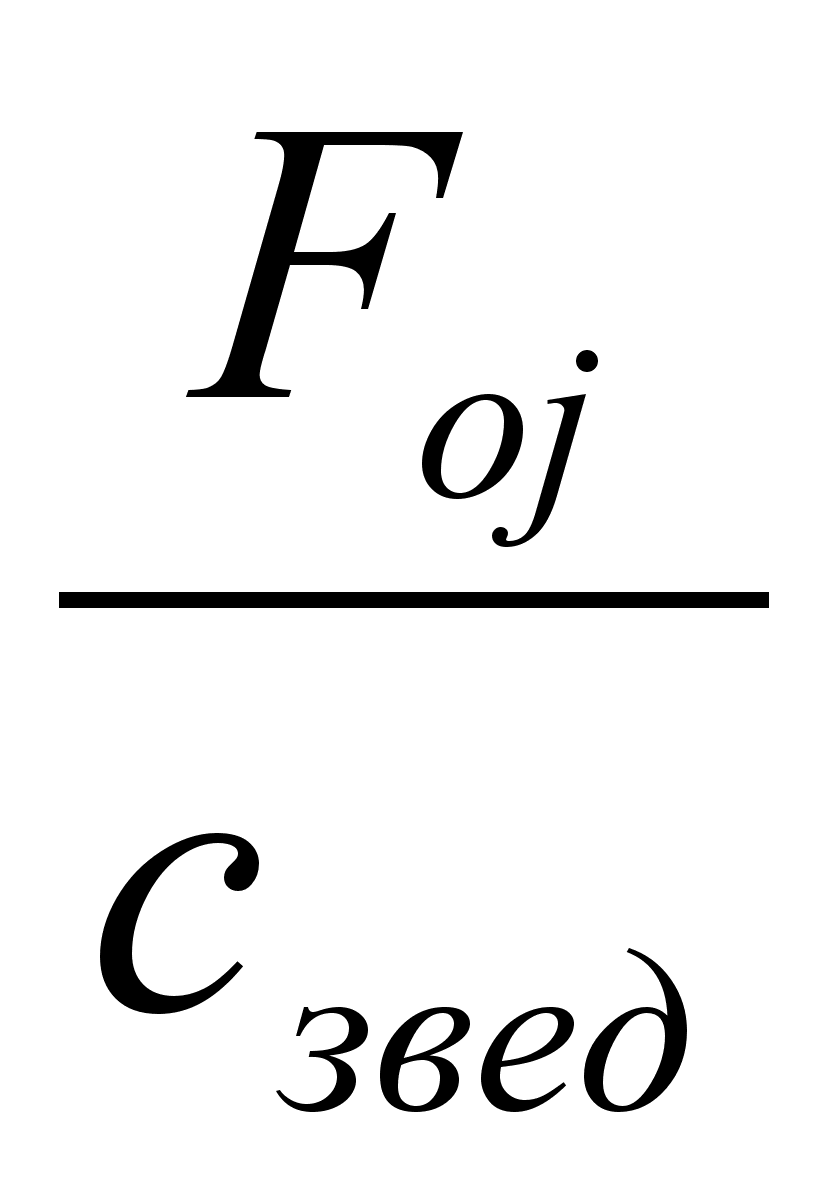 ,
м
,
м