Контрольные задания для заочников по математике

Министерство образования Российской Федерации

государственный технический университет

МАТЕМАТИКА

Методические указания и контрольные задания

для студентов-заочников всех специальностей

Одобрено

редакционно-издательским советом

государственного

технического университета

2004

РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНЫХ РАБОТ

Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса “Математика”, используя учебную литературу. Список рекомендуемой литературы приведен в методических указаниях. Студент может использовать также учебники и учебные пособия, не включенные в данный список, если эти пособия содержат соответствующие разделы учебного курса.

Контрольная работа выполняется в отдельной тетради. На обложке тетради необходимо указать название учебной дисциплины, номер контрольной работы, а также полностью фамилию, имя и отчество студента, его адрес, специальность, номер студенческой группы, шифр (номер зачетной книжки) и дату отправки работы в институт.

Задачи контрольной работы выбираются в соответствии с указаниями преподавателя из таблиц вариантов. Вариант определяется двумя последними цифрами номера зачетной книжки. Предпоследняя цифра номера определяет таблицу вариантов, последняя цифра номера определяет столбец в выбранной таблице. Представленная для рецензирования контрольная работа должна содержать все задачи, указанные преподавателем. Решения задач следует приводить в той последовательности, которая определена в таблице вариантов. Условие каждой задачи должно быть приведено полностью перед ее решением. Контрольная работа должна быть подписана студентом.

Зачет по контрольной работе выставляется по результатам рецензирования и собеседования. Перед собеседованием студент обязан исправить в работе ошибки, отмеченные рецензентом.

Зачет по контрольным работам является обязательным для допуска к сдаче зачетов и экзаменов, которые предусмотрены учебным планом.

ВЕКТОРНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

1. -10. Векторы a, b, c, d заданы координатами в некотором базисе. Показать, что векторы a, b, c образуют базис в пространстве, и найти координаты вектора d в этом базисе.

1. a=(3; 2; 2),b=(2; 3; 1),c=(1; 1; 3),d=(5; 1; 11).

2. a=(1; 2; 3),b=(-2; 3; - 2),c=(3; - 4; - 5),d=(6; 20; 6).

3. a=(4; 2; 5),b=(-3; 5; 6),c=(2; - 3; - 2),d=(9; 4; 18).

4. a=(1; 2; 4),b=(1; - 1; 1),c=(2; 2; 4),d=(-1; - 4; - 2).

5. a=(2; 3; 3),b=(-1; 4; - 2),c=(-1; - 2; 4),d=(4; 11; 11).

6. a=(1; 8; 4),b=(1; 3; 1),c=(-1; - 6; - 3),d=(1; 2; 3).

7. a=(7; 4; 2),b=(-5; 0; 3),c=(0; 11; 4),d=(31; - 43; - 20).

8. a=(3; 2; 1),b=(4; - 1; 5),c=(2; - 3; 1),d=(8; - 4; 0).

9. a=(1; 3; 3),b=(-4; 1; - 5),c=(-2; 1; - 6),d=(-3; 5; - 9).

10. a=(1; 5; 3),b=(2; 1; - 1),c=(4; 2; 1),d=(31; 20; 9).

11. -20. Даны координаты точек A1, A2, A3, A4. Известно, что отрезки A1A2, A1A3, A1A4 являются смежными ребрами параллелепипеда. Требуется найти:

длину ребра A1A2; 2) угол между ребрами A1A2 и A1A3; 3) площадь грани, содержащей вершины A1,A2,A3; 4) объем параллелепипеда; 5) уравнение прямой, проходящей через вершину A1 вдоль диагонали параллелепипеда; 6) уравнение плоскости A1A2A3; 7) угол между ребром A1A4 и гранью, содержащей вершины A1,A2,A3; 8) расстояние от вершины A4 до плоскости A1,A2,A3. Сделать чертеж.

11. A1(0; 3; 2),A2(-1; 3; 6),A3(-2; 4; 2),A4(0; 5; 4).

12. A1(4; 2; 5),A2(0; 7; 2),A3(0; 2; 7),A4(1; 5; 0).

13. A1(-1; 2; 0),A2(-2; 2; 4),A3(-3; 3; 0),A4(-1; 4; 2).

14. A1(4; 4; 10),A2(4; 10; 2),A3(2; 8; 4),A4(9; 6; 4).

15. A1(2; 2; 3),A2(1; 2; 7),A3(0; 3; 3),A4(2; 4; 5).

16. A1(4; 6; 5),A2(6; 9; 4),A3(2; 10; 10), A4(7; 5; 9).

17. A1(0; - 1; 2),A2(-1; - 1; 6),A3(-2; 0; 2),A4(0; 1; 4).

18. A1(3; 5; 4),A2(8; 7; 4),A3(5; 10; 4),A4(4; 7; 8).

19. A1(3; 0; 2),A2(2; 0; 6),A3(1; 1; 2),A4(3; 2; 4).

20. A1(10; 6; 6),A2(-2; 8; 2),A3(6; 8; 9),A4(7; 10; 3).

21. Даны уравнения двух сторон параллелограмма: x+2y+1=0 и 2x+y-3=0. Центр параллелограмма находится в точке A(1; 2). Найти уравнения двух других сторон. Сделать чертеж.

22. Даны две вершины треугольника A(2; 1), B(4; 9) и точка пересечения высот N(3; 4). Найти уравнения сторон треугольника. Сделать чертеж.

23. Даны две противоположные вершины квадрата A(1; 3) и C(-1; 1). Найти координаты двух его других вершин и составить уравнения сторон. Сделать чертеж.

24. Найти уравнения сторон треугольника, если заданы его вершина A(1; 3) и уравнения двух медиан x-2y+1=0, y-1=0. Сделать чертеж.

25. Известны уравнение одной из сторон квадрата x+3y-3=0 и точка пересечения диагоналей N(-2; 0). Найти уравнения остальных ее сторон. Сделать чертеж.

26. Уравнения боковых сторон равнобедренного треугольника 2x-y+8=0, x-2y-12=0. Точка N(4; 0) лежит на основании треугольника. Найти уравнение основания. Сделать чертеж.

27. Найти уравнения сторон треугольника, зная одну его вершину B(2; - 7), а также уравнения высоты 3x+y+11=0 и медианы x+2y+7=0, проведенных из различных вершин. Сделать чертеж.

28. Точка A(5; - 4) является вершиной квадрата, диагональ которого лежит на прямой x-7y-8=0. Написать уравнения сторон и второй диагонали этого квадрата. Сделать чертеж.

29. Уравнение основания равнобедренного треугольника x+y-1=0, уравнение боковой стороны x-2y-2=0. Точка N(-2; 0) лежит на другой боковой стороне. Найти уравнение этой стороны. Сделать чертеж.

30. Даны уравнения медиан треугольника 5x+4y=0 и 3x-y=0 и одна из его вершин A(-5; 2). Найти уравнения сторон треугольника. Сделать чертеж.

31. Составить уравнение и построить окружность, проходящую через точки A(1; 2), B(0; - 1) и C(-3; 0).

32. Составить уравнение и построить линию, расстояние каждой точки которой от точки A(0; 1) в два раза меньше расстояния ее до прямой y-4=0.

33. Составить уравнение и построить линию, сумма квадратов расстояний от каждой точки которой до точек A(-3; 0) и B(3; 0) равна 50.

34. Составить уравнение и построить линию, расстояние от каждой точки которой до точки A(-1; 1) вдвое меньше расстояния до точки B(-4; 4).

35. Составить уравнение и построить линию, сумма расстояний от каждой точки которой до точек A(-2; 0) и B(2; 0) равна 2.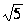

36. Составить уравнение и построить линию, каждая точка которой находится на одинаковом расстоянии от точки F(2; 2) и оси Ox.

37. Составить уравнение и построить линию, расстояния каждой точки которой от точки A(2; 0) и от прямой 5x+8=0 относятся как 5: 4.

38. Составить уравнение и построить линию, расстояния каждой точки которой от начала координат и от точки A(5; 0) относятся как 2: 1.

39. Составить уравнение и построить гиперболу, проходящую через точку N(9; 8), если асимптоты гиперболы имеют уравнения y=±(2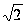/3) x.

40. Составить уравнение и построить гиперболу, вершины и фокусы которой находятся в соответствующих фокусах и вершинах эллипса 5x2+8y2=40.

41. -50. Кривая задана уравнением в прямоугольной системе координат. Требуется: 1) найти уравнение кривой в полярной системе координат, полюс которой совмещен с началом прямоугольной системы координат, а полярная ось – с положительной полуосью Ox; 2) построить кривую по точкам со значениями полярного угла φk=kπ/16.

41. (x2+y2) 2 = 2(x2-y2); 42. (x2+y2) 2 = 4xy;

43. (x2+y2) 2/4 = x2-y2; `44. (x2+y2) 2 = 8xy;

45. (x2+y2) 2 = 6(x2-y2); 46. (x2+y2) 2 = 2(y2-x2);

47. (x2+y2) 2 = - 4xy; 48. (x2+y2) 2 = 4(y2-x2);

49. (x2+y2) 2 = - 8xy; 50. (x2+y2) 2 = 12xy.

ЭЛЕМЕНТЫ АЛГЕБРЫ

51. -60. Решить систему линейных уравнений методом Гаусса.

51.52.

м3x1+ x2+ x3+ x4+ x5= 5, м x1+2x2+ x3+6x4+ x5=4,

н2x1 - x2+3x3 = 4, н3x1 - x2 - x3+ x4+ =1,

о 5x2+6x3+ x4+ =11. о x1+3x2+5x3 =9.

53.54.

м3x1 - x2+ x3+6x4+ x5=6, м5x1+ x2+ x3+3x4+ x5=5,

н x1+ 5x3+ x4-7x5 =6, н - 2x2+4x3+ x4+ x5=3,

о x1+2x2+3x3+ x4+ x5 =6. о x1-3x2+5x3 =2.

55.56.

м - x1+ x2+ x3+2x4+ x5=4, м-2x1 - x2+2x3 =2,

н2x1 + x3 - 3x4+5x5=3, н x1+ x2+4x3+ x4+3x5=8,

о3x1 - x3+6x4+ x5=6. о3x1+ x2 - x3 =5.

57.58.

м2x1+ x3 - x4+ x5=2, м 6x1+ x2+ x3+ 2x4+ x5=9,

н4x1+ x2+ 3x3+ x4+2x5=7, н - x1 - x3+ 7x4+8x5=14,

о - x1+ x3+2x4+ x5=2. о x1+ 2x3+ x4+ x5=3.

59.60.

м-2x1+ 3x3+ x4+ x5=5, м2x1+ 3x3+ x4 =4,

н 3x1+ x2+ x3+6x4+2x5=9, н x1 - x3+2x4+3x5=4,

о - x1+ 2x3 - x4+2x5=3. о3x1+3x2+6x3+3x4+6x5=15.

61. -70. Для данной матрицы A построить обратную матрицу A-1. Правильность построения обратной матрицы проверить, используя матричное умножение.

61. й3 2 1щ 62. й 1 - 5 3щ 63. й4 - 3 2щ

A= к2 3 1 к A= к 2 4 1 к A= к2 5 - 3 к

л2 1 1ы. л-3 3 - 7ы. л5 6 - 2ы.

64. й-2 5 - 6щ 65. й2 - 1 - 1щ 66. й3 - 9 8щ

A= к 1 7 - 5 к A= к3 4 - 2 к A= к2 - 5 5 к

л 4 2 - 1ы. л3 - 2 4ы. л2 - 1 1ы.

67. й1 1 - 1щ 68. й2 3 1щ 69. й7 - 5 0щ

A= к8 3 - 6 к A= к4 - 1 5 к A= к4 0 11к

л4 1 - 3ы. л1 - 2 4ы. л2 3 4ы.

70. й1 7 - 2щ

A= к3 5 1 к

л-2 5 - 5ы.

71. -80. Определить собственные значения и собственные векторы квадратной матрицы второго порядка.

71. й-1 3 щ 72. й4 - 1щ 73. й-6 5щ 74. й-4 - 3 щ

л2 0 ы. л-2 3ы. л 2 - 3ы. л-2 1 ы

75. й-3 2 щ 76. й1 - 2щ 77. й 4 - 1щ 78. й-1 3щ

л 5 - 6ы. л-3 - 4ы. л-2 5ы. л2 - 2ы.

79. й 1 - 2 щ 80. й1 2щ

л-3 6 ы. л3 2ы.

81. -90. Дано комплексное число z. Требуется:

1) записать число z в алгебраической, тригонометрической и показательной формах;

найти все корни уравнения w3+z=0, изобразить эти корни на плоскости комплексной переменной.

_ _ _

81. z=8/(1+iЦ3).82. z=-Ц8/(1+i).83. z=Ц8/(1-i).

_ _ _

84. z=2/(1-iЦ3).85. z=-2/(-i+Ц3).86. z=1/(Ц3+i).

_ _ _

87. z= - 4/(1-iЦ3).88. z=-Ц8/(-i+1).89. z=Ц8/(1+i).

_

90. z=1/(Ц3-i).

ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

91. -100. Построить график функции y = f(x) посредством преобразования графика некоторой простейшей элементарной функции.

91. f(x) = (3x+2) / (2x+3).

92. f(x) = 3cos(2x – 5).

________________

93. f(x) =Ц(4x2+7x –2) / (4x-1).

94. f(x) = 9x2 – 6x + 3.

95. f(x) = ln(x2 – 6x + 9).

96. f(x) = - 2sin(3x + 4).

97. f(x) =2x3 – 18x2 + 54x – 53.

98. f(x) =ln((x+1) - 2 / e2).

99. f(x) =

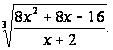
f(x) = (3x2 – 5x + 2) /(2x2 + x – 3).

101. -110. Haйти пределы функций, не пользуясь средствами дифференциального исчисления.

_________ _

101. а) lim (Ц4x2 – x + 3 - 2x); б) lim (Цx – 1) – 1sin(1 – x);

x ® µ x ®1

в) lim (1 + x + x2) 1/x; г) lim (5x - 3x) /(7x – 4x).

x ® 0 x ® 0

102. а) lim (x2+2x–3) /(3x2+14x+15); б) lim x sin((2x + 1) / (x2+4x3));

x® - 3 x ® µ

в) lim (1 – 2sin2x) 1/xsinx; г) lim x – 2 ln(cos2x).

x ® 0 x ® 0

______ _______ _____

103. а) lim (3Ц8x4 + 1 + Цx + 3) / (3Цx + 2(1 + Цx2 + 9));

x ® µ

б) lim sin2(x – 1) / (4x2 + 3x +2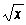); в) lim ;

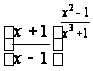x ® µ x®Ґ

г) lim (e2x – 3ex + 2) /x.

x ® 0

__________ ______

104. а) lim (Цx2 + x + 1 - Цx2 - x); б) lim (1 – cos2x) /(x sinx);

x ® µ x ® 0

в) lim((2x2+3x+4) /(2x2+x+1)) –x/2; г) lim [ln(1 + 3lnx) / ln(1 + 4lnx)].

x ® µ x ®1

105. а) lim (3x5 + 2x2 + 1) /(1 + 4x3 – x5); б) lim x – 2sin2(x2 + 2x);

x® µ x ® 0

в) lim 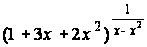; г) lim (esinx – ex) /x.

x ® 0 x ® 0

_______________

106. а) lim (Цx2 + 4x - Цx2 + 6x + 1); б) lim (cos 5x) /(sin 2x);

x ® µ x ® p/2

в) lim ((x2 + 7x + 8) /(x2 + 14x + 1)) – x/3; г) lim (e – ecosx ) /x.

x ® µ x ® 0

_____

107. а) lim (x2 - 5x + 6) /(x3 - 8x + 8); б) lim (1 - Ц1 – x) – 1 sinx;

x ® 2 x ® 0

_____

в) lim (x + Ц1 + x) 3/x; г) lim x – 1 ln(cosx + sinx).

x ® 0 x ® 0

108. а) lim (3x4 – 2x2 + 1) /(2x4 + 3x2 – 2);

x ® µ

б) lim (sinx – sin3x) /(sin6x – sin7x);

x ® 0

в) lim 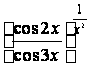; г) lim (ln cosx) /(cos3x – cosx).

x ® 0x ® 0

109. а) lim 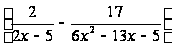; б) lim (cos8x – cos2x) /(cos6x – cos4x);

x®5/2x ® 0

______

в) lim (9 –2x) 1/(4 – x); г) lim ln(x + Цx2 + 1) /x.

x ® 4x ® 0

____________

110. а) lim (x - Цx + 2) /(Ц4x + 1 - 3); б) lim (sin2x– sinx) /(cos4x – cos2x);

x ® 2 x ® 0

в) lim ((2x + 1) /(3x +1)) 1/x; г) lim (ln(3 – 2tgx)) /cos2x.

x®0 x ® p/4

111. -120. Исследовать на непрерывность функцию y = f(x), найти точки разрыва и определить их род. Построить схематический график функции.

111. 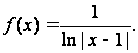112. 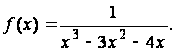113.

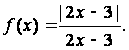
114. 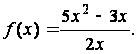115.

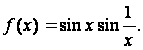
ж (2x2 + 3) /5приxО( - Ґ, 1] ;

116. 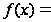н 6 – 5xприx О (1, 3);

и x – 3приx О [3, +Ґ).

117. 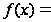arctg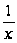.118. 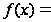x ctgx.

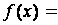
119. 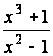.120.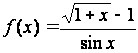

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ И ЭЛЕМЕНТЫ ДИФФЕРЕНЦИАЛЬНОЙ ГЕОМЕТРИИ

121. -130. Найти производную функции одной переменной, исходя из определения производной.

y = tg2x.122. y = ln(3x + 1).123. y = cos(x2).

y = sin(x2 + 2x).125. y = ctg(3x - 2).126. y = Ц 2x2 + 1.

127. y = Ц 2 – cos3x.128. y = Ц 2 + sin2x.129. y = e2x.

y = (x + 1) /(x – 1).

131. -140. Найти производные первого порядка данных функций, используя правила вычисления производных.

1) y = Ц4x4 + tgx; 2) y = x1/2 / sinx;

3) y = ctg5x / x3; 4) y = arctg(ex) + tg(arccos(ex)).

1) y = ln(tg(3x + 2)); 2) y = Ц 1 – x2 arcsinx;

3) y = xtgx; 4) y = (x2 – 1) /(x2 + 1).

1) y = arccos(x2) + arcctg(x2); 2) xy = cos(x – y);

3) y = log2(2x + 1); 4) y = Ц1 – x2 / Ц1 + x2.

1) y = (2 - 5x) / Ц2 – 5x + x2; 2) y = ex – y;

3) y = 2 lnx – x; 4) y = sin2 3t, x = cos4 3t.

1) y = (arcsinx) 1 – x; 2) y = cos2 x + tg2x;

3) x3 + y3 – 3xy = 3; 4) x = t – sin2t, y = 1 – cos 2t.

1) y = sin2x/(1 + sin2x); 2) y = 3arctgx + (arctgx) 3,

3) y = (1 + x2) 1 + 2x; 4) y = tg3t, x = cos2 3t.

1) y = 3 –3x + (3x) –3; 2) y = (x – 1) log5(x2 – 1),

3) y = (x2 + 1) x; 4) y