Теории управления
h
= |1
0|
;
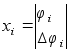 ;
;
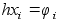
Вектор динамической системы двумерный и динамическая сис-
темы тоже двумерная.
(3)
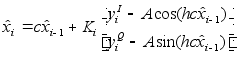
Фильтр
(3) дает оцнеку
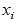 . Реализация
невязки ана-
. Реализация
невязки ана-
логично как в a,b,g - фильтрах.
Синтез аналого-цифрового следящего измерителя.










 Рис.
2 Ф-1 Д АЦП Фильтр
Рис.
2 Ф-1 Д АЦП Фильтр

Калмана

 экстра-
экстра-








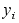 УПЧ
ґ
Ф-3 полятор
УПЧ
ґ
Ф-3 полятор




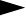

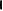
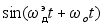 Ф-2 Д
АЦП
Ф-2 Д
АЦП
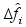

Синтезатор
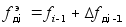

 опоры
опоры
Ф-3 - узкополосный фильтр
Ф-1,Ф-2 - расстроенная пара фильтров

Ф-1 Дискриминационная
 характеристика
:
характеристика
:




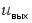 вычитателя
вычитателя





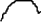
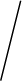 f
f
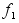
 Ф-2
Df
Ф-2
Df
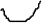
f
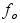

Дискриминационная характеристика - это разность фильтров
Ф-1
и Ф-2. Она формирует
невязку
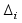 .
.
(1)
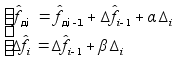
Эта система используется для оценки доплеровской частоты,
меняющейся во времени. Это следует из уравнения (1), где
нижнее уравнение дает поправку доплеровской частоты за
один шаг.Невязка формируется также как в a,b,g - фильтрах.
Глава 7
Устойчивость стохастических систем
В радиоавтоматике все без исключения системы являются
стохастическими, т.е. сама динамическая система описыва-
ется стохастическими разностными уравнениями. Наблюдения
тоже записываются с учетом шумов.
1) Линейные стохастические системы
(1)
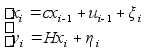 ;
;

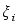 - шум
динамической
системы
- шум
динамической
системы
 - шум
наблюдений
- шум
наблюдений
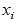 - m-мерный
вектор
- m-мерный
вектор
с - матрица перехода
Устойчивость определяется нормой матрицы ‘c’.
Достаточным условием устойчивости (1) является :
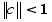 ,
где
,
где
(2)
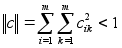 , где
, где
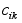 - элементы матрицы
‘c’
- элементы матрицы
‘c’
с =|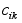 |,
i=1,...,m
; k=1,...,m
|,
i=1,...,m
; k=1,...,m
Если условие (2) выполняется, то система всегда бу-
дет устойчива.
Замечание: В некоторых случаях система может быть устой-
чивой
, если
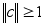 ,
потому что
условие (2) яв-
,
потому что
условие (2) яв-
ляется достаточным, но не необходимым.
Пример стохастической системы 1-го порядка:
(1)’

Оценка
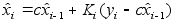 - система будет
устой-
- система будет
устой-
чива
при
0
c>1
мым и достаточным
условием
устойчивости
системы.
Устойчивость
нелинейных
систем
Нелинейная
стохастическая
система : (3)
Устойчивость
нелинейных
динамических
систем опре-
деляется
функцией Ляпунова. Определение
устойчивости
по Ляпунову
для детерминирован- ной
системы.
Вводится
специальная
функция, называемая
функцией Ляпуно- ва.
Обозначается
:
условиям
: 1.
Если x=0,
то
2.
Приращение
функции Ляпунова
во времени
D т.е.
функция должна
быть убывающей:
рают
так:
устойчивости
для системы
(3)
будет
следующим:
1)
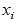 ,
,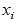 0
0



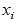

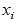

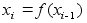
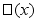 .
Функция удовлетворяет
следующим
.
Функция удовлетворяет
следующим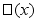 =0
=0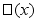
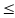 0,
0,



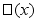 Для
стохастической
системы (3)
Для
стохастической
системы (3)



 обычно
функцию Ляпунова
выби-
обычно
функцию Ляпунова
выби-
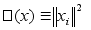 .
А условие
.
А условие
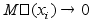 ,
,
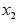 i®Ґ
(ассимптотически)
i®Ґ
(ассимптотически)
