Нильпотентная длина конечных групп с известными добавлениями к максимальным подгруппам
Следствие
2.9. Пусть
 - некоторая
подгруппа
группы
- некоторая
подгруппа
группы
 ,
содержащая
,
содержащая
 ,
тогда
,
тогда
 не обладает
неединичной
нормальной
не обладает
неединичной
нормальной
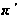 -подгруппой.
-подгруппой.
Действительно,
нормальная
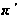 -подгруппа
группы
-подгруппа
группы
 должна содержаться
в центролизаторе
группы
должна содержаться
в центролизаторе
группы
 .
.
Под
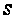 -подгруппой
конечной группы
-подгруппой
конечной группы
 мы подразумеваем
такую подгруппу,
порядок и индекс
которой взаимно
просты. Если
группа
мы подразумеваем
такую подгруппу,
порядок и индекс
которой взаимно
просты. Если
группа
 разрешима и
ее порядок
равен
разрешима и
ее порядок
равен
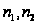 ,
где
,
где
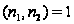 ,
то группа
,
то группа
 обладает
обладает
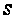 -подгруппами
порядка
-подгруппами
порядка
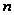 и любые две из
них сопряжены,
а поэтому изоморфны.
и любые две из
них сопряжены,
а поэтому изоморфны.
Теорема
2.10. Если
 - разрешимая
группа порядка
- разрешимая
группа порядка
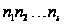 ,
где
,
где
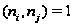 при
при
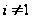 ,
и если подгруппа
группы
,
и если подгруппа
группы
 порядка
порядка
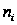 имеет класс
нильпотентности
имеет класс
нильпотентности
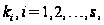 то
то
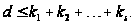
В частности,
для любой конечной
разрешимой
группы
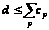 .
.
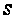 -подгруппа
некоторой
факторгруппы
-подгруппа
некоторой
факторгруппы
 ,
порядок которой
делит
,
порядок которой
делит
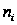 ,
имеет класс
нильпотентности,
не превышающий
,
имеет класс
нильпотентности,
не превышающий
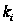 ,
так что мы можем
применить
утверждение
леммы 2.5 и получить
результат
индукцией по
порядку группы
,
так что мы можем
применить
утверждение
леммы 2.5 и получить
результат
индукцией по
порядку группы
 ,
допустив что
,
допустив что
 обладает только
одной минимальной
нормальной
подгруппой.
Это будет
обладает только
одной минимальной
нормальной
подгруппой.
Это будет
 -группа
для некоторого
простого числа
-группа
для некоторого
простого числа
 ,
и мы можем поэтому
предполодить,
что ее порядок
делит
,
и мы можем поэтому
предполодить,
что ее порядок
делит
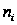 .
Тогда, если мы
возьмем в качестве
.
Тогда, если мы
возьмем в качестве
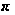 множество
простых долителей
числа
множество
простых долителей
числа
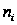 ,
окажется выполненной
предпосылка
леммы 2.5. Если
,
окажется выполненной
предпосылка
леммы 2.5. Если
 - наибольшая
нормальная
- наибольшая
нормальная
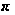 -подгруппа
группы
-подгруппа
группы
 и
и
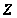 - ее центр, то
по следствию
леммы 2.5
- ее центр, то
по следствию
леммы 2.5
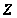 содержит центр
содержит центр
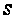 -подгруппы
группы
-подгруппы
группы
 ,
имеющей порядок
,
имеющей порядок
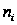 .
Порядок
.
Порядок
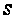 -подгруппы
группы
-подгруппы
группы
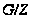 делит
делит
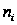 ,
поэтому класс
нильпотентности
ее не более
,
поэтому класс
нильпотентности
ее не более
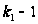 .
Для
.
Для
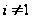
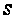 -подгруппы
групп
-подгруппы
групп
 и
и
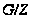 порядка
порядка
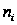 изоморфны, так
что в силу
предположения
индукции, примененной
к
изоморфны, так
что в силу
предположения
индукции, примененной
к
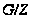 ,
получим
,
получим
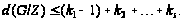
Так
как
 ,
то доказательство
по индукции
проведено.
,
то доказательство
по индукции
проведено.
Прежде
чем применять
лемму 2.5 к доказательству
неравенства
для
 ,
удобно уточнить
её для случая,
при котором
,
удобно уточнить
её для случая,
при котором
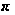 состоит из
одного простого
числа
состоит из
одного простого
числа
 .
Пусть
.
Пусть
 есть
есть
 -разрешимая
группа с верхним
-разрешимая
группа с верхним
 -рядом
(2.2) . Тогда лемма
2.5, применённая
к группе
-рядом
(2.2) . Тогда лемма
2.5, применённая
к группе
 ,
показывает,
что если
,
показывает,
что если
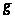 - элемент группы
- элемент группы
 ,
не входящий
в
,
не входящий
в
 ,
то трансформирование
элементом
,
то трансформирование
элементом
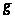 индуцирует
в
индуцирует
в
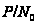 нетождественный
автоморфизм.
Необходимое
уточнение
состоит в замене
группы
нетождественный
автоморфизм.
Необходимое
уточнение
состоит в замене
группы
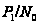 группой
группой
 ,
где
,
где
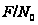 - подгруппа
Фраттини группы
- подгруппа
Фраттини группы
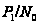 .
Теперь
.
Теперь
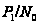 -
-
 -группа,
и таким образом
-группа,
и таким образом
 - элементарная
абелева
- элементарная
абелева
 -группа.
Ясно поэтому,
что автоморфизм
группы
-группа.
Ясно поэтому,
что автоморфизм
группы
 ,
индуцированный
группы
,
индуцированный
группы
 ,
тождественный.
Таким образом,
множество
элементов
группы
,
тождественный.
Таким образом,
множество
элементов
группы
 ,
которое тождественно
трансформирует
,
которое тождественно
трансформирует
 ,
является нормальной
подгруппой
,
является нормальной
подгруппой
 группы
группы
 ,
такой, что
,
такой, что
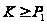 .
По определению
.
По определению
 фактор группа
фактор группа
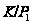 не может быть
не может быть
 -группой,
отличной от
1, так что если
-группой,
отличной от
1, так что если
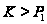 ,
то группа
,
то группа
 должна содержать
элемент
должна содержать
элемент
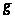 ,
не входящий
в
,
не входящий
в
 и порядка, взаимно
простого
и порядка, взаимно
простого
 .
Тогда
.
Тогда
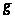 индуцирует
автоморфизм
группы
индуцирует
автоморфизм
группы
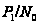 порядка, взаимно
простого с
порядка, взаимно
простого с
 .
Но автоморфизм
.
Но автоморфизм
 -группы,
тождественоой
по модулю подгруппе
Фраттини, имеет
порядок, равный
степени числа
-группы,
тождественоой
по модулю подгруппе
Фраттини, имеет
порядок, равный
степени числа
 .
Таким образом,
.
Таким образом,
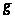 индуцирует
в
индуцирует
в
 нетождественный
автоморфизм,
что противоречит
определению
группы
нетождественный
автоморфизм,
что противоречит
определению
группы
 .
Значит,
.
Значит,
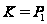 ,
что и требовалось.
Таким образом:
,
что и требовалось.
Таким образом:
Лемма
2.11. Если
 есть
есть
 -разрешимая
группа с верхним
-разрешимая
группа с верхним
 -рядом
(2.2) и если
-рядом
(2.2) и если
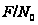 - подгруппа
Фраттини группы
- подгруппа
Фраттини группы
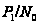 ,
то автоморфизмы
группы
,
то автоморфизмы
группы
 ,
которые индуцированы
трансформированиями
элементами
группы
,
которые индуцированы
трансформированиями
элементами
группы
 ,
представляют
,
представляют

