Волновые равнения
Вывод равнения колебания в электрических проводах.
Электрический ток в проводах характеризуется величиной 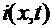 аи напряжением
аи напряжением  акоторые зависят от координат Х точки провода и от времени
акоторые зависят от координат Х точки провода и от времени

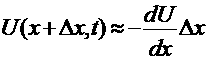
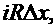 аи индуктивного,
равного
аи индуктивного,
равного 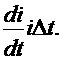 Итак
Итак
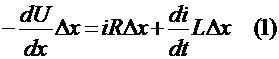
где R и L Цсопротивление и коэффициент индуктивности рассчитанные на единицу длинны провода. Знак минус взят потому, что ток течёт в направлении, обратном возрастанию U.Сокращая на ∆Х,
получим равнение
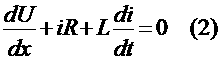
Далее разность токов, выходящего из элемента ∆Х за время ∆t, будет
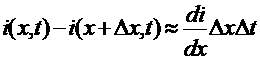
Она расходуется на зарядку элемента, равную 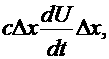 аи на течку через боковую поверхность провода в следствии несовершенства изоляции, равную
аи на течку через боковую поверхность провода в следствии несовершенства изоляции, равную 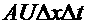
Здесь А- коэффициент течки. Приравняем эти выражения
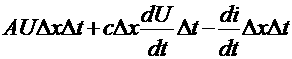
Сократим на 

Уравнения (2) и (3) принято называть телеграфными уравнениями. Составим систему равнений

Из этой системы равнений можно получить равнение,
содержащее только искомую функцию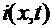

Продифференцируема члены равнения (3) по Х; члены равнения (2) продифференцируем по t и множим их на С.
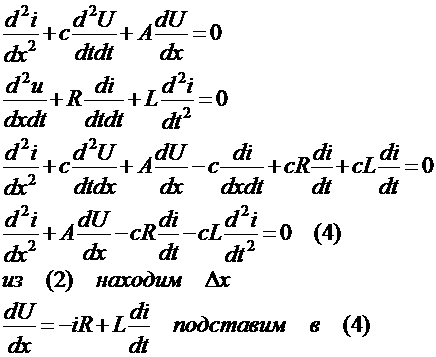

налогичным образом получим равнение для определения 


Если можно пренебречь течкой через изоляцию (А=0) и сопротивлением (R<=0),
то равнения (5) и (6) переходят в волновые равнения:
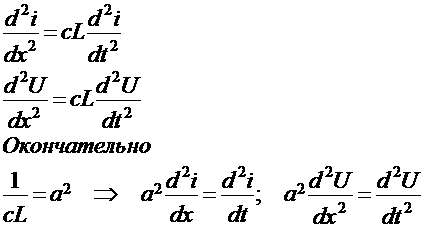
Исходя из физических словий формулируются граничные и начальные словия задачи.
Навоийский Государственный горный институт
Горный факультет
Кафедра Высшей математики
Волновые равнения
Подготовил: студент 2-го курса группы 20-02 ГД
Дерюга А.М.
Навоий 2004 г.

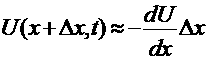
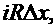 аи индуктивного,
равного
аи индуктивного,
равного 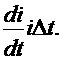 Итак
Итак
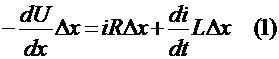
где R и L Цсопротивление и коэффициент индуктивности рассчитанные на единицу длинны провода. Знак минус взят потому, что ток течёт в направлении, обратном возрастанию U.Сокращая на ∆Х, получим равнение
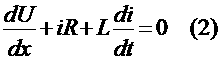
Далее разность токов, выходящего из элемента ∆Х за время ∆t, будет
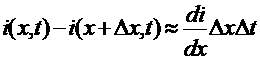
Она расходуется на зарядку элемента, равную 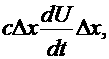 аи на течку через боковую поверхность провода в следствии несовершенства изоляции, равную
аи на течку через боковую поверхность провода в следствии несовершенства изоляции, равную 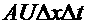
Здесь А- коэффициент течки. Приравняем эти выражения
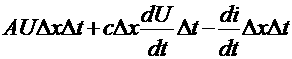
Сократим на 

Уравнения (2) и (3) принято называть телеграфными уравнениями. Составим систему равнений

Из этой системы равнений можно получить равнение,
содержащее только искомую функцию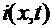

Продифференцируема члены равнения (3) по Х; члены равнения (2) продифференцируем по t и множим их на С.
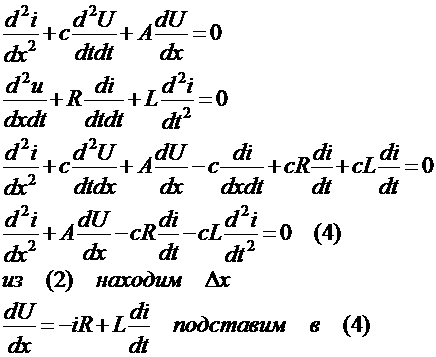

налогичным образом получим равнение для определения 


Если можно пренебречь течкой через изоляцию (А=0) и сопротивлением (R<=0), то равнения (5) и (6) переходят в волновые равнения:
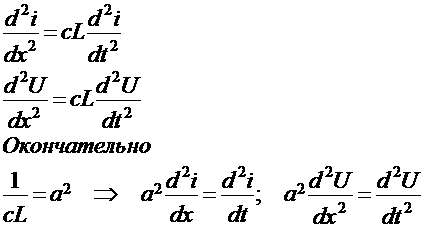
Исходя из физических словий формулируются граничные и начальные словия задачи.
Навоийский Государственный горный институт
Горный факультет
Кафедра Высшей математики
Волновые равнения
Подготовил: студент 2-го курса группы 20-02 ГД
Дерюга А.М.
Навоий 2004 г.

