Основные определения и теоремы к зачету по функциональному анализу
Определение:а Элемент наилучшего приближения - L - линейное многообразие, плотное в E. " Теорема:а Для любого элемента нормированного пространства существует хотя бы один элемент наилучшего приближения из конечномерного подпространства. Теорема:а Для элемента из строго нормированного конечномерного пространства существует единственный элемент наилучшего приближения из конечномерного подпространства. Теорема:а Рисса о существовании почти ортогонального элемента. E-НП LÌE, " Определение:а Полное нормированное пространство- любая фундаментальная последовательность сходиться. Теорема:а О пополнении нормированного пространства.
Любое нормированное пространство можно считать линейным многообразием, плотным в некотором полном нормированном пространстве. Определение:а Гильбертово пространство - нормированное пространство, полное в норме, порожденной скалярным произведением. Теорема:а Для любого элемента гильбертова пространства существует единственный элемент наилучшего приближения в конечномерном подпространстве гильбертова пространства. Определение:а L плотное в E,
если " Теорема:а Чтобы
L было плотно в H ó ортогональное дополнение к L состояло только из нулевого элемента. Определение:а Сепарабельное - нормированное пространство,
содержащее некоторое счетное плотное в нем множество. Определение:а Ортогональное дополнение - множество элементов ортогональных к элементам данного пространства. Определение:а Линейный оператор - отображение, для которого
A(ax+by)=aAx+bAy Определение:а Непрерывный оператор - AxàAx0 при xà x0 Определение: L(X,Y) - пространство линейных операторов Теорема:а Пусть X и Y - полные НП и A - непрерывен на некотором подпространстве пространства X, тогда он непрерывен на всем X. Определение:а Ограниченный оператор - "║x║≤1 <$с:
║Ax║≤c Теорема:а A - ограниченный
ó " Теорема:а Для того чтобы А был непрерывен ó чтобы он была ограничен Теорема: {An} равномерно ограничена è {An}- ограничена. Теорема:а <{Anx} - ограниченно ó {║An║}-
ограничена. Определение:а Сильная (равномерная) сходимость ║An-A║à0, Определение:а Слабая сходимость - " Теорема:а Для того, чтобы имела место сильная сходимость ó {An} сходилась равномерно на замкнутом шаре радиуса 1 Теорема:а Банаха-Штенгауза AnàA nॠслабо è 1) {║An║}- ограничена 2) AnàA, xТÌX, xТ=x Теорема: Хана Банаха. A:D(A)àY, D(A)ÌX è <$ AТ:XàY 1) AТx=Ax, xÎD(A)а 2)
║AТ║=║A║


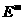
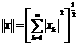 сферическая норма
сферическая норма
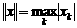 кубическая норма
кубическая норма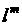
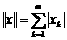 ромбическая норма
ромбическая норма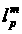
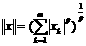
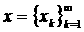
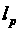
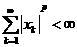
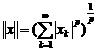
 а или
а или 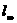 а пространство ограниченных последовательностей
а пространство ограниченных последовательностей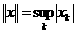
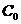 пространство последовательностей, сходящихся к нулю
пространство последовательностей, сходящихся к нулю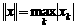
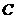 пространство сходящихся последовательностей
пространство сходящихся последовательностей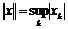
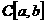 пространство непрерывных на
пространство непрерывных на 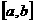 афункций
афункций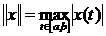
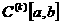 пространство k раз непрерывно дифференцируемых на
пространство k раз непрерывно дифференцируемых на 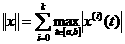
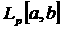 а<- пополнение £p[a,b]
(Гильбертово)
а<- пополнение £p[a,b]
(Гильбертово)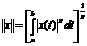
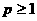
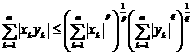
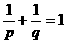 а
а