Расчетные работы по электротехнике
ТипОвая расчетная работ №1.
Дано:
|
R8 |
|
R9 |
|
R1 |
|
R5 |
|
R6 |
|
I1 |
|
I2 |
|
I3 |
|
I11 |
|
I22 |
|
U5 |
|
U6 |
|
Е1 |
|
Ц |
|
+ |
|
Ц |
|
+ |
|
|
|
В |
    |
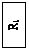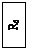Е1=110 В
R1=0,2 Ом
R8=R9=0,4 Ом
R5=R6=1 Ом
U5=60 В
U6=50 В
Найти: токи в ветвях тремя методами.
Решение:
I. Метод законов Кирхгофа.
1) 
а(1);
Запишем I
закон Кирхгофа для зла В: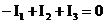
а(2);
2)
для контура I -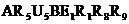 
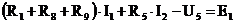а(3);
для контура II -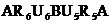 
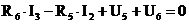а(4);
для контура III - 
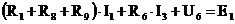а(5).
Решим систему равнений (1), (3), (4):
|
I1 |
-I2 |
-I3 |
0 |
|
(R1+R8+R9)∙I1 |
R5∙I2 |
0 |
E1+U5 |
|
0 |
-R5∙I2 |
R6∙I3 |
-U5-U6 |
Выпишем коэффициенты при неизвестных:
|
1 |
-1 |
-1 |
0 |
|
(R1+R8+R9) |
R5 |
0 |
E1+U5 |
|
0 |
-R5 |
R6 |
-U5-U6 |
Подставим численные значения из исходных данных:
|
1 |
-1 |
-1 |
0 |
|
(0,2<+0,4<+0,4) |
1 |
0 |
110<+60 |
|
0 |
-1 |
1 |
-60<-50 |
Определим Δ, ΔI1, ΔI2, ΔI3 по формулам:
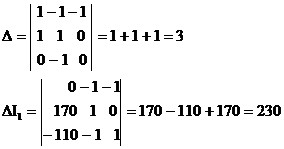
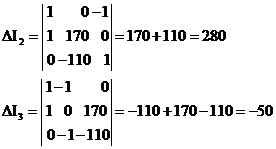
По формулам Крамера определим:
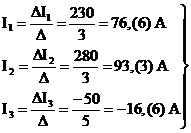а<- токи в трех ветвях.
3)
76,(6)-93,(3)+16,(6)=0
II. Метод контурных токов.
Пусть в каждом контуре протекает только один контурный ток. В первом ток I11, во втором ток I22.
Запишем II закон Кирхгофа для первого контура:
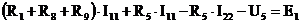
Запишем II закон Кирхгофа для второго контура:
Решим систему этих равнений и определим контурные токи:
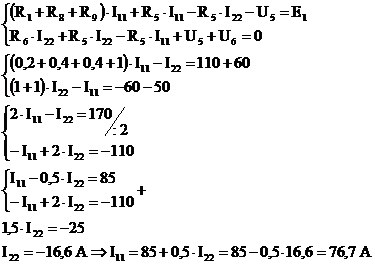
Токи во внешних ветвях равны контурным токам, значит:
I1=I11=76,7 A - тока в первой ветви.
I3=I22=-16,6 - тока в третей ветви.
В смежной ветви ток равен разности контурных токов:
I2=I22-I22=76,7+16,6=93,3 A - ток во второй ветви.
. Метод зловых напряжений.
К злам А и В подводится напряжение UAB - зловое, направление которого выбирается произвольно.
SHAPEа * MERGEFORMAT
|
I3 |
|
R8 |
|
R9 |
|
R1 |
|
R5 |
|
R6 |
|
I1 |
|
I2 |
|
U5 |
|
U6 |
|
Е1 |
|
Ц |
|
+ |
|
Ц |
|
+ |
|
|
|
В |
|
UAB |
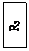
1)
I закон Кирхгофа для зла А: а(1);
2)
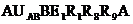
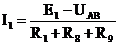а(2);
II закон Кирхгофа для контура II
-
а(3);
II закон Кирхгофа для контура III
- 
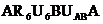
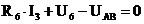
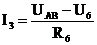а(4);
Для определения напряжения между злами UAB уравнения (2), (3), (4) необходимо подставить в равнение (1):
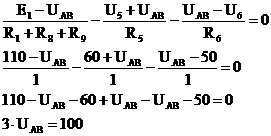
а<- напряжение между узлами А и В.
Токи в ветвях определим по равнениям (2), (3), (4):
а<- токи в трех ветвях.
ТипОвая расчетная работ №2.
|
I |
|
Z |
|
U |
 |
Дано:
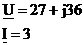
Найти:
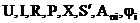
Решение:
1)
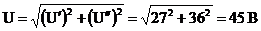а<- действующее значение напряжения.
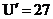а<- действительная часть
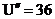а<- мнимая часть
2)
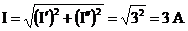а<- действующее значение тока.
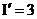а<- действительная часть
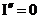а<- мнимая часть
3) R (активное сопротивление) по закону Ома.
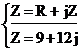а<- полное сопротивление.
R=9 Ом
4)
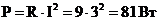а<- активная мощность.
5)
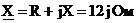а<- реактивное сопротивление.
6)
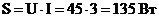а<- полная мощность.
7)
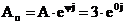а<- показательная форма записи.
Ψ=0
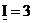
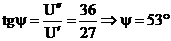
а<- показательная форма записи.
8) Ψi=53
|
+j |
|
- |
|
-1 |
|
+1 |
|
3 |
|
I |
|
Ψ<=53 |
|
U |
|
27 |
|
36 |
 |
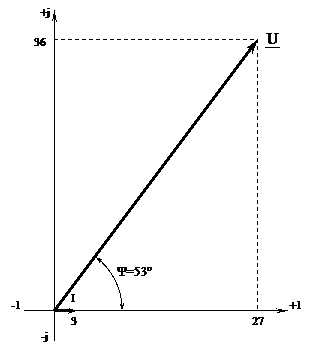ТипОвая расчетная работ №4.
Дано:
Za<=Zb<=Zc<=1,5+ Uп=220 В Определить: Iл - линейный ток Iф - фазный ток Р - активная мощность Q - реактивная мощность S - полная мощность Построить: Векторную диаграмму токов и напряжения. Решение: 1)
На схеме UA, UB, UC - фазные напряжения; UAB, UBC, UCA - линейные напряжения; ZA, ZB, ZC Цфазные сопротивления нагрузок; 2)
Определение фазного сопротивления нагрузок: Схема будет симметричной если UA<=UB<=UC<=UФ=127 В 3)
Определение комплексов напряжений в фазах А, В, С: 4)
Определение фазных токов: 5)
Действующие значения фазных токов: 6) При соединении фаз источника энергии и приемника звездой линейные токи равны соответственно фазным токам. В случае симметричного приемника действующие значения всех линейных и фазных токов одинаковы, т.е. Iп= Iф IА= IВ= IС=
IП=50,8 А 7)
Определение мощности в фазах: где Действующее значение полной мощности Т.к. S<=
8) +1 -1 30,48 19,95 -40,64 -6,07 -50,43 -63,5 -109,98 109,98 +j - 127 UA UB UC IB IA IC 46,72
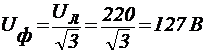
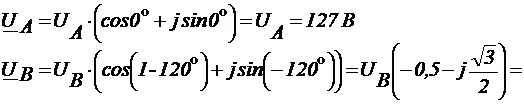
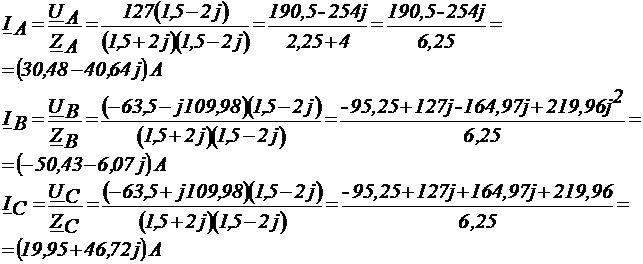
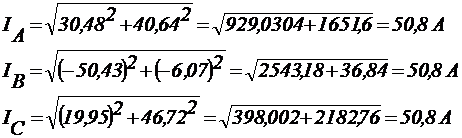
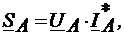
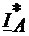а<-
комплексно-сопряженное число.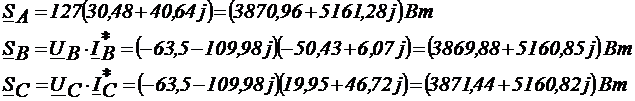
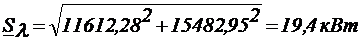
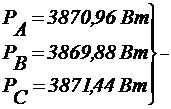активная мощность.
реактивная мощность.
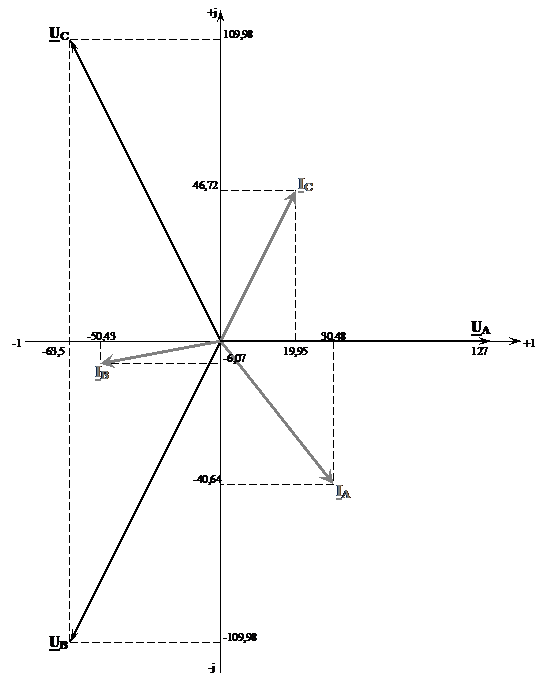Диаграмма:
Типавая расчетная работ №5.
Дано:
|
a |
|
в |
|
с |
|
n |
|
Zca |
|
Zbc |
|
Zab |
|
a |
|
в |
|
Ica |
|
Ibc |
|
Iab |
|
Ia |
|
Ic |
|
Ib |
Za<=Zb<=Zc<=1,5+Uл=220 В
Определить:
Iл - линейный ток
Iф - фазный ток
Р - активная мощность
Q - реактивная мощность
S - полная мощность
Построить:
Векторную диаграмму токов и напряжения.
Решение:
9) Uл=Uф=220 В
UAB=UBC<=UCA<=220 В
Записать комплексы фазных напряжений
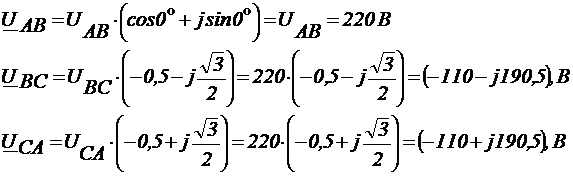
10) Определение комплексов токов в фазах: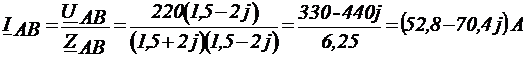 
11) Действующие значения фазных токов:
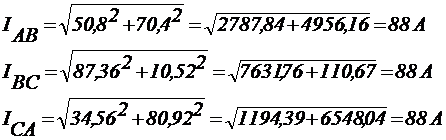
12) При соединении "треугольник" в трехфазной симметричной системе справедливы соотношения: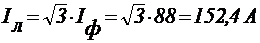 
13) Определение мощности в фазах:
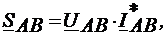
где 
а<-
комплексно-сопряженное число.
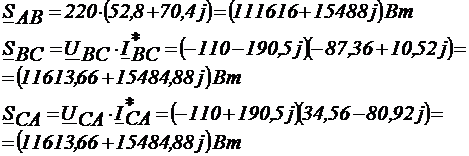
Тогда полная мощность всей цепи определяется:
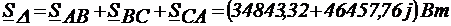
Действующее значение полной мощности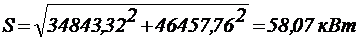 
Т.к. S<=
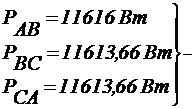активная мощность.
реактивная мощность.
14)
|
+1 |
|
-1 |
|
30,48 |
|
19,95 |
|
-40,64 |
|
-6,07 |
|
-50,43 |
|
-63,5 |
|
-109,98 |
|
109,98 |
|
+j |
|
- |
|
127 |
|
UA |
|
UB |
|
UC |
|
IB |
|
IA |
|
IC |
|
46,72 |
Диаграмма: