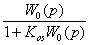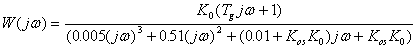Применение метода частотных диаграмм к исследованиям стойчивости систем с логическими алгоритмами правления
Московский Государственный Технический ниверситет им. Н.Э. Бауман
Курсовая работ по курсу Нелинейные САУФ
на
тему:
Применение метода частотных круговых диаграмм к исследованию стойчивости систем с логическими алгоритмами правления.
Выполнил: ст-т гр. АК4-81
Смык В.Л.
Руководитель: профессор
Хабаров В.С.
Реутов 1997 г.
Применение метода частотных круговых диаграмм к исследованию стойчивости систем с логическими алгоритмами правления.
На ранней стадии развития теории автоматического регулирования требование стойчивости работы системы было первым и обычно единственным и содержание большинства теоретических исследований сводилось к иследованию устойчивости.
Термин устойчивость настолько выразителен, что он сам за себя говорит,-отмечают в начале изложения теории стойчивости Ж. Ла Салль и С. Лефшец [1]. Это вполне справедливо, но, несмотря на это, неточности и нелогичности можно встретить как раз не в математических, в смысловых понятиях и терминах.
Устойчивостью любого явления в обиходе называю его способность достаточно длительно и с достаточной точностью сохронять те формы своего существования, при трате которых явление перестает быть самим сабой. Однако не только в обиходе, но и в научной терминалогии устойчивым называют не явление, систему, в корой оно наблюдается, хотя это не оправдывает логически. стойчивы ли физические тела - шар или куб? Такой вопрос будет иметь смысл, если речь идет о материале, из которого они сделаны. (Металлический шар
устойчив, шар из дыма нет.) Теорию управления интересует, однако, не эта прочнасная стойчивость. Подразумевается, что система правления как инженерная конструкция заведома стойчива, и в теории изучается стойчивость не самой системы, ее состояний и функционирования. В одной и той же системе одни состояния или движения могут быть стойчивыми, другие не стойчивыми. Более того, одно и то же жвижение может быть стойчивым относительно одной переменной и неустойцивым относительно другой - это отмечал еще А.М. Ляпунов [2]. Вращение ротора турбины стойчиво по отношению к гловой скорости и неустойчиво относительно гла поворот вала. Движение ракеты стойчиво относительно траектории и неустойчиво по отношению к неподвижной системе координат. Поэтому нужно оговаривать, стойчивость какого состояния или движения в системе и относительно каких переменных изучается. Так же есть много методов для оценки самой стойчивости. Мы рассмотрим как можно оценить стойчивость системы с логическим алгоритмом правления методом круговых диаграмм.
Рассмотрим теоретическую часть и посмотрим что из себя представляет круговой критерий. Пусть дана система
.
где система (1), дополненая соотношением
Для абсолютной экпоненциальной стойчивости системы (1) в классе М(
а достаточно, чтобы при всех Re{[1+ Круговой критерий вытекает из квадратичного критерия для формы F( F(j Из этой формулы после сокращения на |
В (3)
Круговой критерий представляет собой распространение линейных частотных критериев стойчивости Найквиста, Михайлова и других на линейные системы с одним линейным или нелинейным, стационарным или нестационарным блоком. Он получается из (3), если вместо передаточной матрицы использовать частотную характеристику линейной части W(j
Обозначая комплексную переменную W(j Re[(1+ Re[(1+ Re[z(1+ Пусть С(
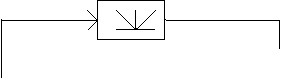
Круговой критерий обеспечивает также абсолютную стойчивость для системы с любым блоком, вход ( Рисунок 1, а. Рассмотрим систему,
приведенную на рис. 2.
Рисунок 2.
Здесь W
W Алгоритм регулятора имеет вид: g=( В форме равнений Коши рассматриваемая система имеет вид: где
<- k
Соответствие записей системы на рис. 2 достигается, когда при W при W(p)= Причем для обоих случаев (11) и (12)
имеет место соотношение В соответствии с изложенным одинаково справедливо рассматривать в виде структурной схемы на рис. 2 с известным линейными операторами -
Дополнительно отметим, что структурная интерпритация рассматриваемой системы на рис. 2 имеет еще одну структурную схему описания, приведенную на рис. 3.
Рисунок 3. Это означает, что аналитической записи
(10) соответствуют два структурных представления исследуемой СПС, причем второе позволяет рассматривать систему (10) как релейную систему с изменяемым ограничение, когда Далее перейдем к анализу нашего метода. Согласно частотной теоремы (10), для абсолютной стойчивости системы на рис. 3 лостаточно, чтобы при всех Re{[1+ гадограф Для исследуемой системы словие (3) добнее записать в виде (4) и (5).
На рис. 4 приведенны возможные нелинейные характеристики из класса М(
у б
в г Рисунок 4. В рассматриваемом случае (10) при W W(p)= W
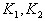
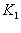 £
£
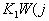
 ¹<-¥ ,
¹<-¥ ,
 ¹<+¥. Случай, когда либо
¹<+¥. Случай, когда либо  а<=<-¥, либо
а<=<-¥, либо  а<=<+¥ рассматривается аналогично.
а<=<+¥ рассматривается аналогично.
 £0, если
£0, если  ¹<-¥ ,
¹<-¥ ,
 ¹<+¥.
(4)
¹<+¥.
(4)
 ¹<-¥ ,
¹<-¥ ,
 ¹<+¥. (5)
¹<+¥. (5)
 £0, если
£0, если  ¹<-¥ ,
¹<-¥ ,
 ¹<+¥. (6)
¹<+¥. (6)
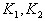
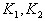

 ас центром на оси абсцисс, причем область С будет внутренностью этой окружности, если
ас центром на оси абсцисс, причем область С будет внутренностью этой окружности, если 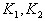
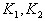

 0, то область С будет полуплоскостью, ее граница -
вертикальной прямой, проходящей соответственно через -1/
0, то область С будет полуплоскостью, ее граница -
вертикальной прямой, проходящей соответственно через -1/ аили -1/
аили -1/ На рисунке 1 показаны границы в плоскости z для различного расположения секторов (
На рисунке 1 показаны границы в плоскости z для различного расположения секторов (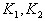









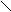

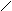
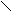





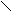

 Х
Y
Х
Y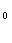 у
у 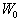 Z
Z (-)
(-) 
 G(p)
G(p)

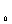
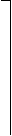
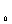

 (8)
(8) W(p)=
W(p)=






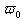 апри gx>0
апри gx>0  Y
Y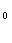 (9)
(9) <-
<-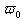 апри gx<0,
апри gx<0,


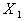





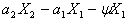 (10)
(10)



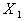
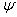
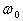 апри g
апри g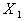

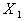

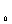
 ав равнениях (10)
имеем:
ав равнениях (10)
имеем: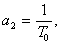 а
а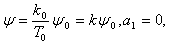 (11)
(11)
 имеем:
имеем: (12)
(12)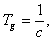 (13)
(13) 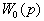 аи G(p) или в виде формы Коши (10).
аи G(p) или в виде формы Коши (10).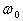










 а
а











 а(-)
а(-)

 асоответствовал критерию Найквиста.
асоответствовал критерию Найквиста. W(j
W(j




 а
а


 >
>
 0а
0а

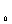

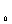
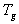




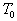
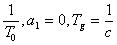
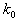









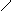











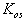

 а<- варьируемая величина,
а<- варьируемая величина,