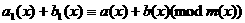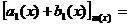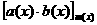Многочлены над кольцом классов вычетов
1. Определение многочлена. 3
2. Операции над многочленами. 4
3. Кольцо многочленов над область целостности. 8
4. Схема Горнера и теорема Безу. 10
5. Делимость многочленов. 13
6. Вычисление наибольшего общего делителя. 15
7. Наименьшее общее кратное. 18
8. Сравнения многочленов по многочлену. 19
9. Классы вычетов. 20
1. Определение многочлена.
В школьной алгебре одночленом от некоторой буквы 
Буква Два полинома называются формально равными, если они, в канонической записи, составлены из одинаковых одночленов. Ясно, что формально равные полиномы равны тождественно, т.е.
принимают одинаковые значения при каждом значении буквы Наша задача сейчас состоит в том, чтобы несколько расширить понятие полинома. Пусть K - некоторое коммутативное ассоциативное кольцо с единицей, и пусть 2.
Операции над многочленами. Два полинома считаются равными, если они составлены в канонической записи из одинаковых одночленов, т.е. Суммой двух полиномов называется полином, получающийся посредством объединения одночленов, составляющих слагаемые. Разумеется, после объединения следует привести подобные члены. Таким образом, легко видеть, что операция суммирования (сложения) многочленов обладает такими же свойствами, что и операция сложения элементов кольца K, т.е. ассоциативна, коммутативна;
полином, все коэффициенты которого нули, является нейтральным элементом сложения полиномов; для каждого полинома существует ему противоположный, противоположный к полиному Произведением двух полиномов называется полином, составленный из произведений всех членов первого сомножителя на все члены второго. Здесь снова возможно приведение подобных членов. Таким образом, Умножение многочленов ассоциативно. Это доказывается следующим образом: если помимо многочленов Умножение многочленов дистрибутивно относительно сложения, это вытекает из равенства Нетрудно видеть, что многочлен В данном выше определении одночлена и полинома имеется одно сомнительное место. Именно, было сказано, что
1.
2.
3.
Легко проверяется коммутативность и ассоциативность сложения и множения и дистрибутивность умножения со сложением. Далее ясно, что 4. Рассмотрим теперь последовательность (0, 1, 0,..., 0,...), обозначив ее буквой Итак,
при определении многочлена существенны лишь коэффициенты Пусть При сложении многочленов 3. Кольцо многочленов над областью целостности. Далее будем рассматривать только многочлены с коэффициентами из области целостности K (кольцо без делителей нуля называют областью целостности), т.е. из кольца K, в котором произведение двух элементов может равняться нулю, если только один из сомножителей равен нулю. Это всегда будет подразумеваться, даже если не будет оговорено специально. При произведении многочленов Эта формула является точнением неравенства (5) для случая, когда в кольце K нет делителей нуля. Формула (6) также справедлива и тогда, когда один из многочленов Теорема
1. Кольцо многочленов над областью целостности само является областью целостности. Данное нами алгебраическое определение многочлена не содержит никакого поминания о функциях. Тем не менее, с каждым многочленом над областью целостности K можно естественным образом связать функцию, которая определена на K и принимает значения в K. Пусть где выражение в правой части понимается как результат операций в кольце K. Получаемый при этом элемент Покажем,
что сложение и множение многочленов согласуются с обычными операциями,
производимыми над функциями, когда складываются или, соответственно,
перемножаются значения функций в каждой точке. Рассмотрим два многочлена: Пусть теперь Таким образом, функция, определяемая суммой
(соответственно произведением) двух многочленов, есть сумма (соответственно произведение) функций, определяемых этими многочленами. Вообще говоря, соответствие между многочленами и определяемыми ими функциями не является взаимно однозначным. Однако, если кольцо K бесконечно,
то различным многочленам из кольца K[ В кольце многочленов деление в обычном смысле слова, как правило, невозможно. Например, в кольце Если для полиномов Прежде всего становим,
что всегда осуществимо так называемое деление с остатком: Теорема 2. Пусть Доказательство. Естественно искать откуда последовательно определяют коэффициенты Равенство Теорема доказана. Кроме того, получен очень добный способ вычисления коэффициентов a0 a1 a2 ... an-1 an c b0 b1 b2 ... bn-1 c Элементы нижней строки вычисляются последовательно по формулам (8): Элемент Следствие (теорема Безу). Многочлен Доказательство. Пусть Пусть Теорема 3. Число корней ненулевого многочлена не превосходит его степени. Доказательство. Докажем это тверждение с помощью индукции по степени многочлена. Многочлен нулевой степени вообще не имеет корней, так что для него тверждение теоремы справедливо. Предположим теперь,
что тверждение теоремы справедливо для всех многочленов степени Следствие. Многочлен степени не выше Иначе говоря, существует не более одного многочлена степени не выше Доказательство. Предположим, что Теорема 4. Если кольцо K бесконечно, то равенство функций, определяемых двумя многочленами из кольца K[ Доказательство. Пусть многочлены Для конечного кольца K тверждение теоремы 4 неверно. Однако при некоторых дополнительных предположениях и в этом случае оказывается возможным из равенства функций, определяемых двумя многочленами, сделать вывод о равенстве самих многочленов. Теорема 5 (алгоритм Евклида). Пусть K - коммутативное кольцо, Доказательство. Пусть Если Предположим, что теорема доказана для многочленов степени Что касается единственности, то предположим, что В словии теоремы требуется обратимость элемента Следствие. Пусть
K - коммутативное кольцо, Пример. Многочлен
24 <-36 <-70
97 Итак, Наибольший общий делитель двух многочленов причем Пример. В кольце
Для добства множим полученный остаток на
Полученный остаток разделим на 9 и выполним третье деление:
0 Поскольку остаток равен нулю, то Наибольший общий делитель нескольких многочленов Для того чтобы найти наибольший общий делитель многочленов Докажем формулу (10).
Согласно определению наибольшего общего делителя, делители многочлена Наибольший общий делитель
d двух многочленов Для нахождения линейного выражения наибольшего общего делителя d можно воспользоваться алгоритмом Евклида. В самом деле, первое из равенств (9) дает следующее линейное выражение многочлена r1 через Пример. Найдем линейное выражение наибольшего общего делителя d многочленов Результаты делений с остатком, выполненных при решении предыдущего примера, показывают, что Линейное выражение любого многочлена На практике линейное выражение многочлена Наименьшим общим кратным многочленов Теорема Для двух многочленов Доказательство. Для доказательства формулы (23)
положим Многочлен Из формулы (12) вытекает Следствие. Наименьшее общее кратное двух взаимно простых многочленов равно их произведению. 8.
Сравнения многочленов по многочлену. Пусть, например, будем называть эквивалентными, если они определяют одну и ту же функцию на
Теорема 6. Если многочлены Определение. Два многочлена Пример. Многочлены Теорема 7. Для любых многочленов Доказательство. Разделим многочлены Если Теорема 8. Для многочленов Где Доказательство. Из словия, согласно теореме 7,
имеем Складывая, вычитая и перемножая последние равенства, получим: Отсюда видно, что разность Теорема 9. Если т.е. обе части сравнения и многочлен можно делить и множать на один и тот же многочлен. Доказательство. Так как И теперь эта теорема следует непосредственно из теоремы 7. 9.
Классы вычетов. Определение. Класс всех многочленов, сравнимых с многочленом Определим на множестве Определение. Для любых Таким образом, чтобы сложить
(перемножить) классы Докажем, что определение корректно. Действительно, пусть, т. е. Следовательно, результаты операций над классами не зависят от выбора представителей, т. е. операции определены корректно.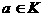
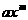 арассматривается как формальная запись. Для одночленов естественным образом определяются действие приведения подобных членов
арассматривается как формальная запись. Для одночленов естественным образом определяются действие приведения подобных членов 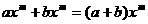 аи действия множения
аи действия множения 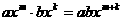 многочленом или полиномом от
многочленом или полиномом от 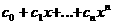
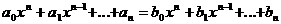 ав том и только в том случае, если
ав том и только в том случае, если 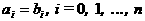
 а
а а
а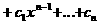
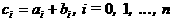
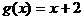
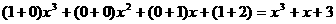
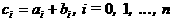 (1)
(1) аявляется полином
аявляется полином 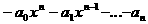
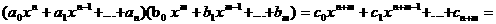 а
а
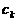 апри
апри 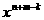 аравен
аравен 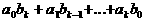
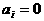 апри
апри 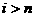 аи
аи 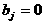 апри
апри 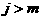
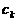 апрост: приводятся такие подобные слагаемые при произведении одночленов
апрост: приводятся такие подобные слагаемые при произведении одночленов 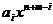 аи
аи 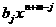
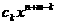 а т.е.
а т.е. 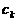
 аи
аи 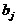 апри
апри 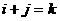
 (2)
(2)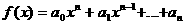 аи
аи 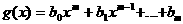 адан еще многочлен
адан еще многочлен 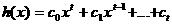

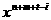
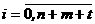 ав произведении
ав произведении 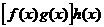 абудет служить элемент
абудет служить элемент 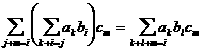
 а<- равное ему число
а<- равное ему число 

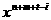 ав многочлене
ав многочлене 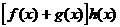
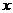 ав многочлене
ав многочлене 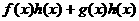
 а(где 1 - единица кольца K) играет роль единицы при множении многочленов. Таким образом, множество полиномов от буквы
а(где 1 - единица кольца K) играет роль единицы при множении многочленов. Таким образом, множество полиномов от буквы 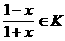 аи т.д. Однако мы можем избавиться от "сомнительной" буквы
аи т.д. Однако мы можем избавиться от "сомнительной" буквы 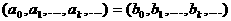 атогда и только тогда,
когда
атогда и только тогда,
когда 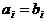
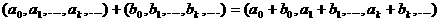

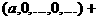 а
а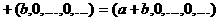 аи
аи 

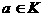 аотождествляется с последовательностью
аотождествляется с последовательностью 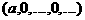
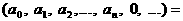 а
а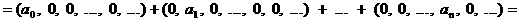 а
а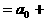
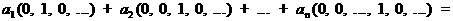 а
а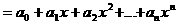 K[
K[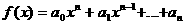 (3)
(3)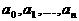
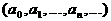
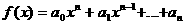
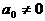
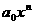 аназывается высшим (старшим) членом полинома
аназывается высшим (старшим) членом полинома 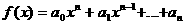 аи
аи 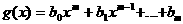 апо формуле (1) мы видим, что формула для суммы не содержит членов, степень которых выше, чем
апо формуле (1) мы видим, что формула для суммы не содержит членов, степень которых выше, чем 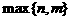
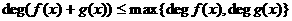 (4)
(4)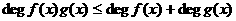 (5)
(5)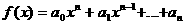 степени
степени 
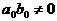 аи, значит,
аи, значит, 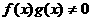
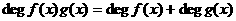 (6)
(6)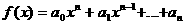 а<- многочлен с коэффициентами из K. Для любого
а<- многочлен с коэффициентами из K. Для любого 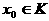 аположим
аположим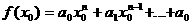 , (7)
, (7) аназывается значением многочлена
аназывается значением многочлена 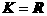
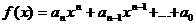

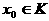
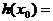
 а<=
а<= 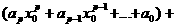 а
а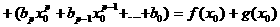
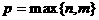
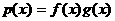 а<- произведение многочленов
а<- произведение многочленов 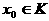
 а
а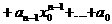
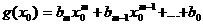 K (в частности, коммутативностью и ассоциативностью умножения), получим:
K (в частности, коммутативностью и ассоциативностью умножения), получим: 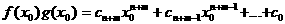

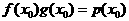
4. Схема Горнера и теорема Безу.
 амногочлен
амногочлен 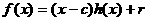 апри
апри 
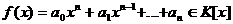 аи
аи 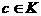 Найдутся полином
Найдутся полином  аи элемент
аи элемент  атакие, что
атакие, что 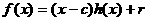 При этом
При этом 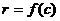
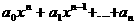 а<= =
а<= = ас коэффициентами многочлена, полученного после раскрытия скобок и приведения подобных, в правой части этого равенства приводит к цепочке равенств
ас коэффициентами многочлена, полученного после раскрытия скобок и приведения подобных, в правой части этого равенства приводит к цепочке равенств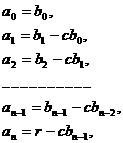
 (8)
(8)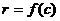 анепосредственно следует из равенства
анепосредственно следует из равенства 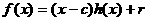 апосле подстановки в последнее вместо
апосле подстановки в последнее вместо
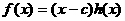
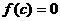
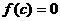
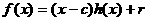 абудет
абудет 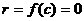
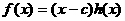


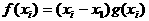
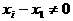 K не имеет делителей нуля, то
K не имеет делителей нуля, то 


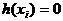 апри
апри 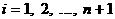
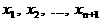 а<- корни многочлена
а<- корни многочлена 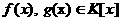 аопределяют одинаковые функции. Это означает, что
аопределяют одинаковые функции. Это означает, что 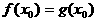 адля любого
адля любого 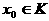
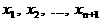
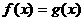
5. Делимость многочленов.
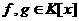 а<- многочлены степени
а<- многочлены степени 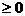 Предположим, что старший коэффициент многочлена
Предположим, что старший коэффициент многочлена  аи
аи 
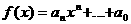



 аи
аи 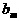 а<- единица в K. Применим индукцию по
а<- единица в K. Применим индукцию по  аи
аи 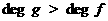
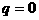

 а
а
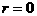 аи
аи 
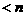 а(где
а(где 
 а(иначе возьмем
а(иначе возьмем 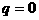 аи
аи 
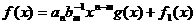
 аимеет степень
аимеет степень 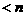
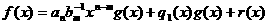 аи
аи 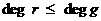
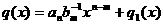
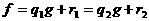
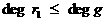 аи
аи 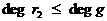
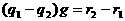
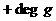
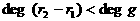
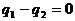
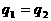 аи, следовательно,
аи, следовательно, 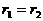
 ав кольце K, так как необходимо произвести, как следует из доказательства теоремы, деление с остатком
ав кольце K, так как необходимо произвести, как следует из доказательства теоремы, деление с остатком  аимеет степень
аимеет степень  а
а 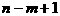 араз, чтобы получить искомые
араз, чтобы получить искомые 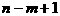 араз на
араз на 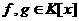 а<- многочлены степени
а<- многочлены степени 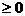
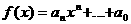
 где
где 
 так что
так что 
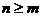 Тогда существуют однозначно определенные многочлены
Тогда существуют однозначно определенные многочлены  такие, что
такие, что 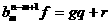 аи
аи 
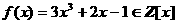 анельзя разделить на многочлен
анельзя разделить на многочлен 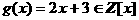 Z. Однако, многочлен
Z. Однако, многочлен 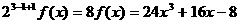 ауже можно разделить на
ауже можно разделить на



 24
24
 <-36
<-36
 <-70
<-70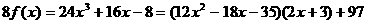
 асоответствует многочлену
асоответствует многочлену 6. Вычисление наибольшего общего делителя.
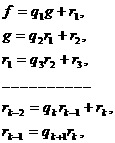 (9)
(9)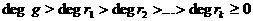
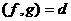
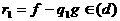

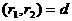
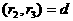 аи т.д. Таким образом,
аи т.д. Таким образом, 
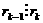


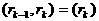
 последний ненулевой остаток (т.е. rk) и есть наибольший общий делитель многочленов
последний ненулевой остаток (т.е. rk) и есть наибольший общий делитель многочленов  амногочленов с действительными коэффициентами найдем наибольший общий делитель многочленов
амногочленов с действительными коэффициентами найдем наибольший общий делитель многочленов 
 а
а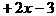

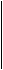
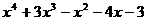
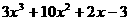





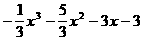

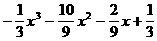
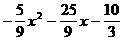
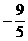
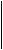
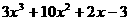
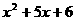




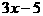



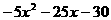
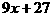



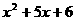
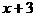


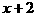

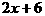

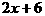

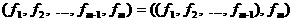 (10)
(10)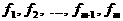
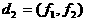
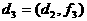 аи т.д.;
аи т.д.; 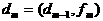 аи будет искомым наибольшим делителем.
аи будет искомым наибольшим делителем.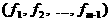 а<- это в точности общие делители многочленов
а<- это в точности общие делители многочленов 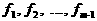
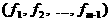 аи
аи 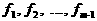 аи
аи 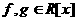 анад полем R, также всякий многочлен, кратный d, может быть представлен в виде
анад полем R, также всякий многочлен, кратный d, может быть представлен в виде 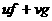
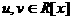 линейным выражением данного многочлена через многочлены
линейным выражением данного многочлена через многочлены 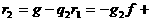 а
а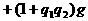

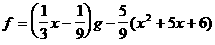
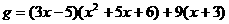
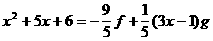 а
а  а
а
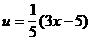
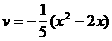


7. Наименьшее общее кратное.
 анад полем R называется многочлен
анад полем R называется многочлен 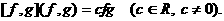 (11)
(11)
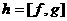

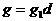 аи рассмотрим многочлен
аи рассмотрим многочлен (12)
(12)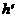 аявляется общим кратным многочленов
аявляется общим кратным многочленов 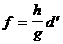
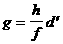 апоказывают, что
апоказывают, что  а<- общий делитель многочленов
а<- общий делитель многочленов 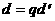
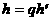
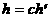
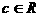
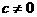
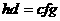
 а<- кольцо вычетов по простому модулю
а<- кольцо вычетов по простому модулю 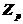
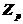 аимеется
аимеется 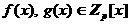 имеющие степень не выше чем
имеющие степень не выше чем 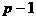 эквивалентны, то они равны.
эквивалентны, то они равны.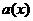 аи
аи 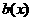 аназываются сравнимыми по многочлену
аназываются сравнимыми по многочлену 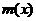
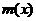 адают одинаковые остатки
адают одинаковые остатки
 аи
аи 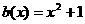 асравнимы по многочлену
асравнимы по многочлену
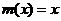
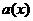 аи
аи 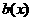

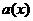 аи
аи 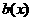 ас остатком на
ас остатком на 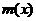
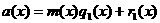
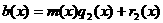
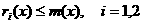

 аи разность
аи разность 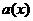
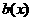
 аделится на
аделится на 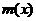

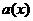
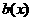
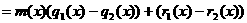 аследует, что
аследует, что 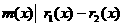

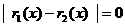


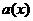
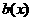
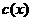
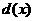

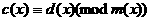 а
а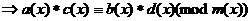
 а<- любая из операций
а<- любая из операций 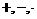 а(т.е. сравнения можно почленно складывать, вычитать и перемножать).
а(т.е. сравнения можно почленно складывать, вычитать и перемножать).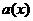
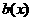
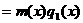
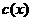
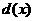
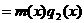
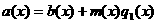
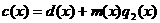
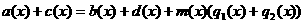
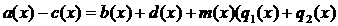

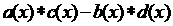 аделится на
аделится на 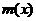 апри любой операции
апри любой операции 
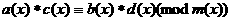
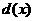 а<- общий делитель многочленов
а<- общий делитель многочленов 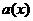 аи
аи 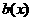

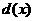 а<- общий делитель многочленов
а<- общий делитель многочленов 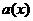
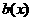
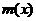 ато существуют многочлены
ато существуют многочлены 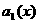
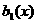
 атакие, что:
атакие, что: 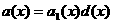


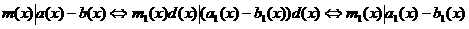
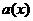 апо многочлену
апо многочлену 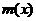
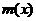 аи обозначают через
аи обозначают через 
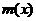 аобозначим
аобозначим 
 аоперации сложения и умножения.
аоперации сложения и умножения.
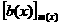
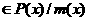 аположим:
аположим:
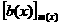


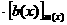
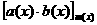

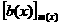 анужно выбрать из них по одному представителю, сложить (перемножить) их как многочлены и взять класс,
содержащий полученный многочлен. В определении в качестве таких представителей выбраны многочлены
анужно выбрать из них по одному представителю, сложить (перемножить) их как многочлены и взять класс,
содержащий полученный многочлен. В определении в качестве таких представителей выбраны многочлены 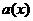 аи
аи 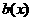

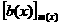 асодержится много других многочленов, и мы заранее не верены в том, что результат сложения
(умножения) классов не зависит от выбора представителей. Если бы результат зависел от выбора представителей, то складывая одни и те же классы, мы могли бы получать разные результаты. Это бы означало, что операции определены некорректно.
асодержится много других многочленов, и мы заранее не верены в том, что результат сложения
(умножения) классов не зависит от выбора представителей. Если бы результат зависел от выбора представителей, то складывая одни и те же классы, мы могли бы получать разные результаты. Это бы означало, что операции определены некорректно.


 аи по теореме 8 имеем:
аи по теореме 8 имеем: