Читайте данную работу прямо на сайте или скачайте
Стохастическая диффузионная модель гетерогенных популяций
1. Введение.
× × × × × × × × × × × × × × × × × × × ×
В данной работе мы исследуема феномен симбиоза двух неоднородных популяций клеток в словиях резкого изменения параметров окружающей среды. Популяции будем рассматривать в терминах процессов размножения и гибели.
Во многих работах были описаны модели, описывающие процессы размножения и гибели в больших однородных популяциях. Методы описания и моделирования основывались или на вероятностях перехода или на инфинитизимальных опрераторах или на так называемых компенсаторах.
Здесь мы рассмотрим процессы размножения и гибели в неоднородных популяциях в терминах метод ² случайного блуждания в случайной среде функционального типа ² (дополнение и некоторое обобщение словно-Марковского представления процессов размножения и гибели). Такое описание позволяет честь при моделировании различные параметры окружающей среды, влияющие на развитие популяций, что, несомненно, необходимо с точки зрения адекватности модели наблюдаемым явлениям.
2.Описание модели.
Итак, мы рассматриваем эволюцию двух неоднородных популяций в словиях изменения климата. В качестве параметра окружающей среды здесь выступает температура.
Пусть процесс  а- процесс со скачками,
значения которого имеюта смысл средней температуры, т.е. определяют климат. В любой момент времени t процесс
а- процесс со скачками,
значения которого имеюта смысл средней температуры, т.е. определяют климат. В любой момент времени t процесс 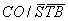 аможет принимать одно из трёх значений:
аможет принимать одно из трёх значений:  процесс
процесс 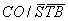 аимеет длинные промежутки постоянства, что означает стабильность климата. Скачок процесса
аимеет длинные промежутки постоянства, что означает стабильность климата. Скачок процесса
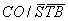 аопределяет смену климата.
аопределяет смену климата.
Описанный процесс может быть представлен в виде:
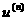 (1)
(1)
где константа  ,
,  аи
аи  анезависимые пуассоновские процессы с интенсивностью скачков
анезависимые пуассоновские процессы с интенсивностью скачков 
Рассмотрим процесс диффузионного типа  а значения температуры окружающей среды, где происходита развитие популяций:
а значения температуры окружающей среды, где происходита развитие популяций:
 (2)
(2)
где  аиза (1),
аиза (1),  а- стандартный винеровский процесс,
а- стандартный винеровский процесс,  а- коэффициент диффузии. Наличие отрицательной обратной связи с параметром
а- коэффициент диффузии. Наличие отрицательной обратной связи с параметром 
 а²отходить далеко²а от значений процесс
а²отходить далеко²а от значений процесс 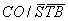
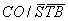
 асразу следует за изменением климата. Таким образом текущая температура колеблется около средней температуры, что соответствует действительности. Амплитуда этих колебаний определяется параметрами
асразу следует за изменением климата. Таким образом текущая температура колеблется около средней температуры, что соответствует действительности. Амплитуда этих колебаний определяется параметрами  аи
аи 
Полагаем, что в построенных климатических словиях эволюционируют две неоднородные популяции клеток  аи
аи 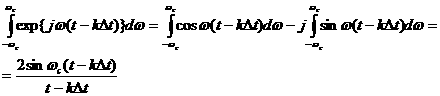
 амы разобьём на множество групп следюущим образом: интервал возможных температур
амы разобьём на множество групп следюущим образом: интервал возможных температур  а(3
а(3 а- возможные отклонения текущей температуры от средней (
а- возможные отклонения текущей температуры от средней ( аопределяется параметрами
аопределяется параметрами  аи
аи 

 авыйдет из интервала
авыйдет из интервала 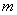 амала) разобьём на
амала) разобьём на 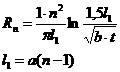 аподинтервалов длиной
аподинтервалов длиной 
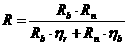
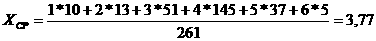
 а-а
а-а 
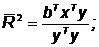

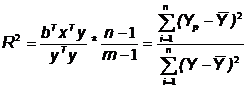 аснижается.
аснижается.
Процессы 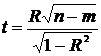 а- определяют число клеток в группе
а- определяют число клеток в группе 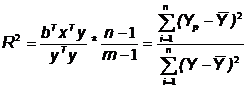
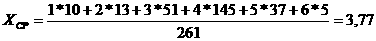
 i=1,2) :
i=1,2) :
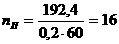 (3)
(3)
Деление клетки в группе  аопределяется скачком точечного процесса[1]
аопределяется скачком точечного процесса[1] 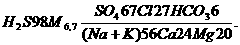

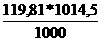 (4)
(4)
Гибель клетки в группе  аопределяется скачком точечного процесса
аопределяется скачком точечного процесса  ас компенсатором
ас компенсатором 
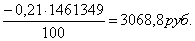 (5)
(5)
где 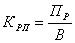 Ц неотрицательная, симметричная и монотонная на интервалах
Ц неотрицательная, симметричная и монотонная на интервалах  аи
аи  афункция (для прощения в рассматриваемой модели полагали
афункция (для прощения в рассматриваемой модели полагали 
Теперь рассмотрим развитие каждой из групп 
Предположим, что возможны следующие ситуации при делении клетки группы 
1.
с вероятностью  амогут образоваться две клетки в группе
амогут образоваться две клетки в группе 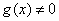
2.
ас вероятностью 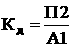 амогут образоваться две клетки в группе
амогут образоваться две клетки в группе 
3.
с вероятностью 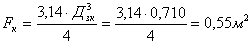 амогут образоваться две клетки в группе
амогут образоваться две клетки в группе 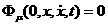
4.
с вероятностью 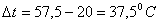 амогут образоваться две клетки в группе
амогут образоваться две клетки в группе 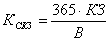
при этом 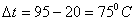
 а
а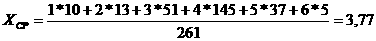
Положим 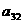
 а
а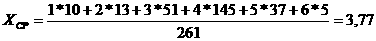
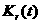 аи
аи 
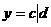

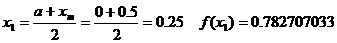
Пусть 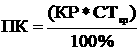
 а
а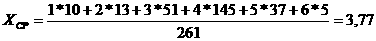 - последовательности независимых случайных величин с распределением:
- последовательности независимых случайных величин с распределением:  а"t³0, l=(1,
2, 3, 4).
а"t³0, l=(1,
2, 3, 4).
Теперь численность клеток в группе 

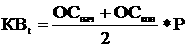 а (6)
а (6)
начальная численность группы  а-а константа.
а-а константа.
Гибель популяции определим как падение численности клеток ниже критического ровня Nкр.
При моделировании развития популяций полезно рассматривать процесс 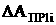
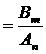 (7)
(7)
значения которого имеют смысл средней температуры благоприятной для популяции и выражают степень её адаптации к климату (чем меньше величина ½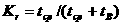 ½,
тем больше популяция i приспособлена к климату).
½,
тем больше популяция i приспособлена к климату).
3.Выбор параметров моделирования.
Положим время моделирования T равным
500. Константа А=5 и параметры 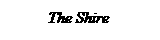 аи
аи  авыберем по правилу У3sФ (
авыберем по правилу У3sФ ( s=1), т.е. множество температур определено на интервале (-8;8),
который разделим на подинтервалы с шагом D=0.1.
s=1), т.е. множество температур определено на интервале (-8;8),
который разделим на подинтервалы с шагом D=0.1.
Начальные количества клеток в группах определим следующим образом: 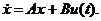 аесли
аесли  аи
аи  аесли
аесли 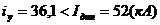
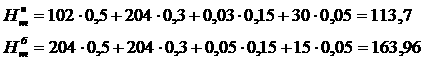 аесли
аесли 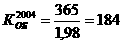 аи
аи  ав остальных случаях.
ав остальных случаях.
Критический ровень численности популяции Nкр положим равным 50.
Параметры интенсивностей процессов размножения и гибели 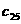 аи
аи 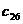 а(см. (4) и (5))
выберем следующим образом. Во-первых, заметим, что модель стойчива к изменению этих параметров и ведёт себя предсказуемо, т.е. если взять параметр рождения
а(см. (4) и (5))
выберем следующим образом. Во-первых, заметим, что модель стойчива к изменению этих параметров и ведёт себя предсказуемо, т.е. если взять параметр рождения 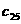
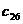 а Поэтому мы можем выбирать параметры исходя из соображения адекватности модели реальным явлениям.
а Поэтому мы можем выбирать параметры исходя из соображения адекватности модели реальным явлениям.
Выберем параметры интенсивности деления и гибели клеток популяции N 1 таким образом, чтобы численность возрастала при нормальном климате и меньшалась при его изменении.
Такая ситуация, например, возможна при значениях параметров 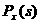

 араз ).
араз ).
Рассуждая аналогично, выберем параметры размножения и гибели для второй популяции N 2 таким образом, чтобы численность клеток меньшалась даже при нормальном климате. Это возможно при значениях параметров, например, 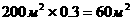
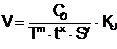
4.Компьютерное моделирование.
При компьютерном моделировании решались следующие задачи:
1. погибнут ли популяции развиваясь отдельно (т.е. при вероятности мутации клеток популяции N iа в популяцию N 3-i  аравной 0),
аравной 0),
2. выживут ли популяции развиваясь в симбиозе.
 |
Пронаблюдаем первую ситуацию: положим вектор вероятностей переход

Первая популяция погибает при изменении климата.
Y - процесс текущей температуры
Z1 - средняя температура, благоприятнапя для 1-йо популяции
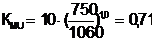 а
а
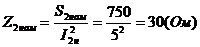
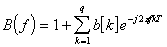 |
N1 - численность первой популяцииа
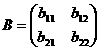 |
Рассмотрим вторую популяцию: положим вектор вероятностей перехода
Вторая популяция погибает в нормальном климате.
Y - процесс текущей температуры
Z2 - средняя температура, благоприятнапя для 1-йо популяции
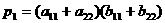

N2 Ц
 |
ачисленность второй популяции
Рассмотрим теперь эффект симбиоза двух популяций (т.е.  ).
).
Положим вектор переходных вероятностей для первой популяции 
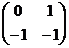
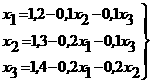 |
Развитие двух популяций в симбиозе.
 |
N1 - численность первой популяции,
N2а Ца численностьвторой популяции
Компьютерная реализация модели показала, что при раздельном развитии, т.е. при невозможности мутации клеток одной популяции в другую, популяции погибают при изменении климата (параметры модели подобраны таким образом). Однако при совместном развитии, т.е. при симбиозе, клетки популяции с высоким ровнем мутации (погибающей даже при нормальном климате) обновляют клетки популиции с низким ровнем мутации (развивающейся в нормальном климате, но погибающей при его смене) и наоборот, и это позволяет популяциям выжить в словиях смены климата.
[1] Для любого точечного процесса - процесса, траектории которого представляют собой кусочно-постоянную функцию со скачками равными 1 (например) - имеет место представление: а-а квадратично-интегрируемый локальный мартингал, и -а компенсатор процесс апредставляет собой интенсивность скачков процесса где адостаточно малая положительная величина.

