Читайте данную работу прямо на сайте или скачайте

Специальные методы решения алгебраических равнений. Решения равнений высших степеней

Одесское территориальное отделение

Малой академии наук Украины

Секция математики

Специальные методы решения алгебраических равнений.

Решения равнений высших степеней

Ученица 10-М класса

Одесской школы №20

Руководитель:

Касьян Л. Ю.

Научный руководитель

Одесса 2003

Содержание:

1.Определение алгебраического равнения.

2.История развития науки о решении алгебраических равнений.

3.Специальные методы решения алгебраических равнений.

4.Вывод.

5.Список литературы.

Известный немецкий математик Курант писал: На протяжении двух с лишним тысячелетий обладание некоторыми, не слишком поверхностными, знаниями в области математики входило необходимой составной частью в интеллектуальный инвентарь каждого образованного человека. И среди этих знаний было мение решать равнения.

Уравнение -а аналитическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Аргументы, от которых зависят эти функции, называются обычно неизвестными, значения неизвестных, при которых значения функций равны, - решениями, или корнями, уравнения. О таких значениях неизвестных говорят, что они довлетворяют данному уравнению.

Совокупность решений данного равнения зависит от области М значений, допускаемых для неизвестных. равнение может не иметь решений в М, тогда оно называется неразрешимым в области М. Если равнение разрешимо, то оно может иметь одно или несколько, или даже бесконечное множество решений. Например, равнение x⁴ - 4 = 0 неразрешимо в области рациональных чисел, но имеет два решения: x₁ = x_2а = -ав области действительных чисел и четыре решения: x₁ = =x₂ = -x₃ = i, x₄ = -iа‑ в области комплексных чисел. равнение sin x = = 0 имеет бесконечное множество решений: x_k = k, k = 0,

Если уравнение имеет решениями все числа области М, то оно называется тождеством в области М.

Два уравнения называются равносильными, если каждое решение одного равнения является решением другого, и наоборот, причём оба равнения рассматриваются в одной и той же области.

Процесс разыскания решений равнения заключается обычно в замене равнения равносильным. Замена равнения равносильным основана на применении четырёх аксиом:

1.                     Если равные величины величить на одно и тоже число, то результаты будут равны.

2.                    Если из равных величин вычесть одно и тоже число, то результаты будут равны.

3.                    Если равные величины множить на одно и тоже число, то результаты будут равны.

4.                    Если равные величины разделить на одно и тоже число, то результаты будут равны.

В некоторых случаях приходится заменять данное равнение другим, для которого совокупность корней шире, чем у данного равнения. Поэтому, если при решении уравнения делались действия, могущие привести к появлению посторонних корней, то все полученные корни преобразованного равнения проверяют подстановкой в исходное равнение.

Наиболее полно изучены алгебраические равнения. Их решение было одной из важнейших задач алгебры в 16-17 вв. равнения вида а= 0, где

= a₀xⁱyⁱ Е v^k + a₁x¹y^m Е vⁿ + a_sx^py^q Е v^r,

где x, y, Е, v - переменные, i, j, Е, r - показатели степеней (целые неотрицательные числа). Многочлен от одной переменной записывается так:

= a₀xⁿ + a₁x^n-1 + Е + a_n-1x + aⁿ.

Например, 3x⁴ - x³ + 2x² + 4x - 1. Алгебраическим равнением с одним неизвестным называется любое равнение вида а Если a₀0, то n называется степенью равнения. Например, 2x + 3 = 0 - равнение первой степени. Уравнения второй степени называются линейными. равнение второй степени называются квадратными, равнения третьей степени - кубическими. Аналогичные названия имеют и равнения более высоких степеней.

Решение линейного равнения ax + b = 0 записывается в виде x = -

Решения общего квадратного равнения ax² + bx + c = 0 можно получить с помощью формулы

x=

Таким образом, существуют два решения, которые в частном случае могут совпадать.

Явные формулы, аналогичные формуле для решения квадратного равнения, можно выписать только для равненийа только третьей и четвёртой степеней. Но и эти формулы сложны и далеко не всегда помогают легко найти корни. Что касается равнений пятой степени или выше, то для них, как доказал Н. Абель в 1824, нельзя казать общую формулу, которая выражала бы корни уравнения через его коэффициенты при помощи радикалов. В отдельных частных случаях равнения высших степеней даётся легко решить, факторизуя их левую часть, то есть разлагая её на множители.

Например, равнение x³ + 1 = 0 можно записать в виде (x + 1)(x² - x + 1) = 0. Решения мы находим, полагая каждый из множителей равным нулю:

x + 1 = 0,

x² - x + 1 = 0.

Таким образом, корни равны x = -1, 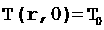, то есть всего три корня. Если равнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твёрдая веренность в том, что решение существует: алгебраическое равнение n-й степени имеет ровно n корней.

Уже в древности люди осознали, как важно научиться решать алгебраические равнения.

К ним сводятся очень многие и очень разнообразные вопросы практики и естествознания (конечно, здесь можно сразу предполагать, что a₀, так как иначе степень равнения на самом деле не n, меньше). Многим, разумеется, приходила в голову заманчивая мысль найти для любо степени n формулы, которые выражали бы корни равнения через его коэффициенты, то есть, решали бы равнение в радикалах. Однако лмрачное средневековье оказалось как нельзя более мрачным и в отношении обсуждаемой задачи - в течение целых семи столетий требуемых формул никто не нашёл! Только в 16 веке итальянским математикам далось продвинуться дальше - найти формулы для n=3 и n=4. История их открытий и даже авторства найденных формул достаточно темны по сей день, и мы не будем здесь выяснять сложные отношения между Ферро, Кардана, Тартальей и Феррари, изложим лучше математическую суть дела.

Рассмотрим сначала равнение

а₀x³ + a₁x² + a₂x + a₃ = 0.

Легко проверить, что если мы положим x = y - а, где y - новое неизвестное, то дело сведется к решению равнения

y³ + py + q = 0,

где p,q - новые коэффициенты. Счастливая догадка итальянцев состояла в том, чтобы искать y в виде суммы y = u + v,где u,v - два новых неизвестных. Для них уравнение перепишется - после небольшой перегруппировки слагаемых - так:

u³ + v³ + (3uv + p)(u + v0) + q = 0

Так как неизвестных теперь два, на них можно наложить еще какое- нибудь словие - лучше всего

3uv + q = 0,

тогда исходное равнение примет совсем простой вид

u³ + v³ + q = 0.

Это означает, что сумма кубов u³, v³ должна равняться - q, а их произведение -u³, v³ должны быть корнями квадратного равнения

t² + qt - а= 0,

для него формула же известна. В итоге получается формула

y = а+

причем из девяти пар значений входящих в нее кубических радикалов надо брать только пары, дающие в произведении Цp/3, как вытекает из нашего рассуждения. Исторически за этой формулой закрепилось название формулы Карнадо, хотя вопрос о ее авторстве так до конца и не выяснен.

Для n = 4 формулу открыл Феррари, она выглядит сложнее, но тоже использует только четыре арифметических действия и извлечение радикалов. Вот набросок вывода формулы Феррари. Прежде всего, подобно предыдущему, положим

x = y - тогда дело сведется к решению равнения вида

y⁴ + pq² + qy + r = 0.

Дополнив y⁴ до (y² + z)², т.е. прибавив и вычтя в левой части 2zy² + z², где z - вспомогательное неизвестное, получим

(y² + z)² - .

Подберем теперь z так, чтобы квадратный трёхчлен в квадратных скобках оказался полным квадратом. Для этого нужно, чтобы его дискриминант равнялся нулю, т.е. чтобы было

q² а- 4(2z - p)(z² - r) = 0.

Можем ли мы решить это равнение относительно z? Да, можем, так как оно кубическое. Пусть z₀ - какой-нибудь его корень (даваемый формулой Кардано) тогда исходное равнение перепишется в виде

y₁а = y₂ =

y₃ = y₄ =

При этом знаки перед радикалами авыбирают так, чтобы выполнялось равенство

В 1770-71 гг. знаменитый французкий математик Лагранж (1736-1819) публикует в Мемуарах Берлинской Академии свой мемуар Мысли над решением алгебраических равнений, в котором делает критический пересмотр всех решений равнений 3-й и 4-й степеней, данных его предшественникам.

Исследования Лагранжа дали для последующих алгебраистов весьма добный аппарат. Кроме того, они казали путь, по которому следовало искать доказательства невозможности общего решения уравнений в радикалах.

Дальнейшим этапом в выяснении проблемы решения равнений в радикалах послужили работы Руффини (P.Ruffini, 1765-1822) и Абеля (N.-H. Abel, 1802-1829). Руффини (1799) предложил доказательство неразрешимости в радикалах равнении 5-й степени, коэффициенты которого являются независимыми. Однако его доказательство окончилось неудачей.

Нужен был принципиально новый подход. На этот раз он не заставил себя долго ждать - же в 1824 году молодой (и в возрасте 27 лет мерший) норвежский математик Нильс Генрик Абель, опираясь на идеи Лагранжа, связанные с перестановками корней равнения, доказал, что требуемых формул, которые решали бы в радикалах равнение решали бы в радикалах уравнение общего вида, при n5 действительно не существует. Теорема Абеля дала отрицательны ответ только для равнений общего вида, т.е. с буквенными коэффициентами а₀, а₁, Е, а_n, но, разумеется, многие конкретные уравнения сколь годно высокой степени вполне могут решаться в радикалах (пример: равнение x⁹⁰ + 5x⁴⁵ + 7 = 0). Поэтому сразу же встал вопрос о полном решении задачи - нахождении критерия разрешимости равнений в радикалах, т.е. необходимого и достаточного словия, которое по коэффициентам а₀, а₁, Е, а_n любого заданного равнения позволяло бы судить, решается равнение в радикалах или нет.

Вопрос о разрешимости равнений в радикалах был окончательно разобран, во всяком случае, принципиально, в работах Галу (Evariste Galois, 1811-1832). За свою короткую жизнь Галу спел создать теорию, которая до сих пор стоит в фокусе математической мысли. Рассматривая численные равнения, он становил понятие их группы, т.е. совокупности таких подстановок между их корнями, которые не нарушают рациональных соотношений между ними. Эта группа определяет для каждого уравнения алгебраическую структуру его корней. В частности, равнение разрешимо в радикалах тогда и только тогда, если его группа принадлежит к числу так называемых разрешимых групп. Таким образом вопрос о разрешимости каждого данного равнения в радикалах может быть решен при помощи конечного числа действий.

Обратимся теперь к исходному объекту исследования - равнению

а₀xⁿ + a₁x^n-1 + Е + a_n = 0,

где а₀, а₁, Е, а_n - заданные числа. Еще Гаусс в конце 18 века доказал лосновную теорему алгебры, гласящую, что при любых а₀, а₁, Е, а_n данное равнение имеет в поле комплексных чисел n корней, точнее, стоящий в его левой части многочлен аможет быть разложен на линейные множители

а_0,

где а₁ Е а_n - некоторые комплексные числа (называемые корнями равнения). Задача состоит в том, чтобы знать, существуют ли формулы, выражающие корни а₁, Е, а_n через коэффициенты а₀, а₁, Е, а_n c помощью четырех арифметических действий и извлечения радикалов?

Эварист Галу доказал, что общее уравнение степени nанеразрешимо в радикалах. Шестьдесят страниц, написанных накануне роковой дуэли, явились одним из истоков современной теории групп - основного и наиболее развитого раздела алгебры, изучающего в общем виде глубокую закономерность реального мира - симметрию.

Рассмотрим на примерах некоторые способы решения алгебраических равнений степени n.

Пример 1. Решить равнение

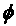
Разложим левую часть равнения на множители

Переносим

тогда

2x + 2 = 0 или Ц3x² - 6x + 24 = 0. Решая эти равнения, получаем корни

x₁ = -1, x₂ = -4, x₃ = 2.

Разложение на множители позволило свести решение кубического равнения к решению квадратного и линейного уравнений.

Пример 2. Решить равнение

Разделим обе части равнения на а(

тогда

Пусть атогда 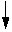Получим равнение

а

По теореме Виета корни равнения: Значит,

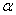
Решая эти равнения, находим корни

аа

Введение замены позволяет понизить степень равнения и свести его к решению квадратного равнения.

Пример 3. Решить равнение

Заменим это равнение равносильным ему прибавлением и вычитанием одного и того же выражения

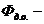
Разложим числитель на множители

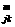
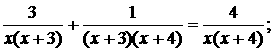
корнями которого являются

Это равнение можно решить другим способом, выполнив деление многочлена на многочлен

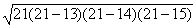
Получим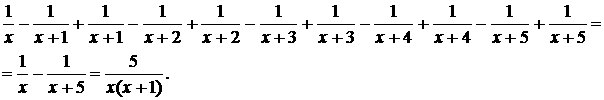

Пример 4. Решить равнение

Разделив обе части равнения на а(ане является решением данного равнения).

Полагая

корнями которого являются

Значит, аили R, корни второго

Данный пример показывает, что деление обеих частей равнения на одно и то же выражение с последующим введением замены позволяет понизить степень равнения.

Пример 5. Решить равнение

Областью допустимых значений данного равнения являются все числа, довлетворяющие словию

Тогда,

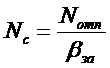
Пусть

Решая данное дробно-рациональное уравнение, получим корни

Значит,

аили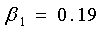

Решениями равнений являются

Пример 6. Решить равнение

ОДЗ: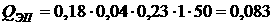

Пусть

Выполняя преобразования, данное уравнение приводится к виду

Корни этого равнения аследовательно,

Рассмотренные примеры показывают основные способы решения алгебраических равнений степени n: разложение многочлена на множители, деление на одно и тоже выражение, введение новой переменной. Все казанные способы позволяют понизить степень равнения и свести решение данного равнения к решению квадратного или линейного равнения.

Истоки алгебры восходят к глубокой древности. же около 4 лет назад вавилонские ченые владели решением квадратного равнения и решали системы двух равнений, из которых одно - второй степени. С помощью таких равнения решались разнообразные задачи землемерия, архитектуры и военного дела. Точный язык математики позволяет просто выразить факты и соотношения, которые, будучи изложенными обычным языком, могут показаться запутанными и сложными. Неизвестные величины, обозначаемые в задаче символами, например x, можно найти, сформулировав задачу на математическом языке в виде равнений. Методы решения равнений составляют в основном предмет того раздела математики, который называется алгеброй и теорией чисел. ниверсальной формулы для нахождения корней алгебраического равнения n - ой степени нет. В данной работе на конкретных примерах рассмотрели различные способы понижения степени равнения.

Список использованной литературы:

1.Математическая энциклопедия, том 5.

2.Тумаркин Л.А. У История математики У, М., 1975.

3.Кизнер Ф.И. Основные понятия математики, М., 1987

4.Смонов А.Я. Конкурсные задачи по математике, М., 1991