Читайте данную работу прямо на сайте или скачайте
Поиск максимальных потоков в сетях
Министерство образования и науки Украины
Луганский национальный педагогический ниверситет имени Тараса Шевченко
Кафедра алгебры и дискретной математики
Киршта Александр Михайлович
Магистерская работа по специальности 8.080101
Математика
Научный руководитель Ц
к.ф.-м.н., доцент
Михайлова И.А.
Луганск - 2006 г.
Содержание
Введени.3
Раздел I. Основные понятия и определения теории графов..6
1.1. Понятие графа.6
1.2. Графическое представление графов.7
1.3. Виды графов7
1.4. Элементы графов8
1.5. Представление графов с помощью матриц..9
1.5.1. Матрицы инцидентности и списки рёбер...9
1.5.2. Матрицы смежности.12
Раздел II. Потоки в сетях..14
2.1. Понятие сети14
2.2. Задача о максимальном поток..16
2.3. Алгоритм размещения пометок для задачи о максимальном поток16
2.4. Алгоритм Форда-Фалкерсона18
2.5. Граф со многими источниками и стоками22
2.6. Задача о многополюсном максимальном поток24
Раздел. Автоматизация поиска максимальных потоков в сетях29
3.1. Описание интерфейса программы.29
3.2. Инструкция пользователя30
3.3. Реализация программы33
3.4. Описание программного кода38
Выводы40
Литература.41
Приложени43
ВВЕДЕНИЕ
Начало теории графов все единодушно относят к 1736 г., когда Эйлер не только решил популярную в то время задачу о кенигсбергских мостах, но и нашёл критерий существования в графе специального маршрута (эйлерова цикла, как теперь его называют). Однако этот результат более ста лет оставался единственным результатом теории графов. Лишь в середине XIX века инженер-электрик Г.Кирхгофф разработал теорию деревьев для исследования электрических цепей. А математик А. Кэли в связи с описанием строения углеводородов решил перечислительные задачи для трёх типов деревьев. К этому же периоду относится появление знаменитой проблемы четырёх красок.
Родившись при решении головоломок и занимательных игр (задачи о шахматном коне, о ферзях, кругосветное путешествие, задачи о свадьбах и гаремах и т. п.), теория графов в настоящее время стала простым, доступным и мощным средством решения вопросов, относящихся к широкому кругу проблем. В виде графов можно, например, интерпретировать схемы дорог и электрические цепи, географические карты и молекулы химических соединений, связи между людьми и группами людей.
За последние десятилетия теория графов превратилась в один из наиболее бурно развивающихся разделов математики. Это вызвано запросами стремительно расширяющейся области приложений. В теоретико-графовых терминах формулируется большое число задач, связанных с дискретными объектами. Рассмотрим примеры некоторых практических задач.
1. Транспортные задачи, в которых вершинами графа являются пункты, ребрами - дороги (автомобильные, железные и др.) или другие транспортные (например, авиационные) маршруты. Другой пример - сети снабжения (энергоснабжения, газоснабжения, снабжения товарами и т.д.), в которых вершинами являются пункты производства и потребления, ребрами - возможные маршруты перемещения (линии электропередач, газопроводы, дороги и т.д.). Соответствующий класс задач оптимизации потоков грузов, размещения пунктов производства и потребления и т.д., иногда называется задачами обеспечения или задачами о размещении. Их подклассом являются задачи о грузоперевозках.
2. Технологические задачи, в которых вершины отражают производственные элементы (заводы, цеха, станки и т.д.), дуги - потоки сырья, материалов и продукции между ними, заключаются в определении оптимальной загрузки производственных элементов и обеспечивающих эту загрузку потоков.
3. Обменные схемы, являющиеся моделями таких явлений как бартер, взаимозачеты и т.д. Вершины графа при этом описывают частников обменной схемы (цепочки), дуги - потоки материальных и финансовых ресурсов между ними. Задача заключается в определении цепочки обменов, оптимальной с точки зрения, например, организатора обмена и согласованной с интересами частников цепочки и существующими ограничениями.
4. правление проектами. С точки зрения теории графов проект - совокупность операций и зависимостей между ними. Хрестоматийным примером является проект строительства некоторого объекта. Совокупность моделей и методов, использующих язык и результаты теории графов и ориентированных на решение задач правления проектами, получила название календарно-сетевого планирования и правления (КСПУ). В рамках КСПУ решаются задачи определения последовательности выполнения операций и распределения ресурсов между ними, оптимальных с точки зрения тех или иных критериев (времени выполнения проекта, затрат, риска и др.).
5. Модели коллективов и групп, используемые в социологии, основываются на представлении людей или их групп в виде вершин, отношений между ними (например, отношений знакомства, доверия, симпатии и т.д.) - в виде ребер или дуг. В рамках подобного описания решаются задачи исследования структуры социальных групп, их сравнения, определения агрегированных показателей, отражающих степень напряженности, согласованности взаимодействия, и др.
6. Модели организационных структур, в которых вершинами являются элементы организационной системы, ребрами или дугами - связи (информационные, правляющие, технологические и др.) между ними.
Изучение этих и других подобных им практических задач приводит к теории потоков в сетях. В данной работе рассматривается только одна (но наиболее существенная) задача этой теории, именно задача нахождения максимального потока.
1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕОРИИ
Пусть V - непустое множество, V (2) Ц множество всех его двухэлементных подмножеств. Пара (V, E), где Е - произвольное подмножество множества V (2), называется графом (неориентированным графом).
Элементы множества V называются вершинами графа, элементы множества Е - рёбрами. Множество вершин и рёбер графа G обозначаются символами VG и EG соответственно. Число |VG| вершин графа G называются его порядком и обозначаются через |G|. Если |G| = n, |EG| = m, то G называют (n,m)-графом.
Две вершины u и v графа смежны, если множество {u, v} является ребром, и не смежны в противном случае. Если e = {u, v} - ребро, то вершины u и v называют его концами. Такое ребро обозначают uv.
Два ребра называются смежными, если они имеют общий конец.
Вершина v и ребро e называются инцидентными, если v является концом ребра e (т.е. e = uv), и не инцидентными в противном случае.
Множество всех вершин графа G, смежных с некоторой вершиной v, называется окружением вершины v и обозначается через N(v).
Упорядоченная пара вершин называется ориентированным ребром.
Ориентированный граф (или орграф) - это пара (V, A), где V - множество вершин, А - множество ориентированных рёбер, которые называются дугами, А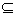 V2. Если а = (v1, v2) - дуга, то вершины v1 и v2 называются её началом и концом соответственно. Если граф ориентированный, его обозначают
V2. Если а = (v1, v2) - дуга, то вершины v1 и v2 называются её началом и концом соответственно. Если граф ориентированный, его обозначают 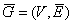
Каждому неориентированному графу можно поставить в соответствие ориентированный граф с тем же самым множеством вершин, в которых каждое ребро заменено двумя ориентированными рёбрами, которые инцидентны тем самым вершинам и имеют обратные направления. Такое соответствие будем называть каноничным.
Если у ребра начало и конец совпадают, то такое ребро называют петлёй.
1.2. Графическое представление графов
Графы добно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. При этом точки соответствуют вершинам графа, соединяющие пары точек линии (прямолинейные либо криволинейные) - рёбрам (табл.1).
Таблица 1
|
Элементы графов |
Геометрические элементы |
|
1. v Î VЦ вершина |
1. Х - точка в пространстве. |
|
2. {u,v} Ц ребро неориентированного графа |
2. uХ−Хv - отрезок. |
|
3. (v1,v2) - дуги в ориентированном графе |
3. v1Х→v2 - направленный отрезок. |
|
4. {v,v} Ц петля |
4. |
1.3. Виды графов
Множество рёбер Е аможет быть пустым (рис. 1.1). Такой граф называется нуль-графом и обозначается Ø.

рис. 1.1. Нуль-граф
Если же множество вершин V - пустое, то пустым является также множество Е. Такой граф называется пустым.
Линии, которые изображают арёбра графа,
могут пересекаться, но точки пересечения не являются вершинами (рис. 1.2, а);
разные рёбра могут быть инцидентными одной и той же паре вершин (рис. 1.2, б),
такие рёбра называются кратными. Этот случай соответствует наличию нескольких одинаковых пар (vi,vj)
 аE(G). Граф, который содержит кратные рёбра, называется мультиграфом. Ребро может соединять некоторую вершину саму с собою (рис. 1.2, в), такое ребро называется петлёй. Этот случай соответствует наличию в множестве Е пар вида (v,v). Граф с петлями и кратными рёбрами называется псевдографом. Конечный неориентированный граф без петель и кратных рёбер называется обычным.
аE(G). Граф, который содержит кратные рёбра, называется мультиграфом. Ребро может соединять некоторую вершину саму с собою (рис. 1.2, в), такое ребро называется петлёй. Этот случай соответствует наличию в множестве Е пар вида (v,v). Граф с петлями и кратными рёбрами называется псевдографом. Конечный неориентированный граф без петель и кратных рёбер называется обычным.

 |
 |
б в
Рисунок 1.2. Графы: а) - обычный, б) - с кратными рёбрами, в) - с петлёй
1.4. Элементы графов
Путь - это последовательность рёбер e1, e2, Е, em, такая, что рёбра ei, ei+1 имеют общую вершину. Число рёбер называется длинной пути. Если ни одна из вершин не появляется больше одного раза, то путь называется простым. Понятно, что в простом пути ни одно ребро не используется дважды.
Путь называется циклом, если его начальная вершина совпадает с конечной; простым циклом, если это не выполняется для других вершин.
Чередующаяся последовательность v1, e1, v2, e2, Е, el,vl+1 вершин и рёбер графа, такая, что ei = vivi+1 (i = 1, l), называется маршрутом. Если v1 =а vl+1, то маршрут замкнутый, иначе открытый.
Маршрут называется цепью,
если все его рёбра различны, и простой цепью,
если все вершины, кроме, возможно, крайних, различны. В цепи  авершины v0
и vk называются концами цепи. Цепь, которая соединяет вершины vi
и vj, обозначается
авершины v0
и vk называются концами цепи. Цепь, которая соединяет вершины vi
и vj, обозначается 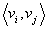
Для орграфов цепь называется путём, цикл - контуром.
Две вершины в графе называются связными, если существует соединяющая их (простая) цепь. Граф, у которого все вершины связны, называется связным. Ориентированный граф называется сильно связным, если для любых двух вершин существует ориентированный путь, который соединяет их.
1.5. Представление графов с помощью матриц
1.5.1. Матрицы инцидентности и списки рёбер
Задать граф, значит,
задать множество его вершин и рёбер, также отношение инцидентности. Когда граф G - конечный, для описания его вершин и рёбер достаточно их занумеровать. Пускай v1, v2,Е,
vn - вершины графа G; e1,
e2,Е, em - его рёбра. Отношение инцидентности можно обозначить матрицей 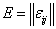 m
строк и n столбцов. Столбцы соответствуют вершинам графа, строки - его рёбрам. Если ребро е является инцидентным вершине vj, то
m
строк и n столбцов. Столбцы соответствуют вершинам графа, строки - его рёбрам. Если ребро е является инцидентным вершине vj, то 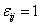
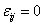 G, являющаяся одним из способов его определения (для графа на рис. 1.3), она задана в табл. 2, а.
G, являющаяся одним из способов его определения (для графа на рис. 1.3), она задана в табл. 2, а.

Рис. 1.3. Обычный граф
В матрице инцидентности 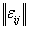 аориентированного графа
G, если вершина vj - начало ребра ei,
то
аориентированного графа
G, если вершина vj - начало ребра ei,
то  vj
Ц конец ei, то
vj
Ц конец ei, то 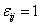 ei - петля, vj - инцидентная ей вершина,
ei - петля, vj - инцидентная ей вершина, 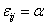
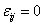 а(пример - табл. 2, б для графа рис. 1.4).
а(пример - табл. 2, б для графа рис. 1.4).

Рис. 1.4. Ориентированный граф
Таблица 2
 |
 |
||
б
В каждой строке матрицы инцидентности для неориентированного или ориентированного графа только два элемента отличны от нуля (или один, если ребро является петлёй). Потому такой способ задания графа не достаточно экономный. Отношение инцидентности можно задать ещё списком рёбер графа. Каждая строка этого списка соответствует ребру, в нём записаны номера вершин, инцидентных ему. Для неориентированного графа порядок этих вершин в строке произвольный, для ориентированного первым записывается номер или другое наименование начала ребра, другим - его конца. В таблице 3, и б приведены списки рёбер для графов, изображённых на рис. 1.3 и 1.4.
По списку рёбер графа можно легко определить матрицу инцидентности. Действительно, каждая строка этого списка соответствует строке матрицы с тем же номером. Для неориентированного графа в строке списка записываются номера элементов строки матрицы инцидентности, которые равняются 1, для ориентированного графа в этой строке первым записывается номер элемента строки матрицы, который равен -1, вторым - номер элемента, который равен 1.
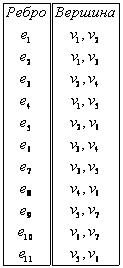 |
 |
||
Таблица 3
б
1.5.2. Матрицы смежности
Матрица смежности графа - это квадратная матрица 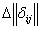 δij
равняется количеству рёбер, инцидентных i-й та j-й вершинам, для ориентированного графа этот элемент матрицы смежности соответствует количеству рёбер с началом в
-й вершине и концом в j-й. Таким образом, матрица смежности неориентированного графа симметрична (δij
= δji), ориентированного - необязательно. Если она всё-таки симметрична, то для каждого ребра ориентированного графа существует ребро, которое соединяет те же авершины, но направлено в противоположную сторону. Очевидно, ориентированный граф с симметричной матрицей смежности канонично соответствует неориентированному графу, который имеет ту же матрицу смежности.
δij
равняется количеству рёбер, инцидентных i-й та j-й вершинам, для ориентированного графа этот элемент матрицы смежности соответствует количеству рёбер с началом в
-й вершине и концом в j-й. Таким образом, матрица смежности неориентированного графа симметрична (δij
= δji), ориентированного - необязательно. Если она всё-таки симметрична, то для каждого ребра ориентированного графа существует ребро, которое соединяет те же авершины, но направлено в противоположную сторону. Очевидно, ориентированный граф с симметричной матрицей смежности канонично соответствует неориентированному графу, который имеет ту же матрицу смежности.
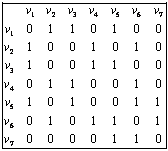
Матрицы смежности рассмотренных выше графов (см. рис. 1.3 и 1.4) приведены в таблице 4.
Матрица смежности полностью определяет соответствующий неориентированный или ориентированный граф. Число его вершин равняется размерности матрицы n, i-й и j-й вершинам графа инцидентны 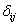 аребер. Для неориентированного графа
аребер. Для неориентированного графа 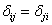
 |
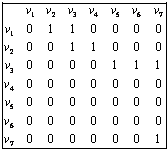 |
Таблица 4
б
Количество их равняется сумме 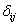 ав этом треугольнике,
то есть
ав этом треугольнике,
то есть 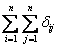
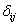 аматрицы смежности. В обоих случаях с помощью матрицы смежности легко строится, например, список ребер, который определяет граф. Элементу матрицы смежности, расположенном в -й строке и j-м столбце, соответствует
аматрицы смежности. В обоих случаях с помощью матрицы смежности легко строится, например, список ребер, который определяет граф. Элементу матрицы смежности, расположенном в -й строке и j-м столбце, соответствует 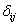 астрок списка ребер
(при
астрок списка ребер
(при 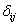 , j. Для неориентированного графа эти строки соответствуют только элементам названного выше верхнего правого треугольника матрицы смежности, то есть элементам
, j. Для неориентированного графа эти строки соответствуют только элементам названного выше верхнего правого треугольника матрицы смежности, то есть элементам
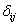 ас
ас 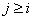
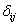
Итак, граф можно представить разными способами. Он может быть изображён на рисунке, задан матрицей инцидентности, списком рёбер или матрицей смежности. Графический вид зависит от формы линий и взаимного расположения вершин. Вид матриц и списка рёбер зависит от нумерации вершин и рёбер графа.
2. ПОТОКИ В СЕТЯХ
Сетью будем называть ориентированный связный граф без петель и параллельных рёбер. Потоки в неориентированных графах можно изобразить в виде потоков в соответствующих ориентированных. Поток в петле не влияет на распределение потока между вершинами. Рассмотрим сеть G = (V, E), |V |
= n, |E| = m. Пускай каждой дуге еj  аE поставлено в соответствие неотрицательное действительное число сj , которое назовём пропускной способностью дуги еj. Обозначим через vi → V множество дуг, выходящих из вершины vi, через V → vi - множество дуг, заходящих в вершину
vi.
аE поставлено в соответствие неотрицательное действительное число сj , которое назовём пропускной способностью дуги еj. Обозначим через vi → V множество дуг, выходящих из вершины vi, через V → vi - множество дуг, заходящих в вершину
vi.
Потоком в сети G из вершины vs в вершину vt величины
w называется неотрицательная,
определенная на дугах еj, функция φ: Е → R+ 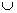 а{0}, такая, что
а{0}, такая, что
 Ц
Ц 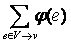 а= а
а= а (1)
(1)
φ(еj) ≤ cj, j = 1, Е, m.
Вершина vs называется источником, вершина vt - стоком, остальные вершины - промежуточными злами. Число Q(vi) = 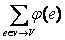 а-
а- 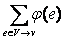 аназывается чистым потоком из вершины vi относительно φ. Число φ(е)
называется потоком по дуге е. Если реальный поток по дуге отрицательный, то его можно сделать положительным, выбрав соответствующую ориентацию дуги e. Систему равнений (1) можно переписать в векторном виде:
аназывается чистым потоком из вершины vi относительно φ. Число φ(е)
называется потоком по дуге е. Если реальный поток по дуге отрицательный, то его можно сделать положительным, выбрав соответствующую ориентацию дуги e. Систему равнений (1) можно переписать в векторном виде:
ВФ = l, (2)
где В - матрица инцидентной размерности n  аm, Ф = (φ(e1) Е φ(em))T, l = (0..0w0..0 - w0..0)T. Поскольку ранг матрицы инциденций равен n - 1, то система равнений (1) избыточна:
аm, Ф = (φ(e1) Е φ(em))T, l = (0..0w0..0 - w0..0)T. Поскольку ранг матрицы инциденций равен n - 1, то система равнений (1) избыточна: 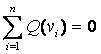 φ из vs в vt величины
w есть поток величины -w из vt в vs.
φ из vs в vt величины
w есть поток величины -w из vt в vs.
Пример

Рис. 2.1. Поток величины 3
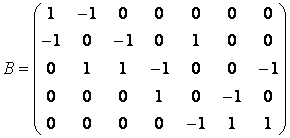
Сеть, изображённая на рис. 2.1, состоит из пяти злов и восьми дуг. Будем рассматривать поток от v1 до v5. Каждой дуге приписаны два числа: первое - величина потока по дуге, второе - пропускная способность дуги. Величина этого потока равна 3. Действительно,
Q(v1) = 5 - 2 = 3,
Q(v2) = 7 - (5 + 2) = 0,
Q(v3) = Ц4 - 0 +2 + 2 = 0, (3)
Q(v4) = Ц4 + 4 = 0,
Q(v5) = 4 + 0 - 7 = Ц3.
Систему равнений (3) можно записать в векторном виде ВФ = l (2):

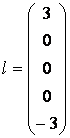
2.2. Задача о максимальном потоке
На практике часто возникает проблема определения максимальной проводимости некоторой реальной сети: сети транспортной, сети ЭВМ, других. Иногда нужно определить самый дешёвый поток и т.д. Все эти и многие другие задачи решаются с помощью алгоритмов, которые работают на сетях. Так, алгоритм о максимальном потоке ищет максимально возможную пропускную способность сети, алгоритм минимальной стоимости - самый дешёвый поток. В данном разделе будем рассматривать задачу о максимальном потоке.
Задача заключается в нахождении такого множества потоков по дугам, чтобы величина Q(vs) была максимальной.
Разрез S отделяет vs от vt,
если вершины vs, vt
принадлежат разным сторонам разреза: vs  аVs, vt
аVs, vt  аVt, V = Vs
аVt, V = Vs 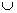 аVt.
Пропускной способностью с(S) разреза S называется сумма пропускных способностей дуг разреза, которые начинаются в Vs и заканчивается в Vt:
аVt.
Пропускной способностью с(S) разреза S называется сумма пропускных способностей дуг разреза, которые начинаются в Vs и заканчивается в Vt:
с(S) = 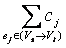 а.
а.
2.3. Алгоритм размещения пометок для задачи о максимальном потоке
лгоритм размещения пометок основан на следующей теореме.
Теорема 1.Теорема про максимальный поток и минимальный разрез. Для произвольной сети максимальная величина потока из vs в vt равняется минимальной пропускной способности разреза, который отделяет vs от vt.
Доказательство
Покажем, что величина w произвольного потока φ не превышает пропускной способности разреза (Vs,Vt), который отделяет vs от vt. Поскольку функция φ поток, то она довлетворяет равнению (1) сохранении потока:
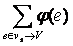 а-
а-  а= w,
а= w,
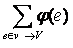 а-
а-  а= 0, v
а= 0, v  s, v t, (2)
s, v t, (2)
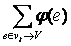 а-
а- 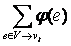 а= -w.
а= -w.
Сложим те равнения из
(2), которые соответствуют вершинам из Vs.
Учитывая, что vs  аVs, vt
аVs, vt  аVt,
получаем:
аVt,
получаем:
w = 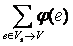 а-
а- 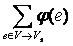 а.
а.
Всё множество вершин распадается на две стороны: V = Vs 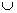 аVt.
Получаем
аVt.
Получаем
w =  а-
а- 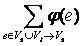 а=
а=
= 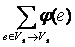 а+
а+ 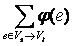 а-
а- 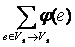 а-
а-  а=
а=
= 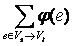 а-
а-  а≤
а≤ 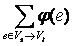 а≤
а≤ 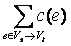 а= c(Vs, Vt).
а= c(Vs, Vt).
Теперь нужно показать, что существуют некоторые поток φ и разрез (Vs, Vt), для которых величина потока равняется пропускной способности разреза. Как видно, все потоки от Vs до Vt ограничены и среди них можно выбрать максимальный поток φ. С её помощью определим разрез (Vs, Vt), для которого
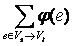 а= c(Vs,
Vt),
а= c(Vs,
Vt),  а= 0.
а= 0.
Определим множество Vs рекуррентно:
1) vs  аVs.
аVs.
2) Если, vs  аVs адуга e
идёт из вершины vi в какую-либо вершину vj и φ(e) < c(e), то vj
аVs адуга e
идёт из вершины vi в какую-либо вершину vj и φ(e) < c(e), то vj  аVs.
аVs.
3) Если vi  аVs,
дуга e идёт из вершины vr
в вершину vi и φ(e), то vj
аVs,
дуга e идёт из вершины vr
в вершину vi и φ(e), то vj  аVs.
аVs.
Шаг 1)
построения множества Vs
означает, что источник vs
принадлежит построенной стороне разреза. Покажем, что сток тогда лежит на другой стороне разреза - vt  аVt = V/Vs.
Допустим противоположное: пусть vt
аVt = V/Vs.
Допустим противоположное: пусть vt
 аVs.
Тогда существует неориентированная цепь, которая идёт из источника vs в сток vt, такая, что для каждой дуги ei цепи с направлением,
совпадающим с ориентацией от источника к стоку
аVs.
Тогда существует неориентированная цепь, которая идёт из источника vs в сток vt, такая, что для каждой дуги ei цепи с направлением,
совпадающим с ориентацией от источника к стоку 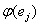 а> 0.
а> 0.
Обозначим через l1 = min{c(ej) - c(ei)} все дуги ei цепи с направлением, совпадающим с ориентацией от источника к стоку, l2 = min{φ(ei)} все дуги ei цепи с направлением, не совпадающим с ориентацией от источника к стоку, l = min(l1, l2). Поток φ можно величить на l, величив на l поток на дугах цепи, ведущих от стока к источнику. Это противоречит тому, что величина потока φ максимальная величина допустимого потока из вершины vs в вершину vt.
2.4. Алгоритм Форда-Фалкерсона
Доказательство теоремы 1 даёт алгоритм для построения минимального разреза (Vs, Vt), который отделяет vs от vt, и максимальный поток φ от vs до vt. Этот алгоритм был предложен Л. Фордом и Д. Фалкерсоном. Алгоритм начинает работу с известного допустимого потока φ (например, с нулевого). Потом расчеты развиваются в виде последовательности расстановки пометок (операция А), каждая из которых приводит к потоку с большей величиной (операция Б), или же завершается выводом, что рассмотренный поток максимален.
Будем предполагать, что пропускные способности cj дуг сети целые числа.
Операция А (расстановка пометок). Каждая вершина может находиться в одном из трёх состояний: вершине приписана пометка и вершина просмотрена (то есть она имеет пометку и все смежные с ней вершины обработаны), вершина помечена, но не просмотрена, вершина не помечена. Пометка вершины vi имеет один из двух видов: (+vj, l) или (-vj, l). Часть +vj пометки первого типа показывает, что поток допускает величение вдоль дуги (vj, vi) на величину l. Часть -vj пометки второго типа показывает, что поток допускает меньшения вдоль дуги (vi, vj) на величину l. Сначала все вершины не имеют пометок.
Шаг 1.
Источнику vs присваивается пометка (+,
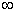 vs помечена, но не просмотрена.
vs помечена, но не просмотрена.
Шаг 2.
Возьмём произвольную помеченную, но не просмотренную вершину. Пусть оно имеет пометку ( vr, l(vj)). Просмотрим её, то есть просмотрим все вершины, смежные с ней, и пометем те из них, которые не помечены.
vr, l(vj)). Просмотрим её, то есть просмотрим все вершины, смежные с ней, и пометем те из них, которые не помечены.
Всем непомеченным вершинам vj, в которые входят дуги er из vi и для которых φ(еr) < cr, приписываем пометку (+vi, l(vj)), где l(vj) = min(l(vi)), cr - φ(еr)).
Всем непомеченным вершинам vj, из которых выходят дуги er в xi и для которых φ(er) > 0, приписываем пометку (-vi, l(vj)), где l(vj) = min(l(vi)), φ(еr)).
Теперь вершина vi и помечена, и просмотрена, вершина аvj, помечена, но не просмотрена.
Шаг 3. Повторять шаг 2 до тех пор, пока или сток - вершина vt - будет помечена, или вершина vt будет не помечена и никаких других пометок нельзя будет расставить. В первом случае переходим к операции Б, во втором случае алгоритм заканчивает работу с максимальным потоком φ. Во втором случае множество помеченных и множество непомеченных вершин образовывают две стороны минимального сечения (Vs, Vt).
Операция Б (увеличения потока)
Шаг 4. Принять v = vt и перейти к шагу 5.
Шаг 5. Если пометка в вершине v имеет вид (+z, l(v)), то изменить поток вдоль дуги (z, v) с φ(z, v) на φ(z, v) + l(v).
Если пометка в вершине v имеет вид (-z, l(v)), то изменить поток вдоль дуги (v, z) с φ(v, z) на φ(v, z) - l(v).
Шаг 6. Если z = vs, то стереть все пометки и вернуться к шагу 1, чтобы снова начать расставлять пометки, но, используя же лучшенный поток, который найден на шаге 5.
Если z ≠ vs, то взять v = z и вернуться к шагу 5.
Рассмотрим на примере работу алгоритма Форда-Фалкерсона.
1. Возьмём поток, изображённый на рисунке 2.1 как начальный допустимый поток. Он имеет величину 3.
2.
Присвоим источнику, вершине v1,
пометку (+, 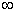 v1
помечена, но не просмотрена.
v1
помечена, но не просмотрена.
3. Просмотрим вершины, смежные с вершиной v1. Вершине v2 присвоим пометку (+v1, 1), а вершине v3 - пометку (-v1, 2) (φ(v1, v2) = 5 < 6 = c1, φ(v3, v1) = 2 > 0). Вершина v1 помечена и просмотрена, вершины v2 и v3 помечены, но не пересмотрены.
4. Пересмотрим вершины, смежные с вершиной v3. Из вершин, смежных с вершиной v3, не помечены вершины v4 и v5. Вершине v4а присвоим пометку (-v3, 2), поскольку φ(v4, v3) = 4 > 0 и min(2, 4) = 2. Вершину v5а не помечаем, поскольку φ(v5, v3) = 0.
5. Просмотрим вершины, смежные с вершиной v2. Вершине v5а присвоим пометку (+v2, 1), поскольку φ(v2, v5) = 7 < 8 = c5. Сток помечен. Переходим к операции В - величения потока.
6. Сток имеет пометку (+v2, 1). Поэтому увеличиваем поток вдоль дуги (v2, v5) на 1.
7. Вершина v2 имеет пометку (+v1, 1). Поэтому величиваем поток авдоль дуги (v1, v2) на 1. Мы получили новый поток величины 4 (рис. 2.2).

Рис. 2.2. Поток величины 4
8. Стираем все пометки.
9. Присваиваем вершине v1 пометку (+, 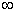
10. Пересматриваем вершины, смежные с вершиной v1. Вершине v3 присваиваем пометку (-v1, 2). Вершину v2 не помечаем, так как φ(v1, v2) = 6 = c(y1).
11. Пересмотрим вершины, смежные с вершиной v3. Вершине v4 присвоим пометку (-v3, 2), поскольку φ(v4, v3) = 4 > 0, l(v3) = 2 и min(2, 4) = 2.
12. Пересмотрим вершины, смежные с вершиной v4. Вершине v5 присвоим пометку (-v4, 2), так как φ(v5, v4) = 4 > 0, l(v4) = 2 и min(2, 4) = 2. Сток помечен. Переходим к операции Б - величения потока.
13. Сток имеет пометку (-v4, 2). Поэтому меньшаем поток вдоль дуги (v5, v4) на 2.
14. Вершина v4 имеет пометку (-v3, 2). Поэтому меньшаем поток вдоль дуги (v4, v3) на 2.
15. Вершина v3 имеет пометку (-v1, 2). Поэтому меньшаем поток вдоль дуги (v3, v1) на 2. Мы получили новый поток величины 6 (рис. 2.3). По теореме 1 этот максимальный. Проверим это.

Рис. 2.3. Максимальный поток
16. Стираем все пометки.
17. Присваиваем вершине v1 пометку (+, 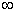 ).
).
18. Вершины, смежные вершине v1, нельзя помечать, поскольку дуга (v4, v3) насыщенна - φ(v1, v2) = φ(е1) = с(е1) = 6, через дугу (v3, v1) поток не передаётся. Сток остался не помеченным. Значит, полученный поток максимальный. Дуги (v1, v2) и (v3, v1) образуют минимальный разрез. Множество помеченных вершин образует ту его сторону, которая содержит источник: Vs = {v1}. Непомеченные вершины образуют другую сторону разреза, который содержит сток: Vt = { v2, v3, v4, v5}. Построенный поток имеет вид φ(е1) = 6, φ(е5) = 8, φ(е6) = 2, φ(е4) = 2, φ(е3) = 2, φ(е2) = φ(е7) = 0.
2.5. Графы со многими источниками и стоками
лгоритм Форда-Фалкерсона примененный и для определения величины максимального потока между множеством вершин - источников и множествома вершин - стоков. Разобьем множество вершин на множество источников V+ = {v  аV: Q(v) > 0}, которые образуют поток,
множество стоков V- = {v
аV: Q(v) > 0}, которые образуют поток,
множество стоков V- = {v  аV: Q(v) < 0}, которые используют поток и множество промежуточных вершин V0 = {v
аV: Q(v) < 0}, которые используют поток и множество промежуточных вершин V0 = {v  аV: Q(v) = 0}, которые сохраняют поток
аV: Q(v) = 0}, которые сохраняют поток  . Преобразуем поток φ в поток, который имеет только один источник и только один сток, величив количество вершин в сети. Для этого добавим две новые вершины - фиктивный источник vs и фиктивный сток vt. Соединим вершину vs со всеми действительными источниками.
Этим дугам припишем поток, который образован соответствующим источником. А из каждого действительного стока направим дугу в фиктивный сток vt. Этим дугам припишем поток, который используется соответствующим стоком. При этом пропускные способности добавленных дуг считаем бесконечными. В результате получаем сеть с одним источником и одним стоком. Применяя к ней алгоритм Форда-Фалкерсона, находим максимальный поток,
который максимальный и для исходной сети.
. Преобразуем поток φ в поток, который имеет только один источник и только один сток, величив количество вершин в сети. Для этого добавим две новые вершины - фиктивный источник vs и фиктивный сток vt. Соединим вершину vs со всеми действительными источниками.
Этим дугам припишем поток, который образован соответствующим источником. А из каждого действительного стока направим дугу в фиктивный сток vt. Этим дугам припишем поток, который используется соответствующим стоком. При этом пропускные способности добавленных дуг считаем бесконечными. В результате получаем сеть с одним источником и одним стоком. Применяя к ней алгоритм Форда-Фалкерсона, находим максимальный поток,
который максимальный и для исходной сети.
Проиллюстирируем на примере преобразования сети с несколькими источниками и несколькими стоками до сети с одним источником и одним стоком.

Рис. 2.4. Сеть с двумя стоками
На рис. 2.4 изображена сеть с двумя источниками v1 и v3 и тремя стоками v7, v8, v9 Q (v1) = 5, Q (v3) = 3, Q (v7) = 3, Q (v8) = 4, Q (v9) = 1, Q (v2) = Q (v4) = Q (v5) = Q (v6) = 0
Преобразуем эту сеть в сеть с одним источником и одним стоком.
На рис. 2.5 изображена сеть же с одним источником vs и одним стоком vt.

Рис. 2.5. Преобразованная сеть
2.6. Задача о многополюсном максимальном потоке
Рассмотрим задачу нахождения максимального потока для всех пар злов в неориентированной сети. Эту задачу можно рассматривать как обобщение задачи с одним источником и одним стоком, которую можно решить, применяя алгоритм Форда-Фалкерсона для каждой пары вершин. Однако более эффективным является алгоритм, предложенный Р. Гомори и Т. Ху.
лгоритм Гомори-Ху
1. Выберем некоторые две вершины графа. Обозначим одну из них через vs, а другую через vt.
2. Применим алгоритм Форда-Фалкерсона и найдём максимальный поток из источника vs в сток vt. При этом множество помеченных вершин и множество непомеченных вершин образуют две стороны минимального разреза Vs и Vt.
3. Выберем две вершины графа vi и vj  аVs.
аVs.
4. Заменим дуги из минимального разреза (Vs, Vt) одной дугой, вершины бока разреза, в котором не лежат вершины vi , vj, (например, Vt), - одной вершиной. Пропускную способность в таким образом определённой дуге примем равной пропускной способности разреза (Vs, Vt).
5. Положим: vi = vs,
vj = vt и вернемся ко второму шагу. После того, как будет выбрана n - 1 пара вершин, мы определим все 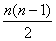 авеличин максимального потока для исходной сети. Основная идея алгоритма лежит в итеративном построении максимального остовного дерева, ветви которого соответствуют разрезам, а пропускные возможности ветвей равны пропускным способностям этих разрезов. Если бы мы применили алгоритм Форда-Фалкерсона к каждой паре вершин, то нам бы пришлось его применить
авеличин максимального потока для исходной сети. Основная идея алгоритма лежит в итеративном построении максимального остовного дерева, ветви которого соответствуют разрезам, а пропускные возможности ветвей равны пропускным способностям этих разрезов. Если бы мы применили алгоритм Форда-Фалкерсона к каждой паре вершин, то нам бы пришлось его применить 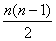 араз. В алгоритме же Гомори-Ху максимальный поток между парой вершин определяется с помощью алгоритма расстановки пометок только n - 1 раз. Проиллюстрируем на примере алгоритм Гомори-Ху.
араз. В алгоритме же Гомори-Ху максимальный поток между парой вершин определяется с помощью алгоритма расстановки пометок только n - 1 раз. Проиллюстрируем на примере алгоритм Гомори-Ху.
Рассмотрим сеть, изображённую на рис. 2.6.

Рис. 2.6. Сеть с пропускными возможностями
Числа, приписанные дугам, отвечают их пропускным способностям, отвечают их пропускным способностям. Нужно для каждой пары злов сети определить величину максимального потока между ними. Эта задача решается при n - 1= 6 - 1 = 5 итераций алгоритма Гомори-Ху. Если алгоритм Форда-Фалкерсона расстановки пометок применялся бы к каждой паре злов, то нужно было бы решить пятнадцать задач о максимальном потоке.
Реализуем алгоритм Гомори-Ху на данной сети.
1. Выберем вершины s = v1 и t = v2. Минимальную пропускную способность относительно источника s = v1 и стока t = v2 имеет разрез со сторонами Vs = {v1, v3, v4, v5, v6} и Vt = {v2}. По теореме 1 величина максимального потока между вершинами v1 и v2 равна пропускной способности разреза (Vs, Vt): w12 = w21 = c(Vs, Vt) = 2 + 3 = 5. Объединим вершины с Vs в одну вершину и соединим её с вершиной v2 веткой с пропускной способностью 5 (рис. 2.7).

Рис. 2.7. Первый шаг алгоритма
2. Выберем вершины s = v1 и t = v3. Минимальную пропускную способность относительно источника s = v1 и стока t = v3 имеет разрез со сторонами Vs = {v1} и Vt = {v2, v3, v4, v5, v6}. По теореме 1 величина максимального потока между вершинами v1 и v3 равна пропускной способности разреза (Vs, Vt): w13 = w31 = c(Vs, Vt) = 2 + 4 + 2 = 8. Объединим вершины v3, v4, v5, v6 в одну вершину и соединим её с вершиной v1 веткой с пропускной способностью 8 (рис. 2.8).

Рис 2.8. Второй шаг
3. Выберем вершины s = v4 и t = v3. Минимальную пропускную способность относительно источника s = v4 и стока t = v3 имеет разрез со сторонами Vs = {v4} и Vt = {v1, v2, v3, v5, v6}. По теореме 1 авеличина максимального потока между вершинами v4 и v3 равна пропускной способности разреза (Vs, Vt): w43 = w34 = c(Vs, Vt) = 2 + 5 + 4 = 11. Объединим вершины v3, v5, v6 в одну вершину и соединим её с вершиной v4 веткой с пропускной способностью 11 (рис. 2.9).

Рис. 2.9. Третий шаг
4. Выберем вершины s = v5 и t = v3. Минимальную пропускную способность относительно источника s = v5 и стока t = v3 имеет разрез со сторонами Vs = {v5} и Vt = {v1, v2, v3, v4, v6}. Величина максимального потока между вершинами v5 и v3 равна пропускной способности разреза (Vs, Vt): w53 = w35 = c(Vs, Vt) = 5 + 4 = 9. Объединим вершины v3, v6 в одну вершину и соединим её с вершиной v5 веткой с пропускной способностью 9 (рис. 2.10).

Рис. 2.10. Четвёртый шаг
5. Выберем вершины s = v6 и t = v3. Минимальную пропускную способность относительно источника s = v6 и стока t = v3 имеет разрез со сторонами Vs = {v6} и Vt = {v1, v2, v3, v4, v5}.

Рис. 2.11. Остаточное дерево разрезов
Величина максимального потока между вершинами v6 и v3 равна пропускной способности разреза (Vs, Vt): w63 = w36 = c(Vs, Vt) = 5 + 6 + 4 = 15. Объединим вершину v3 с вершиной v6 веткой с пропускной способностью 15 (рис. 2.11).
По дереву перерезов, изображённого на рис. 2.11, легко найти остальные величины максимальных потоков. Например, v16 = v61 = 8, поскольку в цепи дерева разрезов, которая соединяет вершины v1 и v2, минимальная пропускная способность веток равна 8. Запишем величины максимальных потоков в виде матрицы:
 .
.
Здесь на пересечение i-строки и j-столбца стоит величина максимального потока между вершинами vi и vj.
3.3. Реализация программы
Сравним результаты вычислений с помощью программы и вручную. Для ручного способа вычислений будем использовать алгоритм Форда-Фалкерсона.
1. Возьмём поток, изображённый на рисунке 3.8 как начальный допустимый поток. Он имеет величину 3.
2. Присвоим источнику, вершине v1, пометку (+, ∞). Вершина v1 помечена, но не просмотрена.
3. Просмотрим вершины, смежные с вершиной v1. Вершине v2 присвоим пометку (+v1, 1), вершине v3 - пометку (+v1, 1),т.к. φ(v1, v2) = 2 < 3 = с1, φ(v1, v3) = 1 < 2 = с2. Вершина v1 помечена и просмотрена, вершины v2 и v3 помечены, но не просмотрены.

Рис. 3.8. Поток величины 3
4. Просмотрим вершины, смежные с вершиной v2. Из вершин, смежных с вершиной v2, не помечена только вершина v4. Вершине v4 присваиваем пометку (+v2, 1), поскольку φ(v2, v4) = 1 < 3 = с3.
5. Просмотрим вершины, смежные с вершиной v3. Из вершин, смежных с вершиной v3, не помечена только вершина v5. Вершине v5 присваиваем пометку (+v3, 1), поскольку φ(v3, v5) = 2 < 4 = с4.
6. Просмотрим вершины, смежные с вершиной v4. Смежной и непомеченной является вершина v6. Присваиваем ей пометку (+v4, 1), поскольку φ(v4, v6) = 1 < 4 = с5.
7. Просмотрим вершины, смежные с вершиной v5. Смежной и непомеченной является вершина v7. Присваиваем ей пометку (+v5, 1), поскольку φ(v5, v7) = 2 < 3 = с6.
8. Просмотрим вершины, смежные с вершиной v6. Смежной и непомеченной является вершина v8. Присваиваем ей пометку (+v6, 1), поскольку φ(v6, v8) = 2 < 5 = с7. Сток помечен. Переходим к операции Б - величению потока.
9. Сток имеет пометку (+v6, 1). Поэтому величиваем поток по дуге (v6, v8) на 1.
10. Вершина v6 имеет пометку (+v4, 1). Поэтому величиваем поток по дуге (v4, v6) на 1.
11.. Вершина v4 имеет пометку (+v2, 1). Поэтому величиваем поток по дуге (v2, v4) на 1.
12.. Вершина v2 имеет пометку (+v1, 1). Поэтому величиваем поток по дуге (v1, v2) на 1. Мы получили новый поток величины 4 (рис. 3.9).

Рис. 3.9. Поток величины 4
13. Стираем все пометки.
14. Присваиваем вершине v1 пометку (+, ∞).
15. Просмотрим вершины, смежные с вершиной v1. Вершину v2 не помечаем, поскольку φ(v1, v2) = 3 = c(e1), вершине v3 присваиваем пометку (+v1, 1).
16. Просмотрим вершины, смежные с вершиной v3. Вершине v2 присваиваем пометку (-v3, 1), поскольку φ(v2, v3) = 1 > 0, l(v) = 1 и min(1, 1) = 1, вершине v5а припишем пометку (+v3, 1), так как φ(v3, v5) = 2 < 4 = c8.
17. Просмотрим вершины, смежные с вершиной v4. Вершине v6 присваиваем пометку (+v4, 1), поскольку φ(v4, v6) = 3 < 5 = с9.
18. Просмотрим вершины, смежные с вершиной v5. Вершине v7 присваиваем пометку (+v5, 1), поскольку φ(v5, v7) = 2 < 3 = с10.
19. Просмотрим вершины, смежные с вершиной v6. Вершине v8 присваиваем пометку (+v6, 1), поскольку φ(v6, v8) = 3 < 5 = с11. Сток помечен. Переходим к операции Б - величению потока.
20. Сток имеет пометку (+v6, 1). Поэтому величиваем поток по дуге (v6, v8) на 1.
21. Вершина v6 имеет пометку (+v4, 1). Поэтому величиваем поток по дуге (v4, v6) на 1.
22. Вершина v4 имеет пометку (+v2, 1). Поэтому величиваем поток по дуге (v2, v4) на 1.
23. Вершина v2 имеет пометку (-v3, 1). Поэтому меньшаем поток по дуге (v2, v3) на 1.
24. Вершина v3 имеет пометку (+v1, 1). Поэтому величиваем поток по дуге (v1, v3) на 1. Получили новый поток величины 5 (рис. 3.10).

Рис. 3.10. Поток величины 5
25. Стираем все пометки.
26. Присваиваем вершине v1 пометку (+, ∞).
27. Вершины, смежные вершине v1, нельзя пометить, поскольку дуга (v1, v2) насыщена - φ(v1, v2) = φ(е1) = с(е1) = 3, и дуга (v1, v3) тоже насыщена - φ(v1, v3) = φ(е2) = с(е2) = 2. Сток остался непомеченным. Значит, полученный поток максимален.
теперь найдём максимальный поток с помощью программы. Для этого введём матрицу пропускных способностей в соответствующие поля программы. Матрица имеет следующий вид:

Результат вычислений оказался тем же. Мы получили максимальный поток величины 5 (рис. 3.11).

Рис. 3.11.
3.4. Описание программного кода
Прикладная программа Max_potоk написана языком Object Pascal в интегрированной среде Delphi7.
Окно программы (Form1: TForm) содержит такие компоненты:
- текстовые поля (Eij: TEdit ; Inij: TEdit (i,j = 1..10));
Ц компоненты (STy: TStaticText (y = 1..10), OSTx: TStaticText (x = 1..10), VSTz: TStaticText (z = 1..10), OVSTe: TStaticText (e = 1..10), StaticTextij: TStaticText (i = 4, j = 1..4));
- надписи (Label1, Label2, Label3: TLabel);
- панель группировки компонентов (GB1: TGroupBox);
- кнопки (Buttonk: TButton (k = 1..5)).
В программе отслеживается 7 действий (табл. 6).
Таблица 6
|
Название действия |
Назначение |
|
TButton1.Click |
Рассчитывает максимальный поток |
|
TButton2.Click |
Создаёт таблицы матриц пропускных способностей и потока заданной размерности |
|
TButton3.Click |
Считает одну итерацию |
|
TButton4.Click |
Выводит пометки |
|
TButton5.Click |
Начинает итерацию заново |
|
TForm1.Create |
Задаёт высоту и ширину окна программы |
|
TForm1.Close |
Совершает затухание формы при её закрытии |
Предназначение текстовых полей приведено в таблице 7.
|
Метка поля |
Название поля |
Предназначение |
|
Количество |
Col |
Задаётся количество вершин сети |
|
s= |
|
Задаётся источник сети |
|
t= |
|
Задаётся сток сети |
|
Вершина |
р1 |
Задаётся вершина, пометки которой будут рассчитываться |
|
Предыдущая вершина |
р2 |
Выводятся пометки вершины |
|
Знак |
р3 |
|
|
d |
р4 |
|
|
Максимальный поток |
max |
Выводится максимальный поток сети |
|
Xij |
Inij |
Задаётся матрица пропускных способностей сети |
|
Xij |
Eij |
Выводится матрица потока в сети |
Таблица 7
ВЫВОДЫ
Решая жизненные практические задачи, мы неоднократно сталкиваемся с проблемой поиска максимальных потоков в сетях (поиск максимального потока машин в сети дорог без возникновения пробок, поиск максимального количества нефти, которую можно перекачать по трубопроводу и др.).
В данной работе изучалась эта проблема, была рассмотрена теория, которая изучает методы поиска максимальных потоков в сетях, изучен алгоритм поиска максимального потока (алгоритм Форда-Фалкерсона), в интегрированной среде Delphi было разработано дополнение, которое позволяет в добной для пользователя форме найти максимальный поток в заданной сети.
Это дополнение может быть использовано при проведении практических занятий по теме Теория графов для студентов специальностей Математика и Информатика при изучении дисциплины Дискретная математика, также для проверки тестовых заданий по этой теме.
ЛИТЕРАТУРА
1. Алгоритмы и программы решения задач на графах и сетях. Отв. ред. М.И. Нечепуренко. - Новосибирск: Наука. Сиб. отделение, 1990. - 513 с.
2. Андрйчук В.
., Комарницький М.Я.,
щук Ю.Б. Вступ до дискретно
3. Архангельский А.Я. Приемы программирования в Delphi. Версии 5 Ц 7. М.: ЗАО Издательство БИНОМ, 2003.
4. Дискретна математика: Пдручник/ Ю.М. Бардачов, Н.А. Соколова, В.к. Ходаков; за ред. В.к. Ходакова. - К.: Вища шк., 2002. - 287 с.: л.
5. Дискретная математика: логика, группы, графы/ О.Е. Акимов. - 2-е изд., доп. - М.: Лаборатория Базовых Знаний, 2003. - 376 с.: ил.
6. Зыков А.А. Основы теории графов. - М.: Наука, 1987. - 381 с.
7. Климова Л.М. Delphi 7. Основы программирования. Решение типовых задач. Самоучитель - М.: КУДИЦ-ОБРАЗ, 2004. - 480 с.
8. Крстофдес Р. Теория графов. Переклад на росйську мову Мир 1978.
9. Лекции по дискретной математике/ Ю.В. Капитонова, С.Л. Кривой, А.А. Летичевский и др. - Пб.: БХВ-Петербург, 2004. - 624 с.
10. Лекции по теории графов/ Емеличев В.А., Мельниченков О.И., Сарванов В.И., Тышкевич Р.И. - М.: Наука, Гл. ред. физ.-мат. лит., 1990. - 384 с.
11. Лекции по теории графов: учебн. пособие. Ц М.: Наука, 1990. - 384 с.
12. Липский В. Комбинаторика для программистов: Пер. с польск. - М.: Мир, 1988. - 213 с.: ил.
13. Магрупов Т.М. Графы, сети, алгоритмы и их приложения/ Под ред. Ф.Б. Абуталиева; АН УР, Ин-т кибернетики с ВЦ зНПО Кибернетика: - Ташкент: Фан, 1990. - 120 с.
14. Математическое программирование (с элементами информационных технологий): учеб. пособие для студ. нематемат. спец. вузов/ В.Р. Кулян, Е.А. Юнькова, А.Б. Жильцов. - К.: МАУП, 2. - 124 с.: ил.
15. Мiхайленко В.М. Дискретна математика. - К.: квропейський н-т, 2003. - 319.
16. Новиков Ф.А. Дискретная математика для программистов. - Пб.: Питер, 2004. - 302 с.: ил.
17. Седжвк Д. Програмирование на С++. Часть 5. Алгоритмы на графах. Ки
18. Теория графов и её применение: сборник научных трудов/ Институт математики им. С.Л. Соболева. - Новосибирск, 1996. - 106 с.
19. Яблонский С.В. Введение в дискретную митематику. - М.: Наука, 1986. - 384 с.
ПРИЛОЖЕНИЕ
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, Grids, DBGrids, AxCtrls, OleCtrls, VCF1, ComCtrls, StdCtrls;
type
TForm1 = class(TForm)
E11: TEdit; E21: TEdit; E31: TEdit; E41: TEdit; E51: TEdit; E61: TEdit;
E71: TEdit; E81: TEdit; E91: TEdit; E101: TEdit; E12: TEdit; E22: TEdit;
E32: TEdit; E42: TEdit; E52: TEdit; E62: TEdit; E72: TEdit; E82: TEdit;
E92: TEdit; E102: TEdit; E13: TEdit; E23: TEdit; E33: TEdit; E43: TEdit;
E53: TEdit; E63: TEdit; E73: TEdit; E83: TEdit; E93: TEdit; E103: TEdit;
E14: TEdit; E24: TEdit; E34: TEdit; E44: TEdit; E54: TEdit; E64: TEdit;
E74: TEdit; E84: TEdit; E94: TEdit; E104: TEdit; E15: TEdit; E25: TEdit;
E35: TEdit; E45: TEdit; E55: TEdit; E65: TEdit; E75: TEdit; E85: TEdit;
E95: TEdit; E105: TEdit; E16: TEdit; E26: TEdit; E36: TEdit; E46: TEdit;
E56: TEdit; E66: TEdit; E76: TEdit; E86: TEdit; E96: TEdit; E106: TEdit;
E17: TEdit; E27: TEdit; E37: TEdit; E47: TEdit; E57: TEdit; E67: TEdit;
E77: TEdit; E87: TEdit; E97: TEdit; E107: TEdit; E18: TEdit; E28: TEdit;
E38: TEdit; E48: TEdit; E58: TEdit; E68: TEdit; E78: TEdit; E88: TEdit;
E98: TEdit; E108: TEdit; E19: TEdit; E29: TEdit; E39: TEdit; E49: TEdit;
E59: TEdit; E69: TEdit; E79: TEdit; E89: TEdit; E99: TEdit; E109: TEdit;
E110: TEdit; E210: TEdit; E310: TEdit; E410: TEdit; E510: TEdit;
E610: TEdit; E710: TEdit; E810: TEdit; E910: TEdit; E1010: TEdit;
In11: TEdit; In21: TEdit; In31: TEdit; In41: TEdit; In51: TEdit;
In61: TEdit; In71: TEdit; In81: TEdit; In91: TEdit; In101: TEdit;
In12: TEdit; In22: TEdit; In32: TEdit; In42: TEdit; In52: TEdit;
In62: TEdit; In72: TEdit; In82: TEdit; In92: TEdit; In102: TEdit;
In13: TEdit; In23: TEdit; In33: TEdit; In43: TEdit; In53: TEdit;
In63: TEdit; In73: TEdit; In83: TEdit; In93: TEdit; In103: TEdit;
In14: TEdit; In24: TEdit; In34: TEdit; In44: TEdit; In54: TEdit;
In64: TEdit; In74: TEdit; In84: TEdit; In94: TEdit; In104: TEdit;
In15: TEdit; In25: TEdit; In35: TEdit; In45: TEdit; In55: TEdit;
In65: TEdit; In75: TEdit; In85: TEdit; In95: TEdit; In105: TEdit;
In16: TEdit; In26: TEdit; In36: TEdit; In46: TEdit; In56: TEdit;
In66: TEdit; In76: TEdit; In86: TEdit; In96: TEdit; In106: TEdit;
In17: TEdit; In27: TEdit; In37: TEdit; In47: TEdit; In57: TEdit;
In67: TEdit; In77: TEdit; In87: TEdit; In97: TEdit; In107: TEdit;
In18: TEdit; In28: TEdit; In38: TEdit; In48: TEdit; In58: TEdit;
In68: TEdit; In78: TEdit; In88: TEdit; In98: TEdit; In108: TEdit;
In19: TEdit; In29: TEdit; In39: TEdit; In49: TEdit; In59: TEdit;
In69: TEdit; In79: TEdit; In89: TEdit; In99: TEdit; In109: TEdit;
In110: TEdit; In210: TEdit; In310: TEdit; In410: TEdit; In510: TEdit;
In610: TEdit; In710: TEdit; In810: TEdit; In910: TEdit; In1010: TEdit;
ST1: TStaticText; ST2: TStaticText; ST3: TStaticText; ST4: TStaticText;
ST5: TStaticText; ST6: TStaticText; ST7: TStaticText; ST8: TStaticText;
ST9: TStaticText; ST10: TStaticText; OST1: TStaticText;
OST4: TStaticText; OST3: TStaticText; OST2: TStaticText;
OST5: TStaticText; OST6: TStaticText; OST7: TStaticText;
OST8: TStaticText; OST9: TStaticText; OST10: TStaticText;
VST1: TStaticText; VST2: TStaticText; VST3: TStaticText;
VST4: TStaticText; VST5: TStaticText; VST6: TStaticText;
VST7: TStaticText; VST8: TStaticText; VST9: TStaticText;
VST10: TStaticText; OVST1: TStaticText; OVST2: TStaticText;
OVST3: TStaticText; OVST4: TStaticText; OVST5: TStaticText;
OVST6: TStaticText; OVST7: TStaticText; OVST8: TStaticText;
OVST9: TStaticText; OVST10: TStaticText; : TEdit;
StaticText41: TStaticText; : TEdit; StaticText42: TStaticText;
Button1: TButton; StaticText43: TStaticText; StaticText44: TStaticText;
col: TEdit; label1: TLabel; Button2: TButton; Label2: TLabel;
max: TEdit; Button3: TButton; GB1: TGroupBox; Label3: TLabel;
Label4: TLabel; Label5: TLabel; Label6: TLabel; p1: TEdit;
p2: TEdit; p3: TEdit; p4: TEdit; Button4: TButton; Button5: TButton;
procedure Button1Click(Sender: TObject);
procedure Button2Click(Sender: TObject);
procedure FormClose(Sender: TObject; var Action: TCloseAction);
procedure FormCreate(Sender: TObject);
procedure Button3Click(Sender: TObject);
procedure Button4Click(Sender: TObject);
procedure Button5Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
function min(x,y: double): double;
const p1=10;
type
sign=(minus,plus);
ibool=0..1;
Rec=record
s:sign; {направление дуги}
n:1..p1; {предшествующая вершина в аугментальной цепи}
delta:double; {величина возможного величения потока}
end;
var
Form1: TForm1;
F: array of array of double;
P: array of Rec;
implementation
{$R *.dfm}
function min(x,y: double): double;
begin
if x < y then
Result := x
else
Result := y;
end;
procedure TForm1.Button1Click(Sender: TObject);
label M;
const p1=10;
type
sign=(minus,plus);
ibool=0..1;
Rec=record
s:sign; {направление дуги}
n:1..p1; {предшествующая вершина в аугментальной цепи}
delta:double; {величина возможного величения потока}
end;
var i,j: integer;
del,ch:double;
C,F: array of array of double;
P: array of Rec;
N,S: array of ibool;
a:ibool;
pp,s1,t1,x: byte;
input,output:array of array of TEdit;
begin
pp:=StrToInt(col.Text);
SetLength(input,pp);
SetLength(output,pp);
SetLength(C,pp);
SetLength(F,pp);
SetLength(P,pp);
SetLength(N,pp);
SetLength(S,pp);
for i:=0 to pp-1 do
begin
SetLength(input[i],pp);
SetLength(output[i],pp);
SetLength(C[i],pp);
SetLength(F[i],pp);
end;
for i:=1 to pp do
for j:=1 to pp do
begin
F[i-1,j-1] := 0; {вначале поток нулевой}
input[i-1,j-1]:=FindComponent(Format('In%d%d',[i,j])) as TEdit;
output[i-1,j-1]:=FindComponent(Format('E%d%d',[i,j])) as TEdit;
if input[i-1,j-1].Text<>'' then C[i-1,j-1]:=StrToFloat(input[i-1,j-1].Text)
else C[i-1,j-1]:=0;
end;
s1 := StrToInt(.Text[2]);
if (s1=1) and (length(.Text)=3) then
s1:=10;
t1 := StrToInt(.Text[2]);
if (t1=1) and (length(.Text)=3) then
t1:=10;
M: {итерация величения потока}
for i:=1 to pp do
begin
S[i-1] := 0;
N[i-1] := 0;
with P[i-1] do
begin
//s := null;
//n := nil;
delta := 0;
end;
end;
S[s1-1]:=1;
with P[s1-1] do
begin
s:=plus;
n:=s1;
end;
repeat
a:=0; {признак расширения S}
for i:=1 to pp do
begin
if (S[i-1]=1) and (N[i-1]=0) then
begin
for j:=1 to pp do
begin
if C[i-1,j-1]<>0 then
begin
if (S[j-1]=0) and (F[i-1,j-1] < C[i-1,j-1]) then
begin
S[j-1] := 1;
with P[j-1] do
begin
s := plus;
n := i;
if i=s1 then delta := C[i-1,j-1] - F[i-1,j-1]
else delta := min(P[i-1].delta,C[i-1,j-1] - F[i-1,j-1]);
end;
a := 1;
аend;
end;
if C[j-1,i-1]<>0 then
begin
if (S[j-1]=0) and (F[j-1,i-1]>0) then
begin
S[j-1] := 1;
with P[j-1] do
begin
s := minus;
n := i;
if i=s1 then delta := F[j-1,i-1]
else delta := min(P[i-1].delta,F[j-1,i-1]);
end;
a:=1;
end;
end;
end;
N[i-1] := 1;
end;
end;
if S[t1-1]<>0 then
begin
x:=t1;
del:=P[t1-1].delta;
while x<>s1 do
begin
if P[x-1].s=plus then
F[P[x-1].n-1,x-1]:=F[P[x-1].n-1,x-1]+del
else
F[x-1,P[x-1].n-1]:=F[x-1,P[x-1].n-1]-del;
x:=P[x-1].n
end;
goto M;
end;
until a=0;
ch:=0;
for i:=1 to pp do
begin
ch:=ch+F[s1-1,i-1];
for j:=1 to pp do
begin
if C[i-1,j-1]<>0 then
output[i-1,j-1].Text := FloatToStr(F[i-1,j-1])
else
output[i-1,j-1].Text := '';
end;
end;
max.Text := FloatToStr(ch);
end;
//----------------------------------------------------
procedure TForm1.Button2Click(Sender: TObject);
const p1=10;
var InG,InV,OutG,OutV :array[1..p1] of TStaticText;
i,pp,j: byte;
input,output:array[1..p1,1..p1] of TEdit;
begin
.Text:='';
.Text:='';
max.Text:='';
pp:=StrToInt(Col.Text);
SetLength(F,pp);
for i:=1 to pp do
begin
SetLength(F[i-1],pp);
for j:=1 to pp do
F[i-1,j-1] := 0;
end;
for i:=1 to p1 do
begin
InG[i] := FindComponent(Format('ST%d',[i])) as TStaticText;
InV[i] := FindComponent(Format('VST%d',[i])) as TStaticText;
OutG[i] := FindComponent(Format('OST%d',[i])) as TStaticText;
OutV[i] := FindComponent(Format('OVST%d',[i])) as TStaticText;
if i<=pp then
begin
InG[i].Visible:=true;
InV[i].Visible:=true;
OutG[i].Visible:=true;
OutV[i].Visible:=true;
end
else
begin
InG[i].Visible:=false;
InV[i].Visible:=false;
OutG[i].Visible:=false;
OutV[i].Visible:=false;
end;
for j:=1 to p1 do
begin
input[i,j] := FindComponent(Format('In%d%d',[i,j])) as TEdit;
output[i,j] := FindComponent(Format('E%d%d',[i,j])) as TEdit;
if (i<=pp) and (j<=pp) then
begin
input[i,j].Visible:=true;
output[i,j].Visible:=true;
input[i,j].Text:='';
output[i,j].Text:='';
end
else
begin
input[i,j].Visible:=false;
output[i,j].Visible:=false;
end;
end;
end;
end;
procedure TForm1.FormClose(Sender: TObject; var Action: TCloseAction);
var
i, cavb : 0..255;
begin
if AlphaBlend=False then
begin
AlphaBlendValue:=255;
AlphaBlend:=True;
end;
cavb:=AlphaBlendValue;
for i := cavb downto 0 do
begin
AlphaBlendValue := i;
Application.ProcessMessages;
end
end;
procedure TForm1.FormCreate(Sender: TObject);
begin
Form1.Height:=600;
Form1.Width:=800;
end;
procedure TForm1.Button3Click(Sender: TObject);
var i,j: integer;
del:double;
C: array of array of double;
N,S: array of ibool;
a:ibool;
pp,s1,t1,x: byte;
input,output:array of array of TEdit;
begin
p1.Text :='';
p2.Text :='';
p3.Text :='';
p4.Text :='';
pp:=StrToInt(col.Text);
SetLength(input,pp);
SetLength(output,pp);
SetLength(C,pp);
SetLength(P,pp);
SetLength(N,pp);
SetLength(S,pp);
for i:=0 to pp-1 do
begin
SetLength(input[i],pp);
SetLength(output[i],pp);
SetLength(C[i],pp);
end;
for i:=1 to pp do
for j:=1 to pp do
begin
input[i-1,j-1]:=FindComponent(Format('In%d%d',[i,j])) as TEdit;
output[i-1,j-1]:=FindComponent(Format('E%d%d',[i,j])) as TEdit;
if input[i-1,j-1].Text<>'' then C[i-1,j-1]:=StrToFloat(input[i-1,j-1].Text)
else C[i-1,j-1]:=0;
end;
s1 := StrToInt(.Text[2]);
if (s1=1) and (length(.Text)=3) then
s1:=10;
t1 := StrToInt(.Text[2]);
if (t1=1) and (length(.Text)=3) then
t1:=10;
for i:=1 to pp do
begin
S[i-1] := 0;
N[i-1] := 0;
with P[i-1] do
begin
//s := null;
//n := nil;
delta := 0;
end;
end;
S[s1-1]:=1;
with P[s1-1] do
begin
s:=plus;
n:=s1;
end;
repeat
a:=0; {признак расширения S}
for i:=1 to pp do
begin
if (S[i-1]=1) and (N[i-1]=0) then
begin
for j:=1 to pp do
begin
if C[i-1,j-1]<>0 then
begin
if (S[j-1]=0) and (F[i-1,j-1] < C[i-1,j-1]) then
begin
S[j-1] := 1;
with P[j-1] do
begin
s := plus;
n := i;
if i=s1 then delta := C[i-1,j-1] - F[i-1,j-1]
else delta := min(P[i-1].delta,C[i-1,j-1] - F[i-1,j-1]);
end;
a := 1;
end;
end;
if C[j-1,i-1]<>0 then
begin
if (S[j-1]=0) and (F[j-1,i-1]>0) then
begin
S[j-1] := 1;
with P[j-1] do
begin
s := minus;
n := i;
if i=s1 then delta := F[j-1,i-1]
else delta := min(P[i-1].delta,F[j-1,i-1]);
end;
a:=1;
end;
end;
end;
N[i-1] := 1;
end;
end;
if S[t1-1]<>0 then
begin
x:=t1;
del:=P[t1-1].delta;
while x<>s1 do
begin
if P[x-1].s=plus then
F[P[x-1].n-1,x-1]:=F[P[x-1].n-1,x-1]+del
else
F[x-1,P[x-1].n-1]:=F[x-1,P[x-1].n-1]-del;
x:=P[x-1].n
end;
Break;
end;
until a=0;
for i:=1 to pp do
begin
for j:=1 to pp do
begin
if C[i-1,j-1]<>0 then
output[i-1,j-1].Text := FloatToStr(F[i-1,j-1])
else
output[i-1,j-1].Text := '';
end;
end;
end;
procedure TForm1.Button4Click(Sender: TObject);
var s1,ver: byte; // Вершина
begin
p4.Font.Name := 'MS Sans Serif';
ver := StrToInt(p1.Text[2]);
if (ver=1) and (length(p1.Text)=3) then
ver:=10;
s1 := StrToInt(.Text[2]);
if (s1=1) and (length(.Text)=3) then
s1:=10;
if P[ver-1].s=plus then p3.Text := '+'
else p3.Text := '-';
p2.Text := 'x' + IntToStr(P[ver-1].n);
if ver<>s1 then
p4.Text := FloatToStr(P[ver-1].delta)
else
begin
p4.Font.Name :='Symbol';
p4.Text := 'е';
end;
end;
procedure TForm1.Button5Click(Sender: TObject);
var pp,i,j : integer;
output:array of array of TEdit;
begin
pp:=StrToInt(Col.Text);
SetLength(F,pp);
SetLength(output,pp);
for i:=1 to pp do
begin
SetLength(output[i-1],pp);
SetLength(F[i-1],pp);
for j:=1 to pp do
begin
F[i-1,j-1] := 0;
output[i-1,j-1]:=FindComponent(Format('E%d%d',[i,j])) as TEdit;
output[i-1,j-1].Text := '';
end;
end;
end;
end.


 Ц замкнутый
отрезок.
Ц замкнутый
отрезок.